π型连接件对冷弯薄壁拼合梁抗弯性能影响分析

【摘 要】 为研究Π型连接件对由冷弯薄壁C型截面钢拼合得到的钢梁在受弯情况下的力学性能的影响，文章利用有限元软件ABAQUS对11根拼合梁建立精细有限元模型。对考虑初始缺陷的两端简支拼合梁进行两点加载，采用非线性分析方法对包含不同间距、长度、位置的Π型连接件的拼合梁有限元模型进行了数值参数分析，结果表明设置连接件能在一定程度上提高梁的抗弯承载力;减小Π型连接件的间距及增加连接件长度对梁的极限承载力提高作用并不显著;在纯弯段集中布置连接件可以很好的控制由局部屈曲现象的发生。

【关键词】冷弯薄壁组合梁; C型钢; Π型连接件; 抗弯承载力; 初始缺陷; ABAQUS

近年来，随着我国建筑工业化的推进，冷弯薄壁钢构件在低层和中层住宅及工业建筑的应用逐渐增长，同时冷弯薄壁拼合构件也应运而生。此类构件常通过螺栓、连接件等将简单形式截面的冷弯薄壁构件组合而成，通过此种方式，达到改变截面惯性矩增大截面面积的目的。目前规范对此类组合梁构件的设计的指导较少，国内外学者对冷弯薄壁拼合钢构件进行了大量研究。周绪红教授[1-3]采用试验和有限元方法分析了材料强度、翼缘宽厚比、腹板高厚比、板件厚度以及梁长度对冷弯薄壁卷邊槽钢组合工字梁的受弯性能的影响，并提出了计算冷弯薄壁卷边槽钢组合工字梁极限承载力的有效宽度法和折减强度法。赵阳[4]等通过试验及有限元软件研究了螺钉间距对冷弯薄壁型钢拼合箱形截面短柱承载力的影响。聂少锋[5]等通过有限元方法研究双肢开孔冷弯薄壁型钢拼合箱形截面立柱的轴向受力性能，对立柱长细比、腹板宽度、试件厚度、开洞情况及孔洞间距等参数的影响进行了非线性分析，并与规范对比提出了相应轴压承载力计算的建议修正公式。YoungB[6-7]等对不同腹板加劲尺寸的冷弯薄壁双肢背靠背拼合截面立柱进行了试验及有限元分析，并根据直接强度法计算试件最大承载力，对比实验结果，修正计算方法。通过实验验证方法的可靠性。Wang和Young [8]通过试验研究，给出了开放式和封闭式冷弯薄壁拼合梁的设计指导意见。

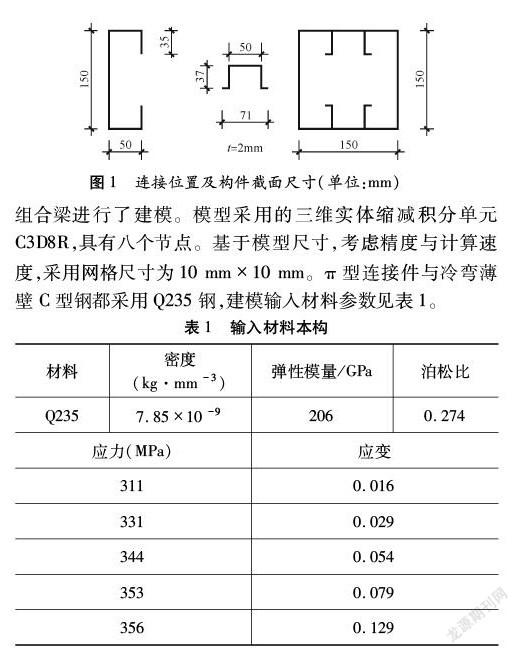
本文对由C型截面组成的冷弯薄壁拼合梁受弯性能进行了数值研究，该种拼合梁通过π型连接件将两根C型截面构件连接在一起形成组合梁，拥有双轴对称，具有更大的扭转刚度的优点。利用通用有限元软件ABAQUS [9]建立非线性有限元模型进行参数分析，研究了设置不同间距、长度、位置的Π型连接件对拼合梁强轴受弯情况下力学性能的影响。建立了11根拼合梁模型，模型两端简支，采用两点加载方式，连接件连接位置及构件截面尺寸如图1所示。

1 有限元分析

1.1 模型网格与材料

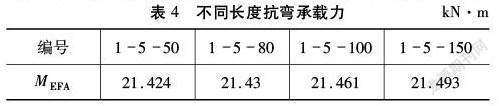
利用ABAQUS对9根不同π型连接件设置的冷弯薄壁组合梁进行了建模。模型采用的三维实体缩减积分单元C3D8R，具有八个节点。基于模型尺寸，考虑精度与计算速度，采用网格尺寸为10 mm×10 mm。π型连接件与冷弯薄壁C型钢都采用Q235钢，建模输入材料参数见表1。

1.2 接触与连接

建立垫块用以加载传递板及作为两端支座，垫块与试件为罚函数接触方法，考虑摩擦系数为0.3。为防止模型分析时发生穿透现象，建立硬解触。使用ABAQUS中的Tie约束模拟螺栓对连接件和C型钢的连接作用。

1.3 载荷和边界条件

分别在载荷传递板和试件之间的接触表面中间建立两个参考点，以模拟两个加载点。参考点采用Coupling在所有自由度上以运动学方式与相关节点耦合。同样建立两个端部耦合约束，参考点位于截面的质心处约束试件面外位移。对两端垫块固定实现试件的简支边界条件，通过对加载点位移控制进行加载。模型加载如图2所示。

工程结构肖姝玮： π型连接件对冷弯薄壁拼合梁抗弯性能影响分析

1.4 几何缺陷

在有限元模型中，对构件赋予了初始缺陷。通过在从ABAQUS中Linear perturbation下的Buckle分析步中计算，获得弹性临界屈曲分析获得的第一特征值屈曲模态，将局部几何缺陷导入到模型中，进行采用Risk分析步进行位移加载。对于初始缺陷的振幅，周绪红等[10]曾对冷弯薄壁C型钢构件局部初始缺陷进行实测，最大值为腹板高度的0.005倍，国外学者Schafer和Pekz[11]对两种不同类型的冷弯薄壁构件给出了对应概率的建议值，对应于50 %概率，局部几何缺陷振幅为0.34 t，其中t是构件厚度，综合考量本文有限元参数模型中采用几何缺陷振幅为0.68 mm。图3显示了从编号为1-5-50试件模型屈曲分析中获得的几何缺陷。

2 参数分析

为研究π型连接件不同设置方式对拼合梁抗弯性能的影响，考虑了连接件不同设置间距、连接件不同长度及梁通长布置与仅在纯弯段集中布置两种情况，同时建立不含有π型连接件的双肢冷弯薄壁C型拼合钢梁，编号为1-0-0试件作为对照。对拼合梁进行标记，各试件具体参数见表2。所有梁试件的模型长度为2 400 mm，弯矩跨度为1 000 mm。参数有限元分析结果以弯矩承载力和变形结果给出。

3 结果分析

3.1 π型连接件间距对组合梁抗弯性能影响

从有限元分析结果可以得到，组合梁在跨中位移30～40 mm左右时达到极限抗弯承载力，随着加载的进行，由于几何缺陷的存在，试件都将发生不同程度的屈曲破坏，如图4（a）、4（c）所示，设置连接件的组合梁抗弯承载力都大于未设置的参照组。由表3数据可以看出，随着π型连接件间距的减小，组合梁的抗弯承载能力呈现增涨趋势，见表3，但提高的抗弯承载力都相对较小。

3.2 π型连接件长度对组合梁抗性能影响

该组间距均为570 mm，连接件长度包含50 mm、80 mm、100 mm、150 mm，从分析结果可以看出，该组试件同样在30～40 mm左右时达到极限抗弯承载力，都将在加载后期发生局部屈曲破坏，组合梁抗弯承载力与连接件长度呈现正相关，见表4，但增加连接件长度对承载力提高效果并不显著。

3.3 π型连接件位置设置对组合梁抗性能影響

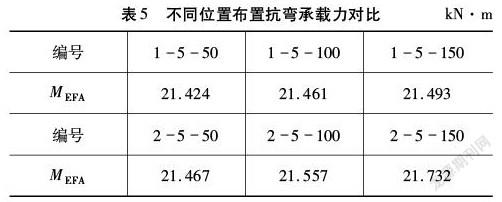
长度为50 mm，100 mm，150 mm的连接件在梁通长设置，与仅在加载中部纯弯段设置分析进行分析比较。从表5可以看出，同样数目的π型连接件，将其设置在中部纯弯段抗弯承载力提高效果优于连接件通长设置。值得注意的是，在纯弯段集中设置π型连接件，3种不同长度连接件的加载过程中均未出现明显屈曲现象，由图4可以看出，相比与全梁通长设置组，显著的控制了局部屈曲现象的出现。

4 结论

本文研究了含有π形连接件的双肢冷弯薄壁C型钢组合得到拼合梁的受弯性能。在ABAQUS有限元程序中，建立了具有几何缺陷的非线性有限元模型，分析了π形连接件在不同间距、不同长度及不同设置位置情况下，对组合梁的抗弯性能的影响。根据本文提出的结果，可以得出以下结论：

（1）所有实验组的组合梁都在跨中最大位移30～40 mm左右时达到极限抗弯承载力，随着π形连接件间距的减小、连接件长度的增加，组合梁的极限承载力将提高，但两者对承载力提高的效果并不显著。

（2）在同样个数连接件的条件下，将连接件通长设置对承载力的提高不如仅在纯弯段设置，此外，在纯弯段集中设置连接件能很好的控制组合梁局部屈曲现象的发生。

参考文献

[1] 周绪红，王世纪.薄壁构件稳定理论及其应用[M].北京：科学出版社，2009.

[2] 石宇，周绪红，苑小丽，等.冷弯薄壁卷边槽钢组合工字梁极限承载力计算的有效宽度法[J].土木工程学报， 2011， 44（ 6） ： 8-17.

[3] 石宇，周绪红，聂少锋，等.冷弯薄壁卷边槽钢组合工字梁极限承载力计算的折减强度法[J].工程力学，2011， 28（9）： 174-182.

[4] 赵阳，周天华，李东.螺钉间距对冷弯薄壁双肢拼合箱形截面短柱承载力性能的影响[J].钢结构，2018，33（12）：28-31.

[5] 聂少锋，孙玉金，陶莹，等.双肢开孔冷弯薄壁型钢拼合箱形截面立柱轴压性能有限元与理论分析[J].建筑结构，2018，48（11）：84-89.

[6] Wang L， Young B. Design of cold-formed steel channels with stiened webs subjected to bending. Thin-Walled Struct 2014;85：81-92.

[7] Zhang JH， Young B. Numerical investigation and design of cold-formed steel built-up open section columns with longitudinal stiffeners[J]. Thin-Walled Structures，2015，89.

[8] Wang H， Zhang Y. Experimental and numerical investigation on cold-formed steel C-section flexural members. J Constr Steel Res 2009;65：1225-35.

[9] 周绪红，李说，孔次融.冷弯型钢卷边槽型截面受压构件板组稳定性与极限承载力研究[D].长沙：湖南大学，1997.

[10] Karlsson Hibbitt， IncSorensen， ABAQUS. ABAQUS/Standard user’s manualvolumes I-III and ABAQUS CAE manual. Version 6.12. （Pawtucket， USA）; 2010.

[11] Schafer BW， Pekz T. Computational modeling of cold-formed steel： characterizing geometric imperfections and residual stresses. J Constr Steel Res 1998;47：193-210.

3849501908296