基于UDEC的桥基顺层边坡稳定性数值模拟分析

车铁成 龚洪苇 简波 邓涛 王陈宾 顾义

【摘 要】 桥基边坡稳定性直接关系到桥梁的施工与运营安全，山区桥梁基础位于顺层岩质边坡之上时形成桥基顺层边坡，其稳定性受到桥基荷载的影响，是工程界关注的热门问题。文章利用UDEC离散元软件对山区桥基顺层边坡的稳定性进行模拟分析。通过对桥基荷载施加前后顺层边坡的坡体位移与应力时程曲线变化规律对边坡稳定性进行评价，模拟计算结果表明：桥基荷载施加前后顺层边坡整体有沿着层理面发生滑动的趋势，滑裂面近似为直线形且最危滑裂面位于坡脚处。天然状态下的顺层边坡只受到重力作用，坡脚处应力集中，坡体内部应力随深度增大而增加;当施加桥梁荷载后桥基下方局部范围内岩体的应力显著增大，边坡各处位移均有增加，但仍满足规范对于边坡安全性的要求。

【关键词】顺层岩质边坡; 桥基荷载; 数值模拟; 位移; 应力; 稳定性

随着我国西部大开发以来，西部山区公路交通得到快速发展，在大规模的公路建设中，要穿越各种复杂地形地貌[1-2]，为保障线形要求，桥梁工程被大量使用，使得部分桥基不可避免地位于顺层边坡之上，由于桥基边坡稳定性對施工以及运营安全的影响，一直以来是受到工程界的关注。部分学者对桥基边坡稳定性进行了研究，罗彦彪[3]、赵亚飞[4]采用简化Bishop法和Morgenstern price法，而张爱军[5]、邹启贤[6]通过有限元强度折减数值法进行分析。刘佑荣[7]进一步将块体极限平衡理论与非线性弹塑性有限元相结合分析桥基斜坡稳定性。ZHAN Zhi-feng[8]利用工程地质方法分析桥基荷载作用下峡谷区边坡的稳定性。张雷[9]利用FLAC和ANSYS数值软件分析桥基荷载的岩质边坡稳定性。另有部分学者研究了顺层边坡的稳定性，高永涛[10]、闫佐菲[11]、杨博[12]对顺层岩质边坡变形破坏过程以及稳定性开展数值分析，而杨博[12]考虑了桥基荷载下的顺层边坡稳定性。

目前学者研究岸坡稳定性分析主要对桥基荷载或顺层边坡进行单因素分析，而对两因素综合比较分析桥基顺层边坡稳定性研究仍然较少。因此，本文结合实际工程，利用UDEC离散元数值模拟软件对桥基荷载施加于顺层岩质边坡之上的稳定性进行计算分析，对比分析坡体位移与应力的变化规律以及边坡稳定性系数，以此对桥基顺层边坡整体稳定性进行评价。

1 工程概况

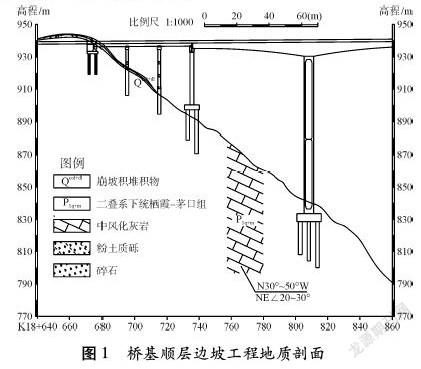
某连续钢构桥位于会东县大崇境内金沙江左岸一级支流雀依河中下游的庙梁子附近，属中高山地貌，地形起伏大，岸坡坡角25～ 55°，平均坡角40°。坡高826 m，两岸基岩均出露，地层岩性为二叠系下统栖霞-茅口组灰岩。边坡上部覆盖层厚2～5 m，主要为粉土质砾，坡体基岩裸露，为中风化灰岩，岩层倾向N30°～50°W，倾角NE∠20°～30°，层理间距4～9 m（图1）。根据现场地质测绘及钻探、物探揭示，桥址区无大规模地质构造发育。

2 计算模型及参数

2.1 计算模型

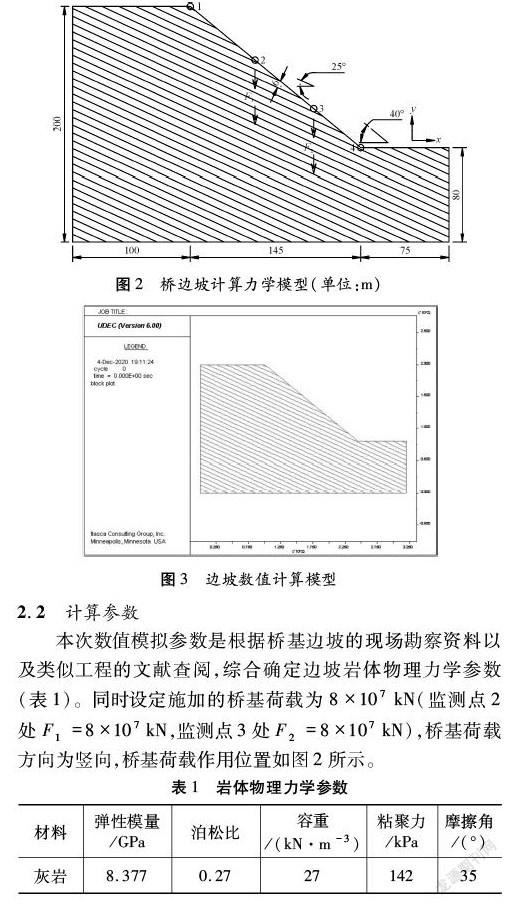
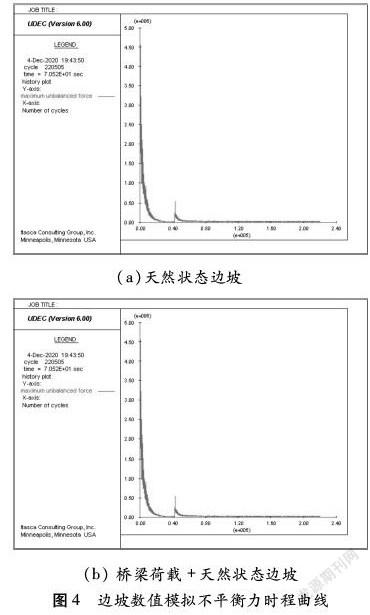
根据调查桥址区两岸边坡岩性及岩体结构特性等实际工程地质条件，假定边坡岩体应力-应变为理想弹塑性的本构关系，岩体破坏服从C-M准则[13]。本文主要模拟顺层岩质边坡施加桥基荷载作用对边坡稳定性的影响。依据现场地质资料，对桥基边坡进行简化，其中桥基作用依据张雷[9]对桥基荷载作用后边坡稳定性分析的数值模型简化，将桥基等效于作用力施加于边坡之上，进而开展数值运算。故建立二维边坡计算模型（图2），边坡模型尺寸为坡顶宽度100 m，坡高200 m，坡宽320 m，边坡底部至边界宽度为75 m，边坡底边界至底面为80 m，边坡坡向40°;同时为计算方便，选取层理倾角为25°，层理间距按6 m且等厚层计算。采用UDEC离散元数值分析软件，因计算范围大，网格划分较密，需对模型左右两侧加X方向约束，底部加Y方向约束（图3）。为进一步分析施加桥基荷载前后的边坡变化规律，将设四处监测点进行时程分析，其中监测点1、2分别为边坡坡顶、坡脚处，监测点2、3为桥基荷载施加的位置（图2）。

2.2 计算参数

本次数值模拟参数是根据桥基边坡的现场勘察资料以及类似工程的文献查阅，综合确定边坡岩体物理力学参数（表1）。同时设定施加的桥基荷载为8×107 kN（监测点2处F1=8×107 kN，监测点3处F2=8×107 kN），桥基荷载方向为竖向，桥基荷载作用位置如图2所示。

2.3 计算工况

本次边坡模拟主要考虑两种工况：

工况1：天然状态下（仅受重力作用）;

工况2：桥基荷载+重力作用。

3 模拟结果与分析

3.1 最大不平衡力的收敛性

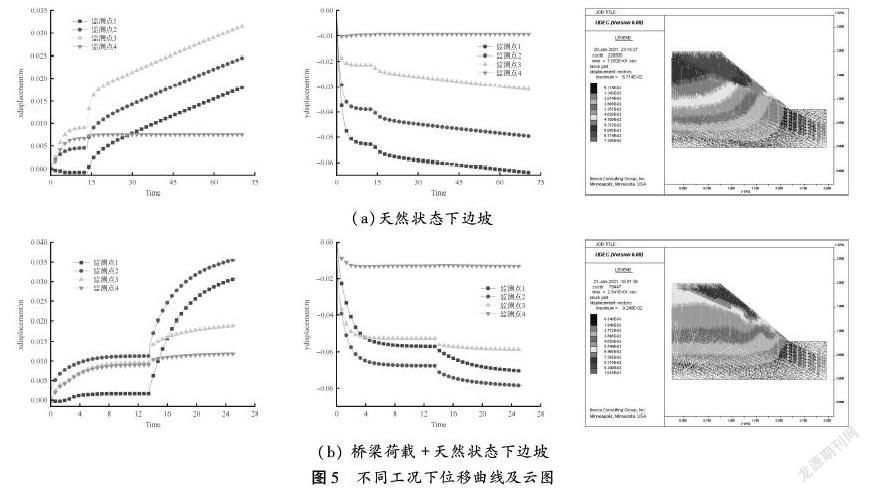
不管是天然状态下的边坡还是施加桥基荷载下的边坡，进行离散元运算过程中都有一个内力消散的过程，就是不平衡力的传递与分配过程[9]。当外荷载作用于边坡后，模型整体形成一个稳定的力场，此时边坡处于稳定状态。若边坡的最大不平衡力时程曲线不断波动当处于低谷时由于微小的扰动使得不平衡力随时间增加而增大，块体的速度及位移均产生明显的变化。从图4中可以看出随着时步的增加最大平衡力由最大值逐步降低，最终趋近于零由此判断边坡处于稳定状态中。

3.2 位移变化

针对两种边坡模型开展离散元数值模拟，为此设置四处监测点进行数据时程监测。由图5边坡位移变化时程曲线所示，各监测点的位移变化趋势基本一致，首先各监测点位移变化由增大而趋于初次平稳，后随着时步增大而呈近线性增长，反观坡脚位移变化增大而趋于稳定，未出现大幅度增大的趋势，原因在于边坡坡脚处发生变形后受到下部岩体的阻挡。对天然状态下的边坡只因受重力作用，由监测点2、3可知坡腰中部沿水平方向的位移变化最大，其位移分别达到4 mm、8 mm，坡脚处位移为7 mm，而坡顶初始阶段变化较小，主要沿竖直方向位移变化最大可达到52 mm;当施加桥基荷载于边坡之上，由监测点2、3可知施加作用力F1、F2位置的位移变化最大，其位移分别达到11 mm、9 mm，坡脚处位移为8 mm，沿竖直方向坡腰处位移最大可达到65 mm。区别于天然边坡当施加桥基荷载后，位移变化经过初次平稳阶段后随着时步增大位移有再次趋于平稳的趋势，究其原因在于施加桥基荷载后，坡体应力重新分布，使得位移发生不同的变化规律。从图5位移云图所示不管是天然状态下的边坡还是施加桥梁荷载下的边坡，边坡整体主要沿着层理面发生滑动，滑裂面近似为直线形且最危滑裂面位于坡脚处。

3.3 应力变化

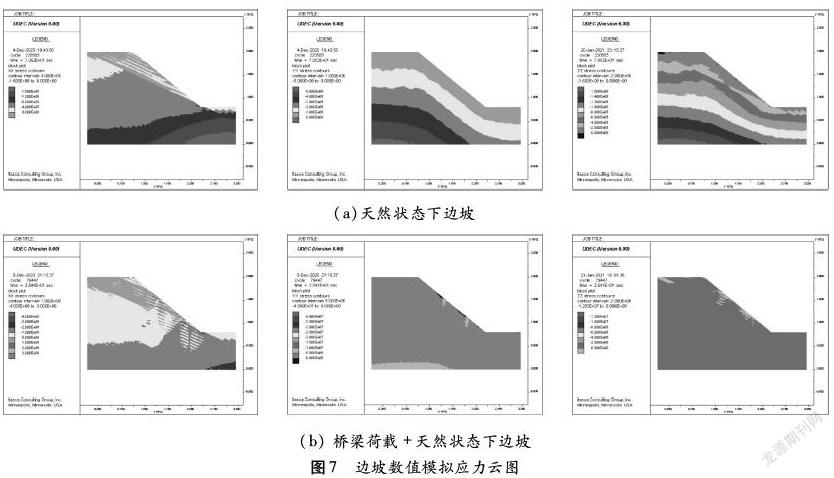
开展两种工况下边坡模型的离散元数值运算，对其应力分布进行分析，由图6边坡应力变化时程曲线可对各监测点的应力变化趋势开展分析，从初始阶段应力波动至应力的平衡。天然状况下的边坡受沿水平与竖直方向的应力变化趋势，各监测点受力在初始阶段的增大逐步趋于平衡后除坡脚位置均出现应力递减的趋势变化，而坡脚处的应力增加明显。当施加桥基荷载作用的边坡应力变化时程曲线，其各监测点应力变化范围均大于自然边坡的受力情况，位于坡腰和坡脚处的应力变化较为明显，而坡顶的应力变化基本趋于稳定。从图7所示天然状态下的边坡应力分布应力变化主要集中于坡顶附近，当施加桥梁荷载的边坡应力分布云图，最大主应力位于施加桥基荷载处。究其原因在于对于自然条件下坡体只考虑体力的影响，坡脚处出现应力集中现象，坡体内部应力随深度增加而增加;当施加荷载后主要影响桥基荷载作用点下方一定范围内岩体的应力状态，对岩体应力状态影响深度较大;坡体内部的应力分布受层面影响较显著。

3.4 稳定性分析

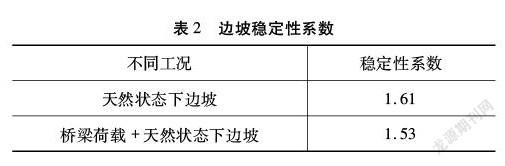
由表2可知利用数值运算得到的天然边坡下稳定性系数FOS=1.61，而施加桥基荷载下后边坡稳定性系数FOS=1.53，均满足JTG D30-2015《公路路基设计规范》中要求的最小界限，此时边坡处于稳定状态。

将各监测点的位移与应力曲线进行分析，对边坡整体而言应力随着位移的增大而趋于稳定，产生位移变化较小而坡体受到的应力变化较大，边坡均趋于稳定状态。天然状态下边坡的坡脚处沿水平方向的应力最大，随着应力增大位移出现递增趋势，坡顶和坡腰处的竖向位移变化较大，因坡脚处出现应力集中现象，坡顶处受力主要受到顺层边坡岩体层面的影响较大;当施加桥梁荷载后位移增大趋势显著，而坡顶处的位移-应力变化较小，主要发生变化的位于坡腰处，与天然边坡相比各监测点的位移-应力变化显著，坡脚的变化最终趋于平稳的趋势，究其原因荷载作用下对坡体内部一定范围的应力状态产生影响，使得坡体内部应力重分布后使得位移-应力变化较大。

4 结论

采用UDEC离散元软件对实际工程的桥基顺层边坡稳定性进行数值分析，建立两种工况下数值模型，对比分析坡体的位移与应力的变化规律以及边坡稳定性系数。

（1）桥基荷载施加前后顺层边坡整体有沿着层理面发生滑动的趋势，滑裂面近似为直线形且最危滑裂面位于坡脚处。

（2）在天然状态下边坡主要受到层理面的显著影响，当施加桥基荷载后边坡坡腰、坡顶与坡脚位移均有增加，边坡的最大的主应力位于桥基下部，桥基荷载的作用使得坡体内部的应力显著增大。

（3）通过数值运算得到了两种工况下的边坡稳定性系数，其中天然状态的边坡稳定性系数为1.61，施加桥基荷载于边坡之上后边坡的定性系数降低为1.53，该桥基边坡稳定性满足规范对于边坡安全性要求。

参考文献

[1] 廖军，龚洪苇，石磊，等.降雨作用下近水平红层公路高边坡渗流场特征研究[J].水力发电，2020，46（10）：47-51+62.

[2] 廖军，董谦，梁洪永，等.近水平红层公路隧道围岩分级指标初探[J].现代隧道技术，2020，57（3）：25-29.

[3] 罗彦彪，李春峰，罗勇.库区水位对高速公路桥梁边坡稳定性影响研究[J].公路交通科技（应用技术版），2017，13（11）：208-210.

[4] 趙亚飞，欧鸥.龙滩库区某公路大桥边坡稳定性分析[J].中外公路，2012，32（2）：36-39.

[5] 张爱军，莫海鸿.有限元强度折减法中边坡失稳位移突变判据的改进[J].岩土力学，2013，34（S2）：332-337.

[6] 邹启贤，申思冉，罗昌宏，等.基于FLAC3D的某桥头边坡稳定性数值模拟分析[J].安全与环境工程，2012，19（4）：133-136.

[7] 刘佑荣，贾洪彪，唐辉明，等.湖北巴东长江公路大桥斜坡稳定性研究[J].岩土力学，2004（11）：1828-1831.

[8] ZHAN Zhi-feng， XIE Qiang， ZHAO Wen. Analysis method research on rocky slope stability of bridge foundation in gorge area[J]. Journal of Sichuan University（Engineering Science Edition）， 2003， 35（6）： 31-35.

[9] 张雷，王孟渝，叶勇，等.考虑桥基荷载的岩质边坡稳定性数值模拟研究[J].地下空间与工程学报，2009，5（S1）：1331-1335.

[10] 高永涛，肖术，吴顺川，等.顺层岩质边坡变形破坏特征及稳定性数值模拟[J].工程科学学报，2015，37（11）：1403-1409.

[11] 闫佐菲，曾令强.重力作用下顺层岩质边坡破坏机理数值模拟研究[J].矿产与地质，2020，34（1）：183-188.

[12] 杨博，吴光，何刘，等.金沙江特大桥桥基岸坡稳定性的离散元法数值模拟分析[J].铁道建筑，2010（11）：13-16.

[13] 胡卸文，朱海勇，吕小平，等.大跨度高塔柱桥基边坡稳定性研究[J].岩石力学与工程学报，2007，26（z1）：3177-3182.

3857501908259