具有双时滞的分数阶BAM神经网络模型的动力学行为
2022-03-18李冰冰廖茂新李伟南
李冰冰,廖茂新,李伟南
(南华大学 数理学院,湖南 衡阳421001)
0 引 言
近几十年,双向联想记忆(bidirectional associative memory,BAM)神经网络具有自学习、自组织和自适应性及大规模并行处理等优点,其在优化求解、智能控制和模式识别等方面均有广泛的应用。关于神经网络的研究最早可追溯到20世纪40年代,但直到20世纪80年代神经网络才开始受到国际上学者的重视从而得到稳步发展。1984年J.J.Hopfield建立简化的神经网络模型[1]和1989年C.M.Marcus提出具延迟的神经网络模型[2],之后为了有效地掌握延迟神经网络模型的内在规律,许多学者开始研究神经网络的动力学行为[3-7]。文献[8-9]均研究了具有五个神经元的整数阶BAM神经网络模型,并以时滞之和作为参数给出了系统平衡点稳定性和产生Hopf分支的充分判据。
由于分数阶时滞微分系统相对整数阶可以更加准确地描述系统的动态行为,其被广泛应用在控制系统、复杂网络、金融系统等领域,目前学者们关于分数阶微分动力系统的研究也取得了大量成果(如文献[10-16]等)。常用的分数阶导数定义有Riemann-Liouville导数、Caputo导数和Grunwald-Letnikov导数。考虑到Caputo导数更易选取初值,本文采用Caputo型分数阶导数进行计算。为得到本文的主要结果,现给出如下定义与引理。
定义1 Caputo型分数阶导数[17]定义为
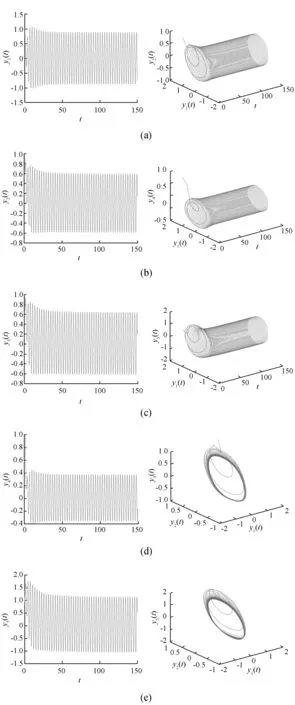
其中n-1 Caputo分数阶导数的拉普拉斯变换形式为 n-1 若f(l)(0)=0,l=1,2,…,n,则L{Dqf(t);s}=sqF(s)。 引理1[18]考虑具有多个状态变量的分数阶线性系统 (1) 其中q∈(0,1](i=1,2,…,n)。系统(2)的特征方程Δ(s)如下 若方程det(Δ(s))=0的所有根s的实部均为负值,则系统(1)的零解是Lyapunov全局渐近稳定的。 基于以上思想,本文建立如下具有双时滞的分数阶BAM神经网络模型。 (2) 在模型(2)中,Dq表示Caputo型导数且满足0 为得到本文主要结果,现给出假设: (H1)fi∈C1,fi(0)=0,i=1,2,…,5。 本文分为三个部分。在第1节中,通过分析分数阶系统(2)的线性化形式的特征方程,讨论了系统平衡点渐进稳定性和产生Hopf分支的条件。在第2节,通过一个实例进行仿真模拟,验证了理论结果的正确性。最后,在第3节给出主要结论。 现作如下变换 从而得到系统(2)的等价形式为 (3) 由(H1)可知,系统(3)的零点是其平衡点。且求得系统(3)的线性化形式如下 (4) 分数阶系统(4)的特征方程为 即 λ5q+c4λ4q+c3λ3q+c2λ2q+c1λq+c0+ (d3λ3q+d2λ2q+d1λq+d0)e-λτ=0, (5) 其中 c0=α1α2α3α4α5, 下面讨论分数阶系统(3)在平衡点处的稳定性。为后续工作顺利进行,给出如下假设: 当τ=0时,方程(5)变为 (6) 取s=λq,则方程(6)变为关于s的一元五次方程,即 (7) 因为 Δ1=c4=k0>0, k4>0, k1Δ4>0。 接下来研究当时滞τ>0时对分数阶系统(3)零平衡点的稳定性与周期解存在性的影响。 为后续工作顺利进行,现给出如下假设 (H3)方程(14)至少存在一个正实数根。 引理2 若假设(H3)成立,则特征方程(5)至少存在一对纯虚根。 证明:若方程(5)存在纯虚根,不妨将λ=iw代入式中,则有 (8) 将式(8)实部与虚部分离,则可得如下方程 E1coswτ-E2sinwτ=-E3, (9) E1sinwτ+E2coswτ=-E4, (10) 其中 由方程(9)和方程(10)计算得到 (11) (12) 且将方程(9)与方程(10)两边同时平方再相加求得 (13) 则可以得到关于w的方程如下 λ10q+e9λ9q+e8λ8q+e7λ7q+e6λ6q+e5λ5q+ e4λ4q+e3λ3q+e2λ2q+e1λq+e0=0。 (14) 式中 2d1d3cosqπ, 则由(H3)知,方程(14)存在有正实数根。不妨设方程(14)有N个实根并记为wk,k=1,2,…,N。将wk代入方程(11)中,则有 (k=1,2,…,N;j=0,1,2,…)。 (15) 此时±wk是方程(5)的一对纯虚根。即特征方程(5)至少存在一对纯虚根。证毕。 引理3 若假设(H4)成立,则系统(3)横截性条件满足。 证明:设λ(τ)=α(τ)+iw(τ)是方程(5)在τ=τ0附近使得α(τ0)=0,w(τ0)=w0的根,下面求横截性条件。对方程(5)关于τ求导,可得 (5qλ5q-1+4qc4λ4q-1+3qc3λ3q-1+2qc2λ2q-1+ (16) 即 其中 K(λ)=(5q-2τ)eλτλ5q-1+(4qc4-2τc4)eλτλ4q-1+ ((3qc3-2τc3)eλτ+(3qd3+d3τ))λ3q-1+ ((2qc2-2τc2)eλτ+(2qd2+d2τ))λ2q-1+ ((qc1-2τc1)eλτ+(qd1+d1τ))λq-1+ (d0τ-2τc0)eλτ, L(λ)=(d3λ3q+d2λ2q+d1λq+d0)λ。 现定义实数K1,K2,L1与L2如下 K(iw)=K1+iK2, L(iw)=L1+iL2, (17) 即K1,L1与K2,L2分别表示K(λ)与L(λ)在τ=τ0(此时λ=iw0)处的实部与虚部。 则由假设(H4)可得到 (18) 即横截性条件满足。证毕。 由1.1节及引理2与引理3可以得到如下定理。 定理1 若假设(H1)~(H4)成立,则当τ∈(0,τ0]时,分数阶系统(3)的零平衡点是局部渐近稳定的,且在τ=τ0时丧失稳定性并产生Hopf分支。 给出一个数值算例来支持理论分析。 考虑如下系统 (19) 图1 系统(19)的零平衡点渐进稳定(τ=0.65<τ0)Fig.1 The zero equilibrium point of the system (19) is asymptotically stable (τ=0.65<τ0) 图2 系统(19)的零平衡点失去稳定性并产生Hopf分支(τ=0.8>τ0)Fig.2 The zero equilibrium point of system (19) loses stability and produces Hopf bifurcation (τ=0.8>τ0) 图3给出了系统(19)产生Hopf分支的临界值随分数阶的阶数变化的情况,q=1时系统(19)为整数阶系统。 图3 当分数阶的阶次发生变化时,系统(19)产生Hopf分支的临界值的变化情况Fig.3 System (19) produces cases where the critical value of Hopf bifurcation varies with the order of the fractional order 时滞神经网络具有十分丰富的动力学行为,其在全局优化、信号处理和人工智能等问题都有重要应用。因此研究此类系统的动力学行为在解决理论和实际问题过程中都是十分有效且适用的。本文研究了一类具有双时滞的分数阶简化BAM神经网络的动力学行为,通过将两个时滞之和τ=τ1+τ2看作分支参数,研究了该系统的动力学特性,并建立了Hopf分支发生的一些充分条件。通过分析发现时滞会影响分数阶系统的稳定性,当τ超过临界值τ0时,非线性时滞系统的零解会失去稳定性,出现Hopf分支。并通过仿真算例说明了本文主要结果的有效性和可行性。并且通过仿真发现,分数阶的阶数也会对系统产生Hopf分支的临界值有一定的影响,当选取较大的分数阶阶次时,会使得分数阶系统产生Hopf分支的时间点提前。1 模型的动力学分析
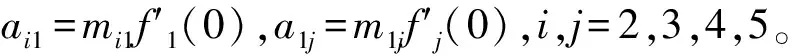
1.1 平衡点的稳定性
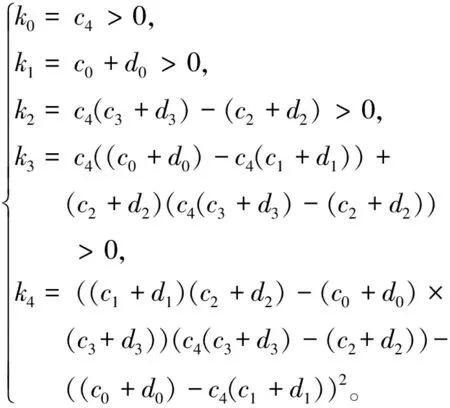
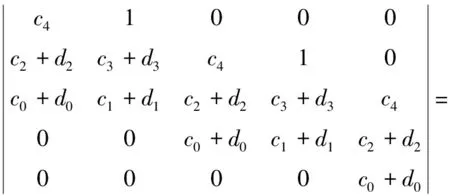
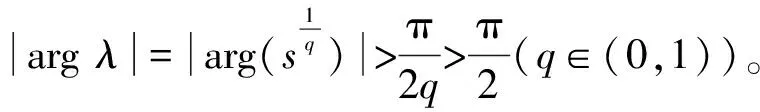
1.2 模型Hopf分支的存在性




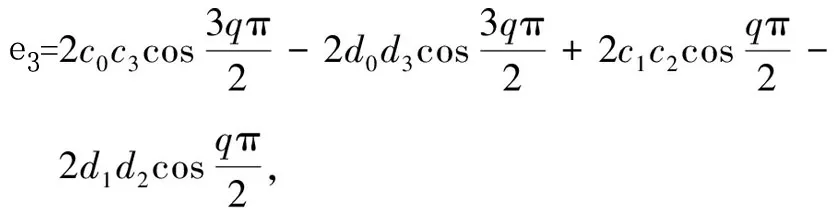

2 数值模拟



3 结 论
