中高应变率下泡沫金属动态拉伸有限元模型研究
2022-03-18张晓阳谭仕锋刘泽宇
张晓阳,谭仕锋,刘泽宇,赵 飘
(1.南华大学 数理学院,湖南 衡阳 421001;2.南华大学 土木工程学院,湖南 衡阳 421001)
0 引 言
泡沫金属是一种新型工程材料,具有质轻、吸能性强、比强度高、比表面积大等多种优异的物理与力学性能[1-8],在航空航天、建筑、电极装置等领域中具有广泛应用的应用前景[5-10]。泡沫金属材料在实际应用时往往承受动态复杂工况,发生拉伸破坏行为,因此,研究泡沫金属单轴动态拉伸力学性能是重要的科学问题,有助于完善其本构关系。
目前,国内外对泡沫金属的动态性能的研究主要集中在压缩冲击方面,包括分离式霍普金森压杆实验以及落锤实验技术[11-18]。然而,受实验技术条件限制,动态拉伸研究涉及很少,习会峰等[19]通过对试件两个端部涂胶并粘贴金属片进行夹持端补强,并采用由美特斯工业系统(mechanical testing and simulation,MTS)伺服液压式高速拉伸试验机对长方体泡沫金属试件进行拉伸加载,得到了50 s-1应变率拉伸下泡沫金属的一些简单的力学性能,受实验设备的限制未能做更高应变率的加载实验。为避免泡沫金属高应变率下会产生边缘局部破坏的现象,本文基于建立均匀规则的立方体3D Voronoi模型[19],通过改变加载路径的方式,并定量研究即设加厚倍数参数对动态拉伸模型的破坏形态与力学性能的影响,得到了一种适合高速拉伸的有限元模型(finite element models,FEM)及其加载方案。
1 细观模型的建立
随机3D Voronoi模型能够更好地描述泡沫金属材料内部细观结构的复杂无序。通过Voro++程序[20]生成边长为30 mm的立方体模型,模型设计为N个胞元随机分布,将模型导入前处理软件处理,网格尺寸为0.13 mm的S3R与S4R的混合网格(如图1(a)所示),导入到ABAQUS中,建立单轴动态拉伸有限元模型(如图1(b)所示)。基体材料为纯铝,密度为2 700 kg/m3,泊松比为0.33,屈服强度为80 MPa,弹性模量为70 GPa。胞孔平均等效孔径d0与真实泡沫金属试件的平均等效孔径相同:3.25 mm。由公式(1)[21]计算出胞孔数量N为1 500,模型的相对密度ρ为14%,对应的胞壁厚度t0的值为0.137 326 mm。
(1)
其中,V0为模型体积,mm3;S为模型表面积,mm2。
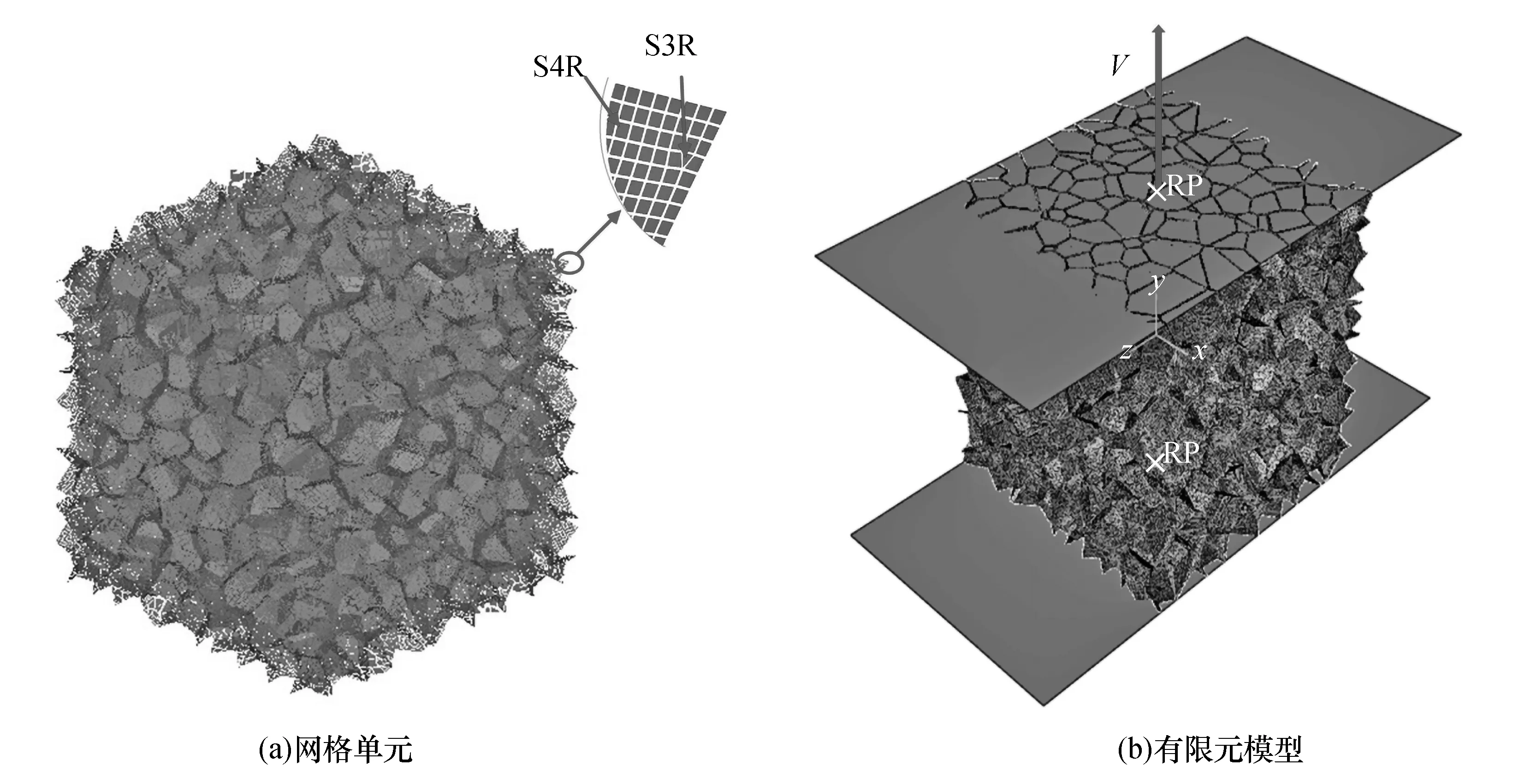
图1 泡沫金属网格划分及动态拉伸有限元模Fig.1 Meshed 3D Voronoi and dynamic tensile FEM
在模型上下表面分别设置一块解析刚体,来模拟实验中的压头。如图1所示,以试件模型的中心为坐标原点,将y轴正方向设置为加载端,负向设置为固定端。模型内部接触设置为通用自接触,而模型与解析刚体则设置为面面接触,切向摩擦系数设置为0.02。定义拉伸方向两端边缘1 mm区域的加厚倍数参数为k,如式(2)所示,
(2)
其中tmax表示模型单元胞壁厚度的最大值。设置两种加载方案如下:方案a是直接对模型以恒定的应变率进行拉伸加载;方案b先采用准静态应变率(0.5 s-1)进行预压0.001 5 mm和拉伸,使得名义应变为零,最后以预设的恒定应变率进行动态拉伸加载,加载路径设计对比如图2所示。

图2 两种加载路径对比Fig.2 Comparisons of two kinds of loading paths
为保证动态拉伸模型的合理性,应满足以下两个条件:1)保证其破坏位置的合理性;2)伪应变能与内能的比值不能超过10%[22],伪应变能与内能的比值越低,其计算结果精度越高。
2 实验设计及结果
2.1 改变加载路径对泡沫金属动态拉伸性能的影响
实验A组各模型的设计方案和建模参数如表1所示。当直接采用100 s-1对立方体模型进行动态拉伸时,A0模型出现明显的边缘局部破坏,如图3(a)所示,整个实验过程中的模型应力只存在边缘局部单元之中,并在边缘单元与解析刚体完全分离后迅速消失;而采用b方案加载的A1组、A2组模型破坏位置合理,但当应变率到达1 000 s-1时,采用方案b加载的模型,也出现了边缘破坏的现象。
从加载过程上来看,模型进入预压阶段时,由于预压时间极短模型内部单元并无应力产生,无单元屈服或者破坏,该预压阶段对后面的动态拉伸阶段的结果并无影响。预压过后的高速拉伸时刻由于惯性效应的作用,使模型内部应力瞬间增大,加载稳定后惯性效应逐渐消失。随着加载的进行,模型内部单元达到所能承载的极限应力后单元开始逐根断裂,并在短时间内形成一条贯穿模型的裂缝,此时模型被破坏。各模型对应的破坏图如图3所示,随着加载应变率的提高,各模型对应的破坏位置随之向加载端移动。直至应变率达到1 000 s-1时,模型出现零散的边缘胞壁单元与解析刚体分离的现象,该模型已无法合理地表征该应变率条件下泡沫金属的动态拉伸力学性能。

表1 A组动态拉伸模型加载方案及其加载参数Table 1 Loading scheme and parameters of dynamic tensile FEM

图3 A0-A3组模型动态拉伸破坏示意图Fig.3 Failure diagrams of A0-A3 models under dynamic tensile loading
从图4可以看出,实验A1和A2组在动态拉伸过程中,伪应变能与内能的比值未超过10%,数值模拟结果合理可靠。综上所述,通过改变加载路径的方式,能够实现最高900 s-1应变率条件下的泡沫金属动态拉伸力学性能测试。

图4 动态拉伸加载下模型伪应变能与内能之比Fig.4 Ratio of artificial strain energy to internal energy under dynamic tensile loading
应变率显著影响泡沫金属动态拉伸力学性能。A1组与A2组应力应变曲线对比如图5所示,在中低应变率(100 s-1)作用下,A1组模型的应力应变曲线具有明显的上升段以及峰值点,说明模型在破坏之前的加载就已经稳定状态,此时整个模型受到惯性效应的影响基本上可以忽略不计。然而,中高速应变率(900 s-1)拉伸时,模型的应力应变曲线呈现出递减趋势,在模型达到极限破坏应力时惯性作用并未完全消失。因此,受惯性效应影响,高应变率拉伸时泡沫金属无峰值应力特征,“峰值应力对应的状态就是破坏状态”的判据已经不再适用,需要探索新的适合高应变率拉伸的泡沫金属破坏判据。
2.2 改变加厚倍数对泡沫金属动态拉伸性能的影响
改变加载路径的方法,只能有限地提高动态拉伸应变率。为了实现更高的应变率,本文探究了提高加厚倍数参数k对泡沫金属动态拉伸力学性能的影响。
选取不同的边缘长度为1 mm区域内的单元胞壁厚度加厚k倍,其他参数以及加载路径b保持不变的情况下,生成B系列的模型,设计加载方案如表2所示。模型进行加载后的破坏图如图6所示,对比图6(c)、6(d)、6(e)可以发现随着加厚倍数的增加,模型破坏位置逐渐向中间移动,当加厚倍数k=7时,模型在1 800 s-1应变率拉伸时避免了端部局部破坏,因此,本文选取加厚倍数k为7。对比图5、图6可以发现,在100 s-1应变率的加载条件下,A1组与B1组模型的破坏位置、A2组模型与B2组模型的破坏位置基本相同,且破坏单元的初始坐标发现都不位于加厚段,说明胞壁厚度加厚倍数增大到一定数值后,增大参数k,不影响泡沫金属动态拉伸有限元模型的合理性。

图5 动态拉伸加载下应力-应变曲线对比Fig.5 Comparisons of the stress-strain curves under dynamic tensile loading
对比B1、B2、A1组和A2组模型的应力-应变曲线(如图7所示),从图7中可以看出,随着加厚倍数参数k的增大,边缘加厚区域单元质量也随之变大;相同应变率的加载条件下,与加厚0.3倍的模型相比,加厚7倍的模型在动态拉伸加载下呈现出更显著的惯性效应,且应力-应变曲线呈现显著的振荡特征,加厚倍数越大,将越不利于应力-应变数据的稳定性。因此,在保证模型破坏合理的前提下,尽量减小加厚倍数参数。
基于加厚倍数为7的B系列模型,探究其能实现的动态拉伸最大应变率。以100 s-1为基数逐步增大加载应变率,开展数值模拟实验。结果表明,加厚7倍的新模型相比于加厚0.3倍的模型,动态拉伸最大应变率显著提高。应变率1 800 s-1及以下动态拉伸时,模型的破坏位置合理(如图6(e)所示),直至应变率达到1 900 s-1时,破坏单元开始延伸至加厚区域。B5组与B6组的破坏示意图以及其应力-应变曲线分别如图6(e)、6(f)和图8所示。对比可以发现,B6组的初始应力显著的大于B5组的结果,该结果验证了B6组模型的破坏位置不合理。因此,边缘胞壁厚度加厚7倍的方法,能实现的动态拉伸最大应变率为1 800 s-1。综上所述,通过改变边缘胞壁加厚倍数的方法,可以极大地提升泡沫金属动态拉伸的最大应变率,促进泡沫金属单轴和多轴动态拉伸力学性能测试技术的发展和相关力学性能的研究。
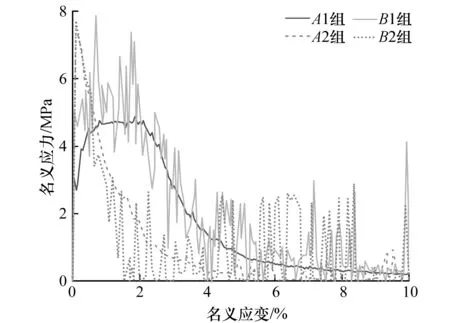
图7 A1、A2、B1和B2组模型动态拉伸加载下应力-应变曲线Fig.7 Stress-strain curves of A1, A2, B1 and B2 models under dynamic tensile loading

表2 B组动态拉伸模型加载方案及其参数统计Table 2 Modeling loading scheme and parameter statistics

图8 B5、B6组模型动态拉伸加载下应力-应变曲线Fig.8 Stress-strain curves of B5、B6 models under dynamic tensile loading
3 结 论
1)合理的改变加载路径和加厚边缘胞壁厚度的方法,均能够有效地避免泡沫金属边缘局部破坏的现象的发生,有效地提高泡沫金属动态拉伸测试的最大应变率。
2)边缘区域加厚长度为1 mm,加厚倍数为7倍的立方体模型采用静态预压后再反向拉伸形式,能够实现最高应变率达到1 800 s-1的泡沫金属动态拉伸测试方法。
3)泡沫金属模型在动态拉伸下的破坏位置与破坏模式与拉伸速率有关。破坏位置随着加载速率的提升而朝着加载端移动,破坏模式主要表现为拉伸断裂与剪切破坏两种;在中高应变率拉伸条件下,泡沫金属的应力-应变曲线无明显的峰值应力。
