分布随从力作用下黏弹性悬臂输流管道的稳定性分析
2022-03-18漆发辉王天林郭长青
漆发辉,王天林,郭长青
(南华大学 土木工程学院,湖南 衡阳 421001)
0 引 言
在流固耦合研究领域中,输流管道的振动与稳定性是一个经典问题,在水利、海洋、核能、航空航天和石油运输等实际领域都有着广泛的应用。由于其展现出来的丰富的动力学特性,越来越多的学者注意到了这个问题,并对其进行了研究[1-4]。
输流管道的黏弹性作为影响输流管道稳定性的内在因素之一吸引了许多学者的目光,使得他们对其展开了研究。王忠民等[5]对非守恒黏弹性输流管道系统的动力特性和稳定性进行了分析,并得到了松弛时间对黏弹性输流管道的稳定性有显著影响的结论。张战午[6]对黏弹性输流管道的动力稳定性进行了研究。赵凤群等[7]对简支黏弹性输流管道受分布随从力作用下的动力特性进行了分析。B.A.Khudayarov等[8]通过建立数学模型来研究黏弹性输流管道的非线性振动问题,并利用Bubnov-Galerkin方法,将该数学模型简化为一个以时间作自变量的常积分微分方程组的研究。最后的结果表明,管道的黏弹性会使其振动的频率和振幅均降低。Q.X.Huang等[9]研究了黏弹性输流管道在正弦流作用下的动力学特性,旨在改善此类流体相互作用系统的性能。刘颖[10]分析了黏弹性悬臂输流管道的稳定性。A.R.Askarian等[11]对具有Zener分数阶本构关系的黏弹性输流管道在不同边界条件下的稳定性进行了分析。
在实际的工程应用中,由于各种原因,输流管道的约束条件也会大不相同。输流管道在不同的约束条件下就会表现出各异的动力学特性。金基铎等[12]用实验研究的方法分析了两端固定的输流管道在脉动流作用下的参数共振问题。包日东等[13]研究了端部约束悬臂输流管道的分岔与混沌响应。J.D.Jin等[14]通过使用Galerkin方法离散运动微分方程,研究了支撑管道输送流体的稳定性。颜雄等[15]对两端弹性支承条件下的输流管道进行了研究,着重分析了非对称弹性支承下系统的固有特性。分析的结果表明,对称支承的刚度越大,系统的一阶固有频率下降越快;对于非对称弹簧支承的系统而言,流体流速越大,其对系统固有频率的影响越显著。
输流管道的稳定性除了受内在因素的影响之外,还与输流管道受到的外在因素的影响有关。分布随从力便是影响输流管道稳定性的外部因素之一,其可能来源于管道外流的黏滞力。
郭长青等[16]分析了分布随从力作用下的简支输流管道的稳定性。许锋等[17]研究了含裂纹输流管道在分布随从力作用下的振动与稳定性。J.H.Huang等[18]通过推导双参数地基上受分布随从力作用的输流管道的运动微分方程,研究了基础衬板刚度对固有频率和速度的影响。
本文在文献[10,16]的研究基础上综合考虑了输流管道的黏弹性和分布随从力两个因素,研究了黏弹性悬臂输流管道在分布随从力作用下的稳定性。分析了管道黏弹性系数、分布随从力大小以及输流管道和流体的质量比变化对输流管道振动特性和稳定性的影响。
1 运动方程
1.1 模型及运动微分方程建立
受分布随从力作用的黏弹性悬臂输流管道模型如图1所示,输流管道内流体的流速恒定,分布随从力与输流管道挠曲线始终保持相切。
管道采用Kelvin黏弹性模型和Euler梁模型,位置x处任意时刻t的挠度记为w(x,t)。运动微分方程为:
(1)
式中:E*为黏弹性系数,Pa·s;E为管道弹性模量,N/m2;I为管道截面惯性矩,m4;w为管道横向位移,m;L为管道长度,m;q为沿管道切线方向的分布随从力,N/m;M和m分别为流体和管道的单位长度质量,kg/m;U为管道内流体的运动速度,m/s。

图1 受分布随从力作用的黏弹性悬臂管道Fig.1 Viscoelastic cantilever pipe subject to distributed follower force
1.2 运动微分方程无量纲化
在式(1)中引入以下无量纲参数:
(2)
将式(1)无量纲化为:
(3)
2 数值求解方法
运用Galerkin方法求解无量纲化运动微分方程式(3)。令:
(4)
其中φi(ξ)为梁的第i阶振型函数。
悬臂管道的振型函数为:
(5)
其中λi满足特征方程:
coshλicosλi=-1
(6)
系数ci由式(7)给出:
(7)
将式(4)代入式(3),同时在方程左右两边乘以φj(ξ),然后在[0,1]区间对ξ积分,并利用振型函数的正交性可得:
(j=1,2,…,N)
(8)
为了求解方便,令
(9)
将二阶线性微分方程组式(9)化为一阶线性微分方程组:

(10)
其中系数矩阵B中的非零元素为:
(11)
3 计算结果与分析
通过采用不同的黏弹性系数α、分布随从力γ、流速μ和质量比β,从而可以求出B的特征值D。
特征值D可以用无量纲复频率Ω来代替表示:
Ω=-iD=ω-αi=ΩR+iΩI
(12)
当q=0时,问题退化为文献[10]的情况,这里取截取项数N=10时计算的结果与文献[10]基本吻合,故本文的截取项数取N=10。
3.1 临界流速随质量比、黏弹性系数和分布随从力的变化
图2给出了黏弹性系数α=0.01时,不同分布随从力γ作用下临界流速μc与质量比β的关系。从图2可以看出:在分布随从力作用下黏弹性悬臂输流管道的无量纲临界流速μc大致随分布随从力γ的增大而减小。在γ=50这条曲线上,流速为0时已经发生失稳,但当β>0.59时,系统可以在达到一定流速后再次获得稳定,如果流速继续增加,则系统又会变为失稳状态(稳定区域的划分:在临界流速曲线以内的为稳定区域,在临界流速曲线以外的为不稳定区域)。
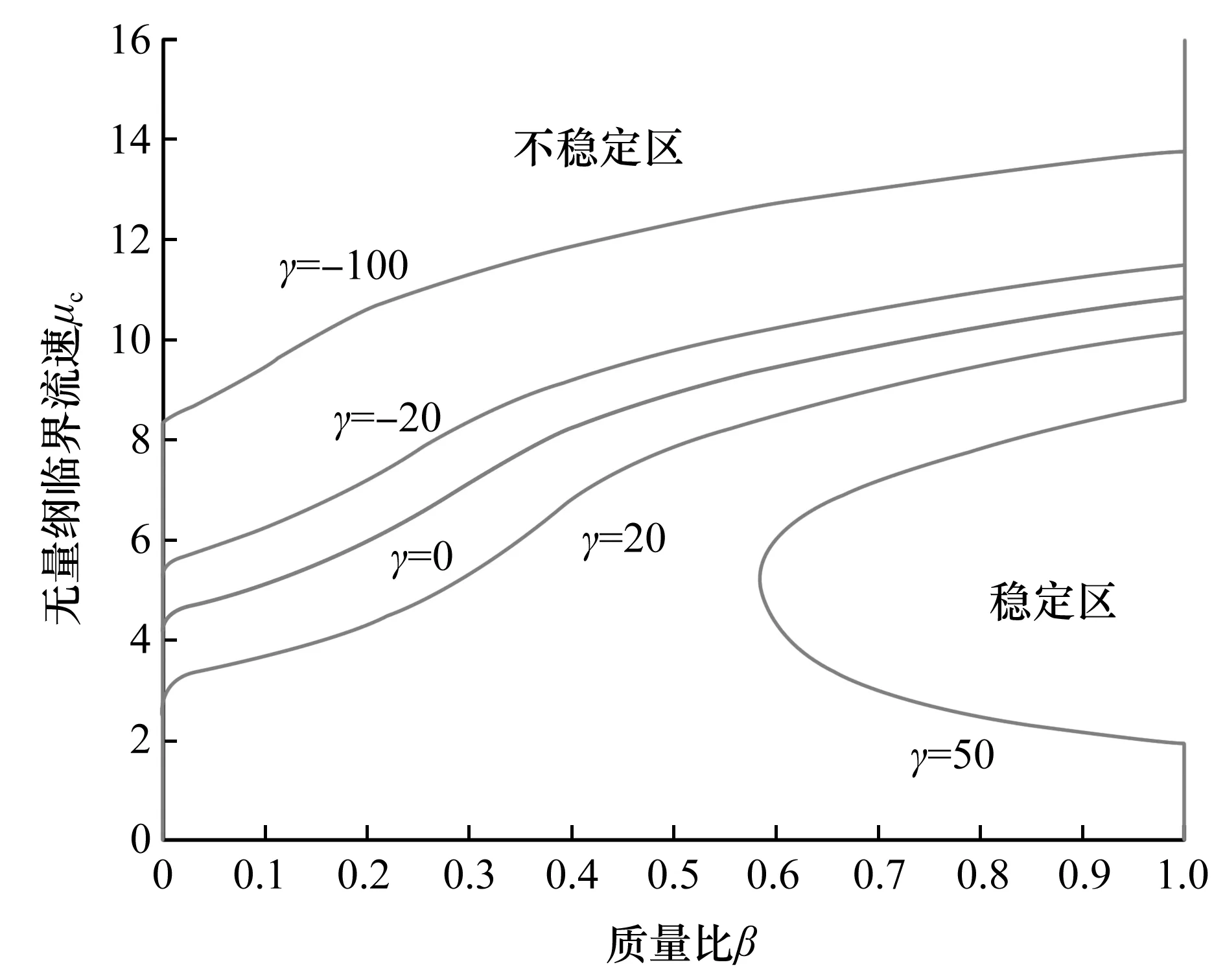
图2 黏弹性悬臂输流管道临界流速随质量比的变化(α=0.01)Fig.2 Variation of critical velocity with mass ratio in viscoelastic cantilever pipeline(α=0.01)
图3给出了黏弹性系数α=0.01时,不同质量比β作用下临界流速μc与分布随从力γ的变化关系。从图3可以看出:所有的曲线都汇聚相交在横轴上γ=22.41这个点,也即是分布随从力γ独自作用时的失稳临界值;在分布随从力γ<22.41时,系统存在一个低流速稳定区,而当分布随从力γ>22.41时,流速为零时就已经发生失稳,但是系统在增大到一定流速后会再次稳定。从图2和图3中均可以发现:随着质量比β的增大,系统的稳定区域也会进一步扩大。
图4给出了质量比β=0.2时,不同黏弹性系数α作用下临界流速μc与分布随从力γ的变化关系。从图4可以看出:当黏弹性系数α=0,临界流速μc随分布随从力γ单调递减;而当黏弹性系数α>0,分布随从力γ大于一定值时,随着流速的增加,系统则会经历失稳、稳定和再失稳三个阶段。说明黏弹性的从无到有使得系统有一个质变的过程。从整个图形来看,分布随从力γ<-41.71时,系统的稳定区域会随黏弹性系数α的增大而减小,此时黏弹性系数α不利于系统稳定。当分布随从力γ>-41.71时,系统的稳定区域会随黏弹性系数α的增大而增大,此时黏弹性系数α有利于系统稳定。

图3 黏弹性悬臂输流管道临界流速随分布随从力的变化(α=0.01)Fig.3 Variation of critical velocity with distributed dependent force in viscoelastic cantilever pipeline(α=0.01)

图4 黏弹性悬臂输流管道临界流速随分布随从力的变化(β=0.2)Fig.4 Variation of critical velocity with distribution and follower force in viscoelastic cantilever pipeline(β=0.2)
3.2 复频率随流速的变化
图5给出了质量比β=0.2,黏弹性系数α=0时,悬臂输流管道在不同分布随从力γ作用下的一、二阶复频率随流速μ的变化情况。从图5可以看出:当分布随从力γ=10时,系统一阶模态的实部在流速μ=5.93的位置等于零,但是此时它虚部的两个分支都为正值,因此一阶模态并不会发生发散失稳。在流速μ=4.68时,二阶模态的虚部由正变为负,且其实部始终为正值,所以二阶模态发生颤振失稳。分布随从力γ取0和5时的情况与分布随从力γ取10时的情况基本一致。综合来看,随着分布随从力γ的增加,系统二阶模态颤振失稳的临界流速会随之减小。
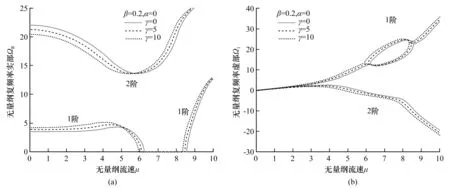
图5 不同分布随从力下悬臂输流管道前两阶复频率与流速的关系Fig.5 Relationship between the first two order complex frequencies and the flow velocity of a cantilever pipeline under different distributed follower force
图6给出了质量比β=0.2,黏弹性系数α=0.01时,黏弹性悬臂输流管道在不同分布随从力γ作用下的一、二阶复频率随流速的变化情况。从形状上来看,图6和图5大致是类似的。图6的一阶模态同样存在着一个复频率实部为0的区间,相应的虚部上也有两个分支,且这两个分支都为正,所以系统的一阶模态仍然是稳定的。系统二阶模态的虚部随着流速的增加由正值变为负值,而其实部一直为正值,所以系统二阶模态也同样会发生颤振失稳。由图6和图5比较可知,随着分布随从力γ的增加,系统的失稳临界流速会跟着减小,但是系统整体的稳定特性不会随之改变。

图6 不同分布随从力下黏弹性悬臂输流管道前两阶复频率与流速的关系Fig.6 Relationship between the first two order complex frequencies and the flow velocity of a viscoelastic cantilever pipeline under different distributed follower force
图7给出了黏弹性悬臂输流管道在不同质量比β作用下的一、二阶复频率随流速μ的变化情况。图7相较于图5和图6,出现了两个一阶复频率实部为0的区间。当质量比β=0.6时,这两个区间分别是流速为3.24≤μ≤4.90和8.74≤μ≤10.49。与之对应的一阶模态的虚部都为正值,所以系统的一阶模态没有发生发散失稳,处于稳定状态。系统的二阶模态虚部在流速μ=8.98时由正值变为负值,且其实部为正值,所以二阶模态此时发生颤振失稳。总的来说,二阶模态颤振失稳的临界流速随质量比β的增大而增大。

图7 不同质量比下黏弹性悬臂输流管道前两阶复频率与流速的关系Fig.7 Relationship between the first two order complex frequencies and the flow velocity of a viscoelastic cantilever pipeline with different mass ratios
图8给出了黏弹性悬臂输流管道在不同黏弹性系数α作用下的一、二阶复频率随流速μ的变化情况。从图8可以看出:当黏弹性系数α=0.03时,系统一阶模态实部在流速为4.88≤μ≤6.17的区间内为零,此时一阶模态的虚部为正值,因此系统一阶模态处于稳定状态。系统的二阶模态虚部在流速μ=6.05时由正值变为负值,但其实部为正值,所以二阶模态此时会发生颤振失稳。由图8可以得出,黏弹性系数α取值增大时,系统二阶模态颤振失稳的临界流速也会增大。

图8 不同黏弹性系数下黏弹性悬臂输流管道前两阶复频率与流速的关系Fig.8 Relationship between the first two order complex frequencies and the flow velocity of a viscoelastic cantilever pipeline with different viscoelastic coefficients
4 结 论
1)对于黏弹性悬臂输流管道,随着分布随从力的增加,系统的失稳临界流速会减小。
2)在分布随从力作用下,黏弹性悬臂输流管道失稳的临界流速会随质量比的增大而增大。
3)分布随从力γ>-41.71时,黏弹性系数增加,黏弹性悬臂输流管道的临界流速会略微增大,影响不明显。
4)分布随从力和黏弹性系数不会改变悬臂输流管道的稳定性,系统的一阶模态是稳定的,而二阶模态会发生颤振失稳。悬臂输流管道的失稳方式主要是颤振失稳,没有发现发散失稳的情况。
