具斥力函数的奇异Cucker-Smale模型的渐近免碰撞集群
2022-03-18徐兴海刘宏亮欧阳自根肖其珍
徐兴海,刘宏亮,欧阳自根,肖其珍
(南华大学 数理学院,湖南 衡阳 421001)
0 引 言
在自然界中,大量的生物体在成群结队运动时往往会形成稳定且规律的运动状态,如成群结队南飞的雁群、结伴捕猎的狼群以及草原迁移的野牛。这些群体现象表现出来的自发、稳定、协助一致的特征引起了生物、数学、控制等方面学者的广泛关注。如1986年,C.W.Reynolds[1]给出集群的三个核心要点:体积排斥、速度对齐和聚集倾向。1995年,T.Vicsek[2]从统计学的角度建立了后被称为Vicsek来刻画粒子集群行为。2007年,F.Cucker与S.Smale利用通信函数描绘个体间的相互作用,建立Cucker-Samle[3](以下简称C-S)模型,从数学方面阐述集群问题,其模型如下:
(1)
其中xi∈Rd,vi∈Rd,(i=1,2,3,…,N)分别表示第i个智能体在t时刻的位置和速度,φ(r)=1/(1+r2)β为通信权函数,K1是耦合强度。此后,该模型引起了许多学者广泛的关注,如R.Mauro[4]考虑了智能体间信息交互的延时性,并得到系统能够形成集群的充分条件。Y.Z.Sun[5]等人考虑了随机噪声干扰的情况,得出当通信函数存在正下界且噪声在某个可控范围时,集群仍然会发生的结论。J.H.Shen[6]提出具有等级制度下的集群模型后,并证明了在连续的情况下只要β≤1/2,系统就会发生无条件渐进集群。后来C.H.Li[7]离散系统的角度,照样获取了同样的结论。H.L.Liu[8-10]探究了有限时间集群,通过引用符号函数破坏系统的Lipschitz连续性来保证系统的有限时间集群性。S.Y.Ha[11-12]引入粒子间排斥力,证明了当系统的初始值限定在一定范围内,系统中的粒子就不会发生碰撞。F.Cucker与J.G.Dong[13-15]等引入合力函数和利用能量函数方法证明了当β<1时,系统达到无条件且免碰撞的渐进集群。β>1时,系统的初始值要满足一定的条件时才能到达免碰撞集群。特别地,J.A.Carrillo[16-17]使用奇异的通信函数φ(r)=1/rα来避免碰撞,得到当α≤2时会形成无条件免碰撞集群。
本文受参考文献[8,16]的启发,建立以下模型:
(2)
其中
且初值记为
(xi(0),vi(0))=(xi0,vi0),
(3)
‖·‖是欧式范数,R是智能体控制预设距离,K1,K2是耦合强度皆为正常数。
为了叙述上的方便,首先给出必要的假设以及集群的定义。

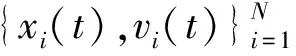
(4)
则称系统(2)~系统(3)形成免碰撞的渐进集群。
1 解的全局存在唯一性
为了说明系统(2)~系统(3)全局解的存在性,先给出位移差与速度的一致有界性引理。
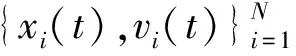
和
证明:设能量函数
(5)
沿着系统(2)对E(x,v)求关于t的全导数得

〈vi(t)-vj(t),(xi-xj)=
(6)
记
又因为E(x,v)在t∈[0,T)上非增非负,有E(x,v)≤E(0)。显然

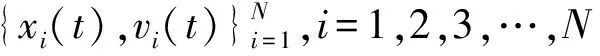
证明:设T>0。需要证明系统(2)在[0,T]上存在唯一解。然而,由于在t=0时粒子有不同的位置,且权函数仅在r=0处奇异,因此局部唯一光滑解是存在的。那么就有两种可能性:在区间[0,T]粒子不发生碰撞,解可以延拓到[0,T]。或者存在t0∈(0,T]第一次发生碰撞,那么解唯一存在且光滑的区间为[0,t0),假设这样的t0存在,然后根据它的定义,存在一个粒子S=1,2,3,…,N使得第S个粒子与其他一些粒子发生碰撞,用集合S表示这些碰撞粒子的集合,即有
其中,集合S中的元素个数|S|>1。同时设


2‖X(t)‖S‖V(t)‖S。
从而
(7)
另外
(8)
首先,对J1做估计。由于对称性,交换累加顺序易得
(9)
同理
(10)
根据式(9)和式(10),计算得
(11)
此外,注意到对任意i,j∈S,有
‖xi(t)-xj(t)‖≤‖X(t)‖S,
且φ(·)非增,于是
(12)

紧接着对J2进行分析。由φ(·)满足假设和L(δ)是Lipschitz常数,有
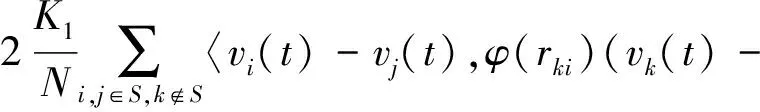
vi(t))-φ(rkj)(vk(t)-vj(t))〉+
vj(t),(φ(rki)-φ(rkj)(vk(t)-vj(t)))〉-
φ(rkj)(vk(t)-vj(t)))〉。
(13)
注意到在引理1中‖vk(t)-vj(t)‖≤2C,所以由Cachy-Schwarz不等式可得

4CJ2‖X(t)‖S‖V(t)‖S,
(14)

类似J1的方法,下面对J3进行估计

‖f(rki)(xk(t)-xi(t))‖≤
xi(t)‖m-R|×‖xk(t)-xi(t)‖m-1‖vk(t)-
vi(t)‖≤2CJ3‖V(t)‖S,
(15)

为了更好的对J4进行估计,先对f(rij(t))进行讨论,当i,j∈S,k∉S时,有‖xi(t)-xk(t)‖∈[δ,xc],此时f(rij(t))是闭区间上的连续函数,那么一定存在常数C1,C2有
‖f(rki)-f(rkj)‖≤C1‖rki-rkj‖,
‖f(rij(t))‖≤C2。
于是可得

vj(t),f(rkj)(xj(t)-xi(t))〉≤
‖(f(rki)-f(rkj))(xk(t)-xj(t))‖≤
‖xi(t)-xj(t)‖≤2CJ4‖X(t)‖S‖V(t)‖S,
(16)

联立式(12)~式(16),则有
4CJ2‖X(t)‖S‖V(t)‖S+2CJ3‖V(t)‖S+
2CJ4‖X(t)‖S‖V(t)‖S。
(17)
因‖V(0)‖S≠0,故‖V(t)‖S≢0,将式(17)左右两边同时约去2‖V(t)‖S,可得
2CJ2‖X(t)‖S+CJ3+CJ4‖X(t)‖S。
(18)
根据式(7),式(18)可化为
2CJ2‖X(t)‖S+CJ3+CJ4‖X(t)‖S。
(19)
将式(19)左右两边从0到t(t∈[0,t0))积分,


即


(20)
显然,式(20)的右边有界,而左边
这显然矛盾。因此解在[0,T]上存在且唯一。又由T是任意性,解最终可以延拓到无穷。也即t0→+∞,都有‖xi(t)-xj(t)‖≠0,i,j∈1,2,3,…,N,i≠j。证毕。
2 集群的充分条件
定理2 设定理2成立,那么系统(2)~系统(3)会形成免碰撞渐近集群。
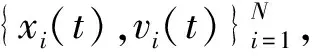

(21)
注意到在假设中,φ非增非负。又由式(21)可推出
E(0)-E(t)≤E(0)
(22)
从而,进一步得到
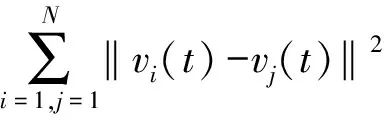

对‖V(t)‖2求关于t的导数得到

vj(t)),f(rki)(xk(t)-xj(t)))〉‖≤
2Nφ(xc)‖V(t)‖2+
2C2N‖V(t)‖‖X(t)‖。
(23)
3 仿真实验结果与分析

例1 设m=1.2,初始位移v0位于区间[-5,5]且不相同的随机数,初始速度v0位于区间[-5,5]的随机数。通过使用Python数值模拟,得到图1~图4。由图1,图2可得,粒子相对位移不变,粒子的速度趋于一致,即粒子形成了渐进集群。在图3,图4中可以看出粒子最大位移差一致有界,期间最小位移差恒大于0。那么无碰撞渐进集群是可达的,从而展现了第三节结果是合理的。

图1 粒子的位移Fig.1 Displacement of particles

图2 粒子的速度Fig.2 Speed of the particles

图3 粒子的最小位移差Fig.3 Minimum displacement difference of particles
例2 设m=1.8,初始位移v0位于区间[-5,5]且不相同的随机数,初始速度v0位于区间[-5,5]的随机数。如图5~图8所示,粒子经过一段时间后速度趋于一致,相对位移不变,粒子间最大位移差一致有界,全局过程中粒子间最小位移差恒大于0。那么无碰撞的渐进集群是可实现的。
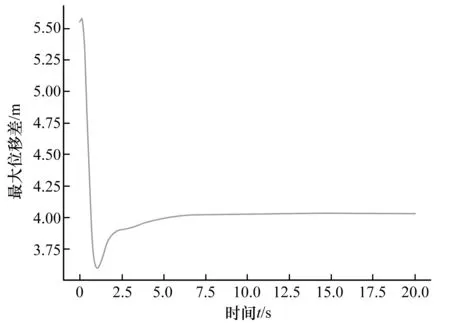
图4 粒子的最大位移差Fig.4 Maximum displacement difference of particles

图5 粒子的位移Fig.5 Displacement of particles
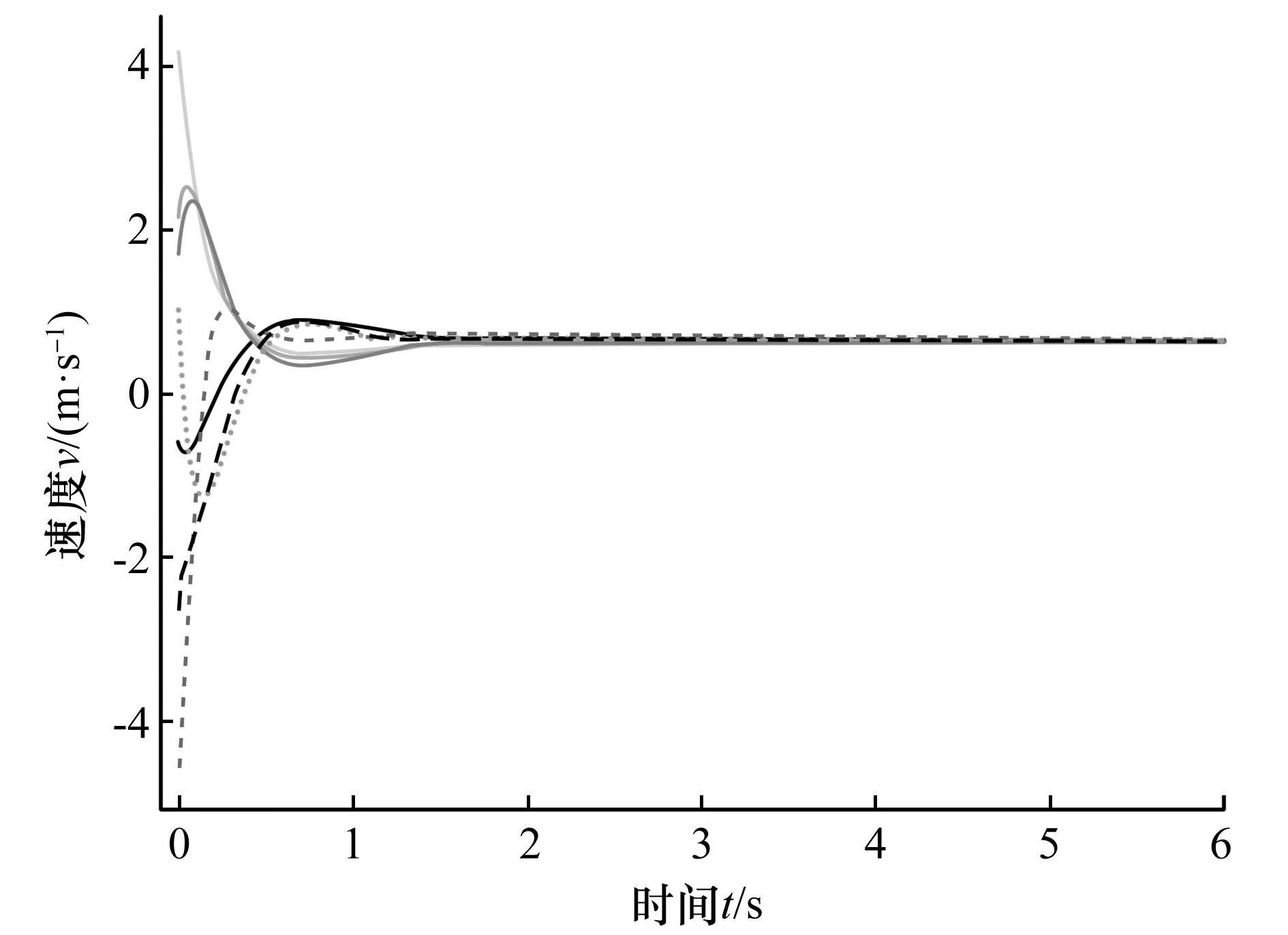
图6 粒子的速度Fig.6 Speed of the particles

图7 粒子的最小位移差Fig.7 Minimum displacement difference of particles

图8 粒子的最大位移差Fig.8 Maximum displacement difference of particles
4 结 论
本文对多智能体系统免碰撞集群做出了研究,通过排斥力与奇异值函数结合的方法来避免智能体集群的碰撞,将可能发生的碰撞问题转化为微分方程解的存在性问题,利用能量函数证明位移差的一致有界性与速度的一致有界性,在初值不发生碰撞的情况下,多智能体系统会形成渐进免碰撞集群。解决了多智能体系统的防碰撞问题,在无人机飞行应用中有重要实际意义。
