激光辐照光学窗口的温度场分析

易 瑔,戴颜斌,杨建昌,张宇航

(陆军装甲兵学院兵器与控制系,北京 100072)

1 引 言

在军事上,如何干扰和反制敌方的观察设备或制导导弹,一直是地面部队关注的难题。随着激光技术的进步,小型化、高功率的激光武器系统逐渐成为可能,世界各国都在加紧研制用于反导、干扰的激光武器[1]。辐照激光在对抗光电侦查系统时,往往首先作用到系统的窗口材料上,随着能量的注入使目标温度上升,最后达到高温熔融或者应力破裂的效果。因此,研究激光辐照窗口材料的温度场,有利于厘清激光破坏窗口材料的机理,进一步为激光武器的指标设计、性能优化提供科学理论。

对于玻璃材料的温度场分析,国内外有许多研究成果[2-7]。但有些研究将模型等效为无限大或半无限大平板,采用一维的热传导模型研究,忽略热量在平面方向上的扩散；有些采用二维热传导模型研究靶材表面的温度分布,虽然温度分布规律在热平衡之前是相同的,但是因为将边界条件设置为绝热,与实际情况差异较大。因此,为弥补上述不足,并为军用激光武器的设计选型提供理论依据,本文基于傅里叶定律的三维的热传导模型,设置换热的边界条件,计算得到其解析解,并对不同窗口材料的辐照情况进行计算和仿真,分析温度场变化的规律。

2 三维温度场理论模型

本文研究的对象是形状为平行平板玻璃的光学窗口,在温度场分析中假设长宽都为A,厚度为B,如图1所示。

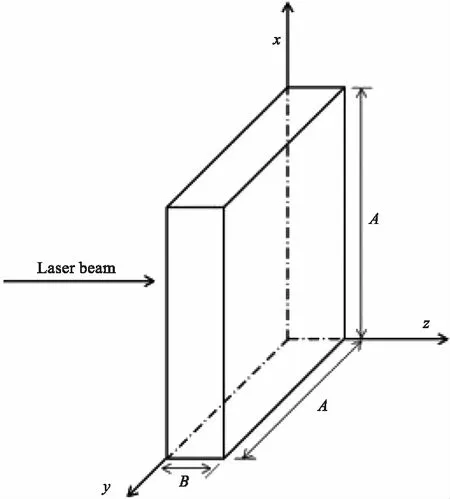
图1 物理模型示意图

考虑到窗口玻璃的厚度一般远小于长、宽,玻璃正面和背面的热交换远大于四条窄边,因此在模型中假设玻璃的四条窄边绝热,两个正方形平面与空气换热。在XOY平面接受激光的辐照,没有其他热源。因此,热传导方程如下:

(1)

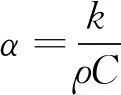
(2)

式中,a是光吸收系数;R是玻璃反射系数；P为激光总功率；激光束腰半径ω0。假设光束几乎不扩散,在材料表面的光斑半径也为ω0。

边界条件为:

(3)

因为目标关于z轴中心对称,因此只取空间中第一象限研究,式(3)中前两式表示目标在窄边绝热,并且在XOZ,YOZ面因为对称不会发生热交换；后两式表示目标在激光入射面和玻璃背面与空气发生对流换热,换热系数为H,假设两处换热系数相等。设初始温度T0为与时间无关的常数。

定解方程是关于空间和时间的二阶偏微分方程,利用积分变换法[8]可以将关于空间的二阶偏微分项去掉,变成容易求解的一阶偏微分方程。建立正、逆变换:

(4)

(5)

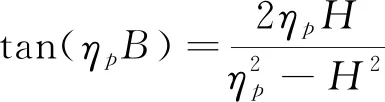
Z(ηp,z)=ηpcos(ηpz)+Hsin(ηpz),N(ηp)

(6)

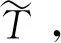
(7)

(8)

式中：

(9)

(10)

3 计算结果与规律分析

在计算和仿真中,对三种常用的光学窗口材料进行计算,其热物性参数如表1所示。光源选取波长1064 nm、总功率100 W的连续激光,光斑半径为1 mm,能量呈高斯分布(标准差σ=0.5),室温20 ℃。窗口材料设定为长50 mm、高50 mm、宽5 mm的平行平板。

表1 几种窗口材料的热物性参数

以K9玻璃为例,经过500 s激光辐照后,表面温度场趋于稳定,其分布如图2(a)所示。人由于光源是高斯光束,热平衡后的温度场也近似于高斯分布,如图2(b)所示。

图2 K9玻璃受幅照表面温度场分布及等温线

3.1 激光参数对温度场影响

该模型中,将激光的作用等效为一个能量密度随位置变化的体积热源,假设使用的是高斯激光,并且光在通过玻璃时逐渐被吸收,则体积热源的能量分布是沿Z轴逐渐衰减、在垂直于Z轴的任意截面呈正态分布。因此,研究激光参数变化对温度场的影响,只需要考虑激光参数对等效热源的影响即可。

根据解析式(8),某点温度正比于该点热源功率密度对于g时间t的积分,这意味着越大的激光功率P和越小的光斑半径r,能产生更高的温升,符合我们对激光辐射的常规认识,如图3所示。

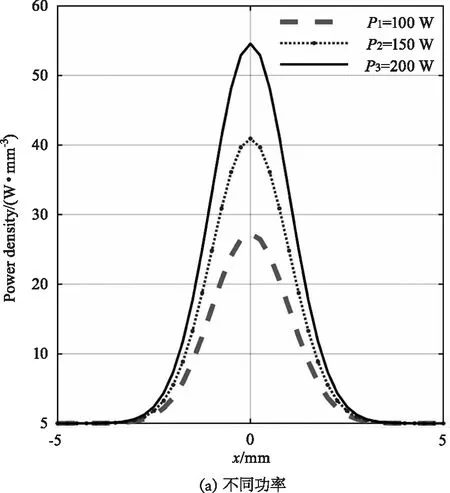
图3 不同参数下等效热源功率密度表面分布

对于激光光斑抖动、束散或漂移的情况,可以视作增大辐照光斑、降低能量密度进行处理。例如,采用蒙文等提出的光斑抖动模型[9],将半径2 mm、总功率100 W的激光光斑等效为抖动光斑,其半径和功率变为:

R′=0.6827Ltanθ+R

(11)

(12)

式中,R,R′指原光斑和等效光斑的半径；P,P′指原光束总功率和等效光束功率；L为光源到材料表面距离；θ为误差偏离角。假设距离为1 m,偏离角0.2 mrad,对等效热源密度的影响如图4所示。

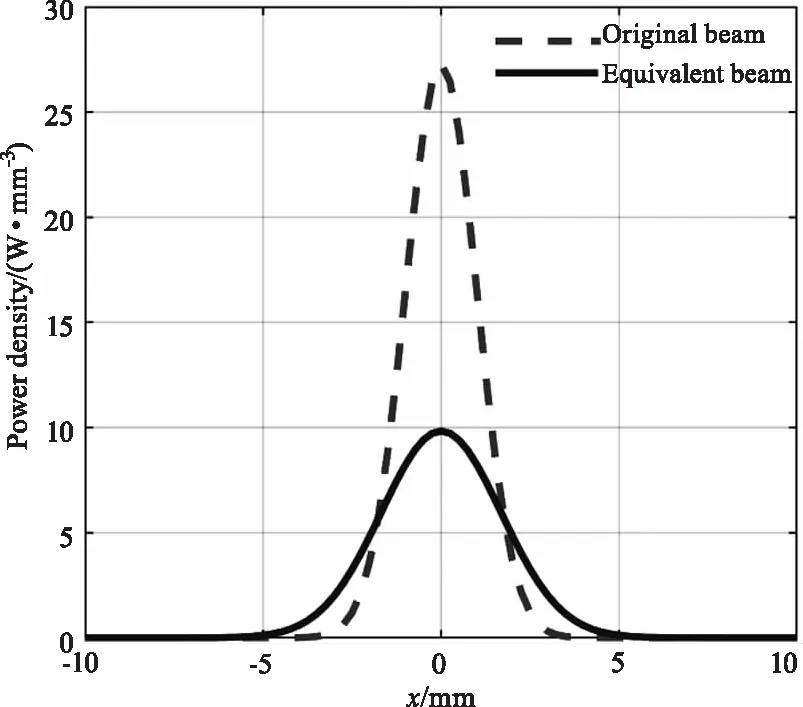
图4 引入光斑抖动前后的等效热源功率密度对比

3.2 材料参数对温度场影响

在激光参数不变的情况下,材料性质的差异显然是温度场差异的决定因素。由公式中分析可知,导热系数k,密度ρ,比热C,反射率R和体积尺寸等参数决定了某时刻的温度场数值。对于常见的三种光学窗口材料,整理了其热学性质,并在同种光源和不同光源情况下对其温度场进行了分析。

下面是几种常见的可见光和红外波段窗口材料激光辐照仿真的结果。可见长时间辐照后,材料整体温度分布与等效热源功率密度分布轮廓相似,且因为达到了热平衡,此时三种材料都没有达到熔融或软化点如图5所示。

图5 三种材料温度场仿真结果

(13)

当材料尺寸相同、辐照时间相同时,公式(13)中的特征值和积分时间是相同的；c是与时间无关的常数项。因此,可以看出目标材料的温升大致上与密度ρ、比热C和反射率R成负相关；与吸收系数a成正相关。

考虑到激光毁伤光学窗口材料的需求,理解吸收系数a对于温度场的影响十分必要,但是通过固定光源参数、改变材料的方法,不能考察吸收系数对温度场的独立影响,因为材料的其他参数例如密度、比热也改变了。吸收系数是相关于材料本身和光波长的属性,因此这里考察同种材料对应不同波长激光的温度场变化情况,就能分析吸收系数对温度场的影响。在反射率R接近于0,厚度为d,透射率为T时,可以认为:

(14)

因此,对于不同波段激光辐照的同种材料,其透过率和反射率越小,吸收系数越大,对应单位时间内辐照温升就越大。以K9玻璃在1.064 μm、1.3 μm、1.5 μm这三种光源下的温升情况为例,如图6所示。

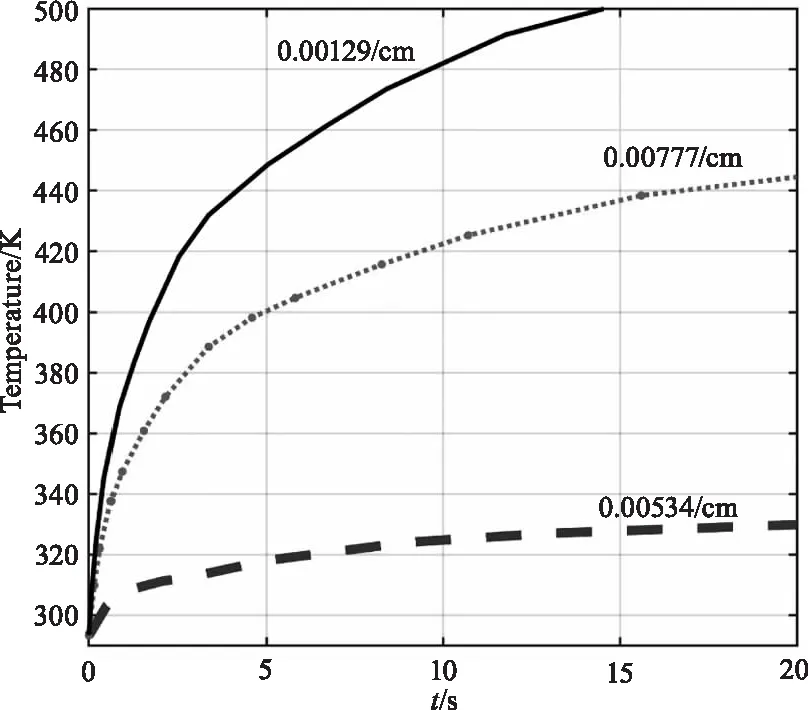
图6 不同吸收系数对K9玻璃辐照中心点温升的影响

由图可见,随着K9玻璃的光吸收系数增大,温度场上升速度大幅增加,并且换热情况下的热平衡温度也上升了。

3.3 边界换热系数对温度场影响

一些文献中,计算时将边界条件设置为绝热,虽然能得到形式简单的解,但是会造成一下错误:第一,材料温度随着辐照时间延长,可以无限上升；第二,沿光轴方向的温度基本相同。这是因为绝热条件下的模型不考虑与空气对流换热,只有热量输入没有输出,所以不会达到热平衡点；同时不考虑散热也影响了沿光轴方向的温升计算,使得温度在此方向变化很小。使用这样的模型会导致忽略温度上升限制,与实际情况不符的后果,并且计算热应力时也会受到影响。图7和图8是将边界条件设置为与空气换热,计算辐照1064 nm激光辐照500 s时,与同条件的绝热情况进行对比。

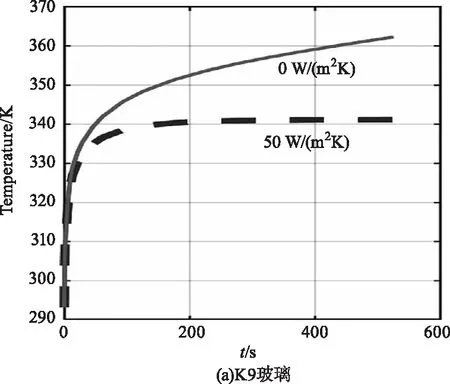
图7 换热与绝热条件下温升情况对比

图8 K9玻璃主光轴温度分布

由图可见,换热条件下温度升高到一定数值后达到稳定,不随辐照时间增加而上升,但是绝热条件下温度可以一直上升；换热条件下沿光轴方向的温度分布是中部高、两侧低,并且峰值靠近辐照面,这是由于两个边界正进行对流换热,并且等效热源在前表面能量密度大造成的。绝热条件下的光轴方向,温度相差不超过0.04 ℃,差异不大。

换热模型中,考虑模型达到热平衡时,材料温度不再上升,激光的能量输入与空气换热能量输出持平:

(15)

式中,S指换热表面面积,该模型中考虑入射面和出射面与空气换热,左式表示热平衡时的流出能量,右式表示流入能量。显然当激光参数不变时,右式为常数,因此平衡温度T与换热系数H成反比关系,即换热系数越大,热平衡时的温度越低,如图9所示。

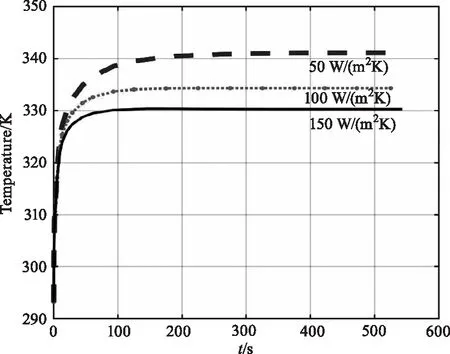
图9 不同换热系数下K9玻璃辐照中心温升情况

4 结 论

利用积分变换的方法,求解了包含换热条件的三维温度场模型,并对三种常用光学窗口材料进行计算和仿真。将激光光源参数转换为等效热源的属性,通过改变等效热源的参数可以计算温度场随波长、功率、光斑半径以及光斑抖动等影响的变化情况,分析了大激光功率和小光斑半径有利于产生更高的中心温度；对于不同材料,其密度、比热和反射率越小越利于温升,对应的光吸收系数越高,温升越快,热平衡温度也更高；对比了常见的绝热模型和本文的换热模型在热平衡情况和主光轴温度分布上的差异,材料实际上受辐照最终达到热平衡,且平衡温度与换热系数成反比、与光源能量成正比,本文建立的换热模型更符合实际。