基于VOF法毫秒激光制孔过程数值研究及工艺优化
2022-03-18夏海洋杨广峰
崔 静,刘 玲,夏海洋,杨广峰
(中国民航大学,天津 300300)
1 引 言
具有耐腐蚀等优点的钛合金已经大规模应用于航空发动机压气机叶片、结构部件上。作为发动机叶片重要组成部分的冷却孔可以降低叶片表面温度[1-2],冷却效果受冷却孔的加工精度影响,对加工精度要求高,激光打孔技术可以解决冷却孔深径比大、群孔加工难等问题。现有的实验研究无法获得加工过程相变演化机制和打孔的机理[3],而仿真方法可以获得激光打孔中的瞬态参数和相场演变过程,因此采用数值模拟对物理问题进行系统的研究成为一种必要的研究手段。
宋林森等[4]建立了二维激光打孔模型,分析了孔深、孔径与激光能量的关系,未考虑等离子体以及气液混合物向外喷射等因素;Park等[5]利用 VOF建立打孔模型研究了硅表面的激光打孔行为,忽略了打孔过程中的蒸发现象,只考虑材料的熔化及液体飞溅;褚庆臣等[6]建立二维激光打孔瞬态模型,比较不同参数下的孔型,为后期孔型的选择提供了依据,忽略了金属蒸汽对材料表面的辐射作用;杨俊华[7]建立了0Cr18Ni9不锈钢激光打孔的数值模型,得到了不同功率下的温度场分布图,未考虑材料表面对激光的反射作用、打孔结束后熔融物在孔壁重新凝固以及等离子体的作用;Yan等[8]忽略了孔中的激光束多次反射、等离子体的形成及其对材料的作用建立了二维轴对称激光有限元模型来研究熔融相界面尺寸和温度与飞溅物沉积量之间的关系;Zhang等[9]考虑了相变和蒸发建立了二维激光打孔模型,研究了激光参数对孔深和孔径的影响。
现有的研究主要模拟二维激光打孔的温度场,未考虑蒸发过程的反冲压力、重力、粘滞力一起作用时对激光打孔的影响。本文以钛合金TC4为研究对象,基于VOF法构建了三维激光打孔模型。模型中考虑了重力、反冲压力、粘滞力和熔融潜热以及固-液-气三相的相变过程;模拟了激光打孔过程中孔的温度场、相场以及孔型的演化,得到了孔径、孔深以及飞溅物的变化,并将数值分析与实验的结果进行了对比,为实际工艺提供完整的热场、相场信息。
2 物理问题/模型
毫秒脉冲激光打孔的物理模型如图1所示,从激光器发射出来的激光束辐射到TC4表面,辐射的部分快速升温并气化,呈现气-液-固三相共存的状态,反冲击压力把熔融金属带出孔外之后,下一个脉冲作用时直接辐射孔底,并一直重复上述过程,直到击穿孔。
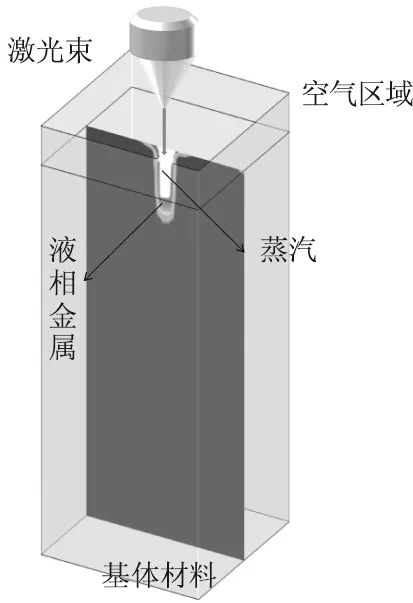
图1 毫秒脉冲激光打孔的物理模型
为了简化激光打孔过程,假设条件如下:
(1)激光光束呈平顶分布,光源垂直入射;
(2)基体为100 %光滑、各向同性、质地均匀的材料,材料的尺寸远大于光斑尺寸。
3 数学模型
根据上述假设,结合激光打孔的实际情况及提升打孔精确度,描述激光打孔过程的控制方程包括体积分数控制方程、质量守恒方程、动量守恒方程、能量守恒方程、湍流控制方程。
3.1 VOF相体积分数模型
基于VOF法,基体的固体相、熔化的液相、蒸发的气相,这三相之间没有交界面,通过求解每相的体积分数来追踪气液固界面的位置,其演化方程为:
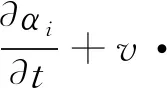
(1)
式中,αi表示i相的体积分数;v为流体速度;Sαi为体积分数源项。其中αi的表达式为:当αi=0时,表示网格单元不存在i相;当αi=1时,表示网格单元中只有i相;当0<αi<1时,表示网格单元中包含了i相和其他相共存。主相体积比率的计算基于如下的约束:
αs+αl+αg=1
(2)
式中,αs,αl,αg分别为固相、液相、气相体积分数。
3.2 质量守恒方程
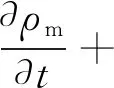
(3)
式中,ρm为混合密度;vm为混合速度。
(4)
(5)
式中,ρi为i相的密度;vi为i相的速度。
3.3 动量方程
(6)
式中,p为压力;Su为动量源项,其反冲压力大小F表示为:
(7)
式中,Tv为蒸发温度;kb为玻尔兹曼常数;Lv为蒸发汽化潜热;T为基体材料的温度。
3.4 湍流流动方程
在激光打孔成型的过程中,材料在激光的高温作用使液相金属在反冲击压力的作用下形成飞溅物,飞溅物在孔径内会阻碍流体流动,加速湍流的出现。本文使用标准k-ε模型来模拟流体流动。
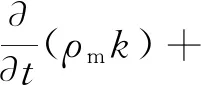
Gk,m-ρmε+Sk
(8)
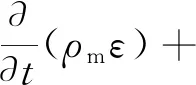
(9)
式中,k为湍动能;Gb为浮力产生的湍动能;ε为耗散率,C1ε=1.44;C2ε=1.92;C3ε=0;σε=1.3;σκ=1.0;μt,m为湍流粘度,μt,m=0.09ρκ2/ε;μm为三相混合物平均粘度,μm=αsμs+αlμl+αgμg。
Gk,m为紊流动能的产生,其表达式为:
Gk,m=μt,m(∇vm+(∇vm)T):∇vm
(10)
3.5 能量守恒方程
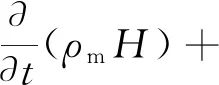
(11)
焓H是以混合焓形式出现:
H=h+ΔH
(12)
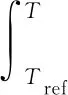
(13)
式中,href为参考焓值;Tref为参考温度;cm为糊状区域材料的比热容。
相变潜热与液相质量分数、液相质量分数与温度的关系可用下式表示:
(14)
式中,Li为i相的相变潜热。
3.6 源 相
3.6.1 液相体积分数源项
(15)
式中,Sαl为液相体积分数源项;Tsus为固相线温度;Tlus为液相线温度。
蒸发过程的蒸发率:
(16)
式中,M为金属材料的原子质量;β为凝结系数。
3.6.2 动量方程源项
(17)
式中,ξ为一个小数,其值为0.001;Amush是糊状区常数;vp为固体材料从区域中拉出而产生的固体速度。
3.6.3 能量方程源项
(18)
式中,P为激光输出的总功率(kW);r为激光束的光斑半径(m)。
3.6.4 湍流源项
(19)
(20)
4 离散化处理
模型中建立的尺寸为2 mm×2 mm×5.5 mm的三维网格,如图2所示。采用的是非均匀六边形网格,越靠近空气与基体的交界面的网格越密,离交界面越远的区域的网格越稀疏,计算的单元数为650000个,时间步长为0.00001 s,材料的物性参数见表1。
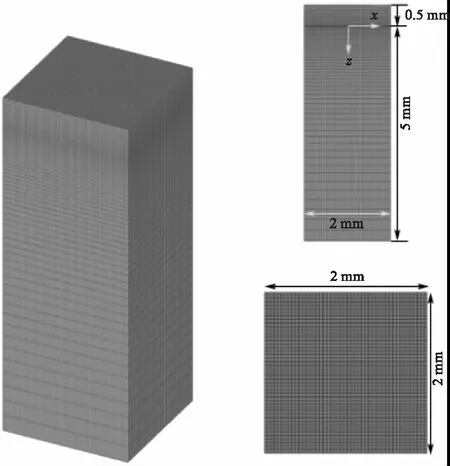
图2 激光打孔有限元模型网格划分
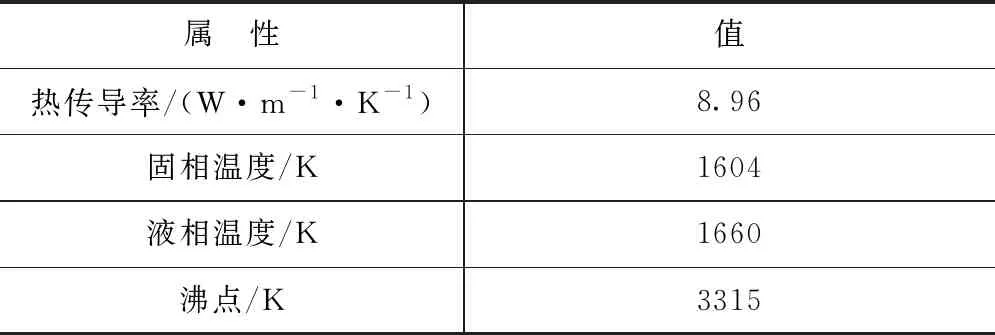
表1 TC4合金物性参数
5 模型求解
5.1 网格无关化验证
本文分别采用15×30×100、15×40×100、15×50×100、20×55×100的网格,对工况1(脉冲宽度为1.0 ms,激光能量为9 J,光斑直径为0.1 mm)开展了数值研究,表2中给出了不同网格数下获得孔深,计算结果相差不大,本文后续模拟均采用15×50×100的网格。

表2 不同网格下的孔深
5.2 模拟工况
本文选取了脉冲个数进行研究,不同激光工艺参数如表3所示。

表3 激光工艺参数
6 模拟结果分析
图3(a)显示了不同脉冲个数下的温度场的变化趋势,第一个脉冲作用结束后,材料表面迅速升温,形成深而窄的温度场;虚线的温度升高到3300 K以上,已超过了材料的沸点,这一部分金属将发生熔化、汽化形成金属蒸汽对孔内熔融金属产生了反冲击作用力[10],熔融金属喷射到空气中遇冷形成飞溅物,从而实现材料的去除。当第二个脉冲作用时(图3(b1)),能量直接作用于孔底,热量沿轴向传递的速度增加,随着脉冲个数递增,高温区逐渐变深,表示孔周围的温度达到1700 K以上,表示孔周围有着一层细薄的熔体,由图3(a1)~(d1)可知孔底的熔体在逐渐增多,即增大脉冲个数,孔底的热量更多。随着脉冲作用连续,逐渐形成以光束轴线为中心的温度大于两侧的温度分布状态。
图3(b)表示不同脉冲个数下气相体积分数的演变过程,不同灰度部分分别表示材料的固体、气体、液体状态,三者交界处是气-液-固界面。由图3(a2)~(f2)可知,交界面发生了下移,是因为金属蒸汽在带出一部分熔融金属的过程中,向周围传递了热量,促使熔池凹陷,因此交界面发生下移。图3(b2)灰色箭头是熔池在流动过程中所形成的峰谷结构,这说明湍流在影响熔融层的流动,随着脉冲作用,这种结构逐渐减小,这可能是影响孔质量形成的机制之一[11]。

图3 激光打孔的温度场、气相体积分数与脉冲个数的关系
如图4(a1)、(a2)第一个脉冲作用完后,打孔作用较明显,开始去除材料,形成一个宽约0.336 mm,深约0.596 mm的光滑凹坑,孔深、孔径在脉冲分层汽化作用下逐渐增加,最终在图4(f2)形成入口孔径为0.443 mm、出口孔径为0.315 mm的类似“杠铃”的孔型;如图4(b2)~(e2)所示,灰色箭头所指部位为孔壁上有些许不规则小凹坑,图4(f2)时孔壁内没有小凹坑且光滑;如图4(a1)~(d1)所示,相同时间下,小孔的深度从0.596 mm到1.981 mm,这说明打孔的速度在逐渐增加。孔深较小时,激光光斑靠近材料表面,作用范围扩大,沿径向的材料相对容易达到汽化温度[12],且激光能量集中在孔底,底部均匀受热,能够较好的维持底部孔径,由于脉冲的迁移,小孔周围能量的集中导致温度逐渐提高,材料熔化的部分增多,所以打孔速度逐渐增加;随着小孔深度的增加,孔内的蒸汽也在逐渐增多,对孔的底部产生了反冲击压力,推动着金属向四周流动,在脉冲占空比的影响下,所以从第二个脉冲开始中间有了小凹坑,第六个脉冲如图4(f2)所示,金属蒸汽在反冲压力和重力的相互作用下,推动着熔融金属流动,使小凹坑去除。
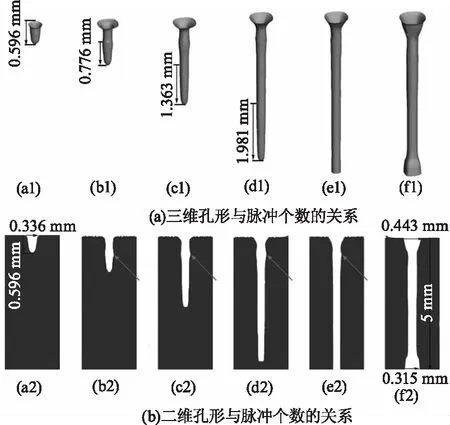
图4 激光打孔时孔形随脉冲个数的变化(三维、二维)
图5显示随着脉冲个数的增加,最小孔径的大小变化较慢且不明显;最大孔径、平均孔径以及孔深都随着脉冲数量的增加而增大;由图5可知,打孔初始,最大孔径增加的速度大于孔深的增加速度;第二个脉冲个数后,孔深的增加速度大于最大孔径的增加速度;在第五个脉冲时已经击穿孔。第一个脉冲作用时产生的蒸汽带走部分熔融金属,下一个脉冲直接作用于孔底,大部分热量在基体厚度方向传递,孔深的增加速度在第一个脉冲到第四个脉冲逐渐增加,直到打穿;最大孔径增长速度前后不一样的原因是靠近光斑中心的材料容易汽化,离中心越远的区域达到汽化温度的时间越迟。打孔初期,横向材料的去除率更高,随着激光的持续作用,孔壁离激光中心有一定的距离,孔径在后期缓慢增加。
图6显示随着脉冲个数的增加,深径比也在逐渐增加,当脉冲个数为4时,深径比突然缓慢增加,这是因为深径比不仅与孔径有关系,还与孔深有关系,由图5可知,在第五个脉冲时,孔已经击穿,所以在孔深一样的情况下,最小孔径的增加使第六个脉冲的深径比第五个的小。
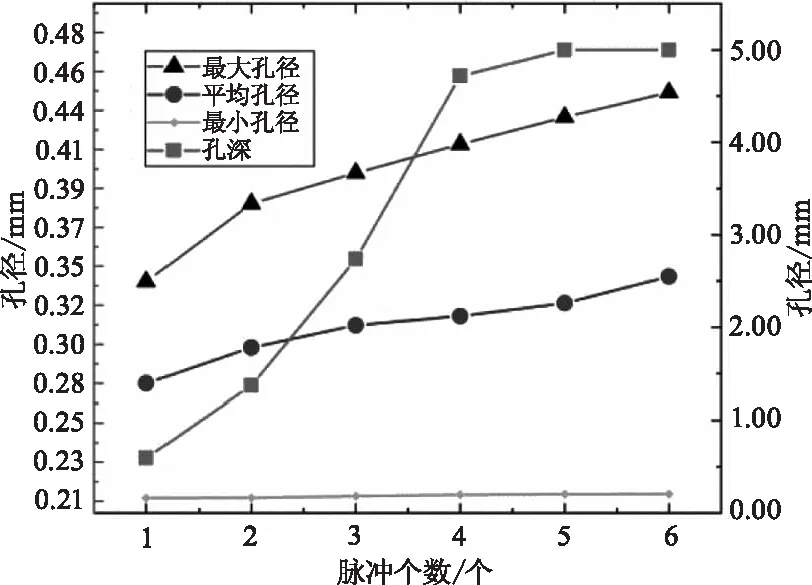
图5 激光打孔的最大(小)直径、孔深、平均直径随脉冲个数的变化趋势
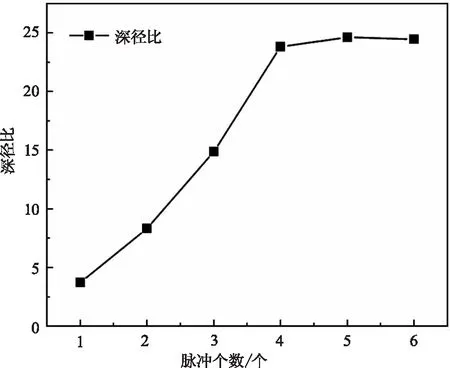
图6 深径比与脉冲个数的关系曲线
由图7可知飞溅物随着脉冲数量的增加而增加,从图7(a2)~(f2)中可知里面是圆孔外面形似银色的椭圆层包围着,随着脉冲个数的增加,外面包围着的飞溅物在一点点的增大,直到全部包围变成椭圆形。从图7(b)中可知随着脉冲的持续作用,飞溅物的最大高度在持续增加;箭头所在的飞溅物的高度明显线性减少,直至减为0;在0点处飞溅物的高度明显有凹陷下去的趋势。

图7 激光脉冲个数作用下飞溅物的俯视图、主视图以及其放大图
由图8知从第一个脉冲到第四个脉冲,在每个脉冲作用下,飞溅物的高度均增加了0.021 mm,从第四个脉冲到第五个脉冲,飞溅物的最大高度增加了0.013 mm,最终飞溅物所达到的最大高度为0.1005 mm;飞溅物的体积随着脉冲个数的增加而增加,但其增加的速度却在逐渐减慢,最终飞溅物的体积为0.0363 mm3。这是因为:孔内的金属蒸汽压力并不会把熔融金属全部带出去,会有部分残留在孔壁,当最后击穿孔的时候,一部分由于反冲压力喷射出去,另一部分由于重力作用从孔底流出,所以后期飞溅物的增长速度减慢。
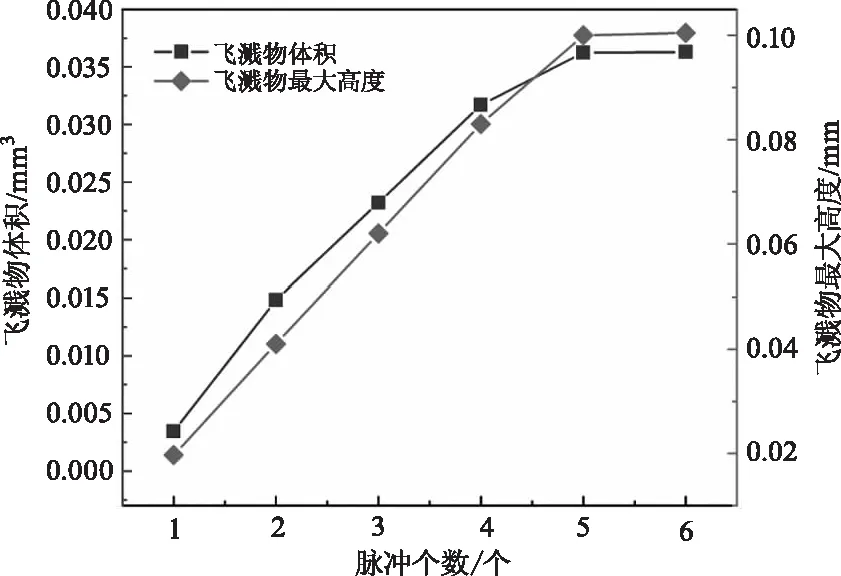
图8 飞溅物的最大高度、体积与脉冲个数的关系
7 数值模拟与实验论证
为了进一步验证数值仿真的结果的准确性,将相同参数下实验轮廓与模拟轮廓进行对比,结果如图9所示,模拟与实际打孔的孔型均为对称结构,由于受到实际条件的影响,实际打孔的底部孔径比模拟的孔径小,使得横截面呈类圆锥形。从图9可知,孔深和孔径的数值基本一致,在实验误差允许的范围内,仿真与实验结果基本吻合,说明数值模型的合理性。
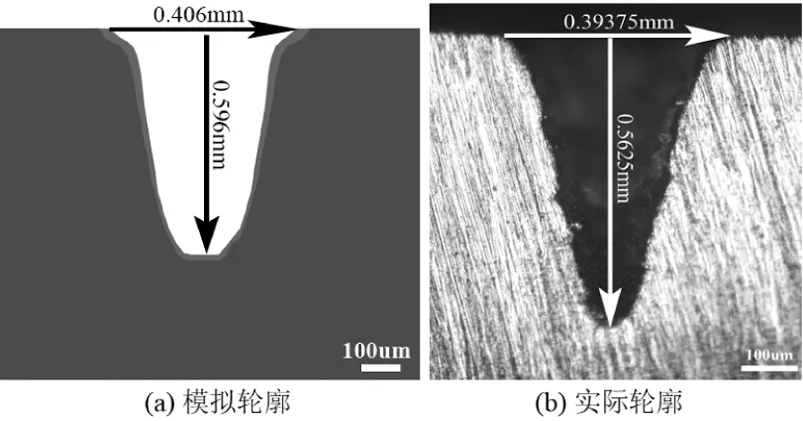
图9 孔轮廓的数值模拟与实验结果对比
8 结 论
(1)激光垂直照射材料时,高温区向材料厚度方向移动,形成以光束轴线为中心的温度大于两侧的温度分布状态,在孔的周围有一层温度为1700 K以上细薄的熔体。气-固-液交界面随着脉冲的作用逐渐下移。在脉冲间歇性和反冲压力的作用下,孔形中出现了峰谷结构,随着脉冲数量增加,峰谷结构逐渐被消除。
(2)脉冲数量的增加使得最大孔径、平均孔径都在变大,最大孔径增加速度前后不一致,最小孔径变化速度较慢,入口孔径和出口孔径都在变大。飞溅物的最大高度、体积随着脉冲数量的增加而增加,从俯视图中可以看到飞溅物的形成过程:由圆孔外面包围着银色的锯齿状的飞溅物逐渐变成椭圆型。
