相互逼近技术用于小行星702(Alauda)的高精度位置测量试验 *

覃永贵，彭青玉

(1. 暨南大学计算机科学系，广东 广州 510632；2. 暨南大学中法天体测量、动力学与空间科学联合实验室，广东 广州 510632)

目前，大部分小行星的位置测量是基于地面光学望远镜观测的图像资料，因而提高地面观测的测量精度是一项十分重要的工作。然而，影响小行星测量精度的主要因素有两个：(1)即使在短曝光条件下，快速运动的小行星在电荷耦合器件(Charge-Coupled Device, CCD)上成像仍存在拖影，从而引起测量精度的损失。为了解决此问题，文[1]提出了合成追踪技术以获取准确的近地小行星位置。随后，文[2]利用该技术得到近地小行星位置测量的精度为10毫角秒。(2)星表提供恒星数据的精度问题。由于星光在进入地球大气层后发生抖动，历史上的星表在恒星位置或自行上精确度不高，给观测对象的位置测量带来了不可忽略的误差。随着航空航天技术的发展进步，人们把探测器发射到空间，以消除地球大气的影响。欧洲空间局成功发射了盖亚卫星，在完成阶段性测量任务后发布了盖亚星表，为高精度的天体测量工作奠定了重要基础。盖亚星表由于其恒星参考星数量庞大及精度高的特性[3-4]，在位置归算工作中得到国际同行的广泛认可。

2016年，文[5-7]基于两天体相对位置测量存在精度回报[8]提出了相互逼近的天体测量技术，可以精确测量两颗天然卫星的相对距离，并成功地将该技术应用到木星伽利略卫星的天体测量。2019年，文[9]使用该技术对天王星的卫星进行了天体测量，参考喷气推进实验室(Jet Propulsion Laboratory, JPL)历表，测量结果显示，伽利略卫星内部精度达到11.3毫角秒，天王星卫星达到45毫角秒，并且伽利略卫星间测量结果在准确度和精度上均与联合天象技术相媲美。2019年，文[10]基于M35星团进一步研究了精度回报现象，发现相距100″以内两颗天体之间的相对位置测量存在精度回报，并且可以使用Sigmoid函数描述这两颗天体之间的精度回报特性。这项工作为CCD图像上任意两个天体之间的相对位置测量精度提供了定量描述。理论上，无论两个天体是否存在相对运动，都有精度回报现象。

本文把相互逼近技术从两颗天然卫星天体拓展到小行星和邻近恒星参考星(位置参考盖亚星表)的相对位置测量，并利用该技术改善小行星的位置测量精度。

1 相互逼近技术

1.1 理论模型

如图1，假设小行星做匀加速直线运动(加速度为a)经过该天空平面(100″以内)，在小行星经过的路径附近，存在一颗参考星Ref。在观测时间内，小行星从A点运动到B点，并令小行星在A点的时刻t=0(即起始点)。小行星到达C点时与参考星的角距离达到最小值(即冲击参数，用d0表示)，到达C点的时刻称为中心时刻(用t0表示)。对于观测时间内的任意时刻t，小行星和参考星的角距离为d(如图1中的B点)。显然，角距离的平方

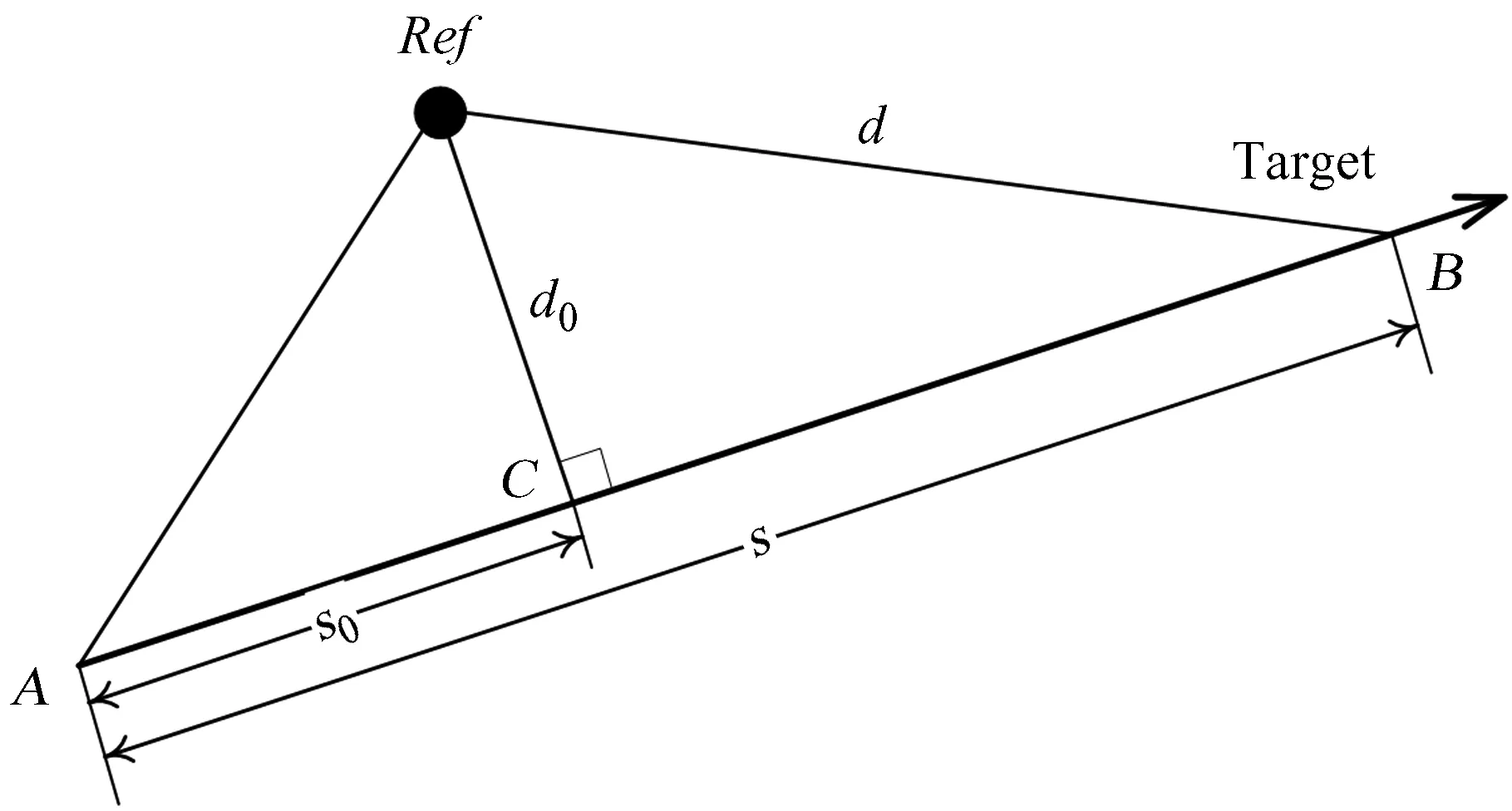
图1 小行星与参考星的相互逼近模型

(1)

其中，v为小行星在t=0时的速度。我们使用最小二乘法求解(1)式的系数(a0～a4)，且

(2)

对(1)式求一阶导数并令其等于0，中心时刻t0就是

(3)

的根。我们可以通过迭代求解(3)式的根，得到中心时刻t0的值。令t=t-t0，使中心时刻t0=0，之后重新拟合(1)式，这时(1)式中的参数s0和t0均为0，于是有

(4)

由(4)式可知，当使用中心时刻t0=0的观测数据再次拟合(1)式后，可以通过(4)式直接求解冲击参数d0和小行星在中心时刻t0的速度v(即小行星运动到图1中C点的速度)。

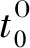
1.2 Δd和Δs的投影

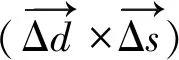
图2 Δd和Δs投影到赤经、赤纬方向

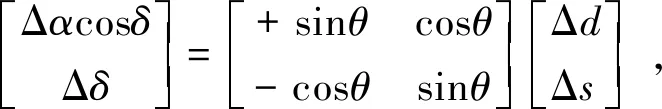
(5)

否则，

(6)

1.3 比例尺

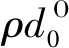
2 数据归算与结果分析

2.1 观测资料

2020年11月11～12日，我们使用中国科学院云南天文台1 m光学望远镜(I滤光片)对小行星702(Alauda)进行了观测，观测所用望远镜和CCD的参数见表1。两晚共获得550帧图像数据，每晚拍摄的图像数量、曝光时间和相互逼近事件的数量见表2。此外，使用I滤光片进行观测可以有效减小较差色差折射(Differential Colour Refraction)效应对天体测量的影响[14]。

表1 1 m光学望远镜和CCD参数说明

表2 小行星702(Alauda)的观测资料概要Table 2 Observations overview for asteroid 702 (Alauda)

2.2 数据归算

在对参考星的位置测量和归算中，我们参考欧洲空间局发布的Gaia DR2星表[3-4]，小行星702(Alauda)的理论位置参考美国国家航空航天局喷气推进实验室发布的历表(https://ssd.jpl.nasa.gov)。在位置归算中，我们均考虑站心视位置和大气折射的影响。

小行星与参考星相互逼近的归算步骤：(1)对所有的观测资料使用二维高斯定心算法拟合求解参考星和小行星在图像中的像素位置；(2)计算小行星和参考星之间像素距离的平方，并用于拟合4次多项式函数(即(1)式)；(3)对拟合得到的(1)式进行一阶求导，并令其等于0(即方程(3))，迭代求解(3)式的根，获取中心时刻；(4)将观测数据的时间减去中心时刻，再次使用观测数据拟合(1)式。根据(4)式，计算冲击参数和小行星在中心时刻的速度。同理，小行星和参考星的理论数据也进行上述类似的归算过程。于是，我们得到小行星在中心时刻的位置偏差，即Δd和Δs。利用JPL历表，计算小行星的速度方向与赤经方向的夹角θ，根据1.2节的方法，将Δd和Δs投影到赤经、赤纬方向，最后得到小行星的测量位置在赤经、赤纬两个方向观测值与理论值之差。

2.3 结果与分析

在2020年11月11～12日的观测资料中，分别存在2颗和3颗参考星与小行星702(Alauda)相互逼近，归算结果见表3。目标小行星702(Alauda)在JPL历表中的星等约为12 mag，5颗参考星的G星等范围为13～16 mag，小行星和参考星的星等差不大于5。比较相互逼近测量技术与经典天体测量的归算结果(见表3)可以得出，两者位置测量的观测值与理论值之差的平均值在赤经和赤纬方向有良好的一致性，前者的精度分别为6毫角秒和2毫角秒，相比后者有6～10倍的提高。此外，虽然使用更高阶模型的经典天体测量可以提高测量精度，但是我们在使用相互逼近技术时，并未考虑视场的扭曲和高阶大气折射模型，因而经典天体测量与相互逼近技术测量方法等价。

图3显示了表3观测资料的归算结果在赤经、赤纬方向观测值与理论值之差与参考星星等和冲击参数的关系。从图3可以看出，在赤经、赤纬方向，观测值与理论值之差与冲击参数没有明显的相关性；在赤经方向观测值与理论值之差与参考星星等没有明显关系，但在赤纬方向观测值与理论值之差与参考星星等之间可能存在二次函数关系。

2.4 误差分析

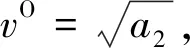
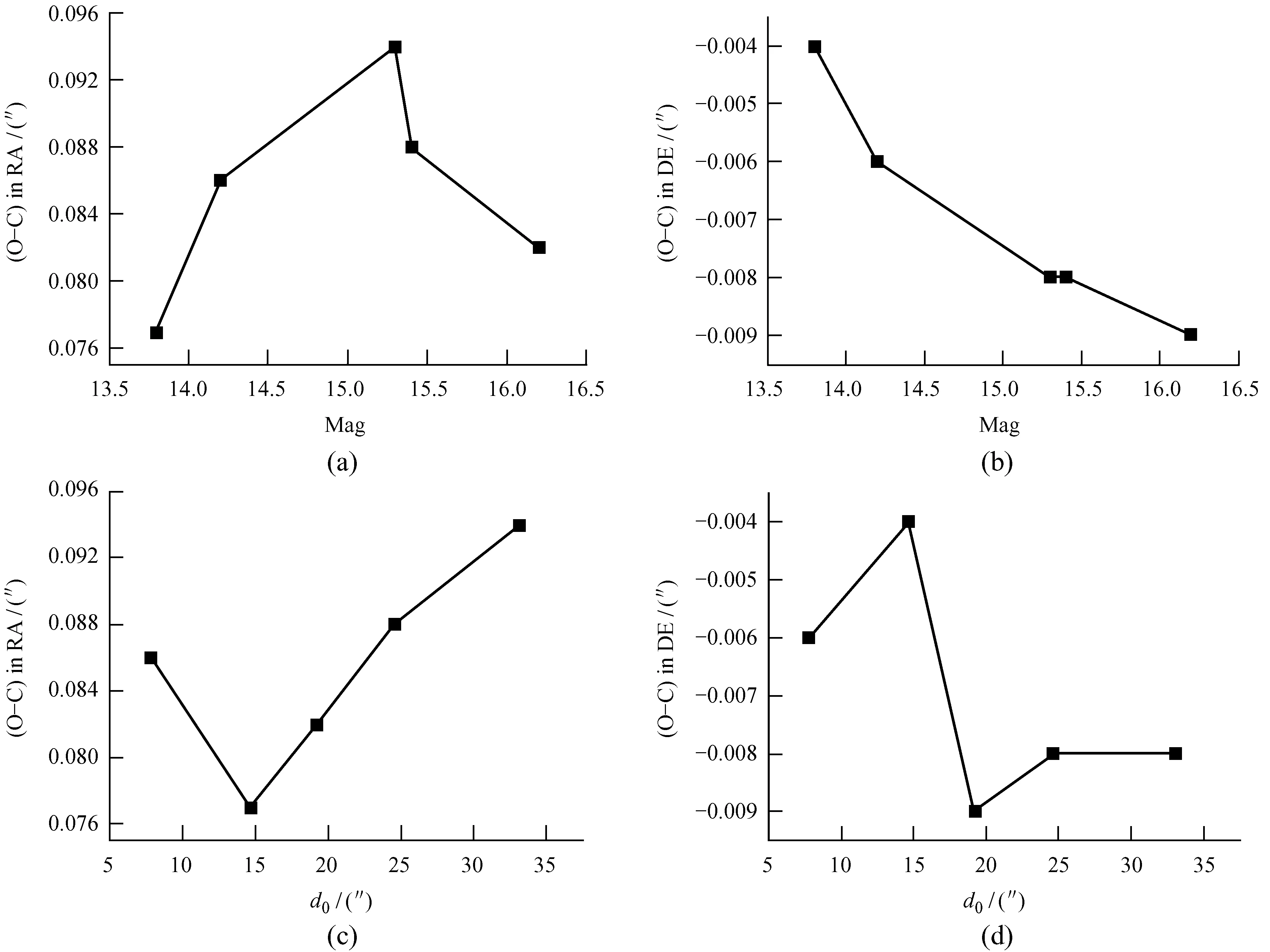
图3 观测值与理论值之差与参考星星等和冲击参数的关系。(a)和(b)分别表示在赤经、赤纬方向观测值与理论值之差与参考星星等的关系，(c)和(d)分别表示在赤经、赤纬方向观测值与理论值之差与冲击参数的关系

在对运动的天体进行高精度位置测量时，我们还需要考虑相位角效应等因素对测量结果的影响。根据文[15]，相位角影响的大小可以使用公式

(7)

描述，其中，r为目标的视半径；i为太阳相位角；Q为日下点在切平面的位置角；C为光照反射模型，且0≤C≤1， 又0≤|sinQ|, |cosQ|, |sin (i/2)|≤1。从JPL历表查询小行星702(Alauda)的视半径r在观测时间内的变化不超过0.04毫角秒，据此预估相位角效应对位置测量精度的影响不超过0.04毫角秒，远小于位置的测量精度，因此，相位角对本文归算结果的影响甚微。此外，当曝光时间较长时，运动速度较快的小行星受抖动效应影响，在CCD上成像存在拖尾现象，对小行星的高精度测量带来不可忽视的影响[2]。由于小行星702(Alauda)的运动速度较小(约0.006″/s)且曝光时间较短(30 s)，曝光时间与小行星运动速度之积远小于宁静度(约1.5～2.0″)，故抖动效应的影响可以忽略不计。

3 总 结

本文把相互逼近技术拓展到小行星和邻近恒星参考星的相对位置测量。不同于文[5-7]提出的相互逼近模型，本文的相互逼近模型是小行星和盖亚参考星之间相对位置测量的模型。此外，本文根据小行星在较小天空平面内作匀加速直线运动的假设推导相互逼近模型，不仅具有明确的物理意义，还能直接求解小行星在中心时刻的速度和冲击参数，在一定程度上优化了相互逼近模型。在使用1 m光学望远镜观测小行星702(Alauda)的资料中，我们一共捕获了5次小行星与恒星相互逼近事件。参考Gaia DR2星表的归算结果显示，相互逼近测量技术与经典天体测量相比，在赤经、赤纬方向有良好的一致性，相互逼近技术在赤经、赤纬方向的位置测量精度分别为6毫角秒和2毫角秒，比经典天体测量提高了6～10倍。上述结果表明，本文为小行星的位置测量提供了一种高精度的测量方法。

致谢：感谢中国科学院云南天文台1 m望远镜运行团组的帮助和支持，感谢郭碧峰、林孚荣在论文写作中给予的帮助。