大口径射电望远镜轮轨滚动接触有限元分析 *

师洪强，许 谦，王 娜，王兆军

(1. 新疆大学物理科学与技术学院，新疆 乌鲁木齐 830046；2. 中国科学院新疆天文台，新疆 乌鲁木齐 830011；3. 中国科学院射电天文重点实验室，江苏 南京 210033；4. 新疆射电天体物理重点实验室，新疆 乌鲁木齐 830011)

中小口径精度要求不高的射电望远镜普遍采用拼接轨道技术，拼接轨道在滚轮经过接缝时易出现跳动以及应力集中，从而影响天线指向精度和轨道使用寿命[1]。目前大口径、高精度射电望远镜轨道逐渐采用整体焊接技术，如美国绿岸射电望远镜(Green Bank Telescope, GBT)[2]、上海天马65 m[3]射电望远镜等。正在建设的新疆110 m口径全向可动射电望远镜[4]，方位轨道采用整体焊接技术，由于采用窄槽坡口焊接技术，因此堆焊层需要用到3种不同的焊接材料[5]。焊接过程中高温引起材料内部结构性能变化，造成焊缝位置硬度和强度与母材的差异。由于轮轨接触力分布有大载荷、小集中的特点，天线滚轮在经过焊缝位置时，焊缝与母材的差异可能引起轮轨接触力的突变。应力突变是引起疲劳磨损的主要原因之一，因此弄清滚轮经过焊缝时的应力变化尤为重要。

对于大型射电望远镜轨道而言，传统试验研究成本高昂，因此本文采用仿真分析的方法进行研究[6]。文[7]针对大型反射面天线轮轨接触问题，在不同仿真软件中进行对比分析，获得轮轨接触应力，但未涉及瞬态分析。文[8]通过三维有限元分析，用移动载荷法模拟轮子滚动，分析绿岸射电望远镜斜接缝轨道的力学行为以及耐磨板、基板接触界面的微动磨损，分析结果为轨道重新设计与改造提供参考。移动载荷法不能还原真实的轮轨接触状态，且材料差异带来的影响很难考虑在内。因此，需要采用完整的有限元模型才能更加真实、准确地反映轮轨接触的瞬态响应。

本文采用有限元法将天线轨道焊缝真实焊接工艺考虑在内，建立110 m口径全向可动射电望远镜轮轨接触模型，使用层级细分技术对模型进行相应处理。在此基础上采用 “面-面” 赫兹(Hertz)接触算法求解接触耦合，进而通过显式时间积分法获得轮轨间作用力在不同摩擦系数和轨道面形貌时的瞬态响应。研究结果可以为天线轨道的疲劳寿命分析和天线维护提供参考。

1 轮轨接触应力计算

本文建立的大型射电望远镜轮轨接触模型，由于接触斑的几何尺寸远小于轮轨几何特征尺寸，且不考虑天线滚轮的侧滑和蠕滑现象。因此，轮轨间作用力可以使用赫兹接触理论计算[9]，通过理论计算与仿真结果进行对比，验证模型的准确性，为瞬态分析奠定基础。

根据赫兹接触理论有关弹性体接触斑的几何尺寸关系，轮轨之间的接触可以看作是两个任意曲面弹性体的接触，接触斑呈椭圆形，长轴半径a和短轴半径b分别为

(1)

其中，N为轮轨间的法向力；m和n是与(B-A)/(A+B)有关的系数，引入记号

(2)

m，n和θ的关系可以通过查表获得；k1和k2为材料参数，可以表示为

(3)

E1，E2和ν1，ν2分别为滚轮和轨道材料的弹性模量和泊松比；轮轨接触曲面初始间隙函数的常数A和B可由

(4)

确定，其中，R11，R12，R21和R22分别为两个接触体的主曲率半径。求得接触斑长短半轴a，b之后，接触斑的内应力分布表示为

(5)

由(5)式可知，最大接触压应力q0出现在接触斑中心处，大小为

(6)

由于接触位置多为压应力，轨道一般不会因此损坏，而如果剪应力超过容许值，轨道内部发生塑性流动，容易引起钢轨的损坏。最大剪应力发生在轮轨接触面以下的某一深度，其值约为

(7)

接触面上的最大剪应力为

2τ1=n0q0，

(8)

其中，m0，n0与两接触体的主曲率半径有关，均可由查表得到[10]。通过以上公式即可计算天线轮轨接触力的大小和分布。

2 轮轨接触模型构建

2.1 模型建立

基于110 m口径全向可动射电望远镜建立仿真模型，天线座架共有4组滚轮，每组8个。取一个滚轮和两段轨道组成分析模型，如图1。轨道建模时考虑焊接过渡层、填充层及表面焊接层。滚轮轴采用三维线性有限元应变梁单元表示，并使用多点约束单元将轮轴与天线滚轮进行耦合，不仅可以将整个天线载荷均匀施加在滚轮上，也可以实现滚轮的滚动，有效简化了模型，又不失准确性。

有限元模型的计算准确性高度依赖于网格划分精度，当接触斑区域网格尺寸为接触斑短半轴宽度的1/20时，可以得到精确的轮轨接触解，当网格尺寸为1/10时，可以满足大多数工程问题的精度要求[11]。采用层级网格细分技术，对焊缝附近区域的轨道及滚轮进行网格细化，最小网格尺寸为1.1 mm。如图1，模型采用8节点6面体单元进行离散，焊缝位置采用共节点方式，以减少接触设置，提高计算效率。为了保证网格质量，所有网格的长宽比小于3.5，最终整个模型网格数量约79万，节点数82万，其中焊缝附近网格数量约占总体网格数量的91%。

图1 模型及网格Fig.1 The model and grid

轨道材料为高质合金钢42CrMo，而焊缝位置表面需要较大硬度以保证其耐磨性和使用寿命，因此，焊接坡口需要一层较软的材料作为过渡，将轨道材料与表面堆焊层进行有效衔接。过渡层厚度约4 mm，由于目前有限元分析无法实现对材料硬度的表征，因此本文通过采用不同的弹性模量近似表征不同焊接工艺的熔敷金属硬度。文[12]通过实验分析指出，越靠近焊缝位置，材料弹性模量越小，焊缝中心位置弹性模量最小，约为母材的90%。因此取过渡层及填充层的弹性模量约为轨道的90%，表面堆焊层约为轨道的95%。材料具体参数如表1。

2.2 载荷与工况设置

考虑到天线的重量以及轨道的合理承载，将单轮载荷设为2 × 105kg，保证实际工况的安全性。在轮轴上施加集中载荷，考虑轨道自重影响，其底面设置为全约束，滚轮约束横向自由度以避免横向滑移。

工况1：当滚动速度为20 mm·s-1，摩擦系数分别为0.3，0.4和0.5时，分析当天线滚轮经过焊缝时，轮轨间作用力的瞬态响应。

工况2：当滚动速度为20 mm·s-1，摩擦系数为0.3，分析焊缝表面不平度分别为0.1 mm，0.2 mm和0.3 mm时，对轮轨间作用力的影响。

表1 材料参数Table 1 Material parameter

瞬态分析时，设定滚轮和轨道接触起始位置与焊缝轨道交界线之间为稳态过渡区，以保证滚轮进入焊缝区时初始激扰的能量被消耗[13]。通过计算，稳态过渡区取值为70 mm。

2.3 时间步长确定

时间步长与数值分析误差分布有关，合理的时间步长可以保证数值分析稳定性和计算精度。确定时间步长不能以一次计算结果为准，应该对比3个相距一定时间间隔步长时的计算结果，若相对偏差较小，即可取中间步长的计算结果作为问题的合理解[14]。取3个时间步长分别计算2 s内滚轮经过相同位移时，绘制轨道上同一位置的应力时变曲线，如图2。从图2可以看出，不同时间步长对分析结果影响较小，因此选取时间步长为0.025 s进行瞬态分析。

3 轮轨接触有限元分析

3.1 静力学分析

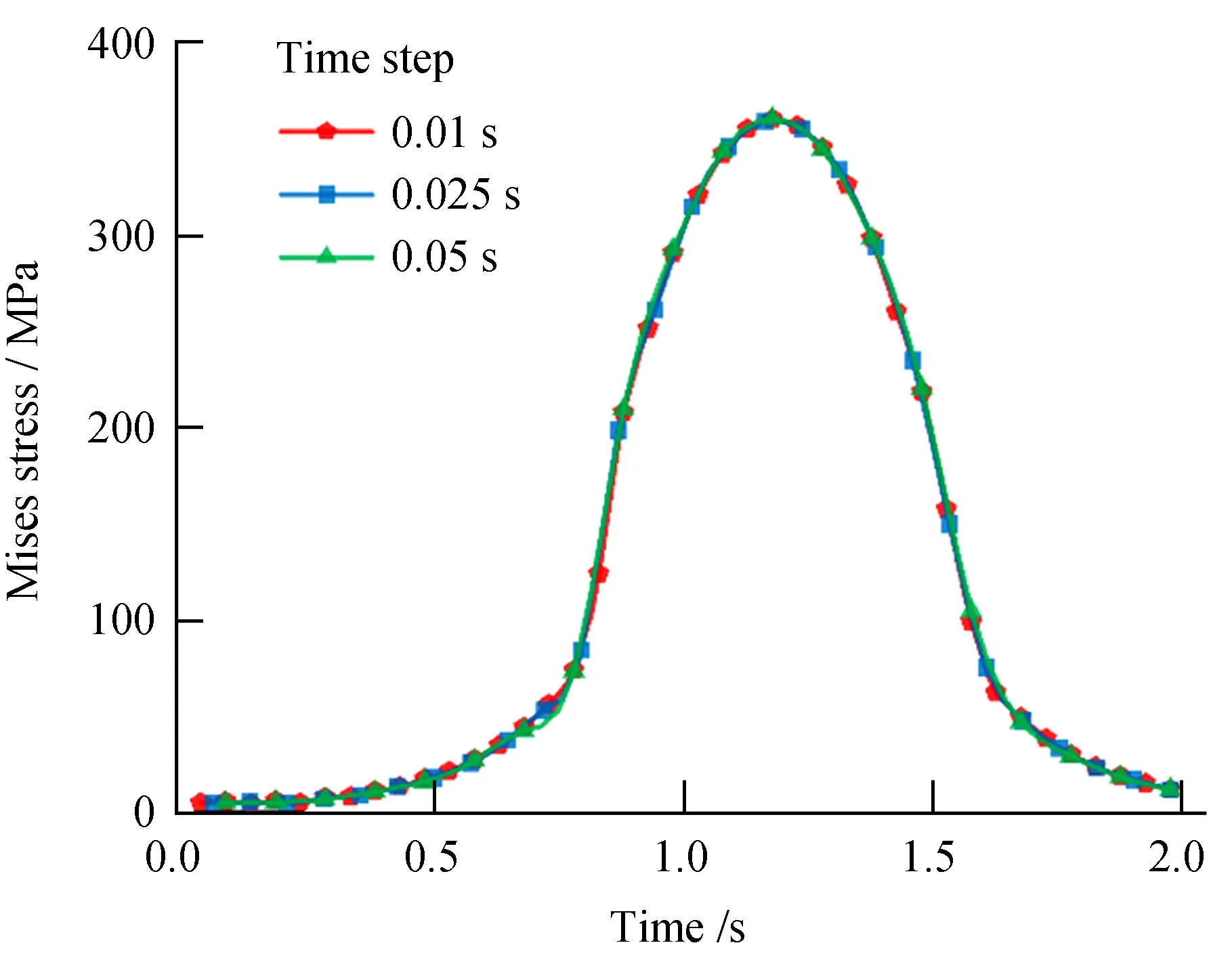
图2 时间步长对结果的影响Fig.2 The effect of time step on the results

基于赫兹接触理论，考虑天线滚轮位于焊缝处的静态工况，本文设置静摩擦系数为0.5。通过有限元数值分析，静态轮轨接触总变形量为0.147 mm，轨道最大变形量为0.069 mm，轨道受力云图如图3。

图3 (a)米塞斯应力云图；(b)接触压力云图；(c)最大剪应力云图Fig.3 (a) The pattern for Mises stress; (b) the pattern for contact pressure; (c) the pattern for maximum shear stress

由图3(a)可知，天线滚轮与轨道间的米塞斯应力最大值为363 MPa，与理论值371 MPa误差仅为2.2%，最大米塞斯应力出现在轨道表面下约4 mm处。由图3(b)可以看出，轮轨接触斑呈椭圆形，接触斑宽度为13 mm(理论值13.2 mm)，与赫兹接触理论基本吻合，最大接触压力为486 MPa(理论值489 MPa)，远小于轮轨材料42CrMo的屈服应力930 MPa，验证了天线静态工况下的安全性。由图3(c)可以看出，最大剪应力为117 MPa(理论值115 MPa)，但远小于轮轨材料的最大剪应力，且剪应力场出现在轨道表面下，可以反映真实轮轨接触应力场。静力学分析验证了模型的准确性，可用于瞬态分析。

3.2 瞬态分析

由于整个轮轨模型网格数量较大，瞬态分析计算量庞大，对计算机性能要求极高。基于模型中轮轨接触特点，采用减缩z向模型比例以减小模型计算量来进行瞬态分析。我们分别选取z向0.5，0.2和0.1的比例模型，其静力学计算结果与完整模型进行对比，结果如图4。从图4可以看出，随着z向模型比例的减小，减缩模型结果与原比例模型结果间的误差逐渐增大，为了兼顾计算精度与计算量，最终选取z向厚度为原模型的0.2进行瞬态分析。

3.2.1 摩擦系数影响分析

不同摩擦系数会引起滚轮与轨道间作用力的变化。摩擦系数分别取0.3，0.4和0.5与不考虑焊缝处材料影响的分析结果进行对比，轮轨间作用力的时变曲线如图5。轮轨间米塞斯应力出现两个快速变化的峰值，原因是焊缝过渡层与轨道存在变形差，滚轮接触到过渡层时，在轨道上出现应力集中，因此过渡层承受载荷快速减小。由于过渡层只有4 mm，滚轮迅速转过并抵达高硬度焊接区，应力集中又出现在表面焊接层。滚轮从轨道段进入焊缝过程中过渡层承受载荷最小，可以保障焊缝承载区域的焊接成功率。整个仿真过程中米塞斯应力最大变化量约22 MPa，该应力的突变在轨道长期服役过程中容易造成焊缝区域疲劳。

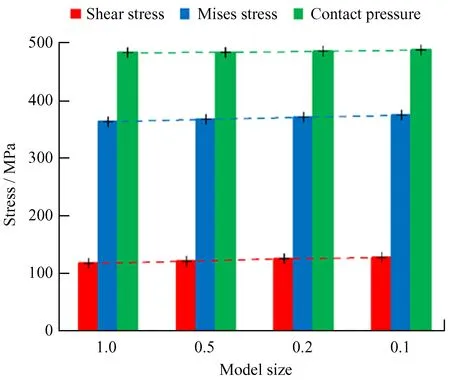
图4 z向不同比例模型计算结果

图5 不同摩擦系数的影响。(a)米塞斯应力时变曲线；(b)摩擦应力时变曲线

不同摩擦系数对轮轨间作用力影响较小，如摩擦系数为0.3与0.5之间的米塞斯应力差约为2.5 MPa，因此摩擦系数对轮轨间作用力的影响几乎可以忽略不计。摩擦系数主要影响轮轨之间的摩擦力。从图5(b)可以看出，随着摩擦系数的增大，轮轨间静、动摩擦应力都随之增大，且材料越软摩擦应力越大。考虑焊缝影响，滚轮在经过焊缝时，最大摩擦应力增加了71%，也增加了焊缝位置长期服役出现疲劳磨损的可能性。大型轮轨式天线由于滚轮负载大、速度低，一般不会出现滑动摩擦和滚轮打滑现象，因此,天线的日常维护可以通过涂抹润滑油来降低轮轨间的摩擦系数，从而降低摩擦应力。

3.2.2 轨道表面不平度的影响

110 m口径全向可动射电望远镜建成后，整个轨道表面不平度峰峰值优于0.3 mm，而轨道在制造及现场焊接装配过程中，不可避免地造成轨道表面不平。由于不平度的随机性和复杂性，本文使用文[15]的方法，用正弦曲线简化焊缝处表面不平度。以焊缝中心位置为原点，焊缝宽度为60 mm，依照图6(a)的正弦曲线改变焊缝位置处的节点坐标，实现有限元模型的修改。

在不同的表面不平度下，轮轨间作用力的时变曲线如图6(b)。从图6可以看出，滚轮在进入焊缝时，米塞斯应力出现快速减小又增大的现象，是因为通过坐标改变轨道表面不平度时，曲面与平面过渡处相邻两个节点出现了高度差。表面不平度为0.1 mm时，高度差约为0.005 mm，但造成应力的剧烈变化，侧面反映了重载天线轮轨接触时，局部微小缺陷(表面夹杂、气泡等)更容易对天线滚轮及轨道表面造成严重影响。随着轨道表面不平度的增加，米塞斯应力也随之增大。当轨道表面不平度为0.3 mm时，最大米塞斯应力为442 MPa，相比平顺轨道应力增加了约20%。焊缝表面不平度对天线的影响较大，天线运行时，需要时常对天线轨道进行检测和维护，保证天线轨道表面清洁，及时处理磨耗或装配带来的轨道表面不平度，减小对天线轮轨的损伤。

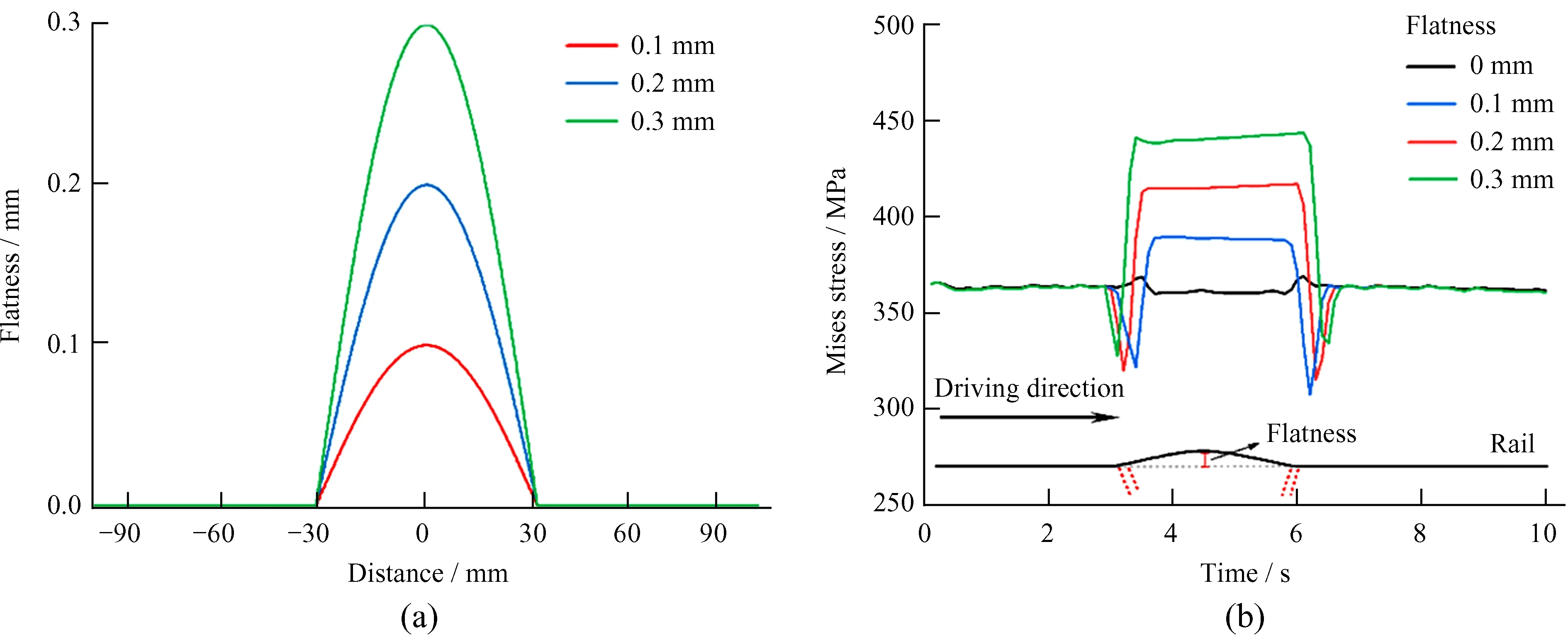
图6 (a)轨道焊缝不平度；(b)不同轨道表面不平度下的应力时变曲线Fig.6 (a) The rail welded joint flatness; (b) time-varying stress curves in different track surface flatness

分析可知，摩擦系数对轮轨间作用力影响较小，而焊缝处材料差异和轨道表面不平度更容易引起天线轮轨间作用力变化，应力的突变伴随着应力集中，对天线轨道的高周疲劳有着不良影响。

4 结 论

本文通过建立110 m口径全向可动射电望远镜轮轨模型，考虑轨道焊缝位置对轮轨瞬态接触的影响，研究了接触参数和轨道面形貌对轮轨间作用力的影响，主要分析结果为(1)采用层级细分技术对模型进行前处理，可以大大减小网格数量和计算成本，且模型具有较高的求解精度；(2)考虑焊缝材料差异时，静态工况下轮轨接触总变形量为0.147 mm，与瞬态相比接触变形量相差较小，但滚轮经过焊缝时轮轨间米塞斯应力发生剧烈变化，给轮轨长期有效服役带来不利影响；(3)不同摩擦系数对轮轨间作用力影响较小，主要影响轮轨间摩擦应力，且在滚轮经过焊缝时摩擦应力增大约71%。对大载荷天线轮轨间作用力影响较大的是轮轨接触面形貌的改变，由于轮轨间作用力大载荷、小集中的特点，轨道表面微小不平度会带来应力较大的变化，应保证天线轨道表面清洁，时常检测并及时处理。