石墨烯生产关键设备CFD-DEM模拟

2022-03-18周帅帅乔聪震卢春喜张经纬1c

中国粉体技术 2022年2期

周帅帅，李静，杨浩，乔聪震，卢春喜，张经纬,1c

(1.河南大学 a.纳米杂化材料应用技术国家地方联合工程研究中心;b.化学化工学院；c.纳米功能材料及其应用河南省协同创新中心； d.河南省催化反应工程中心，河南开封 475000；2.中国石油大学(北京) 化学工程与环境学院,北京昌平 102249)

石墨烯是一种以sp2杂化连接的碳原子紧密堆积成单层二维蜂窝状晶格结构的新材料[1]，具有优异的光学、电学、力学特性，在材料学、微纳加工、能源、生物医学和药物传递等方面具有重要的应用前景，被认为是一种未来革命性的材料。石墨烯的生产方法主要有机械剥离法[2-4]、氧化还原法[5]、取向附生法[6]、碳化硅外延法[7]、赫默法(Hummer)[8]和化学气相沉积法[9]等。其中机械剥离法制得的石墨烯通常保持着完整的晶体结构。液相剥离法作为机械剥离方法之一，具有工艺路线简单、易放大，剥离产物能较好地保持二维材料的性质等优点，是一种极具前景的规模化生产技术[10]。目前液相剥离法主要存在生产效率低、成本高、片层易碎化等问题[11-13]。通过对液相剥离液固体系多相流动特性的定量描述，可为提高液相剥离的生产效率提供指导。液相剥离过程一般在搅拌釜内进行[13]，搅拌釜内液固两相流场较为复杂。以往针对搅拌釜内液固体系的研究主要集中于颗粒悬浮临界转速、悬浮机理、两相流动特性等[14-15]，关于单颗粒在流场中运动特性的报道较少。已有关于单颗粒在流场中运动特性相关报道主要采用实验法和模型法。其中实验手段主要包括粒子图像测速(particle image velocimetry，PIV)技术、热线风速仪、激光多普勒测速(laser doppler velocimetry，LDA)技术和激光超声测量技术；模拟手段主要包括格子-玻尔兹曼方法(Lattice Boltzmann method，LBM)和计算流体动力学-离散元法建模(computational fluid dynamics-discrete element modeling，CFD-DEM)方法[14-17]。Mo等[14]和莫君媛[15]采用高速摄像技术考察了圆盘桨驱动的方形搅拌槽内层流工况下单个颗粒的临界悬浮运动，并利用LBM对单颗粒存在时的两相流场进行了直接数值模拟，结果表明，颗粒的悬浮动力与截面积无关，而与体积成正比，颗粒所受的压力梯度力是悬浮的主要动力。候家鑫[16]通过CFD-DEM耦合的方法研究了椭球形颗粒长径比等参数对颗粒的运动和传热特性的影响，结果表明，长径比为1.5时颗粒在管内运动最剧烈，颗粒取向夹角概率曲线峰值最大，对应颗粒-流体间相互作用面积最大，相互作用力最大。Shao等[17]利用CFD-DEM法对搅拌槽内球形颗粒的运动进行模拟，结果表明，颗粒具有剧烈的自旋运动，导致颗粒受到额外的剪切力，而此剪切力可能会对颗粒产生破碎作用。针对石墨烯液相剥离过程中液固体系颗粒运动未见相关报道，本文中拟采用CFD-DEM法对搅拌釜内液固体系进行模拟分析。

1 建模

针对石墨烯液相剥离过程所涉及的液固多相流场，采用CFD-DEM法对其进行研究。通过CFD计算软件获得流场信息，基于该流场信息，利用DEM法计算出颗粒的运动状态，通过2种方法信息的共享实现流固耦合计算。

1.1 液相控制方程

采用CFD-DEM方法对石墨烯搅拌釜内液固体系进行模拟计算，利用Fluent软件中的欧拉模型对液相进行计算，利用多用途离散元法建模(multipurpose discrete element modeling，EDEM)方法对颗粒的运动进行计算。液相控制方程主要包括连续性方程、动量守恒方程和湍流模型方程。基于液相不可压缩假设，对应的控制方程可以写成如下形式。

连续性方程为

(1)

式中：αl为液相的体积分数，%；ρl为流体密度，kg/m3；u为流体速度，m/s；t为时间，s。

动量守恒方程为

(2)

式中：S是液相与颗粒相之间相互作用的合力，N·m-3；p为静压强，Pa；g为重力加速度，m/s2;μl为流体黏度，Pa·s。

选择可实现的k-ε湍流模型[18]来计算液相的湍流运动，控制方程为

(3)

(4)

(5)

式中：k和ε为模型参数，均为常数；μt为湍动黏度；Pa·s；δk为k的湍动普朗特数，取值1.0；Gk为由平均速度梯度产生湍流动能，J；δε为ε的湍动普朗特数，取值1.2；C1、C2、Cμ均为模型参数，C1=1.44，C2=1.92，Cμ=0.99。

1.2 颗粒运动的离散元模型

颗粒的传输运动主要取决于其所受合力，而旋转运动主要受接触力矩控制。

(6)

(7)

式中：mi为颗粒i的质量，kg；vi为颗粒i速度，m/s；Fn,ij与Ft,ij分别是颗粒i和颗粒j之间的法向和切向接触力，N；Fd,i、FM,i和Fb,i分别是颗粒i所受的曳力、马格努斯力和浮力，N；Ii是颗粒i的动量，kg·m2；Tt,ij和Tr,ij分别是颗粒i与颗粒j之间由切向力和径向力所产生的力矩，N·m；ωi为颗粒i的角速度，rad/s；

除了液固接触力，曳力Fd和马格努斯力FM还存在颗粒-颗粒、颗粒-器壁、颗粒-搅拌桨之间碰撞力。

1.2.1 颗粒-颗粒碰撞力

2个球形颗粒之间的接触力和接触力矩主要基于Hertz-Mindlin模型[19-20]。颗粒之间的法向力Fn,ij为

(8)

(9)

(10)

颗粒之间的切向力Ft,ij为

(11)

(12)

(13)

力矩计算公式为

Tt,ij=LijnijFt,ij,

(14)

(15)

式中：Tt,ij为力矩的切向分量；N·m;Tr,ij为力矩的径向分量，N·m；Lij为颗粒i的中心到与颗粒j接触平面的距离，m；nij代表2个接触颗粒的法向单位向量；ωij为接触点角速度向量，rad/s；μr为滚动摩擦系数。

1.2.2 颗粒与器壁和颗粒与搅拌桨之间的碰撞

在颗粒和器壁的碰撞过程中，其所涉及的力和力矩与颗粒间的类似，如式(8)—(15)所示。针对低浓度体系，颗粒对器壁和颗粒对搅拌桨的作用在计算中可以忽略。

与颗粒与器壁之间的碰撞不同，搅拌桨的转动导致颗粒与搅拌桨之间的碰撞更为复杂。搅拌桨沿着切向运动会影响颗粒的切向运动。在每个时间段的碰撞过程中，所涉及的力和力矩均可以基于式(8)—(15)进行计算。DEM模拟的计算步长为1.5×10-6s，搅拌桨对应的位移为3.14×10-6m，搅拌釜内颗粒粒径级别为10-3m，设置合适的Releigh步长。

动量源相S是液固相间一个基于体积计算的合力。在计算过程中，液固两相间的作用力主要考虑了浮力Fb、曳力Fd和马格努斯力FM，因此对应的S为

(16)

式中：Fp为CFD单个计算网格内流体所受合力，N；Vcell为CFD单个计算网格体积，m3。

1.2.3 曳力

采用Di Felice曳力模型[21]计算曳力，即

Fd=Fd0α-(β-1),

(17)

(18)

β=3.7-0.65exp[-(1.5-lgRep)2/2],

(19)

(20)

(21)

式中：Fd0为单个曳力，N；αp为颗粒体积分数，%；β为模型参数；Cd为曳力系数；dp为颗粒粒径，m；Rep为颗粒雷诺数。

1.2.4 马格努斯力

当一个旋转的物体进入流体内部，由于流体的涡旋，就会在垂直流线方向产生马格努斯力。马格努斯力计算公式[22-23]为

(22)

(23)

(24)

(25)

式中：ωl是液相局部速度，rad/s；ωp是颗粒的角速度，rad/s；CL为模型参数；Rel为液相雷诺数。

1.3 CFD-EDEM耦合工作原理

CFD和EDEM联用(耦合)可以同时实现液相流场计算和颗粒运动计算，图1所示为CFD-EDEM耦合工作机理。在耦合模拟中，Fluent软件首先对流体进行计算，通过雷诺平均N-S方程计算后，相关流场信息传递给EDEM。EDEM中的DEM模块计算在相应流场条件下颗粒的受力及运动轨迹，计算结果反馈给Fluent软件。这个过程循环进行直到迭代结果收敛。在计算过程中，由于颗粒较少，对应的体积分数较低，因此可忽略颗粒的体积分数。

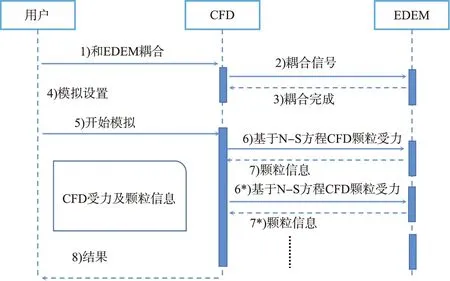
图1 CFD-EDEM耦合工作原理Fig.1 Coupling mechanism between CFD and EDEM

1.4 实验装置模型及网格划分

对一个实验室规模的搅拌釜反应器进行模拟计算。该搅拌釜反应器由玻璃制成，其搅拌桨为直叶式搅拌桨。实验装置基本参数见表1。

表1 实验装置的基本参数Tab..1 Parameters of experimental unit

根据以上参数，采用ANSYS软件中Design Molder模块对实验装置进行绘制，并采用Meshing模块对实验装置进行网格划分，网格划分采用四面体网格，最大边长控制为2 mm，共有616 813个网格，结果如图2所示。

图2 实验装置模型及网格划分Fig.2 Experimental apparatus model and corresponding mesh

1.5 模型设置

1.5.1 Fluent软件设置

CFD在搅拌釜式反应器模拟中的应用可以追溯到20世纪70年代，近年来CFD技术的发展都可以从该反应器的应用中体现出来。搅拌釜内部的流场是十分复杂的，流动变量的变化，特别是湍流参数的变化有时会达到2～3个数量级[24]，这对搅拌釜反应器的影响十分重要。从数值模拟的角度来看，模拟搅拌槽的一大难题是如何处理好运动的桨叶与静止的挡板、槽壁之间的相互作用。为了解决这个问题，已经提出了不同的模拟方法：黑箱模型法、内外迭代法、多重参考系(MRF)法和滑移网格(SG)法等[25]。本文中选用MRF法进行模拟，桨叶及其附近流体区采用旋转坐标系，其他区域采用静止坐标系。相对于滑移网格，MRF法较为简单。整体的计算域被分为2类：一部分区域和旋转区域相关联，一部分区域和静止的壁面关联。内部旋转的区域的控制方程在旋转参考系下求解(其中添加了科氏力以及离心力)，外部区域则在静止参考系下求解。静止区域和旋转区域之间通过一个界面匹配，在这个界面中，速度将进行相应的调整以匹配不同的参考系控制方程。在速度的转化中，假定界面处是稳态的流动。其中Fluent软件参数设置见表2。

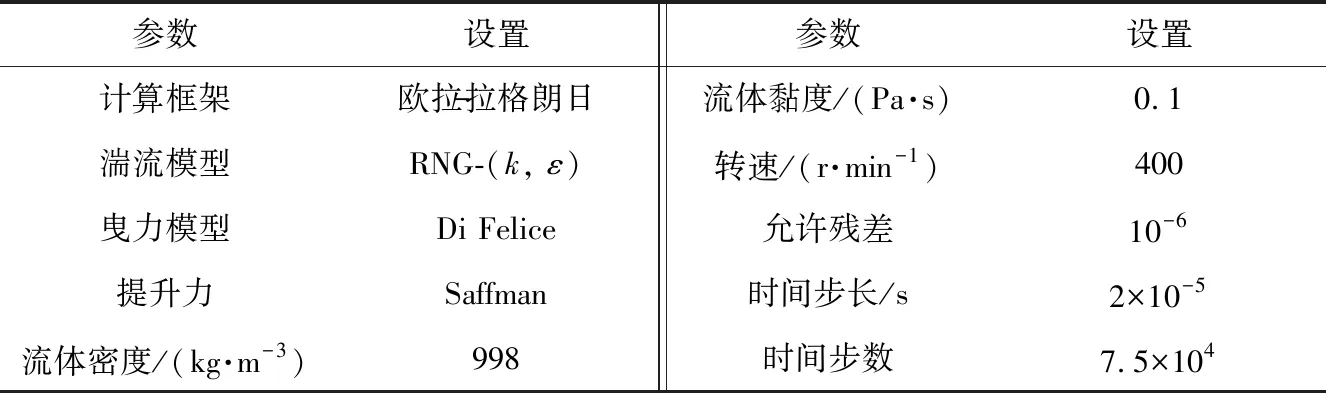
表2 Fluent软件参数设置Tab..2 Parameters adopted in fluent software

1.5.2 颗粒信息

为了获取颗粒信息，采用扫描电子显微镜(SEM,德国蔡司公司)对石墨烯生产原料-鳞片石墨的形貌进行观察，图3为石墨颗粒的SEM图像。由图可以看出，石墨颗粒表面较为粗糙，且球形度较低。

图3 石墨颗粒的SEM图像Fig.3 SEM images of graphite particles

结合本研究中以获取石墨颗粒在流场中的夹角为主要出发点，采用片状颗粒模拟石墨颗粒在搅拌釜中的运动特性，从而强化剥离效率，并采用多个球形颗粒串并联的形式模拟石墨颗粒，模型颗粒结构如图4所示。

图4 模型颗粒结构Fig.4 Structure of model particles

模型颗粒的三维尺寸长度、宽度、高度分别为2.1、1.6、0.05 mm。颗粒相主体材料参数及设备主体材料参数如表3所示。

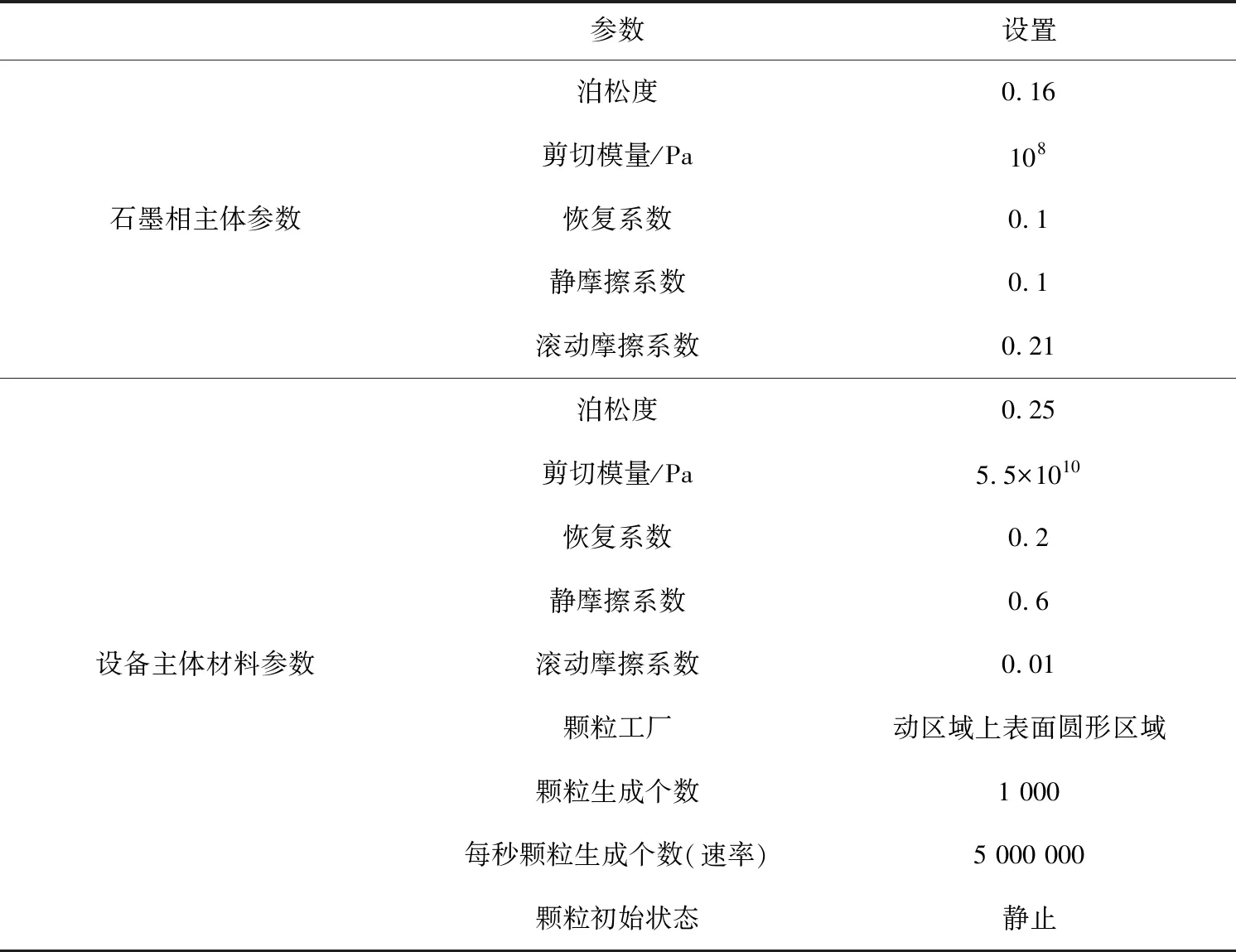
表3 EDEM参数设置Tab..3 Parameters adopted in EDEM

2 模型验证

为了验证模型的准确性，通过气液两相实验对所建模型进行验证。实验过程中发现，气液两相在搅拌釜内存在如图5所示的分界面。由图可以看出，该分界面接近抛物线分布，呈现出边壁高、中心低的特点。引入液面边壁高度hw和液面中心高度hc这2个参数用于该分界面的定量描述。采用上述模型，基于流体容积模型(VOF)两相流，分界面高度计算结果与实验结果对比见表4。

图5 搅拌釜反应器气液界面Fig.5 Interface between gas and liquid in stirred tank reactor

模型计算结果与实验结果进行了对比，图6所示为转速为400 r/min时对应的结果对比。结合图6与表4可以看出,计算结果与实验结果较为吻合，因此可以确定模型的适用性。

表4 分界面高度计算结果与实验结果对比Tab..4 Comparison between computational and experimental height of interface

(a)计算结果(b)实验结果图6 转速为400 r/min时不同分界面高度结果对比Fig.6 Comparison between different results of interface height with speed of 400 r/min

3 模拟结果

由于分别采用Fluent软件和EDEM软件对液相和颗粒相的运动进行分析，因此计算结果的分析也分为液相和颗粒相2个方面进行阐述。

3.1 液相运动特性

液相流动信息是反映液-固体系相互作用规律的关键信息，通过考察液相速度、剪切力的轴径向分布特性，可以间接获取两相相互作用规律。将液相结果分为2个部分进行讨论，分别为液相速度分布和液相剪切力分布。

3.1.1 液相速度的轴、径向分布

液固两相的耦合采用欧拉-拉格朗日方法，液相的计算框架基于欧拉模型，颗粒相的计算框架基于拉格朗日模型，因此并未考虑颗粒相的体积分数。图7是液相速度沿轴向和径向截面的分布云图。由图7(a)可以看出，在搅拌桨附近，液相具有较大的速度，介于7～8 m/s之间；而靠近搅拌轴区域，液相速度几乎为0。随着径向位置远离搅拌轴，液相速度逐渐增大，而当径向位置靠近边壁时，液相速度再次减小。这与研究采用的边壁无滑移边界条件有关。无滑移边壁条件认为液相在边壁处速度为0。由图7(b)可以看出，液相速度在搅拌桨附近具有较大的数值。在4个搅拌桨之间的区域内，液相速度减小，且随着距离搅拌轴的径向位置减小而减小。对比不同截面液相速度的分布特性，可以看出,搅拌桨对搅拌釜内液相速度分布的影响主要集中在靠近搅拌桨的轴向区域内(z=25～35 mm，z为轴向高度)，而在远离搅拌桨区域内(z=35～75 mm)，液相速度沿着径向截面的分布具有较好的规律性，即液相速度在远离边壁和远离搅拌轴、径向区域内均具有较大的数值，且沿着周向变化较小。

3.1.2 液相剪切力的轴、径向分布

在石墨剥离过程中，其剥离效率主要取决于剪切作用力。根据黏性剪切定律，液固两相体系内剪切力τ的计算公式为

(22)

式中：du/dr为液相沿径向的速度梯度，s。

(a)轴向截面(b)径向截面图7 搅拌釜内液相速度沿轴向、径向截面的分布云图Fig.7 Distribution cloud diagram of liquid phase velocity along axial and radial cross section in stirred tank

本文中采用的流体为非牛顿流体，其黏度随着运动状态会发生变化，无法考察单一变量，如：黏度和速度梯度(剪切速率)，对剪切力的影响。黏性剪切应力主要取决于速度梯度及流体物性，其计算公式为

(26)

式中：u为液相沿着x方向的速度，m/s；v为液相沿着y方向的速度，m/s。

直接通过CFD-Post软件计算出剪切力的分布，并通过将计算出的剪切力以图形的形式进行保存，即可获得剪切力分布云图。据此获得的剪切力分布云图如图8所示。

图8为剪切力沿不同截面的分布云图。由图8(a)可以看出，剪切力主要分布在搅拌桨周围、边壁周围和搅拌桨以上环流区域。这主要是由于这3个区域内均具有较大的速度梯度，因此具有较高的剪切速率。除此之外的区域内，液相剪切力较小，基本接近0，因此，为了实现石墨剥离过程较高的剥离效率，应通过调整操作条件使得石墨颗粒尽量分布在这些具有较大剪切力的区域内。由图8(b)可以看出，剪切力沿着径向截面的分布与液相速度类似。剪切力主要集中于桨叶边缘和搅拌釜器壁附近区域。在以搅拌桨边缘为直径的环形区域内，剪切力明显增大。

(a)轴向截面(b)径向截面图8 剪切力沿轴向、径向截面的分布云图Fig.8 Distribution cloud diagram of shear force along axial and radial cross sections

图9是不同轴向高度时剪切力沿径向截面的分布云图。从图中可以看出，随着轴向高度的增加，剪切力沿着径向截面分布均匀性逐渐提高，而剪切力的数值逐渐减小。当轴向位置由z=25 mm增大到45 mm时，剪切力较大的区域逐渐消失，对应剪切力较小的区域开始处于主导地位。当轴向位置由z=45 mm增大到75 mm时，剪切力沿径向截面的分布变得越来越均匀，而剪切力较小的区域开始处于主导地位。这说明，在靠近桨叶的区域内，剪切力较大，而在远离桨叶区域内剪切力较小，因此，为了保证较高的石墨剥离效率，应使尽可能多的颗粒处于靠近桨叶的区域。

图9 不同轴向高度z时剪切力沿径向截面的分布云图Fig.9 Distribution cloud diagram of shear force along radial cross sections with different axial height z

3.2 颗粒相运动特性

颗粒相运动特性结果分析主要包括颗粒相分布、颗粒运动轨迹以及颗粒受力分析。颗粒相分布特性如图10所示。由图可以看出，部分颗粒堆积于搅拌釜边壁区域，这主要是由于石墨颗粒具有不规则的形状，且表面较为粗糙，因此在近边壁区域具有较大的阻力，从而导致部分颗粒集聚。分散颗粒也主要集中分布在搅拌釜边壁附近，这主要与颗粒所受力有关。由于壁面和石墨颗粒之间静摩擦阻力较大，导致石墨颗粒在静摩擦阻力的作用下堆积于搅拌釜器壁周围。在搅拌釜近壁面区域内，流体运动趋于层流，这使得径向的动量传递得到抑制，进而使得边壁附近的颗粒沿着径向的运动受到阻碍，从而堆积于近壁面区域。在搅拌时间为0.10～1.5 s的过程中，颗粒在近壁面区域的堆积逐渐增加，近壁面区域颗粒个数也随之增大，这并不利于石墨剥离过程的进行，因此，如何调节实验条件，进而降低堆积现象是提高石墨剥离效率的关键。

图10 颗粒分布特性Fig.10 Variation of particle phase distribution behavior

图11所示为颗粒相分布随搅拌时间变化规律。由图可知，随着搅拌能量的输入，颗粒体系逐渐沿着轴向分散开，并同时具有轴向、周向和径向3个方向的动量，其中周向运动占主导。随着搅拌进行，轴向和径向的速率逐渐变为0，周向速率稳定在某一数值，因此，剪切作用力是片状颗粒运动主要作用力。

图11 颗粒相分布随搅拌时间变化规律Fig.11 Variation of particle distribution with time flow along axial cross-section

图12是单个颗粒的运动轨迹示意图。单个颗粒整体运动可以分为3个方向：径向、周向和轴向。颗粒在流体作用下沿着周向作周期运动。颗粒沿着径向的起始运动主要与颗粒的起始位置有关，其周期性特性受边壁颗粒堆积的影响，表现并不明显。颗粒沿着轴向也呈现出周期性规律，这主要与液相的流动特性有关。如前所述，液相沿着轴向形成一个较大的漩涡，液体在漩涡内作周期运动，因此导致颗粒跟随着液相作周期运动。

图12 单个颗粒的运动轨迹示意图Fig.12 Schematci diagram of single particle trajectory

模拟结果表明，颗粒合力在大多数时间内为0，而在0.081、0.976、1.14、1.30 s处附近会出现较大的波动。主要原因是颗粒与搅拌桨或搅拌槽壁碰撞所产生的作用力。该力具有作用时间短且数值大的特点。

由实验及模拟结果可以发现，机械力是改变颗粒运动特性的重要因素；搅拌釜内剪切应力主要集中于搅拌桨附近及搅拌釜器壁附近区域，占整个搅拌釜空间较小，因此，在进行搅拌反应器优化时应在搅拌釜器壁或搅拌釜内加入内构件，增大机械力作用范围；另外，也可通过调整搅拌桨的运行方式，如加入周期性的正-反转，使得颗粒与液相具有更大的相对速度，从而提高剪切应力的绝对值。以上优化方案均提高石墨剥离效率作为出发点。