基于变分模态分解的侵彻过载信号盲分离
2022-03-18张晨阳李世中
张晨阳, 张 亚, 李世中
(中北大学 机电工程学院, 太原 030051)
引信仿真测试是评价引信综合性能的有效途径,对于提升硬目标侵彻武器的攻击能力具有重要意义。开展引信仿真测试系统的研究,能够缩短引信的研制时间、节省研制费用、提高研制质量,为引信的总体设计和建立完善的引信评价体系提供技术保障[1]。在侵彻过程中,弹体与弹靶的作用过程十分复杂,有多种振动信号作用在弹体上,获得的侵彻过载信号不仅包含弹体自身的刚体加速度信号,还叠加了各种噪声信号。因此,将弹体的刚体加速度信号从侵彻过载信号中分离出来,是引信仿真测试的关键一步。
对于侵彻过载信号的处理,已经展开了多方面的研究。张兵等[2]在压电传感器的两端加入三种减震片,通过弹体冲击试验发现,加入减震片后传感器输出信号的频率范围有了明显缩小,并且三种不同材质的减震片分别可以滤除大于4 kHz、7 kHz、10 kHz的噪声信号。黄娟等[3]提出一种小波去噪与HHT变换相结合的故障信号提取方法,先对时域信号进行小波去噪,再采用HHT变换进行时频分析,根据分析得到一系列本征模态函数判断轴承的故障情况。赵海峰等[4]提出一种基于奇异值分解的侵彻过载信号降噪方法,通过对侵彻过载信号进行奇异值分解,由主体奇异值分量稳定原则确定信号重构矩阵,从而去除侵彻过载信号中的噪声分量,提取出弹体的刚体加速度信号。毋文峰等[5]采用经验模态分解对单通道信号进行盲分离,提取含有不同故障信息的本征模态函数与原单通道信号组成多维信号,利用奇异值分解重构多通道混合信号,对多通道混合信号进行盲源分离,但由于经验模态分解在分解过程中存在欠包络、过包络、模态混叠、端点效应等问题,使得信号处理结果差强人意。集合经验模态分解[6]虽然在一定程度上解决了模态混叠问题,但同时加大了算法的计算量,且端点效应问题仍未解决。
本文提出一种基于变分模态分解的侵彻过载信号盲源分离算法。为了将单通道信号转化为多维信号,首先对信号进行变分模态分解,由本征模态函数和单通道信号组成多维信号;然后对多维信号的自相关矩阵进行奇异值分解估计源信号数目,并计算各本征模态函数与单通道信号的相关系数,由相关系数的大小选择相应的本征模态函数与单通道信号重构多通道信号;最后利用盲源分离中特征矩阵联合近似对角化算法(joint approximate diagonalization of eigenmatrices, JADE)[7]对多通道信号进行盲源分离。
1 理论基础
1.1 盲源分离算法
盲源分离是一种在信号传输路径的各项参数与信号源均未知的情况下,根据输入源信号的统计特性,由混合观测信号还原出源信号独立成分的信号分离算法。根据源信号数目小于、等于和大于观测信号数目,可将盲源分离分为超定、正定和欠定盲源分离三种[8]。传统的盲源分离算法主要针对源信号信息充足的超定和正定盲源分离,而对于欠定盲源分离,由于其观测信息缺乏,现有的盲源分离算法不能有效地求解出源信号的估计信号[9]。
假设源信号S(t)由N个未知的独立信号组成,经未知的信道传送后,由M个传感器采集获得观测信号X(t),盲源分离的数学模型见式(1)
X(t)=AS(t)
(1)
式中:X(t)=[X1(t),X2(t),…,XM(t)]T为M维观测信号;S(t)=[S1(t),S2(t),…,SN(t)]T为N维源信号;A为M×N阶混合矩阵。
盲源分离就是在S(t)和A都未知的情况下寻求一个N×M阶的矩阵W,通过该矩阵和观测信号X(t)分离出源信号S(t)的近似估计信号Y(t)[10],盲源分离过程如图1所示。
Y(t)=WX(t)
(2)
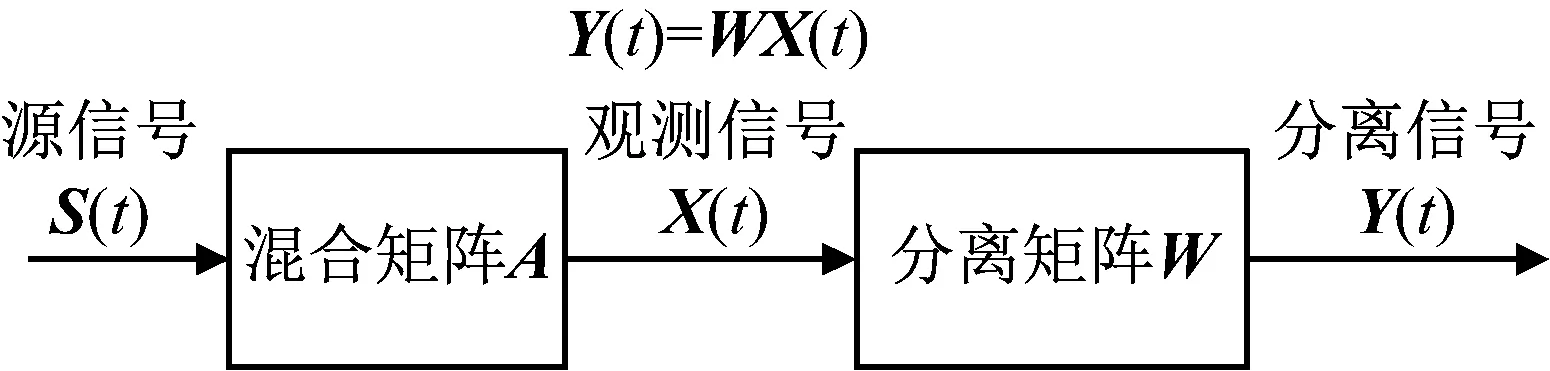
图1 盲源分离过程图
1.2 变分模态分解
变分模态分解(variational mode decomposition, VMD)是由Dragomiretskiy等[11]根据维纳滤波和变分思想提出的一种尺度可变的信号分解算法,通过将信号自适应地分解为若干个本征模态函数,采用交替方向乘子法迭代求解各模态的中心频率,从而将各模态解调至对应的基频带。与经验模态分解的递归式分解不同,VMD是在变分模型的约束下进行信号的分解过程,具有完备的理论支撑,在复杂信号分析领域里具有广泛应用[12]。
变分模态分解将源信号分解为有限个具有限带宽的本征模态函数,每个本征模态函数围绕在其中心频率附近,以各本征模态函数的带宽之和最小为约束条件,建立约束变分模型(见式(3)),寻求各个信号分量对应的本征模态函数,从而将源信号自适应地分解为各本征模态函数的线性组合。
(3)
式中:{uk}={u1,u2,…,uK}为K个本征模态函数;{ωk}={ω1,ω2,…,ωK}为K个本征模态函数对应的中心频率。
为了求解约束变分模型,引入二次惩罚因子α和拉格朗日惩罚算子λ(t),将变分模型最优解的约束变分问题转化为非约束变分问题,通过交替方向乘子法在傅里叶域内求解该非约束变分问题,表达式见式(4)
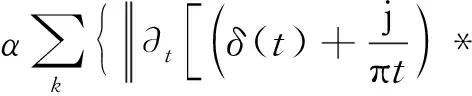
(4)
通过不断更新各本征模态分量的中心频率和带宽,并根据源信号的频域特性划分频带,从而将源信号自适应地分解为一系列本征模态函数,其中各变量的更新见式(5)~式(8),算法求解流程如图2所示。
(5)
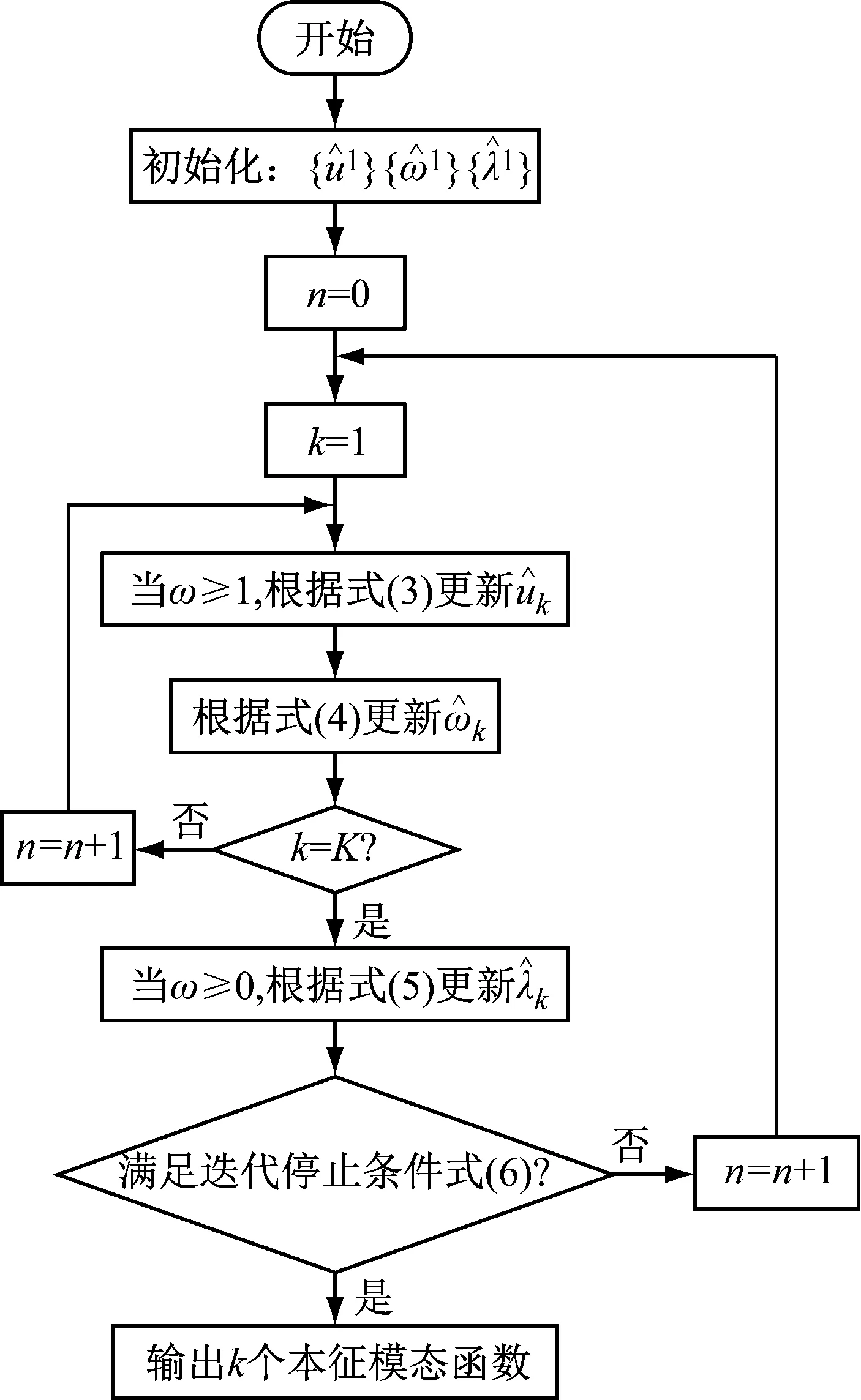
图2 VMD算法流程图
(6)
(7)
(8)
式中:n=n+1;k=1,2,…,K;τ为预设误差。
2 基于VMD的盲源分离算法
在盲源分离算法中,要求观测信号数目大于或等于源信号数目,而在实际情况中观测信号数目往往小于源信号数目,且有时只能采集到单通道观测信号,为了解决单通道观测信号盲源分离问题,提出一种基于VMD的盲源分离算法。首先由VMD将单通道观测信号自适应地分解为若干个本征模态函数,并将单通道观测信号与各本征模态函数组成多维信号;然后利用奇异值分解估计单通道观测信号的源信号数目[13],并计算各本征模态函数与单通道观测信号的相关系数,根据源信号数目,选择相关系数较大的本征模态函数与单通道观测信号重构多通道观测信号;最后采用盲源分离中的JADE算法对多通道观测信号进行盲源分离,算法流程如图3所示。
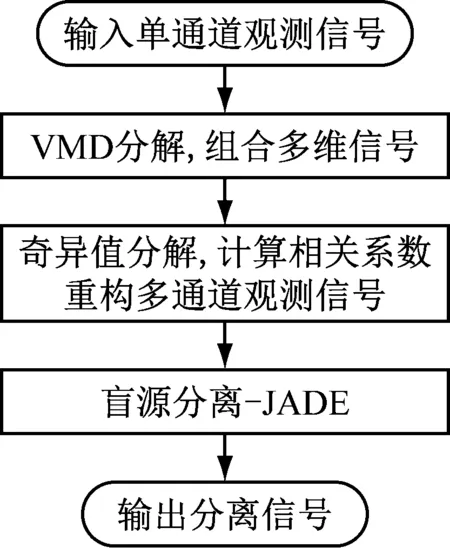
图3 基于VMD的盲源分离算法流程图
2.1 重构多通道观测信号
首先选择适宜的采样频率和本征模态函数个数K,通过对单通道观测信号X(t)进行变分模态分解,从而将X(t)自适应地分解为K个本征模态函数X(t)IMF=[IMF1,IMF2,…,IMFK];然后将X(t)与K个本征模态函数组成多维观测信号y(t)=[X(t),IMF1,…,IMFK],即解决了盲源分离中观测信号数目小于源信号数目的问题。对y(t)的自相关矩阵进行奇异值分解,y(t)的自相关矩阵Ryy见式(9),对Ryy进行奇异值分解见式(10)
Ryy=E[y(t)×yH(t)]
(9)
Ryy=UΛVT
(10)
式中:U为左奇异向量;V为右奇异向量;Λ=diag{λ1,λ2,…,λn}为奇异值向量对应的特征值;yH(t)为多维观测信号y(t)的共轭转置。
Λ中前几个特征值的数值较大,已经包含信号中的大部分信息,通过计算自相关矩阵Ryy的特征值的数值占比(见式(11)),即可估算出单通道观测信号的数目。
(11)
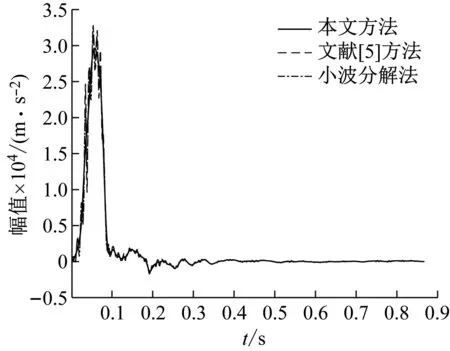
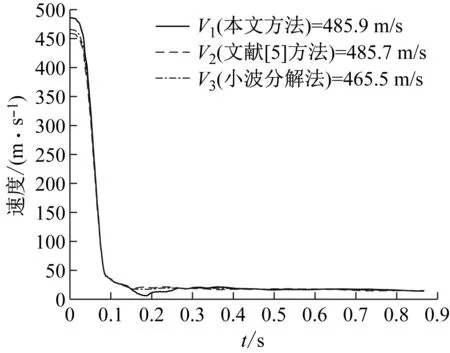
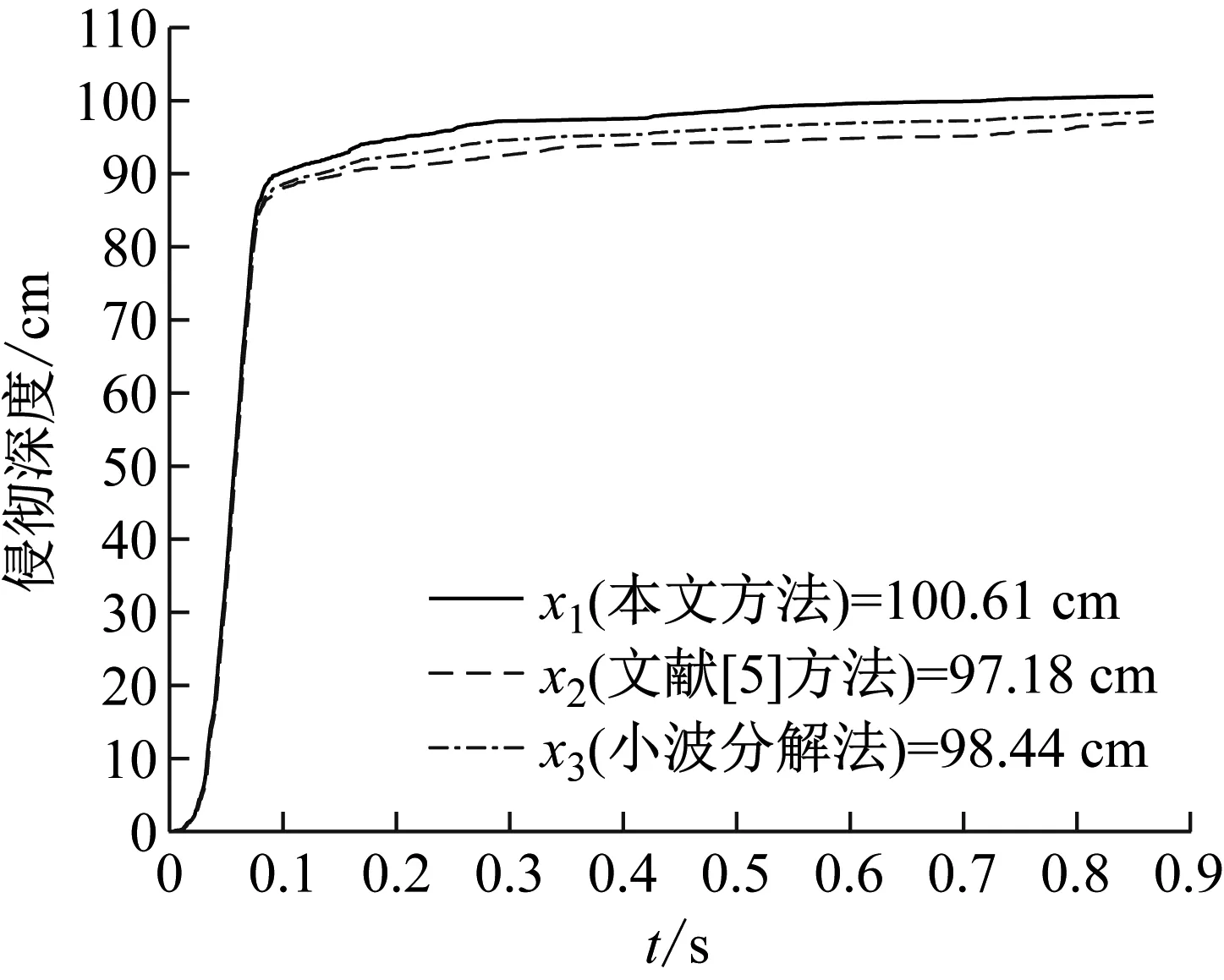
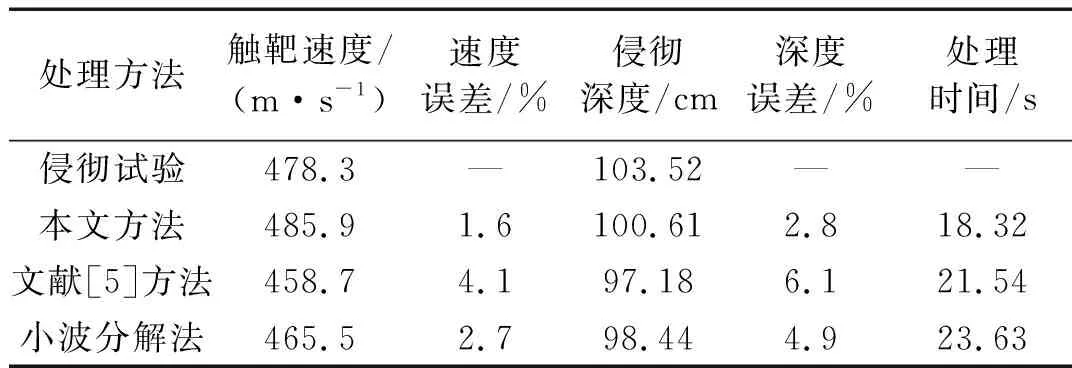
当m值取i(1≤i 确定源信号的数目后,通过计算各本征模态函数与X(t)IMF的相关系数(见式(12)),选择相关系数较大的前m-1个本征模态函数,与X(t)重构多通道观测信号H(t)=[X(t),IMF1,…,IMFm-1]。 ρ(X(t),IMFi)= (12) 采用盲源分离中的JADE算法对多通道观测信号H(t)进行分析处理。首先对H(t)进行去中心化和白化处理,求得白化矩阵W,由盲源分离模型可得白化信号Z(t)见式(13) Z(t)=WX(t)=WAS(t)=US(t) (13) 式中,U为一个N×N阶的酉矩阵。 从而将求解混合矩阵A转化为计算酉矩阵U。取一任意的N×N阶矩阵M,则白化信号Z(t)的四阶累积量矩阵的第a行第b列元素为见式(14) (14) 式中:QZ(M)为Z(t)的四阶累积量矩阵;Pabcd(Z)为Z(t)的第a,b,c,d分量的四阶累计量;mcd为矩阵M的第c行第d列元素。 将UTQZ(Mi)U中对角元素的平方和(见式(15))作为矩阵对角化的目标函数,通过最小化目标函数F(U)求解出酉矩阵U,即可求出源信号的估计信号Y(t)见式(16)。 (15) Y(t)=UTWX(t) (16) 采用弹载测试系统进行侵彻试验以获得侵彻过载信号时间历程曲线。试验过程如下:侵彻试验前在试验弹体底部安装弹载测试系统,在弹体侵彻过程中由弹载测试系统中的传感器模块采集弹体与弹靶产生的侵彻过载信号;侵彻过载信号经信号调理模块升压、整流、放大、滤波后,传送到数据采集存储模块中进行模数转换并存储到数据存储器中;侵彻试验结束后,通过弹载测试系统的数据接口读取试验数据。测试系统架构如图4所示,试验结束后,通过测试系统的数据接口将数据读取出来。试验测得的弹体侵彻过载信号曲线如图5所示,试验测得弹体侵彻深度为103.52 cm,弹体触靶速度为478.3 m/s。 图4 测试系统架构图 图5 侵彻过载信号时间历程曲线 以1 kHz的采样频率对试验获得的侵彻过载信号进行变分模态分解。通过对K取2~10,将各本征模态函数的中心频率按从低到高排列,观察其中心频率的变化情况,如表1所示。由表1可知,当K取8时,中心频率在454 Hz左右的本征模态函数信息丢失;K取10时,第8个分量的中心频率738 Hz和第9个分量的中心频率787 Hz较为接近,容易出现模态混叠现象。因此将本征模态函数的分解个数K设置为9,各本征模态函数图像如图6所示。 表1 不同模态个数时各模态的中心频率 (a) IMF1~IMF5函数图像 将9个本征模态函数与侵彻过载信号组成多维观测信号y(t),对y(t)的自相关矩阵Ryy进行奇异值分解,得到各奇异值向量对应的特征值,并计算各特征值及前n个特征值在全体特征值中所占比例,如表2所示。 表2 特征值占比及前n个特征值占比 由表2可知,当n=3时,前3个特征值在总体特征值中占比为98.59%;当n>3时各特征值占比均小于1%,表明前3个特征值已经包含多维观测信号y(t)中的大部分信息,因此源信号的估计数目为3。然后计算各本征模态函数与侵彻过载信号的相关系数,选择相关系数最大的2个本征模态函数与侵彻过载信号重构多通道观测信号,计算结果如表3所示。 表3 各本征模态函数与侵彻过载信号相关系数 由表3可知,η5与η7在9个相关系数中数值较大,因此选择IMF5、IMF7与侵彻过载加信号X(t)重构多通道观测信号H(t)=[X(t),IMF5,IMF7],采用JADE对多通道观测信号H(t)进行盲源分离,分离出的信号分量如图7所示。 (a) 分量1 由图7可知,H(t)经本文方法处理后分离出3个信号分量。其中,分量1的加速度幅值曲线较为光滑,由式(14)计算分量1与侵彻过载信号的相关系数ρ=0.952 7,可认为分量1包含了侵彻过载信号曲线的大部分信号特征;分量2和分量3为高频噪声振动信号。对分量2和分量3进行频谱分析如图8所示,侵彻过载信号频谱如图9所示。 图8 分量2和分量3频谱图 图9 侵彻过载信号频谱图 由图8可知,分量2和分量3的频率集中点主要在1 072.7 Hz和3 875.4 Hz附近,与图9中的频率集中点1 061.1 Hz和3 863.9 Hz较为接近。因此,可认为侵彻过载信号经本文方法处理后,分离出的信号分量1与原信号的相似度约为95%,反映了弹体在侵彻过程中的刚体加速度特征;同时还分离出两个频率主要集中在1 072.7 Hz和3 875.4 Hz的高频振动信号分量2和分量3,由于弹体在侵彻过程中存在复杂的应力作用,因此这两个频率集中点可能为弹体的两次或多次谐振频率。 为了检验本文方法处理侵彻过载信号的可靠性和有效性,采用小波分解法和文献[5]中经验模态分解与独立分量分析法处理侵彻试验获得的侵彻过载信号,提取出的侵彻过载信号曲线如图10所示。 图10 三种方法提取出的侵彻过载信号曲线 由图10可知,本文方法分离的侵彻过载信号的曲线光滑度更高;文献[5]方法提取的侵彻过载信号在曲线快速上升和快速下降过程中存在曲线尖点问题;小波分解法提取的侵彻过载信号缺失部分细节特征,且该方法需人工选择小波基函数、分解层数和阈值,算法本身缺乏自适应性。为了进一步比较三种方法的侵彻过载信号特征分离效果,先对每条侵彻过载信号曲线分别在时域上进行一次积分,得到三条侵彻速度变化曲线,如图11所示;然后对每条侵彻速度变化曲线分别在时域上再进行一次积分,得到三条侵彻深度变化曲线,如图12所示。 图11 侵彻速度变化曲线 图12 侵彻深度变化曲线 由图11、12可知,本文方法得到的弹体触靶速度为485.9 m/s,弹体侵彻位移为100.61 cm;文献[5]中的方法得到的弹体触靶速度为458.7 m/s,弹体侵彻位移为97.18 cm;小波分解法得到的弹体触靶速度为465.5 m/s,弹体侵彻位移为98.44 cm。为了更直观地对比三种处理方法的处理效果,将三种处理方法得到的试验结果与实际侵彻数据进行对比,如表4所示。 表4 三种处理方法的试验结果对比 由表4可知,与文献[5]方法和小波分解法相比,本文方法得到的触靶速度和侵彻深度与侵彻试验数据的误差最小,所需处理时间最短,信号处理效率最高,因此本文方法具有更优的处理效果以及更高的可靠性和可行性。 变分模态分解能够自适应地将输入信号分解为若干个本征模态函数的线性组合,在保留信号局部特征规律的同时,有效去除了噪声信号,为单通道信号的盲源分离奠定基础。通过对本征模态函数的自相关矩阵进行奇异值分解并计算各本征模态函数与单通道观测信号的相关系数,将单通道观测信号转化为多通道观测信号,解决了欠定盲源分离中观测信号数目小于源信号数目的问题,然后由盲源分离中的JADE算法对重构的多通道观测信号进行分析处理。通过对分离的侵彻过载信号进行进一步分析处理,检验了本文方法的可靠性和可行性。与传统信号处理方法相比,本文方法具有以下优点: (1) 本文方法结合时频分析在非平稳信号分析中的优点,能够有效分离侵彻过程中作用在弹体上的多种频率响应,分离效果良好; (2) 盲源分离在混叠信号分离方面具有独特的优势,能够深入研究侵彻过程中作用在弹体上的复杂振动响应,挖掘出蕴含在复杂波形中的深层信息; (3) 本文方法很好地解决了欠定盲源分离中的源数估计问题,实现了侵彻过载信号的盲源分离。通过分析侵彻过载信号,得到侵彻过载信号的数据统计特征,挖掘其中蕴含的深层信息,从而分析弹体的侵彻过程,可为引信结构设计、弹体强度设计、防御工事的材料选择和结构设计提供重要参考依据。2.2 多通道观测信号盲源分离
3 侵彻试验分析
3.1 侵彻试验

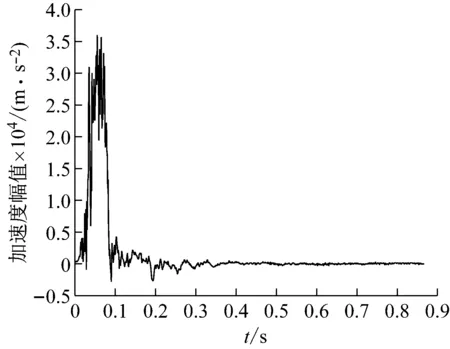
3.2 侵彻过载信号盲源分离
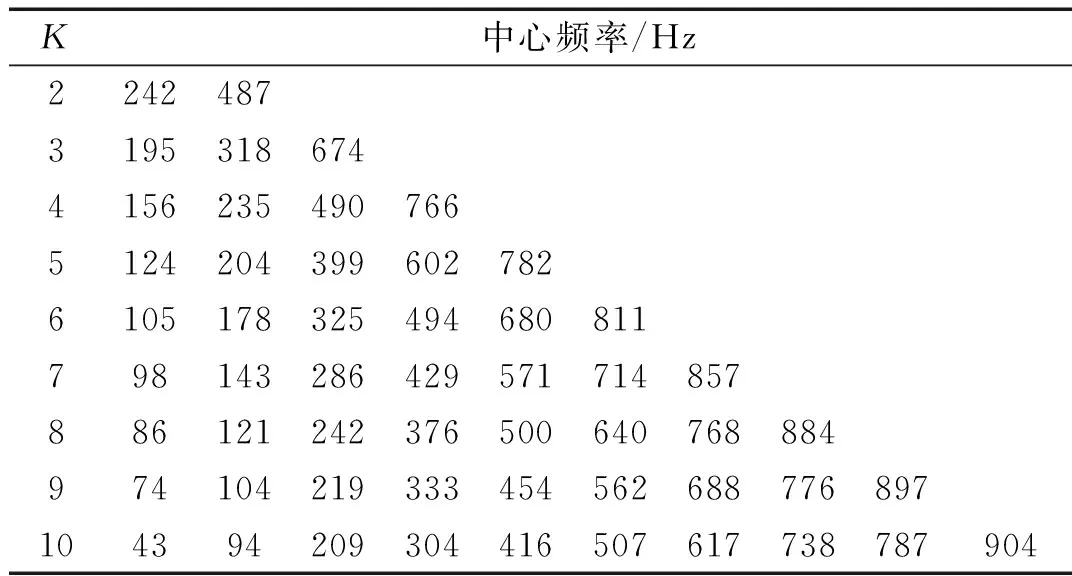
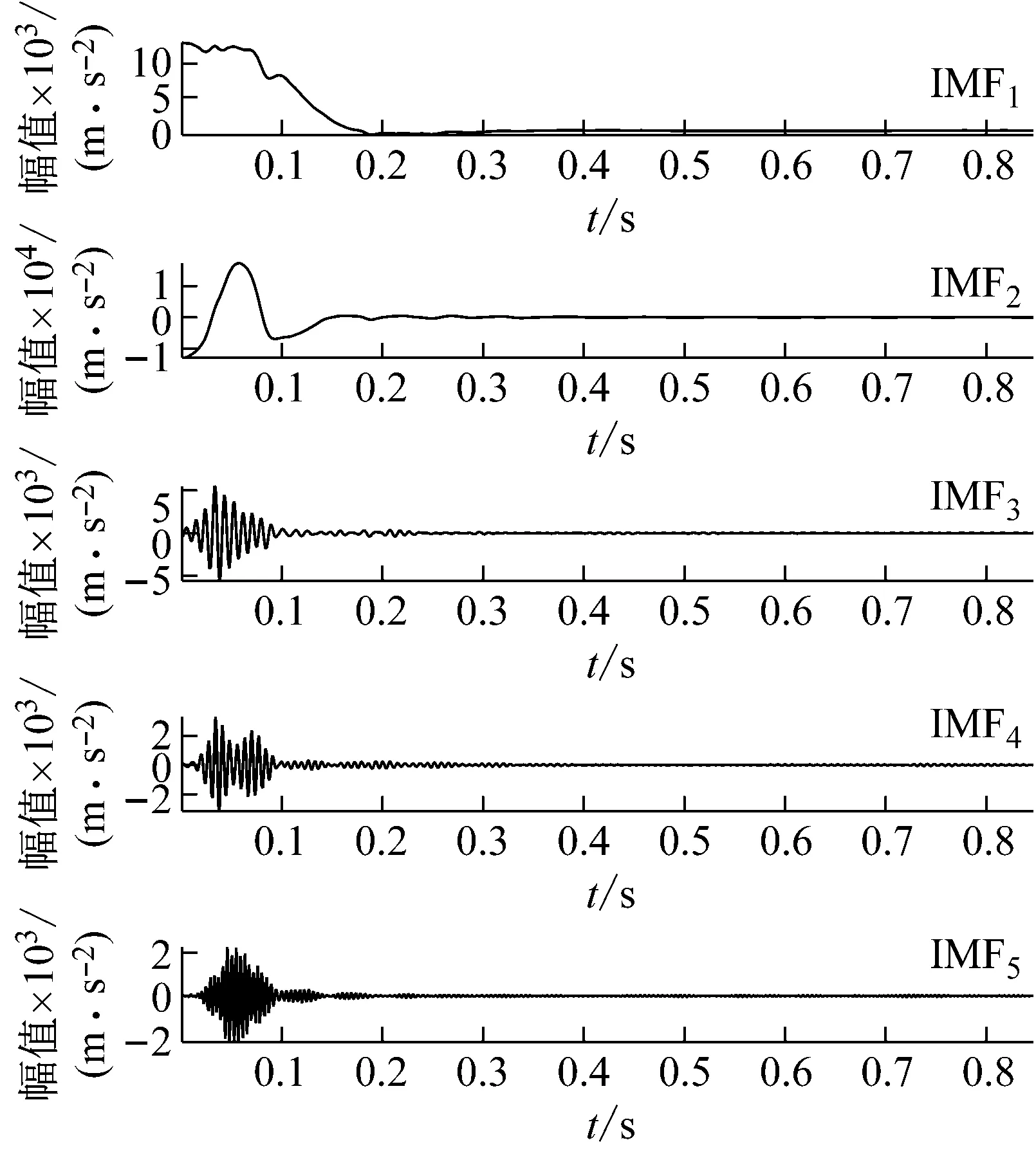
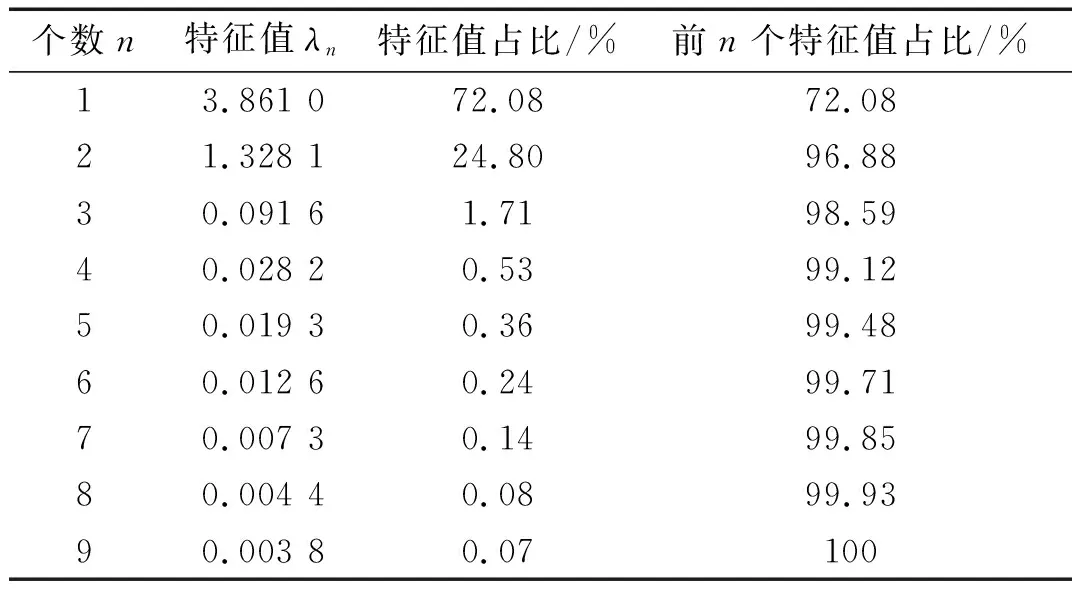
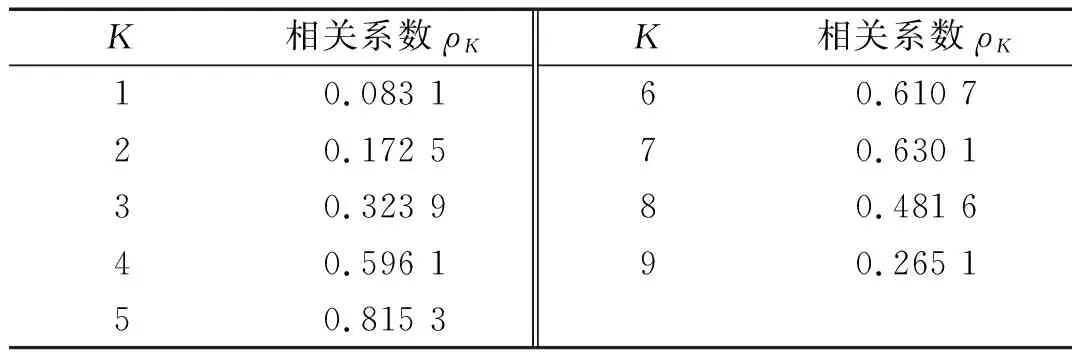
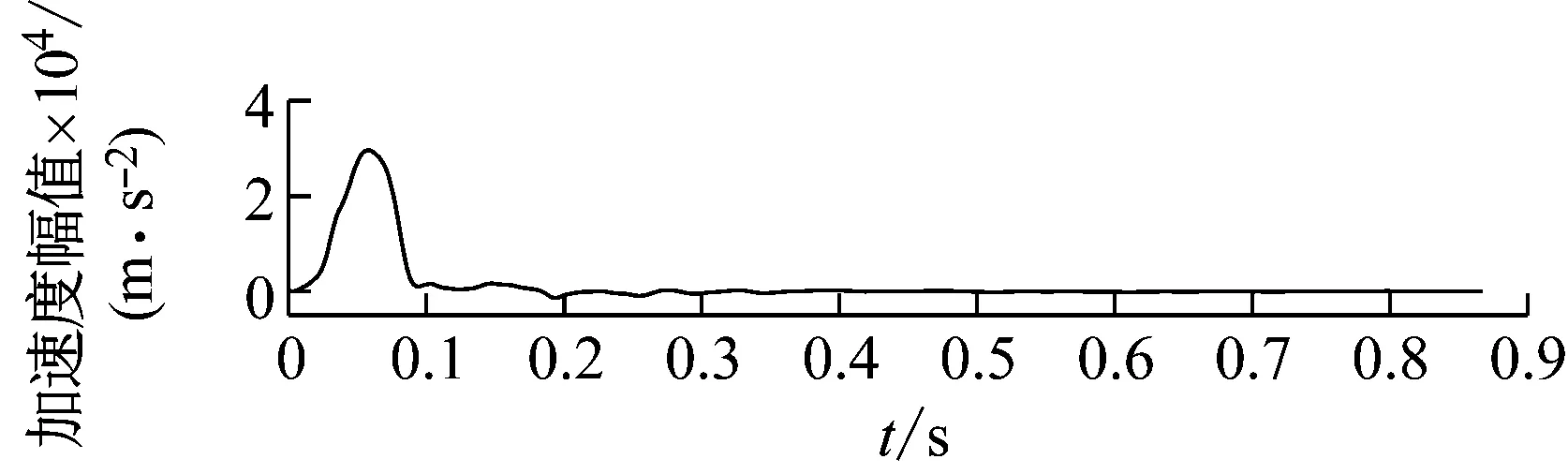
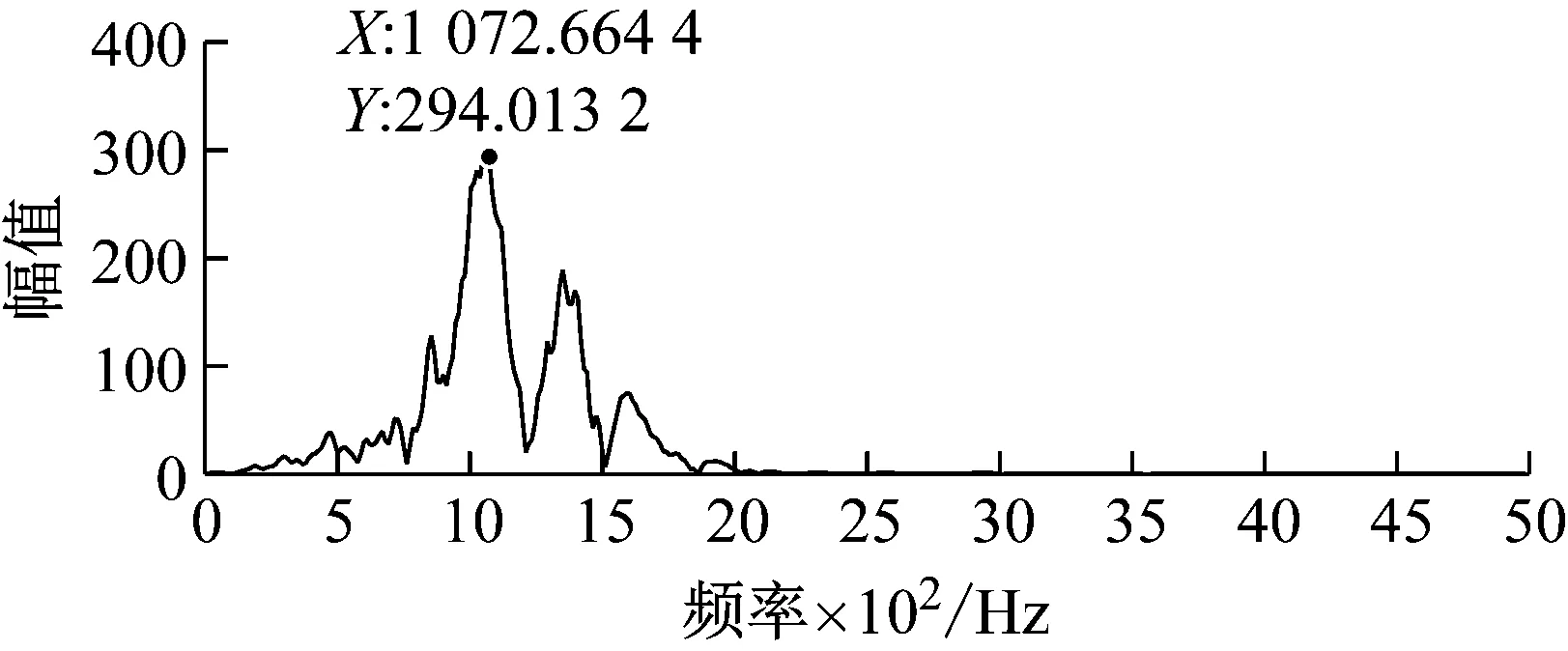
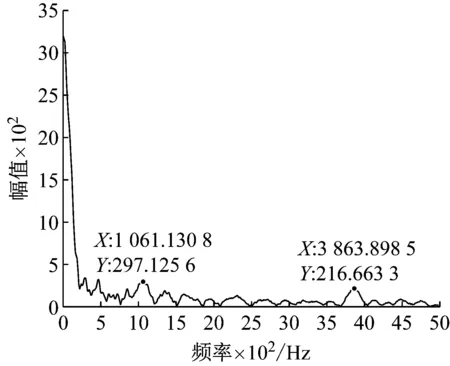
3.3 试验结果分析
4 结 论
