弹性胶泥缓冲器关键参数对快捷列车纵向冲动的影响

赵旭宝， 魏 伟， 董靓瑜， 李 静

(1.大连交通大学 计算机与通讯工程学院，大连 116028； 2.大连交通大学 机车车辆工程学院，大连 116028)

随着我国改革的不断深入，产业结构不断优化升级，“互联网+”及电商的快速发展，推动了以网络购物为代表的新型商务模式。以时效性、多样化、高附加值等特征的货物运输需求急剧增长。铁路货物运输模式正经历由数量需求向速度需求转变。快捷运输组织模式逐渐成为了当今世界铁路运输发展的重要方向。快捷货车以集装箱运输，日用百货、精密仪器、电子电器等高附加值货物运输为主，因此对运输的质量和速度有较高的要求。快捷铁路货车运行时速一般为140～160 km/h，列车编组20辆左右，牵引吨位为1 400～1 800 t[1]。从20世纪80年代开始，欧洲各发达国家，如德国、法国等，先后开发使用快捷货车。欧洲主要采用“编组短、质量轻、速度快”的轻捷快运模式。法国国家铁路公司，通过对货运繁忙干线全面提速和发展高速铁路货运等措施发展快捷运输。美国的快捷货运服务系统几乎覆盖了整个美洲大陆[2]。

由于快捷运输以运送高附加值货物为主，因此对其运输质量有较高的要求。缓冲器作为连接车辆的重要部件，在列车运行中起到了缓冲和耗散车辆纵向冲击动能的作用。缓冲器性能的优劣，直接影响着车辆间纵向力的大小，进而影响列车的纵向冲动。目前，在国内快捷货车上普遍使用的是弹性胶泥缓冲器，因此深入研究弹性胶泥缓冲器的关键参数对快捷列车纵向冲动的影响，对保障快捷货车运行的平稳性和安全性具有重要的意义。

Olshevskiy等[3]建立了改进的摩擦式缓冲器动力学模型和调车冲击的仿真模型。模拟了货车组的调车冲击工况，讨论分析了一车冲一车和多车冲多车工况下的缓冲器刚度和车钩力特性方面的主要区别。Wu等[4-5]建立了摩擦缓冲器、胶泥缓冲器和摩擦胶泥缓冲器三种具有不同阻尼机理的缓冲器模型，分析比较了三种缓冲器在货车冲击试验工况下的冲击特性、频率响应和疲劳损伤。Zhu等[6]建立了车钩缓冲器的力学模型，研究了城际列车冲击碰撞的机理。分析了车钩缓冲器对列车冲击碰撞行为的影响。研究了在碰撞过程中，车钩俯仰偏角的影响因素。Cole等[7-8]对货车用缓冲器进行了数学分析，建立了简化的缓冲器模型，研究了不同载荷下的重载列车纵向动力学性能。黄运华等[9]通过附加阻尼的方法构建摩擦式缓冲器模型，详细地研究了缓冲器的阻抗特性和列车纵向冲击机理；马卫华等[10]研究了摩擦胶泥型和弹性胶泥型缓冲器静态与动态阻抗特性对万吨重载列车动力学性能的影响；Chang等[11]利用描述悬挂系统中悬挂力的数学方程模拟了钢摩擦缓冲器实际的干摩擦阻尼迟滞特性，构建了重载列车纵向动力学模型。仿真分析了2万吨重载列车的纵向动力学特性，并用试验数据对仿真结果进行了验证。孙树磊等[12]以缓冲器动力学模型及空气制动系统模型为基础，建立了列车纵向冲击动力学模型，仿真分析重载组合列车在不同线路条件和制动作用下的纵向动力学行为。杨亮亮等[13]根据铁路货车纵向受力特点，利用MATLAB软件建立铁路货车调车冲击的动力学模型，研究了不同轴重车型，不同缓冲器特性、不同制动阻力状态及不同冲击模式对车辆纵向冲击特性的影响。张渊等[14]使用空气制动与纵向动力学联合仿真系统，计算万吨重载列车在回送运行施行紧急制动的列车纵向冲动。

但上述研究仅是针对重载列车纵向冲动，对快捷列车纵向冲动的分析，尤其是针对弹性胶泥缓冲器对列车纵向冲动研究较少，因此，本文根据弹性胶泥缓冲器的结构原理，构建一种基于速度型的弹性胶泥缓冲器动力学模型，利用空气制动与纵向动力学联合仿真系统，分析弹性胶泥缓冲器的各关键结构参数对列车纵向冲动的影响，找出其变化规律。

1 弹性胶泥缓冲器动力学模型

当前，在运行时速160 km/h的快捷货车上以JN30型弹性胶泥缓冲器应用最为广泛。该缓冲器主要是由缸体、环簧组件和弹性胶泥芯体等部分构成。总体结构如图1所示。

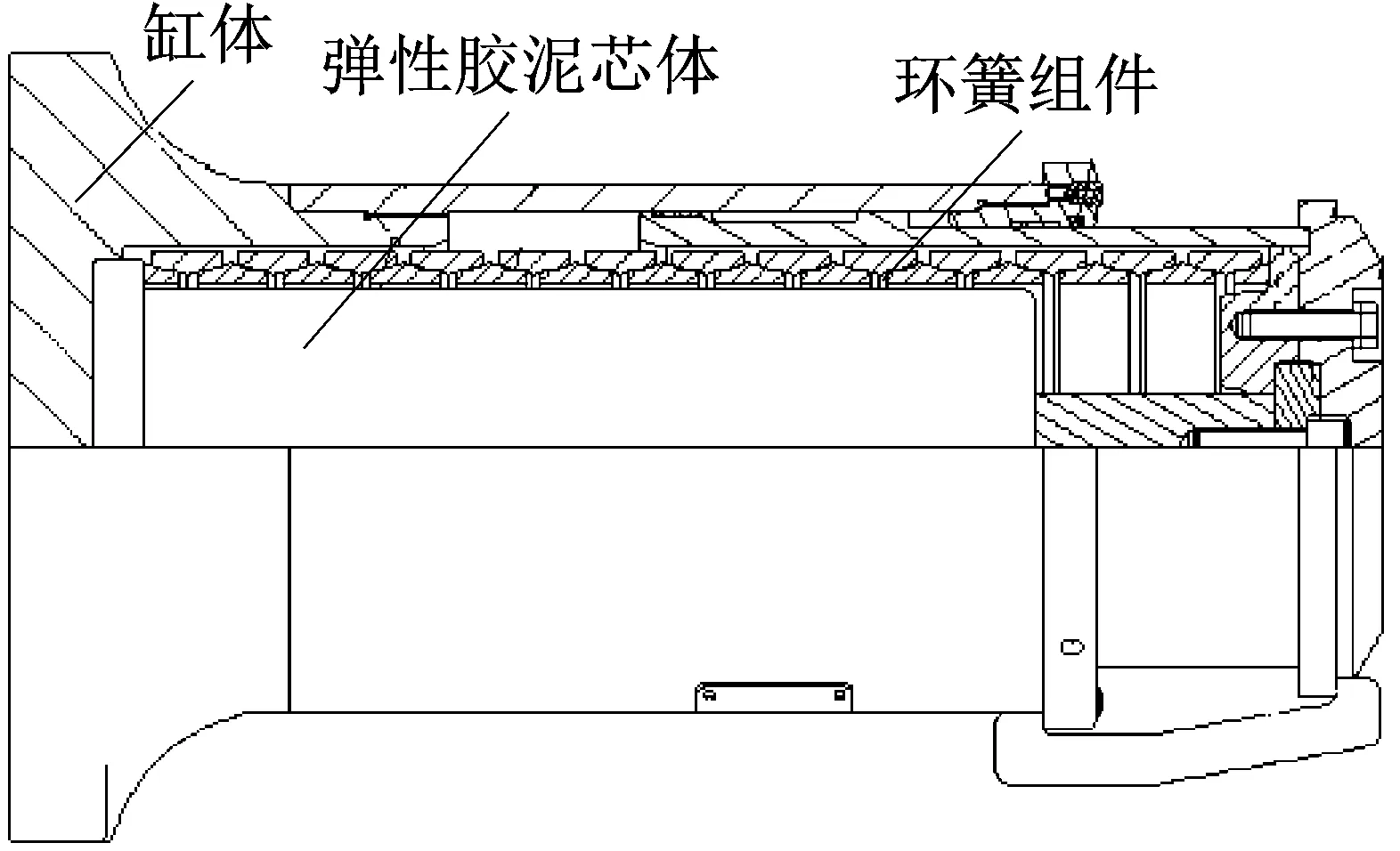
图1 弹性胶泥缓冲器总体结构图

弹性胶泥芯体是采用活塞杆导向、带高压室的双室结构，主要由缸体、活塞杆组件、弹性胶泥及密封装置等部分构成。其中弹性胶泥是由聚有机硅氧烷(简称聚硅氧烷)、填充剂等材料混炼而成，其主体材料聚硅氧烷是未经交联的，它决定了弹性胶泥的基本性能[15]。弹性胶泥芯体结构如图2所示。

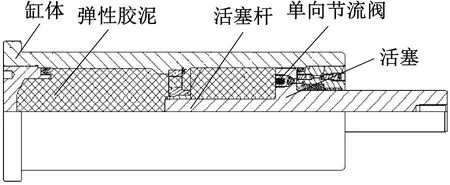
图2 弹性胶泥芯体结构图

弹性胶泥缓冲器在工作过程中是通过活塞杆的往复运动，弹性胶泥流体高速通过环状节流缝隙而产生阻尼作用力，利用弹性胶泥芯体和环簧组共同作用以缓和、吸收冲击能量。缓冲器在使用前会根据需要设置一定的预压力。缓冲器在受外力压缩时，活塞杆逐步压入活塞缸内，各环簧组开始相互挤压，产生弹性形变，环簧接触面间相互摩擦会消耗一定的冲击能量；同时活塞杆被压入缸体内，使得弹性胶泥体积压缩，增大了缸体内胶泥压力，从而给活塞杆提供了较大的反力，达到储能效果。由于胶泥具有良好的流动性，胶泥在活塞和缸体内壁间的环状缝隙内流动产生了阻尼力，同时吸收了大部分的冲击能量。缓冲器在复位时，环簧组作用力通过导套组成带动胶泥芯体同步复位。同时，胶泥从单向节流阀和活塞与缸体内壁间的环状缝隙回流到原来的腔室内，使得缓冲器回弹速度快、阻力小，保证了缓冲器及时复位。

由于缓冲器是由环簧组和弹性胶泥共同作用缓和列车纵向冲击能量。因此，缓冲器既具有黏滞耗能特性，又具有弹性储能特性，能够自复位。因此，本文假设缓冲器阻抗力仅由弹性力和胶泥阻尼力构成。缓冲器的动力学模型看作是由一带刚度的弹性元件和一随速度变化的阻尼元件组成。缓冲器动力学模型方程可表示为式(1)

F=F0+Fk+Fd

(1)

式中：F为缓冲器总的阻抗力；F0为缓冲器的初压力；Fk为弹性元件的弹性力；Fd为阻尼元件的阻尼力。

在缓冲器的工作过程中，缓冲器的弹性回复力，主要来自两个方面，其一是环簧组的弹性回复力；其二是缸体内胶泥的弹性回复力。等效的弹性回复力表示为式(2)

Fk=a1·Δx

(2)

式中：α1为缓冲器加载过程中弹性力对应的综合等效刚度；Δx为缓冲器位移。

另外，由于弹性胶泥属于一种剪切稀化流体[16]，根据其本构关系方程和活塞杆的结构，推导出胶泥的阻尼力如式(3)

Fd=c·vn

(3)

式中：c为与活塞杆结构相关的系数；n为胶泥的流动指数，反映胶泥材料非牛顿流体性质的强弱，其取值范围为0～1，对于某一固定型号的胶泥n为常数，n值可以通过试验测得。

2 空气制动与纵向动力学联合仿真系统

根据列车纵向动力学原理和气体流动理论，大连交通大学开发了列车空气制动与纵向动力学联合仿真系统(TABLDSS)[17]。该系统具有同步仿真列车制动特性和纵向动力学特性的功能。系统还具有良好的牵引特性、制动特性、车钩力、加速度等性能参数同步计算及图形化显示功能。系统可模拟司机根据线路状况、运行速度、列车限速等因素控制列车真实的运行过程。该系统为分析列车纵向冲动机理、优化制动特性、优化缓冲器特性、模拟列车驾驶提供了基本理论和实用工具。该仿真系统曾参加了国际列车纵向动力学模拟器的基准测试[18]。此项活动共有6个国家的9款仿真系统参与测试，TABLDSS仿真系统针对每个算例的计算精度和计算速度都名列前茅。

3 弹性胶泥缓冲器关键参数对快捷列车纵向冲动的影响分析

在列车正常运行状态下，列车以实施紧急制动时产生的纵向冲动最为严重。因此，本文重点分析列车在紧急制动情况下，列车的纵向加速度和车钩力两个性能参数的变化。以此来分析缓冲器关键参数对列车纵向冲动的影响。

仿真计算条件：列车组成为1+20(1辆SS9电力机车+20辆P160D快运棚车)，单节车重72 t。在平直线路上，以160 km/h初速度实施紧急制动。制动系统采用KZ1快充分配阀，10 mm车钩间隙。

3.1 初压的影响

根据本文建立的弹性胶泥缓冲器模型，当其他参数不变时，将式(1)中缓冲器模型的初压力值分别调整为20 kN,40 kN,60 kN,80 kN,100 kN等值。考察缓冲器初压力变化对列车纵向冲动的影响。仿真计算结果如图3和图4所示。

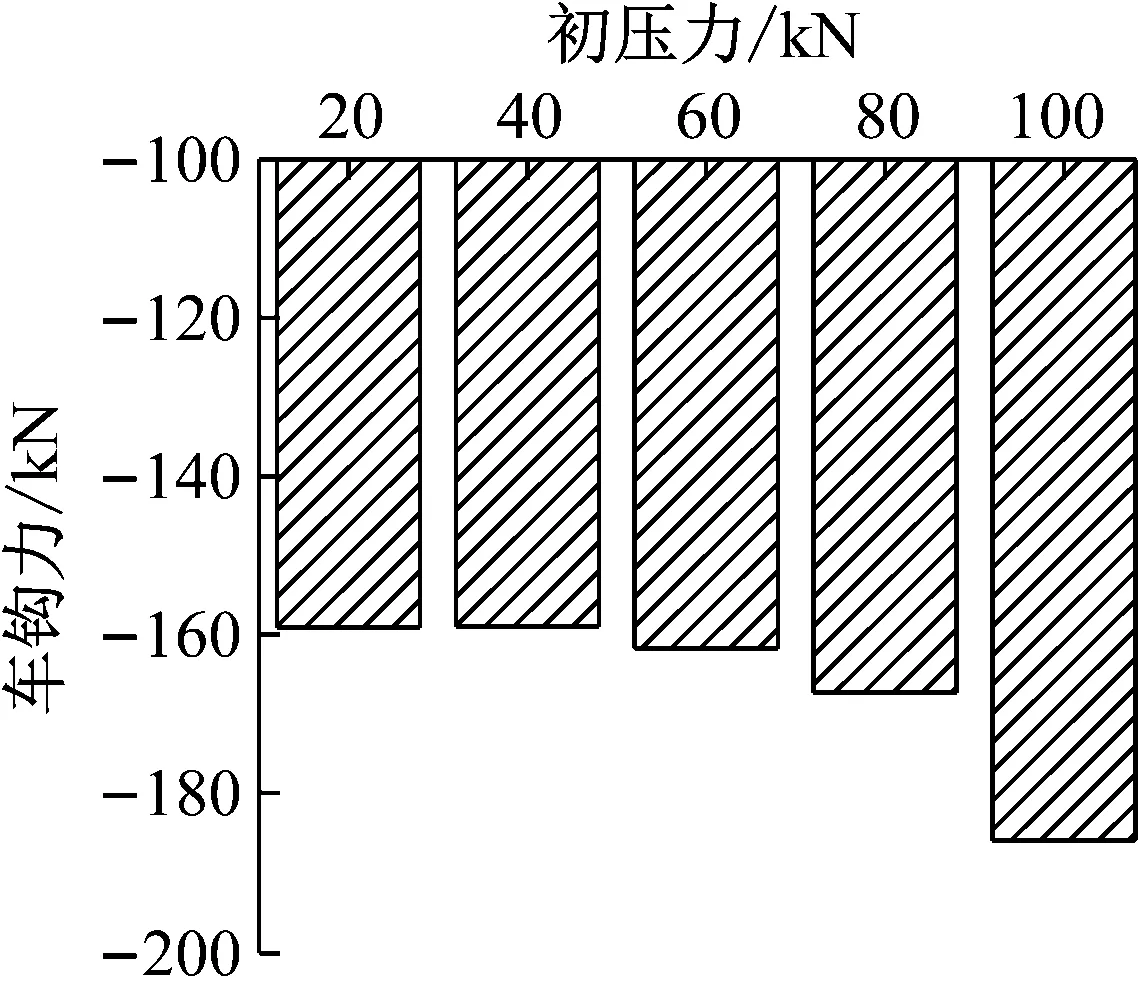
图3 初压力对最大车钩力的影响

图4 初压力对最大加速度的影响

图3,4分别给出了在不同初压力情况下列车最大车钩力(压钩力)和最大加速度值的变化。由图3可以看出随着初压力的不断增大，车钩力呈非线性增大，但在初压力小于60 kN范围内，车钩力变化较小。在初压力为20 kN时，列车中最大车钩力为-159.1 kN；初压力为100 kN时，列车中最大车钩力为-185.9 kN。初压力由20 kN 增大到100 kN时，车钩力增长 14.4%。由图4可知，在初压力小于40 kN范围内，加速度值随着初压的增大有逐渐变小的趋势，但变化幅度较小；在初压力大于40 kN范围内，加速度值随初压力增加而增大。初压力为100 kN时，列车中最大加速度为-2.43 m/s2。初压力由20 kN 增大到100 kN时，加速度增长了32.9%。由此表明，缓冲器的初压力设置过大将会增大列车的纵向冲动。分析其原因是增大初压相当于增大缓冲器的初始阻抗，在车钩力由前向后传递过程中，使得相邻两车辆间的车钩力差增大，最终导致车钩力和加速度随初压的增加而增大。综合车钩力与加速度的变化趋势可知，缓冲器的初压力设置在40 kN左右较为合理。图5和图6进一步给出了列车在不同初压情况下最大车钩力与加速度沿车长的分布。

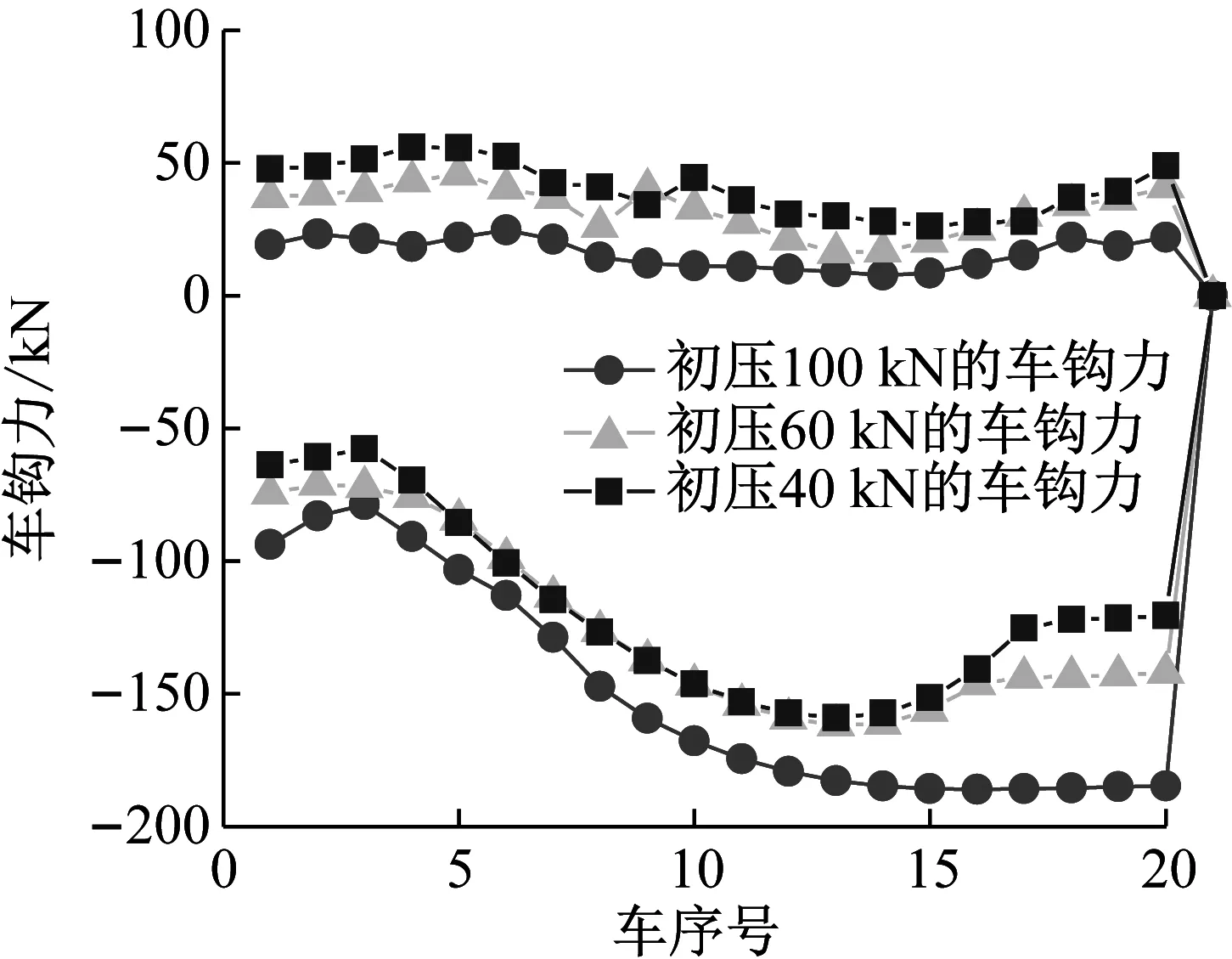
图5 车钩力最大值沿车长的分布

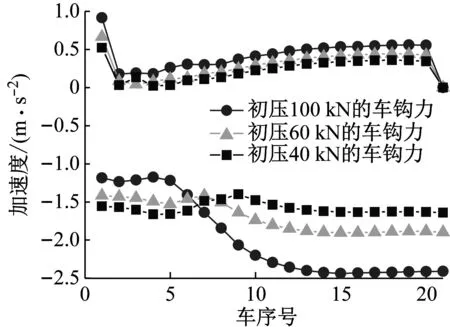
图6 加速度最大值沿车长的分布

3.2 综合等效刚度的影响

根据环簧组的静压试验可知，环簧的等效刚度约为2.4 kN/mm，环簧组静压试验结果如图7所示。同时考虑弹性胶泥在流动过程中也具有一定的刚度，因此本文在弹性胶泥缓冲器模型中，将式(2)中综合等效刚度分别设定为3,4,5,…,10等值。考察缓冲器环簧机构等对应综合等效刚度的变化对列车纵向冲动的影响。仿真计算结果如图8和图9所示。

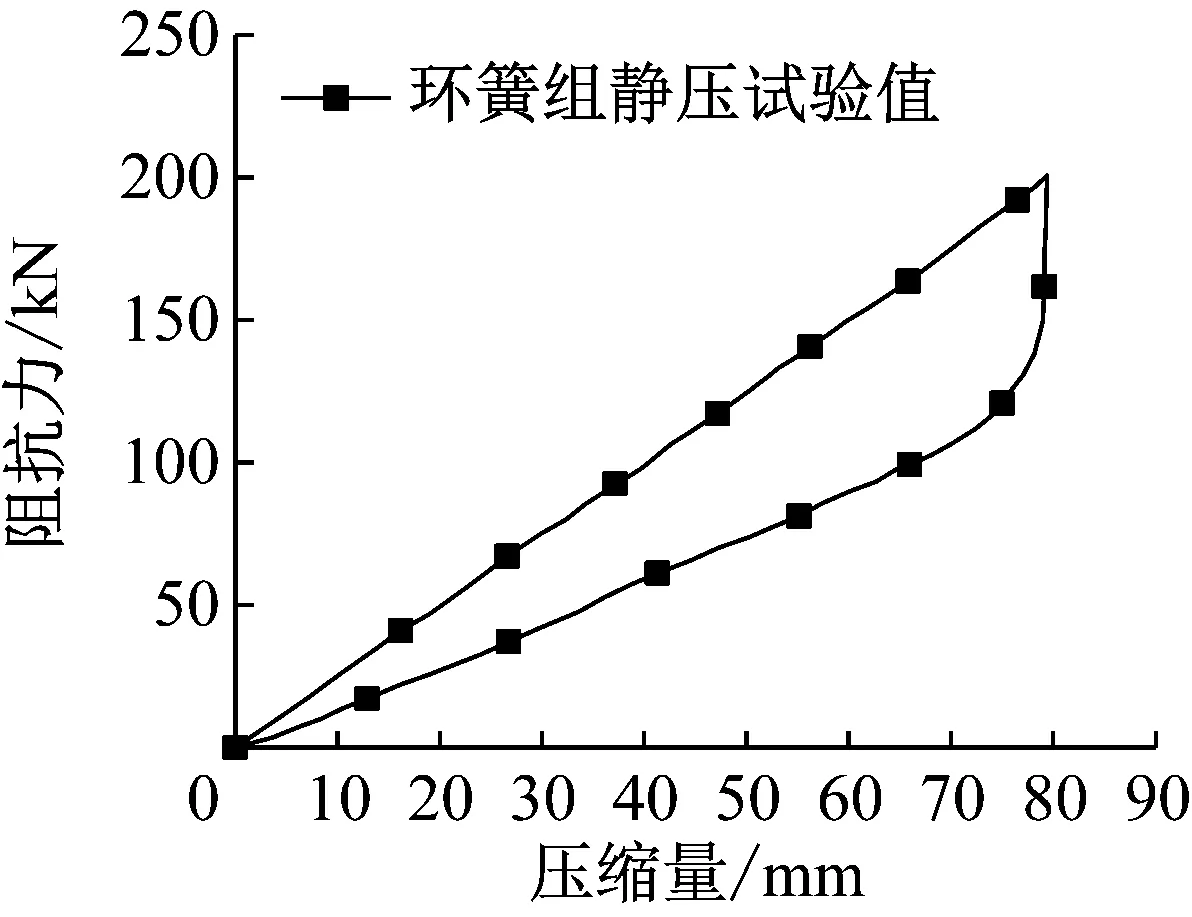
图7 环簧组静压试验结果

图8 综合等效刚度对列车最大车钩力的影响

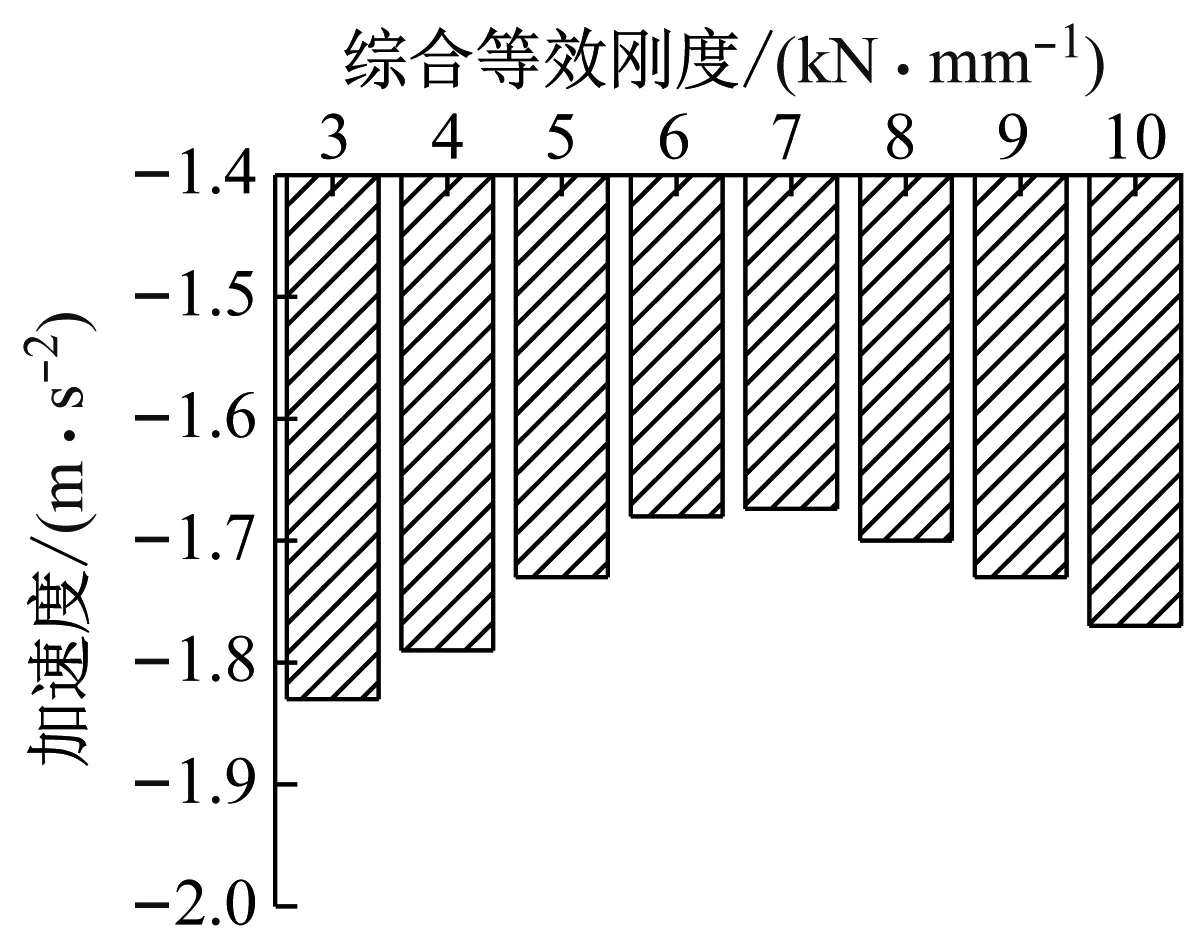
图9 综合等效刚度对列车最大加速度的影响

图8,9给出了不同综合等效刚度下的列车车钩力(压钩力)和加速度的最大值的变化规律。由图8,9可以看出，随着综合等效刚度的增大，列车车钩力最大值有逐渐增大的趋势，当等效刚度设定为3 kN/mm时，车钩力最大值为-131.18 kN；当等效刚度设定为10 kN/mm时，车钩力最大值为-174.92 kN，但变化幅度仅为43 kN。在综合等效刚度逐渐增大的过程中，列车加速度最大值呈现了先变小后逐渐增大的变化过程，但变化的幅度为仅为7.2%，最大的加速度值为-1.83 m/s2。由此表明，综合等效刚度对列车纵向冲动有一定的影响，但影响较小。分析其原因是综合等效刚度大小仅影响缓冲器的弹性回复力，而根据缓冲的工作原理可知，在弹性胶泥缓冲器中，缓冲器的性能主要是由弹性胶泥的性质所决定，弹性回复力对缓冲器的性能影响较小，因此车钩力和加速度受其影响较小。图10,11给出了不同等效刚度下沿车长分布的车钩力和加速度。

图10 车钩力最大值沿车长分布

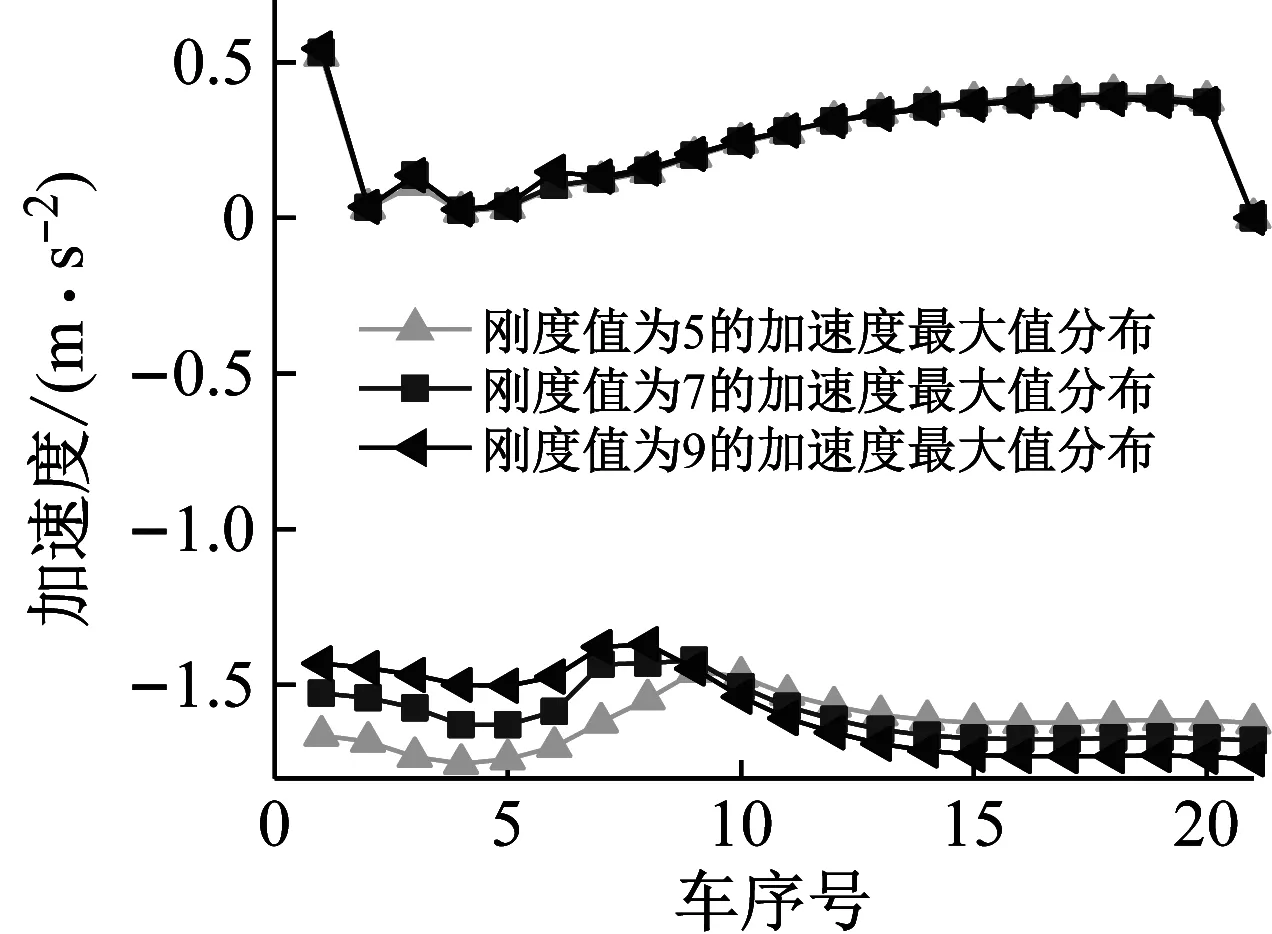
图11 加速度最大值沿车长分布

3.3 胶泥流动指数的影响

在缓冲器模型中，在保持其他参数不变的情况下，将式(3)中胶泥流动指数n分别调整为0.1,0.2,…,0.9等值进行仿真计算，分析流动指数对列车纵向车钩力和加速度的影响。仿真计算结果如图12和图13所示。

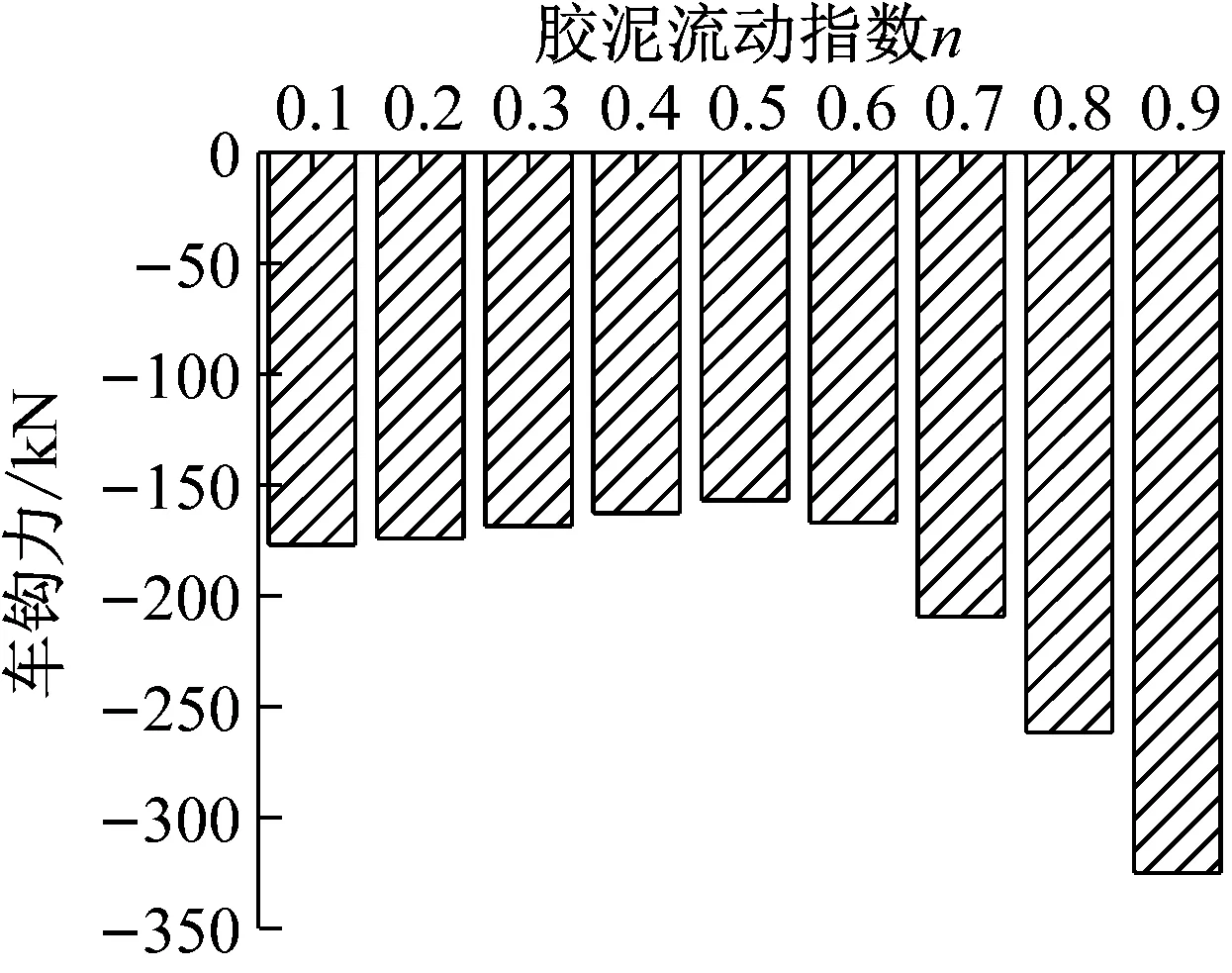
图12 胶泥流动指数对最大车钩力的影响

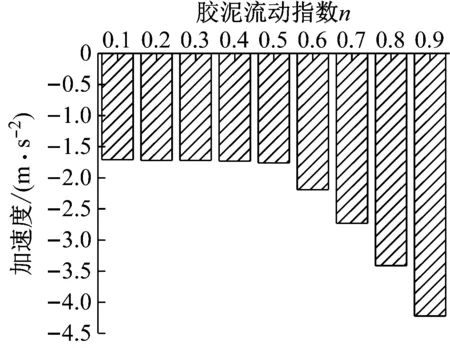
图13 胶泥流动指数对加速度的影响

图12,13给出了在不同胶泥流动指数情况下的列车车钩力(压钩力)和加速度最大值的变化趋势。由图可12,13可知，胶泥流动指数对列车的车钩力和加速度影响较大。尤其是当n大于0.5时，车钩力和加速度呈指数级增长。当胶泥指数在0.1～0.5内变化时，车钩力随流动指数的增大呈逐渐减小的趋势，但车钩力整体变化幅度较小，仅为20.1 kN。在这个范围内列车加速度最大值基本无变化。当胶泥指数在0.5～0.9内变化时，车钩力和加速度都随流动指数的增加而增大。在n值为0.5和0.9时，车钩力最大值分别为-156.8 kN和-324.9 kN，增幅为51.7%；加速度最大值分别为-1.7 m/s2和-4.2 m/s2，变化幅度为59.5%。其原因是弹性胶泥缓冲器属于速度型耗能器。由式(3)可知，阻尼力的大小与冲击速度的幂次方(即流动指数n)成正比，因流动指数为正数且小于1，所以阻尼力随活塞杆移动速度的增大而增加，但增长幅度逐渐减小。这正是胶泥缓冲器优点的体现。当冲击速度较小时，缓冲器能提供较大的阻尼力，而冲击速度较大时，又能较好的抑制阻尼力的最大值。这样对车辆起到了很好的保护作用。但根据式(3)，当流动指数n较小时，提供的阻尼力也相对较小；相反，当n较大时，提供的阻尼力相对也较大。最终导致车钩力和加速度受流动指数n影响较大。由上述分析可知，胶泥的流动指数限定在0.5附近时，将有助于降低列车的纵向冲动。图14,15给出了在不同胶泥流动指数情况下车钩力和加速度沿车长变化情况。

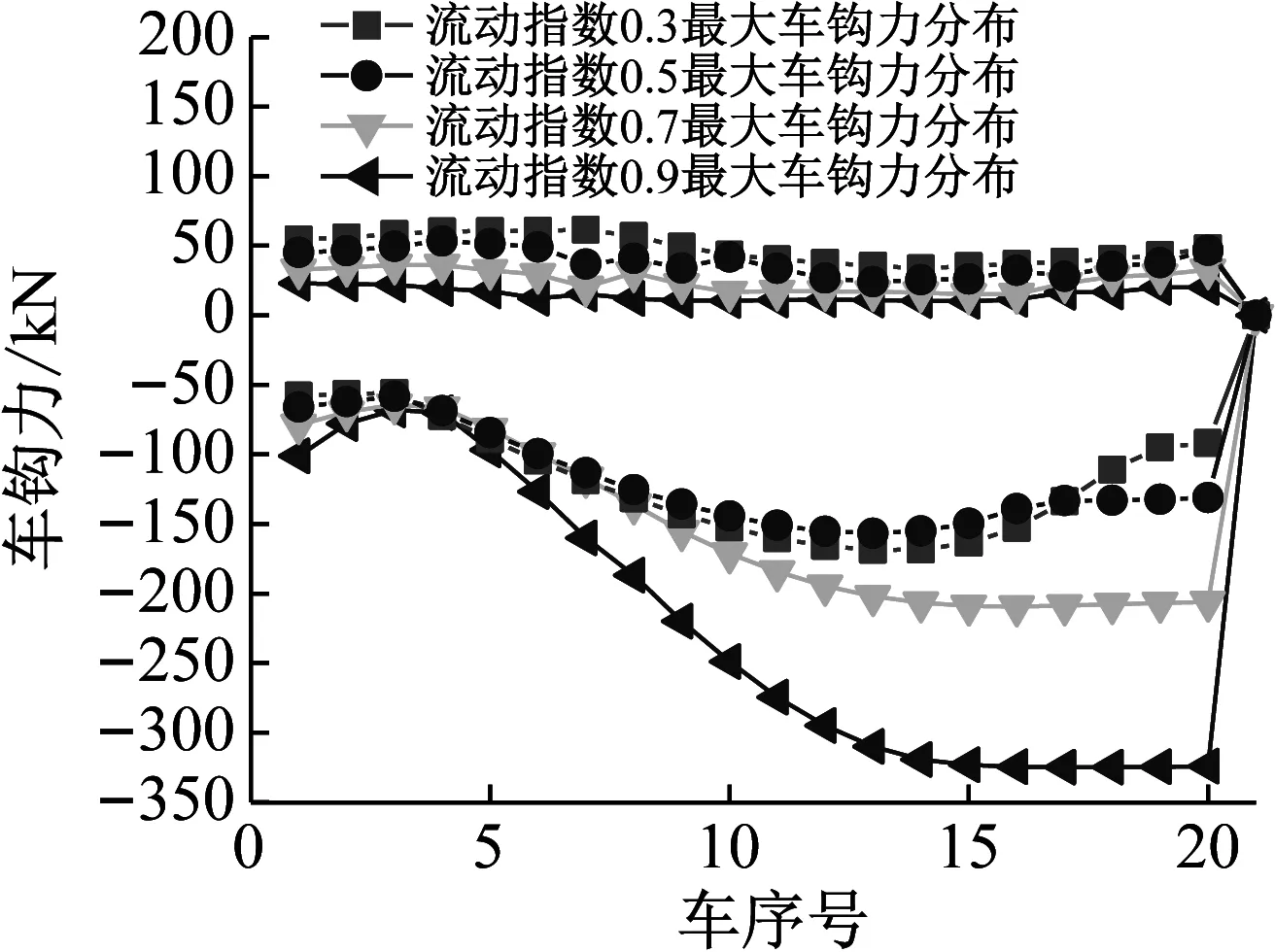
图14 车钩力最大值沿车长分布

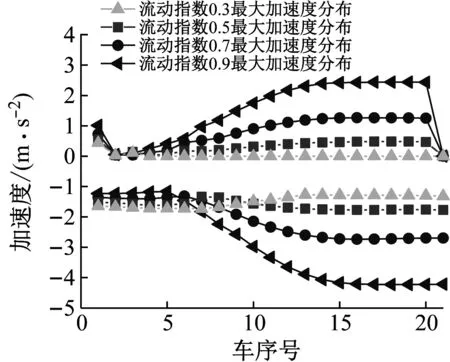
图15 加速度最大值沿车长分布

4 结 论

本文根据弹性胶泥缓冲器的结构原理，建立了基于速度型的弹性胶泥缓冲器模型，利用空气制动与纵向动力学联合仿真系统，分析了快捷货车在初速度为160 km/h时的平道紧急制动工况下，缓冲器模型关键参数变化对列车纵向冲动的影响规律。得出结论如下：

(1) 随着缓冲器初压力的不断增大，车钩力和加速度均呈非线性增大趋势。初压力由20 kN 增大到100 kN时，列车车钩力最大值增长了14.4%；加速度最大值增长了32.9%。综合车钩力与加速度的变化趋势可知，过大的缓冲器初压力将会增大列车的纵向冲动。缓冲器的初压力设置在40 kN左右较为合理。

(2) 与缓冲器环簧组相关的综合等效刚度对列车的纵向冲动有一定的影响，但影响较小。

(3) 弹性胶泥的流动指数对列车的最大车钩力和最大加速度影响最大。尤其是当n大于0.5时，车钩力和加速度呈指数级增长。当胶泥指数在0.1～0.5内变化时，车钩力随流动指数的变化幅度较小，而在这个范围内列车加速度最大值也基本无变化。但当胶泥指数在0.5～0.9内变化时，车钩力和加速度均随流动指数的增加呈指数级增长。胶泥流动指数在0.5～0.9内变化时，车钩力最大值增大为51.7%；加速度最大值增幅为59.5%。根据仿真结果，将胶泥的流动指数限定在0.5左右为宜，既可以保障缓冲器有足够大的缓冲能力，又能降低快捷列车的纵向冲动。