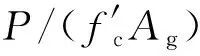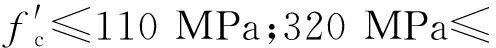钢筋混凝土矩形柱地震破坏模式的概率分析
2022-03-18程学斌吕瑞晗许新勇张建伟
马 颖, 程学斌, 吕瑞晗, 许新勇, 张建伟
(1.华北水利水电大学 水利学院,郑州 450046;2.中国地震局建筑物破坏机理与防御重点实验室,河北 三河 065201;3.中国电建集团北京勘测设计研究院有限公司,北京 100024)
在地震作用下,钢筋混凝土柱作为竖向承载构件,同时也承受水平侧向力。随着配筋率和剪跨比的变化,钢筋混凝土柱通常会发生弯曲、弯剪或剪切破坏[1]。震后调查研究表明,不同破坏模式的性质不同,钢筋混凝土柱的抗震性能迥异[2-3]。而钢筋混凝土柱的抗震性能直接影响建筑物或桥梁结构的易损性和安全性评估。特别是剪切破坏, 纵筋不能屈服呈现完全的脆性特征,不能通过能量耗散支撑整个结构的安全,此破坏模式在抗震设计时必须避免。此外,对于纵向钢筋屈服后变形能力不如弯曲破坏的弯剪破坏,设计中也要控制。因此,在基于性能的抗震设计和安全评估中,识别钢筋混凝土柱的破坏模式是很重要的。
目前对钢筋混凝土柱的弯曲破坏机理的认识已经较为深入,经典的纤维梁柱单元模型已被广泛应用[4-8]。然而,由于剪力作用机理较为复杂,对于剪切或弯剪破坏的破坏机理研究尚不足,还没有完全合理的理论计算模型描述这两种破坏特征[9-11]。因此,仅根据破坏机理来识别钢筋混凝土柱的破坏模式仍存在部分困难。
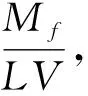
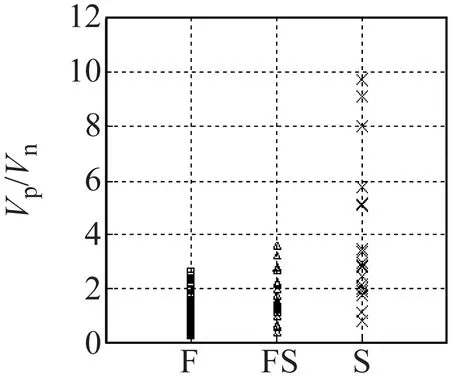
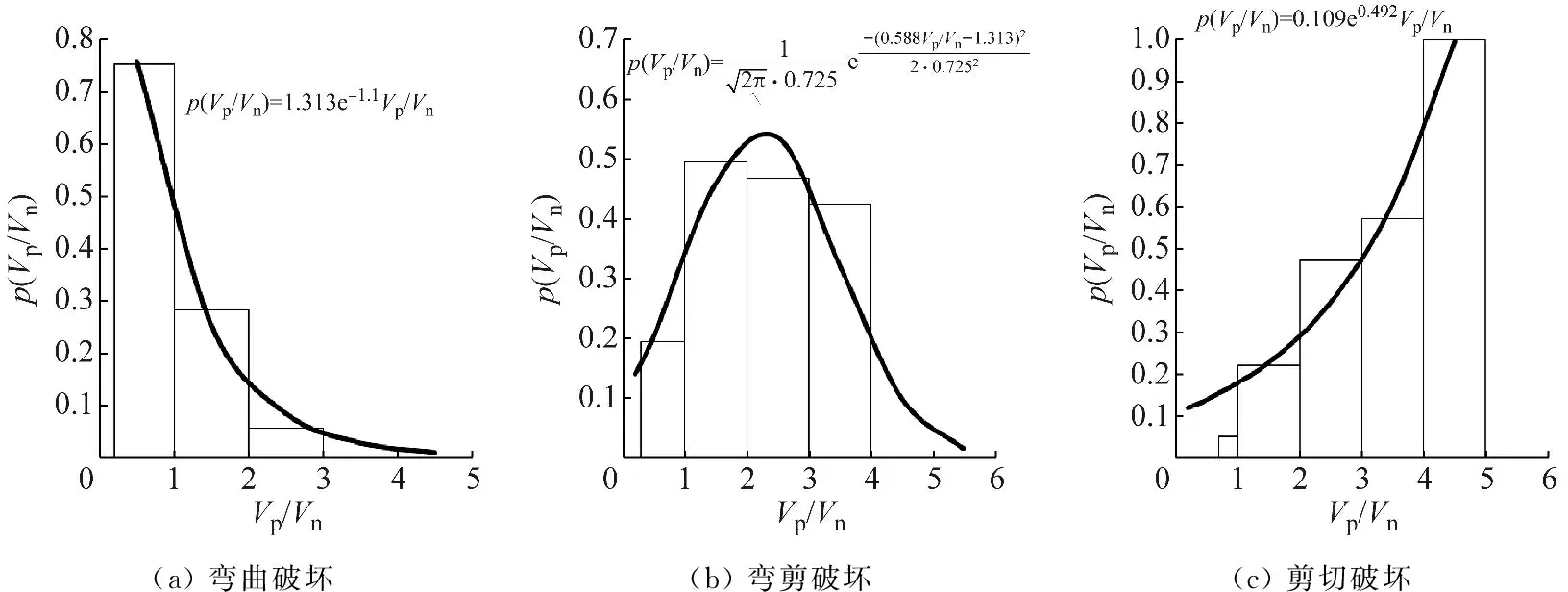
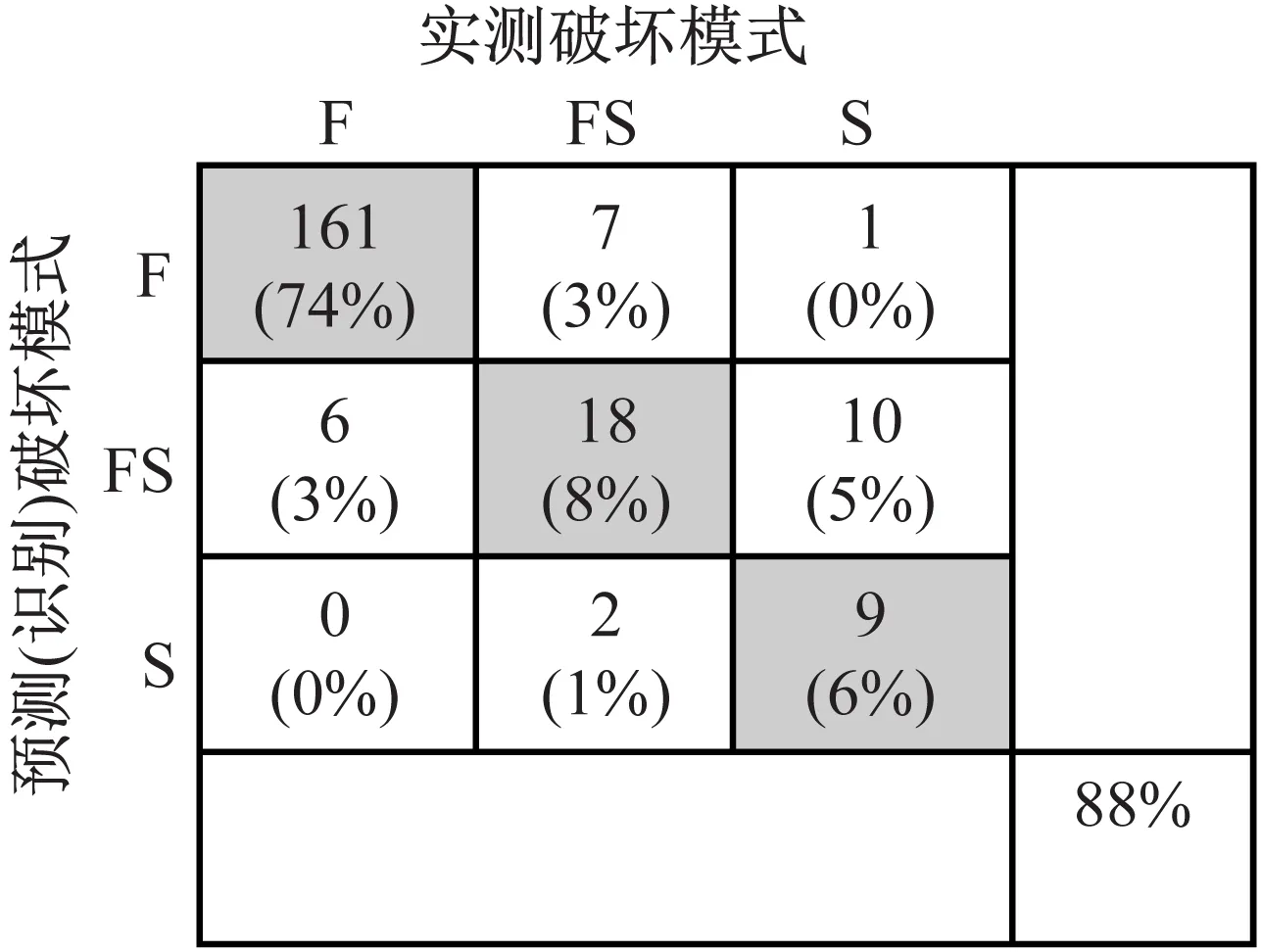
本文分析了钢筋混凝土柱发生弯曲、弯剪和剪切三种破坏模式的破坏特征及影响因素。根据柱塑性铰区截面的剪力需求与抗剪承载力的关系,计算了三种破坏模式的剪力需求与抗剪强度的比值,并分别给出了相应的概率分布函数。
1 地震破坏模式
根据钢筋混凝土柱塑性铰区截面的剪力需求和抗剪承载力(Vp/Vn)之间的关系,地震荷载作用下柱发生弯曲、弯剪和剪切破坏的理论定义如图1所示。
如果抗弯承载力所对应的剪力需求始终处于抗剪承载力曲线下方,即荷载-变形曲线和抗剪承载力包络线始终没有相交,柱试件发生弯曲破坏,如图1“a”曲线所示。弯曲破坏柱通常表现出较好的转动能力和位移延性,首先纵向钢筋屈服形成塑性铰,随着变形增大,裂缝不断发展,混凝土保护层剥落,最后核心混凝土达到极限压应变压碎破坏。整个过程吸收较大的地震能量,属于延性破坏。
如果抗弯承载力所对应的剪力需求介于初始抗剪强度和残余抗剪强度之间,柱试件在抗剪强度和荷载-变形曲线相交处时发生弯剪破坏,如图1“b”曲线所示。弯剪破坏柱在破坏之前表现出稳定的弯曲特性,并表现出一定程度的位移延性和能量耗散。纵向钢筋屈服后,侧向承载能力随着变形的增大而降低,而柱的破坏正是由柱的抗剪强度降低而引起的。
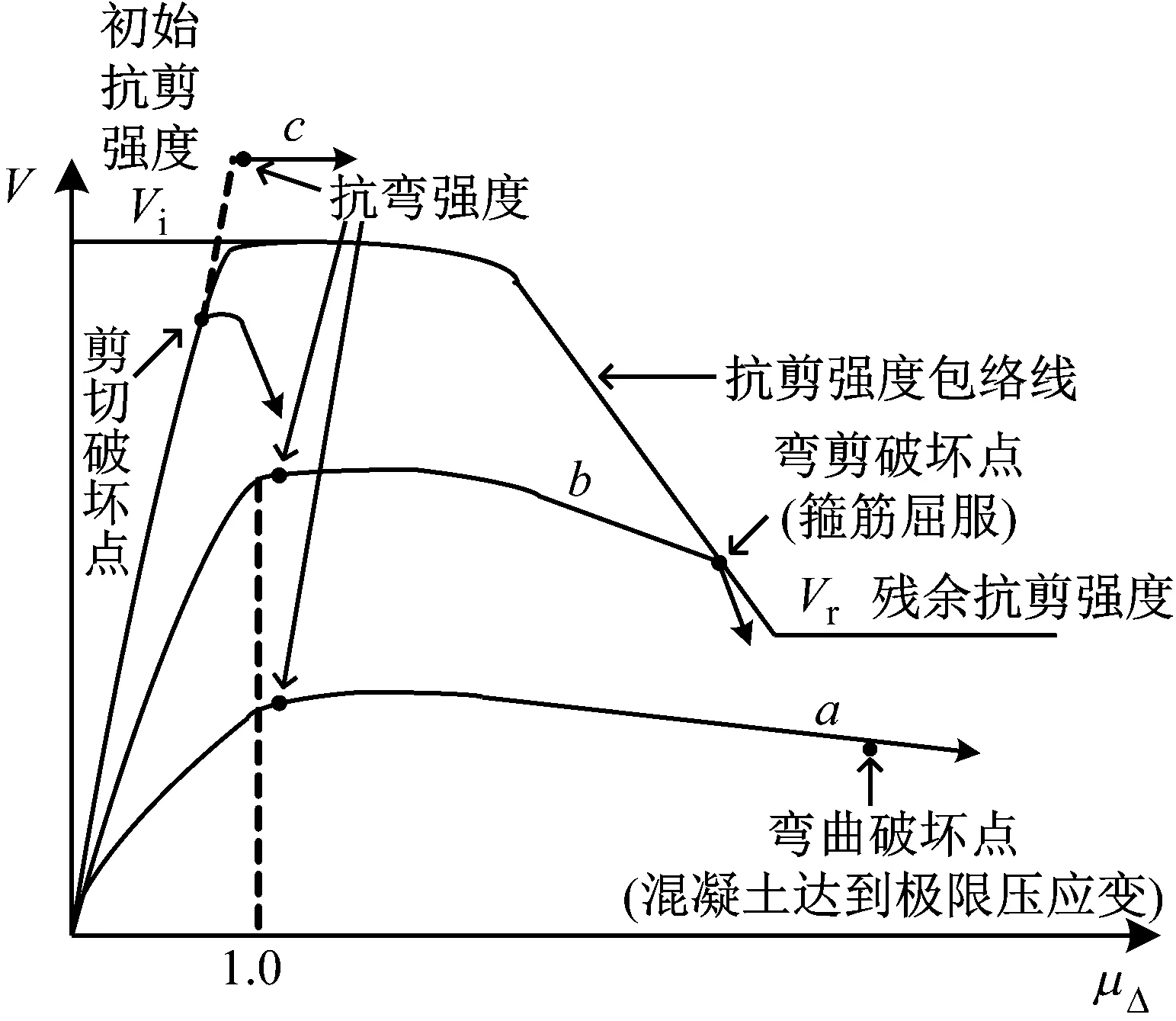
图1 钢筋混凝土柱不同破坏模式的荷载-变形曲线
如果抗弯承载力所对应的剪力需求大于初始抗剪强度,柱试件发生剪切破坏,如图1“c”曲线所示。由于斜裂缝发展迅速,在纵向钢筋屈服之前,箍筋屈服发生脆性破坏。柱的剪切破坏位移小于柱的屈服位移,几乎没有塑性变形能力。
因此,钢筋混凝土柱的三种破坏模式表现出一定的相似性和差异性。弯曲和弯剪破坏的共同特征是塑性铰区的纵向钢筋首先屈服,然后纵向钢筋处于塑性流动状态。最后,受压区边缘混凝土达到极限压缩应变。在边缘混凝土达到极限应变之前,如果抗剪强度退化直至剪力需求,则发生弯剪破坏,否则发生弯曲破坏。弯剪破坏柱的延性小于弯曲破坏柱的延性。剪切和弯剪破坏的差异是,对于剪切破坏柱,在纵向钢筋屈服之前,剪力需求大于初始抗剪强度;而对于弯剪破坏柱,纵向钢筋首先屈服,然后抗剪强度随着变形的增加而降低。
2 地震破坏模式的影响因素分析
2.1 试验数据
本文采用了美国太平洋地震研究中心钢筋混凝土柱抗震性能试验数据库(PEER-Structural Performance Database)中214根矩形截面柱的试验数据。对于每根柱试件,PEER提供了柱试件的几何尺寸、材料强度、加载方式、破坏模式和荷载-变形曲线等。试件的基本参数范围如下:
·纵筋屈服强度:318 MPa≤fy≤587.1 MPa
·纵筋配筋率:0.68%≤ρl≤6.03%
·箍筋屈服强度:249 MPa≤fyv≤1 424 MPa
·体积配箍率:0.1%≤ρsv≤6.74%
·剪跨比:1≤a/h≤7.368
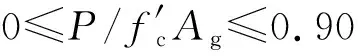
·箍筋间距与截面高度比:0.1≤s/h≤1
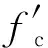
2.2 影响因素分析
影响钢筋混凝土柱抗震破坏的因素有几何尺寸、材料强度、配筋情况、外加荷载等。本文选取箍筋和纵筋配筋率、混凝土和钢筋的强度、剪跨比和轴压比进行影响因素分析。在分析中,符号F、FS和S分别表示弯曲、弯剪和剪切破坏。
2.2.1 箍筋
地震作用下,构件配置足够的箍筋,可以限制斜裂缝的宽度和发展,提高斜截面的骨料咬合作用,阻止混凝土沿纵筋的撕裂,增加对核心混凝土的约束作用。而且可以限制混凝土向外膨胀,提高核心混凝土的极限应变,增加构件的延性,从而有效地改善构件的破坏模式和抗震性能。
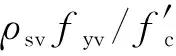

图2 箍筋配置对柱试件破坏模式的影响
2.2.2 纵筋
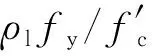
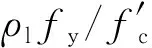

图3 纵筋配置对柱试件破坏模式的影响
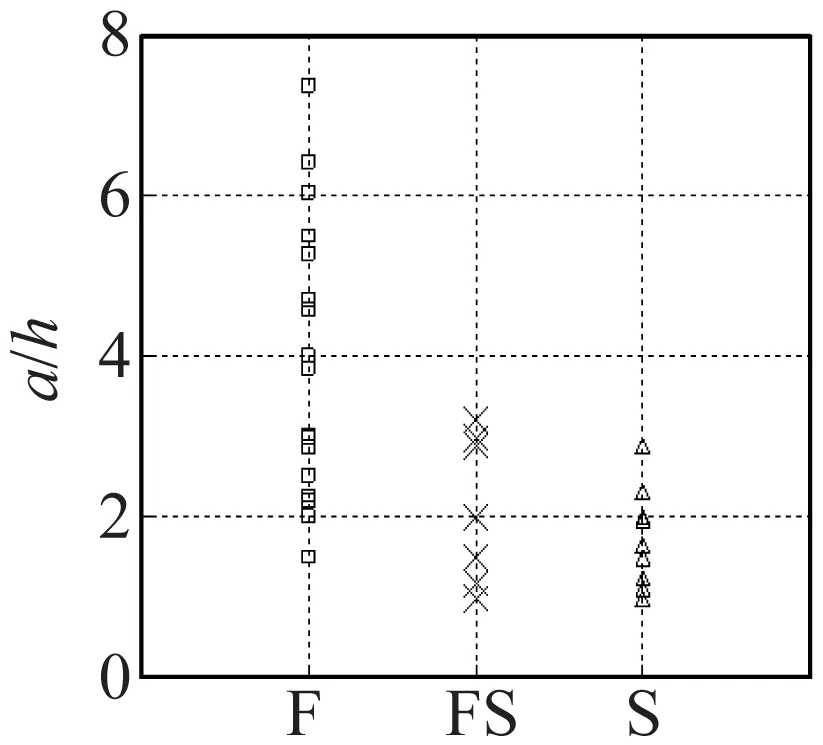
2.2.3 剪跨比
剪跨比a/h反映了构件截面所承受弯矩与剪力的相对大小,即正应力和剪应力的相对关系,是构件抗剪承载力计算的重要参数,同时影响了构件是否发生脆性剪切破坏。