电伴热布置方式对管内熔盐解冻过程的影响研究
2022-03-18王佳明曾柱楷徐顺塔
王佳明,黄 静,曾柱楷,曾 勇,徐顺塔,刘 豪
(1.中国电建集团中南勘测设计研究院有限公司,湖南 长沙 410014;2.华中科技大学煤燃烧国家重点实验室,湖北 武汉 430074)
太阳能光热发电技术因其能够耦合热能储存系统,可实现电力连续、稳定供应输出,且并网性能良好,被认为是未来替代火力发电的主要清洁供能形式[1]。在光热系统中,熔盐相较其他传热材料因具有低蒸气压力、低黏度、高热容量、较宽的运行温度范围(120~1 000 ℃)以及低成本等优势,被作为一种传热与储热工质而广泛使用[2-3]。但需要指出的是,熔盐的高凝固点特性(120~240 ℃)[4]使得熔盐在流动过程可能因热损失过大而发生凝固冻结现象。
目前,相比太阳能集热管内熔盐流动传热特性研究[5-7],管内熔盐的凝固和熔化过程研究较少。Bergan[8]利用热熔盐直接填充冷吸热器的吸热管道,发现冷充过程中吸热管道内存在局部熔盐凝固现象。Lu等[9-10]发现只有当熔盐温度高于一定程度时,热熔盐冷填充水平冷管道时才不会发生凝固现象。Pacheco等[11]和Gregory等[12]指出,对熔盐冻堵的管道进行解冻,可能会因熔盐体积膨胀将导致管道发生不可逆的塑性变形。为了实现太阳能热发电站中熔盐管道防凝,通常在熔盐管道外壁敷设矿物绝缘电缆进行伴热。Bonanos等[13]发现在电伴热带加热熔盐管道的过程中,加热带与熔盐接触时会发生损坏。廖志荣等[14]基于焓法模拟分析了管道外壁面电伴热的安装角度及功率对管内熔融盐熔化过程的影响,发现电伴热安装位置与重力方向所称的夹角不应过大,并且电伴热功率与熔盐完全熔化所需的时间呈非线性关系。
综上分析,针对电伴热熔盐管道解冻问题,当前研究重点分析了电伴热安装位置和加热功率对管内熔盐熔化过程的效率的影响,而尚未关注电伴热敷设面积大小的影响。本文利用焓-孔隙法对电伴热作用下水平管内熔盐的解冻过程进行模拟计算,并探讨电伴热根数、敷设面积和加热功率对熔盐熔化过程的均匀性和加热效率的影响,以期为熔盐管道系统中电伴热的优化设计与合理布置提供指导。
1 计算模型与工况
1.1 几何模型及边界条件
图 1(a)所示为加装电伴热的水平管道模型,其中,管道的内外径分别为50 mm和60 mm,管道的密度、比热容、导热系数分别为8 030 kg/m3、502.48 J/(kg·K)、16.27 W/(m·K)。如图1(a)所示,水平熔盐管道的外壁面加装有圆形电伴热,其安装位置与重力方向呈β角度,加装电伴热的管道外表面包裹严实的保温层。该管道内填充二元熔盐作为传热介质,其由60% NaNO3和40% KNO3组成,其热物性参数见表1。在解冻过程中,电伴热通过加热管道使其升温,进而促使管内熔盐受热熔化。考虑到熔盐熔化过程的膨胀系数(4×10-4)较小,故本文仅考虑管内熔盐径向的流动传热过程,而忽略了熔盐轴向膨胀流动。图1(b)给出了管道的二维简化模型,管道内壁采用耦合边界,电伴热被简化为管道外壁面接触的部分弧长并将其定义为恒热流边界,而将其余管道外壁面定义为绝热边界。

表1 二元熔盐的热物性参数

图1 配有电伴热的水平熔盐管道模型:(a)实物示意图;(b)计算网格
1.2 模拟方法
针对熔化和凝固问题,采用的是Voller和Prakash[15]提出的焓-孔隙率的计算方法,引入液相率来描述固-液界面的变化过程,它是指液相区域在整个蓄热单元中所占的比例,可根据热焓平衡来计算。
单位质量相变材料的热焓值为显焓与潜焓之和,即
H=h+ΔH
(1)
其中,显焓和潜焓分别为
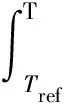
(2)
ΔH=f×L
(3)
式中H——热焓/J·kg-1;
h——显焓/J·kg-1;
ΔH——潜焓/J·kg-1;
href——参考焓/J·kg-1;
T——任意时刻熔盐温度/K;
Tref——参考温度/K;
cp——比热容/J·(kg·K)-1;
L——相变潜热/J·kg-1;
f——液相率,其表达式如下
(4)
式中Ts——凝固点/K;
Tl——结晶点/K。
控制方程如下:
(1)连续性方程
(5)
(2)动量方程
x方向
(6)
y方向
(7)
(3)能量方程
(8)
式中ρ——密度/kg·m-3;
t——时间/s;
u和v——x和y方向上的速度分量/m·s-1;
μ——动力粘度/Pa·s;
λ——导热系数/W·(m·K)-1;
P——压强;
Su和Sv——x和y方向上的动量源项;
Sh——能量源项。
动量方程和能量方程的源项
(9)
(10)
(11)
式中α——体积膨胀系数;
g——重力加速度/m·s-2;
b——用来避免分母出现零的现象取值0.001;
Amush——糊状区域常数,取105。
本文采用有限体积法离散熔盐管道二维模型的计算域,激活Solidification/Melting模型,依据布西涅斯克(Boussinesq)近似来分析相变区域的自然对流,分别采用SIMPLE和PRESTO算法求解速度和压力耦合方程和压力方程,其余方程均考虑二阶迎风格式以确保模拟计算的精度。当连续性方程相对残差小于10-3,能量方程相对残差小于10-8,其他残差小于10-6时,判定计算收敛。
为确保模拟结果的正确性,对网格数量和时间步长的独立性进行分析。结果发现,采用网格数量为2 053与采用网格数量为7 737和20 689时数值模拟获得的管内熔盐峰值温度差异较大,但采用网格数量为7 737和20 689时模拟的峰值温度较为接近,差值维持在0.2 K以内。此外,采用时间步长为0.1 s和1 s获得峰值温度模拟值的差异较小(<0.2 K)。为了节约计算成本,本文采用网格数量为7 737的管道模型,并且时间步长选用1 s。
1.3 模拟工况
表 2列出了本研究过程中电伴热的计算工况,包括3个研究变量:电伴热的根数(M)、敷设面积(以敷设圆周弧长(L)表示)和加热功率(P)。
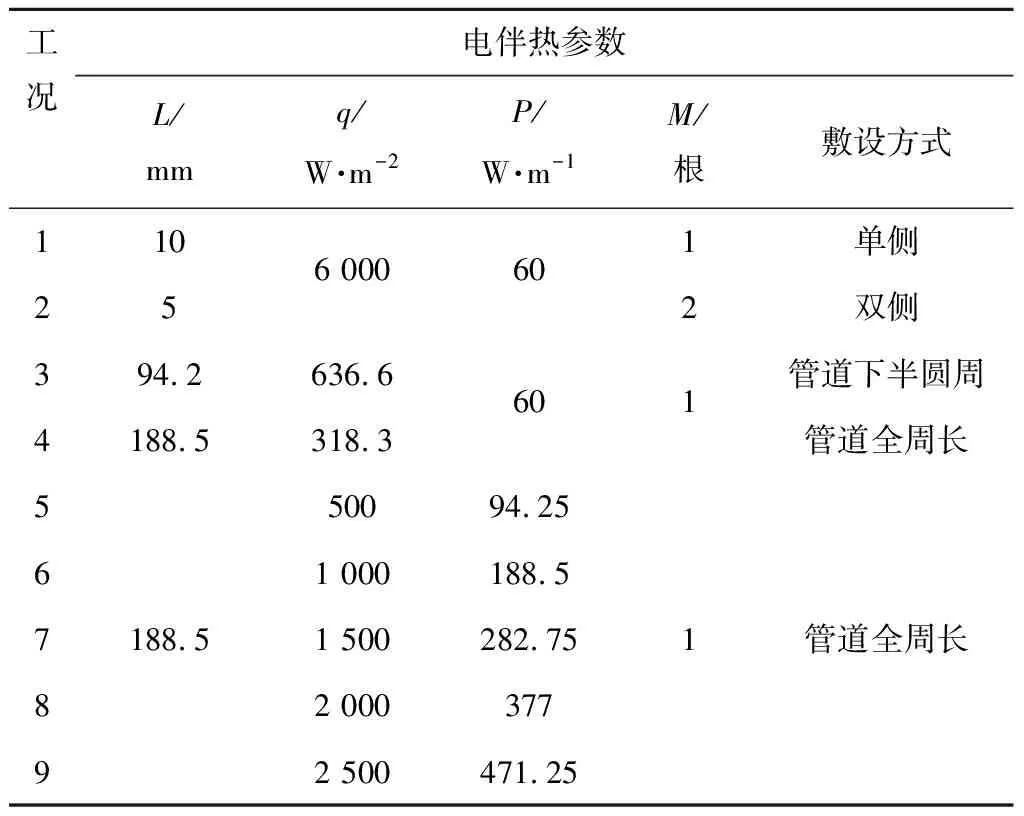
表2 电伴热运行工况
在电伴热的总L和P不变的条件下,M从1根增加到2根,即单根电伴热的L从10 mm减小到5 mm,即工况1和2,以揭示单根电伴热单侧布置加热和多根电伴热双侧布置加热方式之间的差异;进一步,在控制电伴热总功率(60 W/m)不变的条件下,电伴热的L从10 mm(局部)逐渐扩大到94.2 mm(管道下半圆周),再到188.5 mm(管道全圆周),相应地,电伴热的热流密度(q)从6 000 W/m2降低到318.3 W/m2,以揭示电伴热敷设面积对熔盐熔化过程的影响,即对比工况2~4;最后,采用管道外壁面全部敷设电伴热的加热方式(也即均匀加热)时,电伴热的P从94.25 W/m增加到471.25 W/m,即对比工况5~9,以揭示采用均匀加热的伴热方式时电伴热的加热功率对熔盐熔化过程的影响。
2 算法验证
Pacheco等[11]提供了管内熔盐凝固过程的实验研究数据,而当前研究对熔盐熔化过程的实验研究数据报道较少。考虑到熔盐的熔化和凝固过程实质上均为固-液相变过程,故可近似认为熔化和凝固相变过程是可逆过程。基于此,本文采用文献[11]中熔盐凝固过程的实验数据对当前的数值模型的有效性进行验证。
在模拟验证中,管道模型及其边界条件与实验工况[11]严格保持一致,其中,管道内外径分别为22.1 mm和25.4 mm,管道和管内熔盐的初始温度设为580 K,管道内壁与熔盐计算域相接触的界面采用耦合边界,管道外壁面采用自然对流边界且传热系数设为5 W/(m2·K)。图 2对比了管道壁面最低和最高温度值的实验和模拟结果,发现时间段的模拟和实验值呈现高度一致,说明了当前模拟方法的有效性和可靠性。

图2 熔盐自然冷却凝固过程中管道外壁温度的实验值(Pacheco[11])和模拟值的对比
3 结果与讨论
3.1 电伴热单侧和双侧敷设于管道时熔盐的解冻过程
图3给出了电伴热(β=30°)双侧布置下管内熔盐液相率(f)和流场迹线分布随时间的变化。值得一提的是,电伴热布置在β=30°位置时,熔化过程效率和均匀性更佳[14]。电伴热启动时(即加热时间t=0),管道和管内熔盐的温度均为480 K。图3(a1)所示,电伴热开始加热30 min后,靠近电伴热处的熔盐最先开始升温,固态熔盐开始熔化形成混相态,此时管内熔盐液相率的最大值(fmax)为0.22。图3(b1)给出了30 min时管内熔盐的自然对流情况,因管内不同区域熔盐存在温差导致其密度发生变化,并在重力作用下,电伴热周围先熔化的熔盐沿着内壁面向管道上方流动,此时自然对流强度较弱,最大流速仅为5×10-4mm/s。当电伴热加热到70 min时,管内固态熔盐已全部熔化,完全处于混相状态,其熔盐液相率的最小值(fmin)和最大值分别为0.023和0.63,并且液相熔盐沿管壁不断向管道顶部流动聚集,导致管内熔盐上下分布不均匀。继续加热到110 min,混相熔盐主要聚集在管道上半区域,此时管内熔盐液相率的fmin和fmax分别为0.24和0.72,两者差异相比70 min时缩小,即熔化均匀性增加。进一步加热到150 min,管内部分熔盐完全熔化形成纯液态熔盐,同时自然对流强度明显提升,最大流速达到0.43 mm/s。

图3 电伴热双侧布置时熔盐解冻过程中液相率分布(a1-a4)和自然对流(b1-b4)情况
总体而言,加热过程中,电伴热周围的熔盐最先开始升温熔化,并在自然对流的驱动下,沿着管壁向管道上方流动,并在顶端汇聚后向下流动,强化管内固-液相熔盐之间的热量传递和交换,进而加速熔盐熔化。
图4(a)所示为电伴热单侧和双侧敷设于管道外壁时管内熔盐熔化过程中温度(T)变化。熔盐的熔化过程一般经历五个区段,包括纯固态区、纯固态+混相态区、混相态区、混相态+纯液态区、纯液态区。以电伴热双侧布置工况为例,电伴热开始加热18.5 min后,管内熔盐均处于纯固相状态,熔盐的最大温度(Tmax)最先达到凝固点温度(494 K);继续加热,熔盐的Tmax不断升高并超过了494 K,管内部分熔盐开始进入混相区。加热到54.5 min,管内熔盐的最低温度(Tmin)也达到了熔盐的凝固点,此时管内熔盐已完全进入混相区;加热148 min后,管内熔盐的Tmax达到熔盐的结晶点511 K,此时管内部分熔盐完全熔化形成纯液态盐;直到170 min,管内熔盐的最低温度也上升到511 K,意味着管内熔盐全部熔化形成纯液态盐,并且继续加热,管内熔盐温度的上升速度有所加快,温差稳定维持在4 K以内。

图4 电伴热单侧和双侧敷设加热时管内熔盐解冻过程中温度和液相率的演变
当电伴热单侧布置加热时管内熔盐同样也经历相似的相变熔化过程。由图4(a)可知,不同的是,当电伴热总功率保持不变时,相比双根电伴热双侧布置加热方式,单根电伴热单侧布置加热方式下管内熔盐的Tmax更快上升到熔盐凝固点494 K,这是因为单根电伴热单侧布置加热时局部热功率更大,导致电伴热加热初期(在85 min内)管内熔盐峰值温度更高,意味着管内熔盐更早开始熔化进入混相区(如图4(b)所示)。然而,当采用双根电伴热双侧对称布置时,加热过程中管内熔盐温度的最小值始终更高,导致熔盐液相率的最低值同样也更大,最终导致熔盐完全熔化所需的时间从单侧布置加热方式下的230 min降低到双侧布置加热方式下的180 min,即电伴热总功率一定时双侧布置方式相比单侧布置方式的熔盐熔化效率更高。此外,图4(c)和(d)可以看出,电伴热双侧布置加热方式下管内熔盐温度的最大差值(ΔTmax)或液相率的最大差值(Δfmax)始终比电伴热单侧布置加热方式下要低,其中当电伴热敷设方式由单侧转变为双侧时,熔盐熔化过程中最大Δfmax从0.70减小至0.62,降低了11.4%,说明电伴热双侧布置加热方式下管内熔盐熔化过程更加均匀。因此,在熔盐管道电伴热布置设计时,应避免电伴热单侧局部集中布置,而是尽量采用多根电伴热对称布置。
3.2 电伴热敷设面积的影响
考虑到多根电伴热代替单根电伴热进行对称布置时,管内熔盐熔化过程更快速、更均匀,故在采用电伴热对称敷设方式的基础上,进一步扩大管道外壁面电伴热的敷设面积,即变化敷设的圆周弧长(L),考察电伴热敷设面积对管内熔盐熔化过程的影响。图 5所示为在保持总功率(P=60 W/m)不变条件下,电伴热的L从10 mm(工况2,局部β=30°)先增大94.2 mm(工况3,管道下半圆周)再增到188.5 mm(工况4,管道全圆周)时,熔化过程中管内熔盐液相率分布。当加热60 min时,由于L为10 mm工况下电伴热安装位置较低,故管道下方靠近电伴热处的熔盐最先开始熔化形成混相区,而电伴热敷设弧长从10 mm扩大188.5 mm(即管道全圆周)时,管道上方内壁附近的熔盐也开始熔化形成混相区,且上下分布较为均匀。加热到80 min,因自然对流强度提升,熔化的熔盐开始向管道上方流动并聚集,即使采用管道全局加热方式(L=188.5 mm),管内熔盐的液相率也开始出现上下分布不对称的现象,但相比局部敷设电伴热加热方式时管内液相率分布仍然较为均匀。总体来看,L为10 mm时,管内熔盐的熔化最不均匀,其次是L为94.2 mm,而L为188.5 mm最均匀。
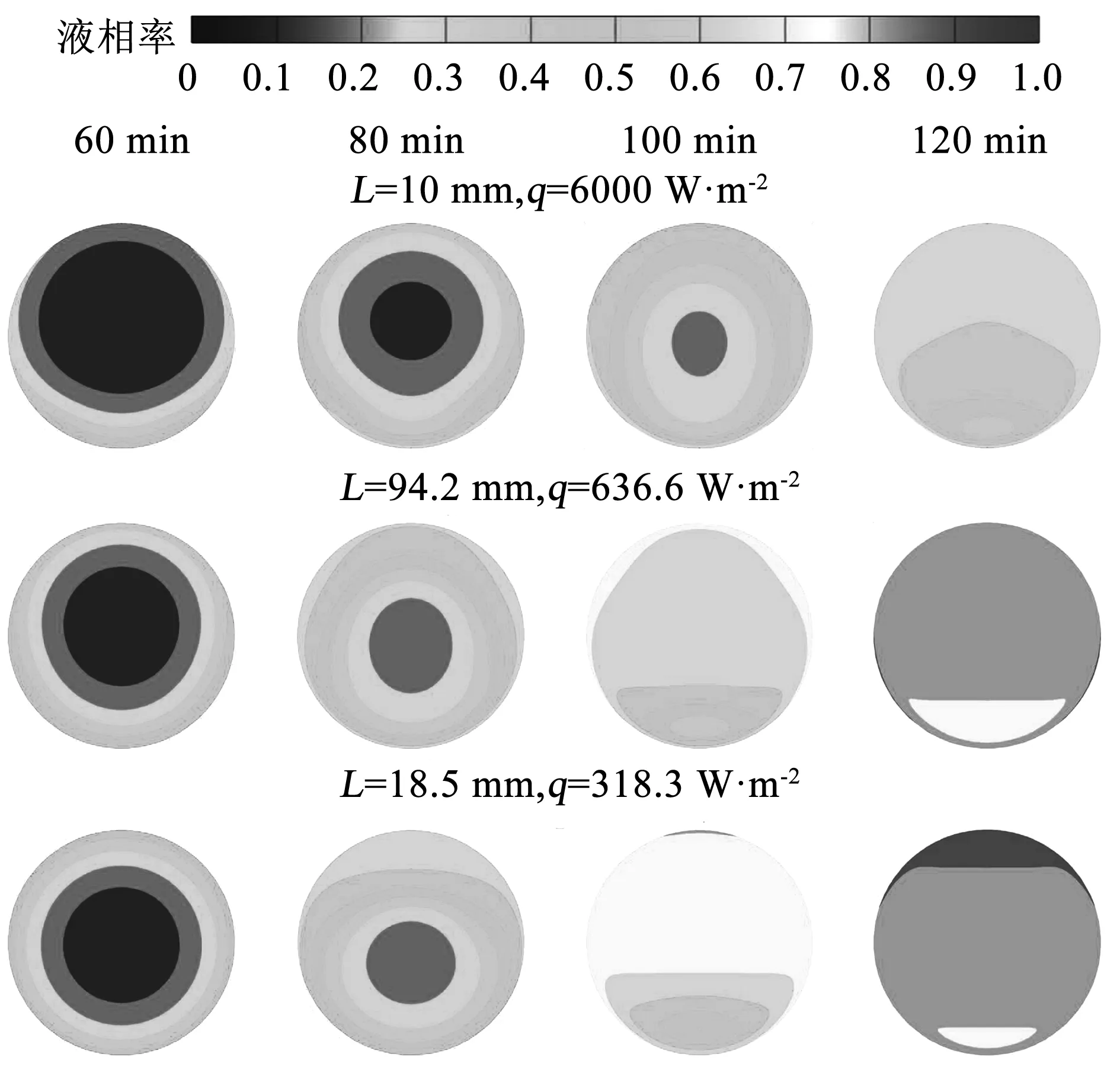
图5 变化电伴热敷设弧长时管内熔盐熔化过程中液相率的分布
图6(a)给出了当保持总功率一定条件下,不同电伴热敷设弧长下管内熔盐温度的最低值和最高值随加热时间的变化。当L为10 mm时,管内熔盐的熔化过程和L为94.2 mm和188.5 mm的熔化过程相差较大。L为10 mm时,电伴热热流密度最大,使得加热初始阶段熔盐的峰值温度最高,电伴热周围熔盐最先熔化形成混相态。不同的是,随着电伴热敷设弧长从10 mm增加到188.5 mm,同一时刻下管内熔盐的最低温度增加,导致熔盐完全熔化所需的时间从175 min减小到139 min,熔化时间缩短了20.6%,意味着熔盐完全熔化的时间效率提升。此外,由图 6(b)可知,管道外壁局部小面积敷设电伴热(即L=10 mm)时,管内熔盐温度的最大差值(ΔTmax)最大,峰值ΔTmax为11.8 K。当电伴热敷设弧长增加到94.2 mm(管道半周长),峰值ΔTmax随之减小到9.8 K,若进一步扩大电伴热敷设弧长至188.5 mm(管道全周长),则峰值ΔTmax进一步减小到9.4 K,提升了20.3%,这表明管道外壁面电伴热敷设面积增加,熔盐熔化过程的均匀性提升。因此,实际在电伴热敷设安装过程中,应尽可能扩大电伴热与管道外壁面之间的接触面积(如在电伴热上加装具有高导热性能的铜肋片等)或采用具有均匀加热特性的伴热方式(如感应加热)等以实现熔盐快速、均匀熔化。
3.3 电伴热加热功率的影响
上述分析已经证明,当管道外壁全局包裹电伴热加热(即均匀加热方式)时,管内熔盐熔化过程的均匀性最佳且熔化时间最短,故本节在采用均匀加热方式下,进一步考察电伴热功率(也即均匀加热功率)对管内熔盐熔化过程的影响。
图 7所示对比了电伴热功率从94.25 W/m增加到471.25 W/m时管内熔盐的最低温度随时间的演变过程以及完全熔化所需的时间。随着电伴热功率增加,同一时刻管内熔盐的最低温度更高,且上升速率更快,意味着大电伴热功率条件下,管内熔盐更快实现完全熔化。然而,图 7显示了电伴热功率与熔盐完全熔化时间呈现非线性关系。当电伴热功率从94.25 W/m增加到282.75 W/m时,管内熔盐完全熔化所需的时间从90 min减少到31 min,熔化时间缩短了65.6%,进一步增加功率到471.25 W/m时,熔盐完全熔化的时间缩短到20 min,仅缩短了35.5%。由此可见,在均匀受热方式下成倍增加电伴热功率无法实现成倍地降低熔盐完全熔化所需的时间,换句话说,当电伴热功率增加到一定程度后,继续提高电伴热功率对降低熔盐熔化时间的改善作用减弱。
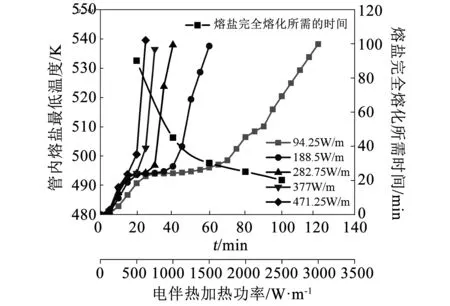
图7 管外壁在均匀伴热下变化电伴热功率时管内熔盐解冻过程中的最低温度及完全熔化所需的时间
图8所示为加热能量为339.3 kJ/m时电伴热功率从94.25 W/m增加到377 W/m工况下,管内熔盐的温度和液相率分布情况。有趣的是,随着电伴热功率从94.25 W/m增加到377 W/m,管内熔盐的最大温度从509.0 K增加到521.5 K,而最低温度却从496 K降低到493.2 K,即熔化过程中管内熔盐的温度梯度从13 K增加到28.3 K,说明大功率工况下熔化过程的温度不均匀性更大。管内熔盐的液相率随电伴热加热功率也有相似的规律。更直观地,图 8中高温区或高液相率区的面积随电伴热功率增大均扩大,同样可以说明大电伴热功率下熔化过程的均匀性更差。熔化过程中,混相态熔盐的热导率可近似认为基本不变,若要传递更高的热量,需要更大传热温差,进而导致熔化过程中的非均匀性扩大,这同时也解释了上述电伴热功率增大到一定程度继续增大对缩短熔盐熔化时间的效果减弱的现象。
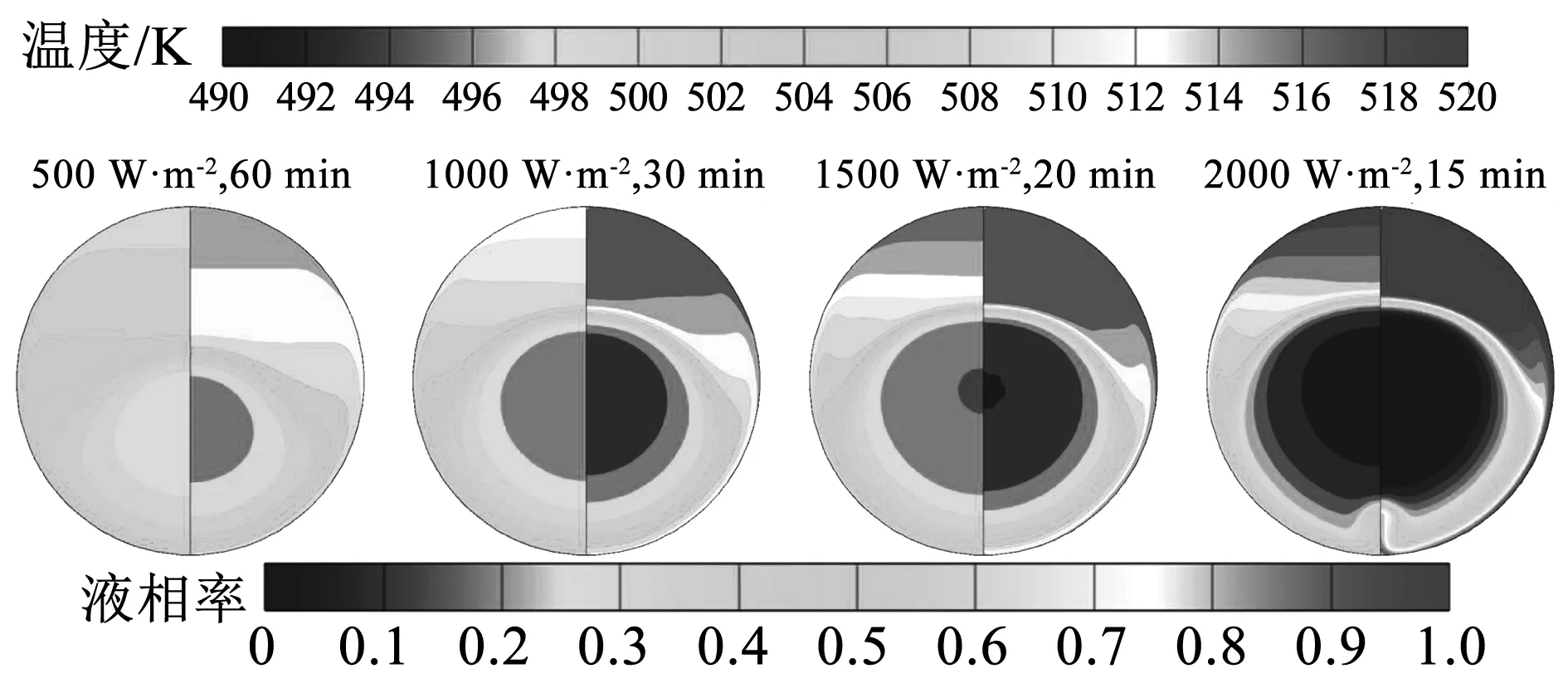
图8 管外壁均匀受热下变化热功率时管内熔盐的温度(左侧)和液相率(右侧)分布(总加热能量为339.3 kJ/m)
3 结论
本文开展了电伴热管道内二元熔盐固-液相变的解冻过程的模拟计算,对比分析了电伴热单侧和双侧布置时管内熔盐熔化过程的差异,并揭示了电伴热敷设面积和均匀伴热方式下加热功率对熔盐熔化过程的均匀性及完全熔化所需的时间的影响,得出如下主要结论:
(1)管内熔盐在靠近电伴热处最先开始熔化形成混相态,并在自然对流驱动下,先熔化的熔盐沿着管道内壁不断向管道上方流动并在顶端聚集,强化了管内熔盐之间热量传递,进而加速熔盐熔化。与单根电伴热单侧布置方式相比,双根电伴热双侧对称布置方式下管内熔盐熔化过程更均匀,熔盐完全熔化所需的时间更短。
(2)在保持总功率相同条件下,电伴热敷设的圆周弧长(即单位长度电伴热敷设的面积)从10 mm扩大到188.5 mm,管内熔盐完全熔化所需的时间从175 min减小到139 min,熔化时间缩短了20.6%,同时熔化过程的温度均匀性提升了20.3%。实际中,应尽可能扩大管道外壁面电伴热的敷设面积或采用均匀加热的伴热方式(如感应加热)来改善熔盐熔化过程的均匀性的同时提高熔化效率。
(3)当管道外壁全部敷设电伴热进行均匀加热时,加热能量为339.3 kJ/m下电伴热加热功率从94.25 W/m增加到377 W/m,熔盐完全熔化所需的时间缩短,但熔化过程中管内熔盐的温度梯度从13 K增加到28.3 K。
