特征融合与灰色回归的滚动轴承性能退化评估

杨创艳，马 军，王晓东，罗 亭，李卓睿

（1.昆明理工大学信息工程与自动化学院，云南昆明 650500；2.昆明理工大学云南省人工智能重点实验室，云南昆明 650500）

1 引言

滚动轴承是旋转机械的关键零部件之一，其运行质量决定设备运行的整体稳定性和高效安全性，这就使利用退化指标监测轴承的运行状态显得至关重要［1～3］.但因轴承的振动特性受多种因素影响，传统退化指标无法准确评估轴承退化状态［4，5］.因此，如何构建能有效反映滚动轴承运行状态的退化指标，已成为当前设备状态监测领域的研究热点之一.

近年来涌现出大量的退化指标构建方法，如：郑小霞等人［6］提出一种基于隐马尔科夫模型对数似然概率的退化指标；Xu 等人［7］利用一个滑动平均磨损退化指标来描述机械设备的退化过程；SHAO 等人［8］提出一种基于小波包能量矩熵的轴承性能退化指标.但以上单一退化指标所包含的故障信息量少且抗干扰能力差，严重影响滚动轴承性能退化评估的准确性［9］.所以，构建一个能全面反映轴承退化信息的高维特征集D是轴承退化状态评估的关键.

高维特征集D可体现不同特征间的差异互补性，但特征间可能存在重复性和冗余性［10～12］.因此，需要建立性能退化指标评价准则，有效剔除冗余特征.针对这一问题，郑近德等人［10］利用Fisher得分评价准则进行特征选择，剔除冗余特征；戴豪民等人［11］采用加权最大相关最小冗余的特征评价准则，选择有效特征；Zhu 等人［12］引入多类特征评价准则，选择信息量最大的特征.然而，合理的退化指标应具有良好的单调性（Monotonicity，Mon）、相关性（Correlation，Corr）和鲁棒性（Robust，Rob）［13，14］，应综合考虑Mon、Corr、Rob 的评价准则，选择能敏感表征轴承退化趋势的特征，构建敏感指标集F.此外，如何综合利用敏感退化指标集F的特征优势是轴承退化状态评估需要考虑的另一个核心问题.Tian 等人［15］将主成分分析（Principal Component Analysis，PCA）和K 近邻距离融合成一个退化指标；WU等人［16］通过度量PCA 的第一主元分量与其余分量之间的马氏距离形成了退化指标，但是经过PCA 分解分量不能保证相互独立；Sun 等人［17］使用KICA 非线性核函数将原始特征空间映射到核特征空间，分离得到相互独立的分量.因此，结合KICA和马氏距离融合特征，可以获得敏感退化指标KICAMD.

目前，利用敏感退化指标进行轴承退化性能评估还存在一些尚未解决的问题，如敏感退化指标存在虚假波动，且难以自适应确定SFT.轴承退化状态主要分以下阶段：正常状态，退化指标保持稳定；初始故障，退化指标开始线性增长；严重退化，退化指标开始斜率线性增长［18］.但是随着时间的推移，轴承故障点会被磨平，导致退化指标存在虚假波动［19］.因此，修复特征的虚假波动对于轴承性能退化的准确评估至关重要［20～23］.近年来许多研究者在此方面进行了研究，如：Ahmad 等人［19］提出了一种线性回归技术处理退化指标的虚假波动；高彩霞等人［20］使用最小二乘法确定线性回归方程来修复虚假波动；Li 等人［23］利用指数模型修复退化指标的虚假波动.但上述方法无法实现轴承退化指标的在线监测，因此，本文提出了基于灰色回归模型（Grey-regression Model，GM）修复的虚假波动.此外，确定轴承SFT，可提高性能退化评估的准确性.确定SFT 的方法有：利用工程标准ISO-10816 的μ+3σ方法［21］，以及通过大量机器统计［22］.但是，这些方法计算结果误差较大.因此，准确确定SFT 及定量评估轴承的退化阶段也直接关系到轴承运行状态评估的有效性.

综上所述，本文主要工作在于提出了一种特征融合与灰色回归的滚动轴承性能退化评估方法.本文通过构建敏感退化指标，克服了传统方法依靠经验评估轴承退化状态的局限性；同时使用GM 修复退化指标的虚假波动，基于时间序列转折突变点自适应确定SFT，提高了对轴承退化性能的评估能力；最后，通过美国国家航空航天局（National Aeronautics and Space Administration，NASA）和西安交通大学-长兴昇阳科技有限公司（Xi’an Jiaotong University-Changxing Sumyoung Technology，XJTU-SY）的滚动轴承全寿命周期数据库的数据验证了所提方法的准确性和有效性.

2 构建敏感退化指标

2.1 特征提取

2.1.1 时域统计特征

选择文献［16，17］设计的有量纲特征和无量纲特征来表征轴承振动信号xi（N为采样点）的变化趋势.有量纲特征包括均值（MV）、方差值（VARV）、均方根值（RMSV）、偏度值（SKV）；无量纲特征包括峭度因子（KF）、脉冲因子（PF）、形状因子（SF）、裕度因子（MF）.特征计算方程如表1所示.

表1 时域统计特征

2.1.2 能量特征

轴承发生故障时，故障频率范围内的信号发生变化，从而引起能量的变化.因此，引入能量E表征振动信号的冲击性故障.计算公式为

2.1.3 熵特征

为反映故障深层次的信息，通过有效度量熵值大小来提取轴承故障状态的本质信息.因此，选用几种常见熵，计算公式为

Shannon熵：

Renyi熵：

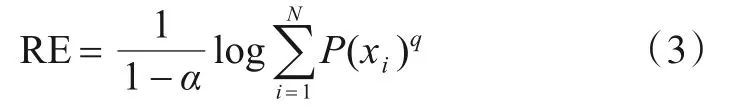
Tsallis熵：

其中，P(xi)代表轴承随机退化事件xi的概率.

2.2 特征选择

为了选择高维特征集D中的有效退化特征，需要建立相关退化特征的评价准则.一个优良的退化指标应该满足下列条件［16］：

（1）单调性（Mon），退化是一个不可逆的单调过程；

（2）相关性（Corr），特征与时间顺序具有良好的相关性；

（3）鲁棒性（Rob），对随机噪声具有良好的抗干扰性.

因此，基于Mon、Corr、Rob的综合评价准则，来选择合理的退化特征，具体步骤如下.

Step1对高维特征集D中的特征使用平滑法分解为平滑趋势项和随机项，即

其中，f(tk)是tk时刻的特征值；fT(tk)是趋势项；fR(tk)是随机项.

Step2计算特征的Mon、Corr、Rob，即

其中，δ(·)是单位脉冲函数.

Step3使用熵值法确定加权线性组合系数ωi，得到综合评价指标Z，即

Z和信号正相关，值越大说明该特征越应该保留.保留大于阈值A（取Z的均值）［15］的特征，构建敏感指标集F；否则予以剔除.

2.3 特征融合

为了综合F中所有特征的优点，利用KICA 把输入空间中的数据映射到特征空间，然后在特征空间中进行分析和处理，具体步骤如下.

Step1输入数据集x=(x1,x2,…,xn)和核函数kij=(xi,xj),其中i,j=1,2,…,n（n为数据样本）.

Step2构造核矩阵K=k-Ink-kIn+InkIn，其中In为单位矩阵.

Step3数据集x白化处理，Χ=-1HTK，其中Λ为核矩阵K最大特征值，H为Λ对应的特征向量.

Step4采用ICA 算法得到正交分离矩阵Α和独立元T：T=ΑTΧ.

Step5计算第一独立元与其余独立元之间的马氏距离，并选取其中最大值作为最佳投影向量，最终得到敏感指标KICAMD，即

其中，μ和S-1分别是独立成分的均值和协方差.

3 回归修复虚假波动及状态定量评估

在KICAMD 的基础上，还需解决以下问题：①判定KICAMD是否存在虚假波动并修复；②基于退化指标确定SFT和定量评估轴承的退化状态.

3.1 灰色回归模型

GM 是由一个单变量的一阶微分方程所构成，其建立过程如下：对原始数据X={x(t),t=0,1,2,···,n}平滑处理，得到X={x0(t),t=0,1,2,···,n}，然后对x一阶累加得X={x1(t),t=0,1,2,···,n}.

回归方程为

方程的解为

离散化形式为

还原数据，得到GM，即

3.2 修复虚假波动

在轴承性能退化评估中，若出现如图1所示的虚假波动，将严重影响退化指标对轴承退化状态的刻画，降低轴承性能退化评估的准确性［19～21］.

图1 退化指标虚假波动

因此，若存在虚假波动，需要修复才能作为后续评估的退化指标，具体步骤如下.

Step1基于敏感退化指标KICAMD建立滑动窗（n=50，滑动步长LS=1）［20］.

Step2在滑动窗上建立GM 得到预测值，同时，以滑动窗内数据的3δ原则设置阈值B.

Step3判断预测值是否大于阈值B.若大于则判定为虚假波动，并用预测值替代原始值；反之则用式（13）所示的相对指标KICAMDr替代.

Step4更新滑动窗，进而得到退化指标HI，即

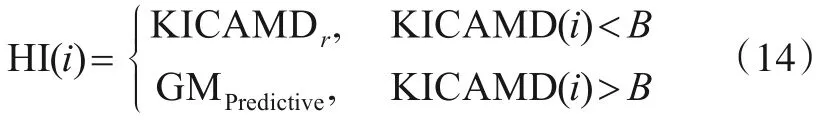
3.3 确定SFT及退化状态定量评估

引入T 分布随机邻接嵌入（T-Distributed Stochastic Neighbor Embedding，T-SNE）的高维数据可视化方法呈现轴承全寿命周期数据的全局退化趋势.该方法实现了高维特征集D到（X，Y）两个方向的特征的约简［24，25］，如图2所示.

图2 T-SNE分布散点图

根据图2 可将滚动轴承运行状态分为6 个阶段，但不能直接确定SFT 和各状态变化的起止点［25］.为此，引入时间序列突变点检测算法计算状态突变点［26］.对给定时间序列x=(x1,x2,…,xn)，按式（15）计算突变点k值［27，28］，即

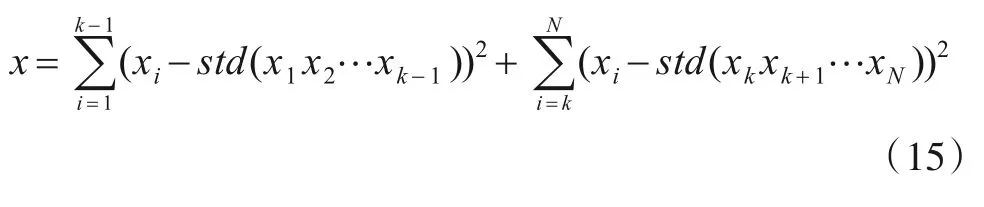
4 特征融合与灰色回归的滚动轴承性能退化评估过程

所提方法实现流程如图3所示，具体包括如下三大过程.

图3 方法实现流程

（1）构建敏感指标集

step1构建高维特征集D=［MV，VARV，RMSV，SKV，KF，PF，SF，MF，E，SE，RE，TE］.

step2计算高维特征集D中每个特征的评价指标：Mon、Corr、Rob.

step3计算加权综合评价准则Z及筛选阈值A.

step4若Z大于A则作为有效特征，构建敏感指标集F；否则，剔除该特征.

（2）修复虚假波动

step1使用KICA 对敏感指标集F进行映射处理获得最佳投影向量，建立敏感退化指标KICAMD.

step2基于KICAMD 建立滑动窗（n=50，LS=1），在滑动窗上建立GM 模型，得到预测值；同时，以滑动窗内数据的3δ原则设置阈值B.

step3若预测值大于阈值B则判定为虚假波动，用预测值取代原始值；否则，取相对指标ICAMDr.

step4更新滑动窗，得到修复虚假波动后的退化指标HI.

（3）确定SFT和退化状态定量评估

step1计算敏感退化曲线的转折突变点.

step2最初的转折突变点即为SFT.若退化指标曲线处于SFT 前，数据处于正常状态；否则，处于退化阶段.

step3以SFT 为起点，基于退化时间序列的转折突变点完成轴承的运行状态的定量评估.

5 实验结果分析

5.1 NASA数据实验分析

实验数据采用IMS 中心轴承试验平台［26～28］，如图4所示.轴承转速为2000 r/min，采样频率为20 kHz，采样点数为20480，采样时间间隔为10 min，共采集到984组样本.图5是其全寿命周期数据时域波形.

图4 全寿命周期数据实验平台

图5 全寿命周期数据时域波形图

从图5仅能看到趋势的变化，无法清楚划分轴承实时运行状态.为此，根据所提方法构建高维特征集D，并绘制其归一化特征图，如图6所示.

图6 归一化高维特征集

从图6可看出，不同特征从不同维度表征轴承的运行状态.进一步计算各特征的Mon、Corr和Rob值，如图7所示.计算综合评价指标Z，并按升序排序，选择Z≥A（A取Z的均值为0.1092）的8 个有效特征构建敏感指标集F=［VARV，RMSV，TE，SE，RE，E，MF，SF］，如图8所示.

图7 退化特征Mon、Corr和Rob

图8 有效退化特征选择

为了综合敏感指标集F中的8 个特征的优势，首先，分别使用PCA 和KICA 对高维特征集D（样本数为984 的8 维特征集）进行映射处理，分别得到得分矩阵S和转换矩阵T（样本数为984的8维矩阵）；然后，分别计算得分矩阵S和转换矩阵T的第一分量与其余分量之间的马氏距离，从而将984×8 的矩阵投影为高维空间984×984 的重构矩阵；最后，选择每个样本空间的最大值（样本数为984的1维向量）作为能全面反映轴承退化趋势的退化指标PCAMD和KICAMD.并利用K-medoids聚类方法将综合敏感指标集F融合为退化指标K-medoids［29］，如图9所示.

图9 敏感退化指标变化趋势

从图9不能直观看出3个融合指标之间的差别.因此，分别计算3个融合指标与原始信号的信噪比和相关系数，如图10 所示.从 图10 可看出，KICAMD 相 比PCAMD 和K-medoids 信噪比分别提高了75.27% 和62.83%，相关系数分别增加了57.75%和43.58%，表明了KICAMD退化指标的有效性.

图10 融合指标性能对比

但将KICAMD 退化阶段进行局部放大（图11）发现，其也存在明显虚假波动.为此，分别引入线性回归［19］、指数回归［23］和GM 方法对其进行修复，得到修复后的退化指标HI，如图11中红色曲线所示.

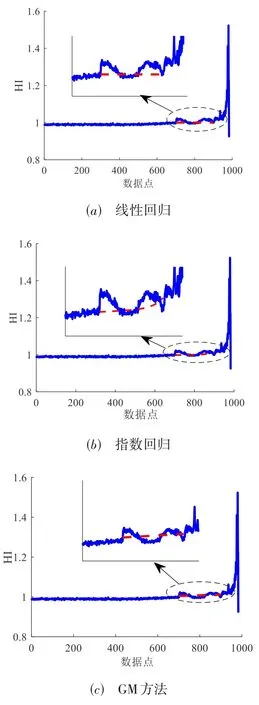
图11 退化特征虚假波动修复

进一步计算HI 和KICAMD 的均方根误差（RMSE）和相关系数，如表2 所示.对比表2 可知，GM 方法的RMSE最小，相关系数最大，论证了GM方法的有效性.

表2 HI和KICAMD的RMSE和相关系数

为定量评估轴承的退化状态，将完全失效时间（第984 组）作为为终止故障时间（End Failure Time，EFT），进而计算得到HI 时间序列的5 个转折突变点（532.5，699.5，800.5，900.5，965.5），如图12所示.

从图12 可看出，5 个转折突变点将HI 分为呈梯度上升的6 个状态.由于转折突变点在第532.5 组（非整数），为确定SFT 的取值，获取第532 组和第533 组的Teager 能量算子解调频谱图，如图13 所示.从图13 可知，仅在第533 组的频谱中发现与轴承外圈故障频率234.4Hz 相近的频率，且存在明显的2～4 倍频，由此确定SFT=533.

图12 时间序列突变点监测

图13 Teager能量算子解调谱

确定SFT 后，根据HI 的转折突变点绘制滚动轴承性能退化阶段（后续状态点均选择了转折突变点前一组数据），如图14所示.从图14可清楚观察到轴承退化的阶段过程：正常状态［1，533）；早期故障［533，699）；轻微衰退［699，800）；衰退增长［800，900）；严重衰退［900，965）；失效状态［965，984］.

图14 轴承性能退化阶段

为验证所提方法的有效性，表3 对比了HI 及修复虚假波动后单一退化指标的初始退化时间.从表3 可以看出，HI 的初始退化时间更早出现，结合图13 也充分说明了其合理性.

表3 性能退化指标SFT对比

5.2 XJTU-SY轴承数据实验验证

实验所用的轴承加速退化测试平台XJTU-SY 的平台图如图15所示［30，31］.其采样频率为25.6 kHz，采样间隔1 min，每次采样时长为1.28 s，转速为2400 r/min，外圈理论故障频率为123.36 Hz.

图15 加速退化测试平台

图16 是其外圈全寿命周期数据时域波形.从图16不能直接观察到2410 组之前是否发生故障.为此，构建高维特征集D，并基于Mon、Corr、Rob 评价准则得到综合评价指标Z，如图17 所示.Z按升序排序后选择了Z≥A（A=0.1082）的6 个有效特征，构建敏感特征集F=［SE，VARV，RMSV，RE，E，MF］，如图18所示.

图16 全寿命周期数据时域波形图

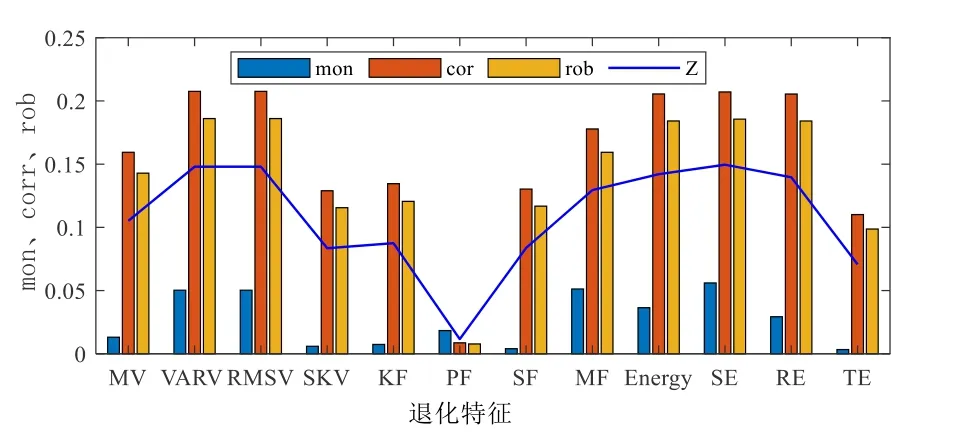
图17 退化特征的Mon、Corr和Rob

图18 有效退化特征选择

采用与5.1 节相同的实现过程，获得了经GM 修复后的退化指标HI，如图19 所示.进一步计算得到退化指标HI 时间序列的4 个转折突变点（2344，2392，2464，2511），如图20 所示.同时，为验证SFT 的准确性，呈现了如图21 所示的第2344 组的Teager 能量算子解调频谱.从图21 的频谱可知轴承发生外圈故障.因此，选择SFT=2344是合理的.

图19 GM虚假波动修复

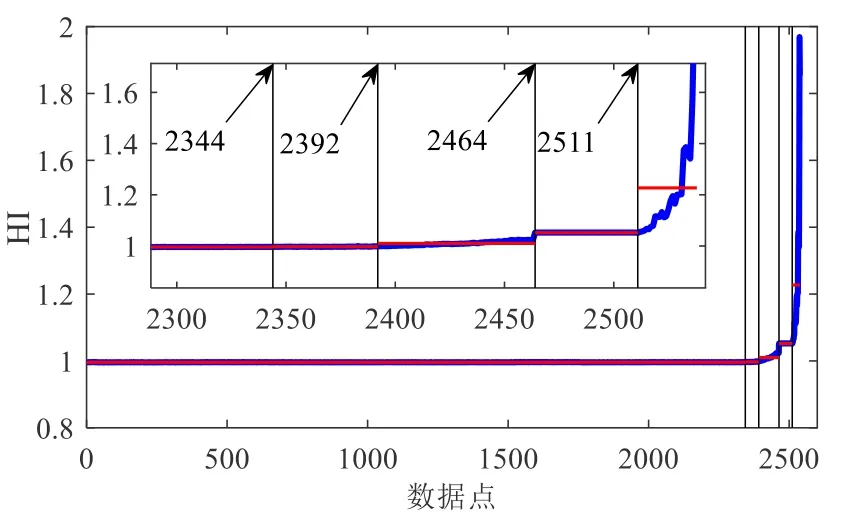
图20 时间序列突变点

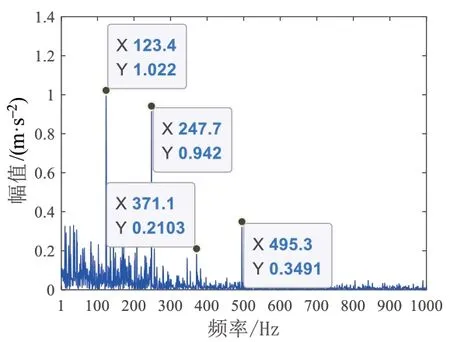
图21 第2344组Teager能量算子解调谱

在图20 中，4 个转折突变点将HI 分为呈梯度上升的5 个状态，对应轴承的5 个退化过程（图22）：正常阶段［1，2344）；早期故障［2344，2392）；轻微衰退［2392，2464）；衰退增长［2464，2511）；失效状态［2511，2538］.

图22 性能退化阶段

6 结论

针对传统退化指标无法准确反映滚动轴承全寿命周期内退化状态的问题，引入KICA 和马氏距离融合多退化指标，提出了一种特征融合与灰色回归的滚动轴承性能退化评估方法，并通过实验验证了所提方法的准确性和有效性，具体总结如下：

（1）基于Mon、Corr、Rob 的综合评价准则选择有效退化特征，构建了有效且全面地表征轴承性能退化状态的敏感指标集，为性能退化的准确评估奠定基础；

（2）利用GM 方法修复退化指标的虚假波动，提高了滚动轴承状态定量评估的可靠性；

（3）自适应确定退化指标HI的时间序列的突变点，实现了滚动轴承性能退化定量评估，克服了传统初始故障时刻的确认方法依靠经验和实验观察的主观性和局限性.

所提方法可以准确且有效地评估轴承的退化过程，但进一步讨论退化趋势失效阈值自适应判定方法，将更利于实现滚动轴承在线评估和制定更有针对性的维护策略.