不同混杂结构下广义倾向性评分法的模拟研究及应用*

山西医科大学卫生统计教研室(030001) 王晨晨 孙 倩 王 彤

【提 要】 目的 通过构建存在不同混杂结构的广义倾向性评分(generalized propensity score，GPS)模型和结局模型，探索比较三种GPS估计法：广义倾向性评分-最小二乘法(generalized propensity score-ordinary least squares，GPS-OLS)，广义倾向性评分-增强算法(generalized propensity score-boosting，GPS-Boosting)以及协变量均衡广义倾向性评分(covariate balancing generalized propensity score，CBGPS)法对混杂因素的均衡性能及对暴露效应估计的影响，并将其应用于连续型自变量与健康结局的关联性研究。方法 通过蒙特卡洛模拟，分别生成不同样本量的样本(N=400与N=1000)，利用GPS-OLS、GPS-Boosting以及CBGPS方法模拟4种不同混杂结构存在的暴露因素模型和结局模型，按照逆概率加权法构造相应的权重，并依据各协变量与暴露因素相关系数变化情况来估计三种GPS估计法均衡混杂变量的能力，通过对比偏倚和均方误差的大小来反映其对暴露效应估计的影响。将其应用于2017年山西省营养调查研究，探讨肉类食物摄入量和高血压之间的关联性。结果 在4种混杂结构存在的情况下，相比于GPS-OLS法和GPS-Boosting法，CBGPS法均衡混杂因素的能力最佳。在暴露效应估计方面，CBGPS法也能明显降低暴露效应估计的均方误差以及偏倚程度，估计效果优于GPS-OLS法、GPS-Boosting法。结论 使用广义倾向性评分均衡混杂因素时，优选CBGPS方法。同时使用GPS法在实例中验证了肉类食物摄入量和高血压之间的关联性。

倾向性评分法(propensity score，PS)是观察性研究中均衡已观测混杂效应的有力工具，可以解决多个协变量在暴露组与处理组之间的分布不均衡的问题。PS得分指给定一些观察到的变量，估计出的观察对象能够划分入暴露组的条件概率[1]。近年来有大量学者研究各种PS的估计方法以及均衡性诊断[2-3]。在PS得分估计中，应用最广泛的有logistic回归、判别分析、协变量均衡倾向性评分(covariate balancing propensity score，CBPS)、机器学习等。传统的PS模型主要针对二分类暴露因素的混杂效应[4]，然而在很多实际观察研究中，研究者感兴趣的暴露因素是连续型变量而不是二分类变量，例如具有公共卫生干预意义的BMI等，此时针对二分类暴露因素的PS估计法、混杂效应诊断等就不再适合。通过设置阈值把连续型变量转换为二分类的情况并不少见，有研究者在检查青少年吸食大麻对成年早期吸食大麻的影响时对大麻吸食量进行了二分法，而实际上大麻吸食存在(并且确实被报告)为一个连续的范围，从不食用到经常食用[5]。如果在实际研究中把像BMI这样的连续型变量人为地二分类化之后再构建PS模型，会导致偏倚发生和误导性的推论[6]。相对于二分类暴露因素的PS估计法，用于连续型暴露因素的广义倾向性评分(generalized propensity score，GPS)的估计和对应的均衡性能的诊断都是比较复杂的[7]。2012年Flores等研究者[8]提出采用广义线性模型通过最小二乘估计法估算GPS(generalized propensity score-OLS，GPS-OLS)。2015年Zhu等学者[9]给出了关于Boosting的广义倾向性评分估计法(generalized propensity score-boosting，GPS-Boosting)计算GPS，这种方法使用逆概率加权法构造权重，然后基于边际结构模型估计暴露效应，并采用相关系数代替标化均值差等指标诊断GPS估计法的均衡性能。Fong 等学者[10]在2018年基于CBPS提出了协变量均衡广义倾向性评分(the covariate balancing generalized propensity score，CBGPS)法计算GPS，并指出这种方法在非线性情况下依然能够很好地消除混杂因素的影响。如果GPS模型和结局模型带有一些复杂结构形式，利用上面的三类方法均衡混杂因素的能力和其对暴露效应估计的影响目前尚不清楚。

本研究旨在通过构建存在不同混杂结构的GPS模型和结局模型，探索比较三种GPS估计法：GPS-OLS，GPS-Boosting以及CBGPS法对均衡混杂因素的性能及对估计暴露效应的影响。进一步把GPS方法应用到公共卫生领域，探讨肉类食物摄入量和高血压之间的关联性。

GPS估计法原理

如果T表示连续型暴露因素，X表示基线变量，Yi(t)，t∈ψ表示观察单位i接受T=t暴露因素的结局，ψ表示暴露因素所有可能的取值，那么当T表示二分类变量时，ψ={0，1}，当T为连续型变量时，ψ∈R。若μ(t)=E[Yi(t)]，表示接受某水平暴露因素T=t之后，观察对象出现结局的平均水平。广义倾向性评分GPS=r(t，x)表示在一些协变量X的基础上，暴露因素T的条件概率密度函数r(t，x)=fT|X(t|x)，也就是GPS=fT|X(t|x)。

GPS-OLS、GPS-Boosting以及CBGPS三种方法估计出GPS得分之后，使用逆概率加权法构造权重，基于边际结构模型，最后通过加权回归估计暴露效应。一般来说当暴露因素为二分类变量时的权重W(T)[11]表示为：

若将此权重应用于连续型变量，那么当一些观察的因素T与协变量X相关性很大时，会引起r(t，x)的变化很大，可能权重会出现极值，最终导致W(T)的分布不满足渐近正态性[12]。因此，针对这种连续型暴露变量T对应的权重W(T)可表示为：

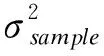
在观察到的协变量的情况下，不考虑未测量混杂因素的影响，根据倾向性评分的强可忽略假设[13]，暴露因素(T)和潜在结局(Y(0)，Y(1))之间相互独立，即Y(t)⊥T|X，t∈ψ；正向性假设，指在每一个x值上，接受处理的概率均为正数，即每个观察对r(t，x)>0，t∈T。

GPS均衡混杂效应的性能同PS一样，应用GPS之后，各协变量与暴露因素之间彼此独立，消除了混杂效应，表示为X⊥1{T=t}|r(t，X)。

1.GPS-OLS法

GPS-OLS法构造暴露因素与协变量的广义线性模型，将暴露因素T对应条件函数概率密度函数fT|X(t|X)当成是GPS，采用最小二乘法估算回归模型中的参数α和σ2，若暴露因素T与协变量X之间存在线性关系，则回归模型中的残差服从零均值、同方差的正态分布。因此：

Ti=α0+α1xi1+α2xi2+…+αjxij+εi，

εi∈N(0，σ2)

σ表示回归模型中残差的标准差，αTX表示暴露因素的平均值，因此可以用公式表示为

2.GPS-Boosting法

GPS-Boosting法为了避免主观选择变量导致的偏倚，采用非参数的方法选择协变量。这种方法主要通过增加迭代次数将弱学习器转换成为强学习器，进而获得均衡性能最佳的评分值。其中m(X)表示基于协变量的暴露因素的平均值。M表示总的回归树，当协变量X与暴露因素T之间的相关系数绝对值均值达到最小时停止迭代，此时得到的评分值均衡混杂因素的效果最佳。

T=m(X)+ε，ε∈N(0，σ2)

3.CBGPS法

CBGPS法通过矩估计代替最小二乘估计估算模型参数，主要思想是应用GPS通过逆概率加权法构造权重后，弱化协变量X*与暴露因素T*之间的相关性，从而能够模拟随机化以此消除混杂效应，由此得到的是不存在偏倚的估计值。表示为：

模拟研究

1.模拟研究设置

本研究使用R 3.5.1软件进行模拟研究。建立从简单的模拟场景到比较复杂的结构，模拟过程中首先生成连续型的结局变量Y，连续型暴露因素T以及10个协变量X，均服从一种均值为0、方差为1、协方差为0.2的多元正态分布，变量之间对应的关系形式见图1。

图1中协变量X2、X4以及X5与暴露因素T和结局因素Y均有关，协变量X1和X3只与暴露因素T有关，与结局因素Y无关，而协变量X6只与结局因素有关，与暴露因素无关。在实际研究中，研究者往往会观测许多变量，但其中大多数变量往往与T或Y并不相关，分析中均衡所有的变量不是很现实。本模拟研究中GPS模型或结局模型中并不包含所有变量，如(X7，X8，X9，X10)。其中场景1中的GPS模型与结局模型均为简单线性情况，在其他场景中为了增强混杂结构的复杂性，通过不断增加协变量反映暴露因素、结局和协变量之间的可能存在的关系，探索3种GPS估计法均衡混杂因素的情况以及对暴露效应估计的影响。

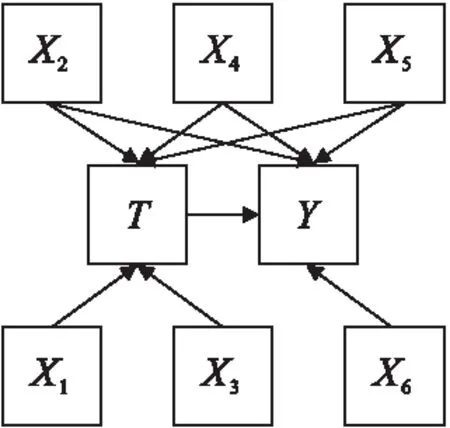
图1 变量间关系图

模拟场景设置情况如下：

场景1：广义倾向性评分模型与结局模型均设置为简单线性情况。

T1=X1+X2+0.2X3+0.2X4+0.2X5+ξ1

Y1=X2+0.1X4+0.1X5+0.1X6+T1+ε1

ξ1是服从N(0，4)的误差项，ε1是服从N(0，25)的误差项。

场景2：广义倾向性评分模型设置为非线性的情况，也就是模型错误设定的情况；而结局模型还是场景1中的简单线性情况。

T1=0.4X1+(X2+0.5)2+0.4X3+0.4X4+0.4X5+ξ2

Y1=X2+0.1X4+0.1X5+0.1X6+T1+ε1

ξ2是服从N(0，2.25)的误差项。

场景3：广义倾向性评分模型设置为简单线性情况，是模型的正确设定的情况；而结局模型设置为非线性的情况。

T1=X1+X2+0.2X3+0.2X4+0.2X5+ξ1

Y1=2(X2+0.5)2+0.5X4+0.5X5+0.5X6+T1+ε1

场景4：广义倾向性评分模型设置为非线性的情况，也就是模型错误设定的情况；而结局模型设置为非线性的情况。

T1=0.4X1+(X2+0.5)2+0.4X3+0.4X4+0.4X5+ξ2

Y1=2(X2+0.5)2+0.5X4+0.5X5+0.5X6+T1+ε1

本研究依据4种组合，分别生成样本量N=400的小样本与N=1000的大样本两种情况，应用GPS-OLS、GPS-Boosting、CBGPS三种估计法估计GPS，通过逆概率加权构造权重，在加权后样本中诊断均衡性能。平均相关系数r为10个协变量与暴露因素之间的相关系数绝对值的均值，用于诊断几种估计方法均衡性能。因为实际中无法直接准确地判别暴露因素、协变量与研究结局之间的联系，所以一般模拟时都是将协变量线性纳入模型，重复模拟1000次。

本研究关注的是三种GPS估计方式对混杂因素的均衡效果和对暴露效应估计的影响。诊断均衡性能时采用相关系数来判定，则相关系数小于0.1时认为该方法均衡混杂的性能比较好[14]；若在0.1～0.3的范围内，那么该方法效果一般。相关系数表示为：

判断估计暴露效应的评价标准一般利用偏倚(bias)还有均方误差(MSE)。分别表示为：

2.模拟研究结果

(1)样本量为400时的模拟结果

表1结果显示，应用几种GPS估计法加权后的平均相关系数相对于原始样本的平均相关系数均有降低。其中，CBGPS法均衡混杂效应的能力最好，其次是GPS-OLS法，最后是GPS-Boosting法。CBGPS法在4种场景中的平均相关系数均<0.1，并且相对于其他GPS估计法均衡混杂的性能都更加稳定。GPS-Boosting法与GPS-OLS法均衡混杂效应的能力有些差距，GPS-Boosting法平均相关系数>0.3，可以认为在这个方法均衡混杂效应的能力一般。

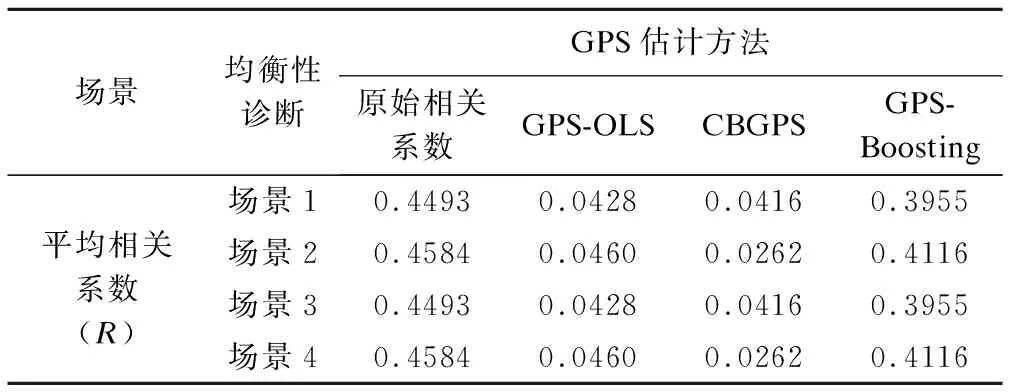
表1 三种GPS估计法混杂效应均衡能力比较(N=400)

表2显示了三种GPS估计法对暴露效应估计的影响。可以发现，在三种GPS估计法中，CBGPS法能明显降低暴露效应的估计偏倚，暴露效应估计精度最高。其次，GPS-OLS法相对于传统逐步回归法，偏倚与均方误差均有一定程度的降低，GPS-Boosting法暴露效应的估计偏倚和均方误差稍稍提升。综合均衡混杂因素能力及估计偏倚与精度上来看，GPS-OLS法略微优于GPS-Boosting法，但最佳的GPS估计仍然是CBGPS法。其次，在场景4中，即当广义倾向性评分模型设置为非线性的情况，也就是模型错误设定的情况，而结局模型设置为非线性的情况时，所有方法产生的偏倚都是最大的。当结局是线性时，即在场景1和场景2中，CBGPS法都能够得到很好的估计，且GPS-OLS法仅次于CBGPS法。

表2 三种GPS估计法对暴露效应估计精度影响比较(N=400)

(2)样本量为1000时的模拟结果

当样本量N=1000时，采用GPS-OLS、GPS-Boosting、CBGPS三种估计法得到的均衡混杂能力以及暴露效应估计的比较结果类似小样本的情况，详见表3和表4，此不赘述。

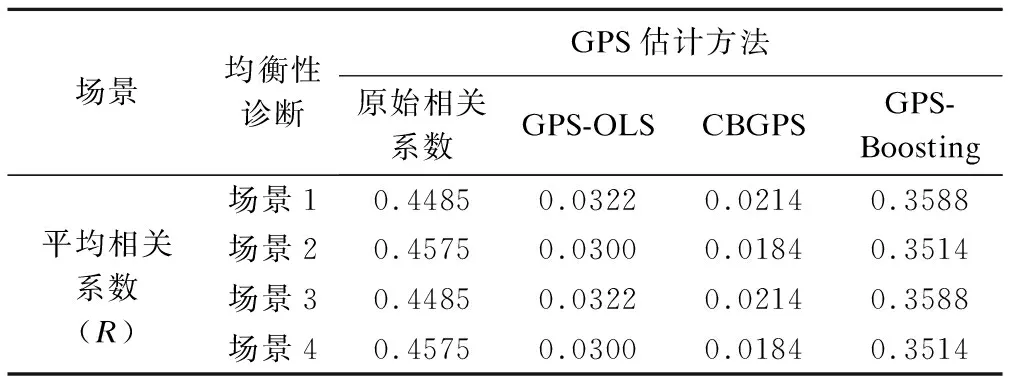
表3 三种GPS估计法混杂效应均衡能力比较(N=1000)

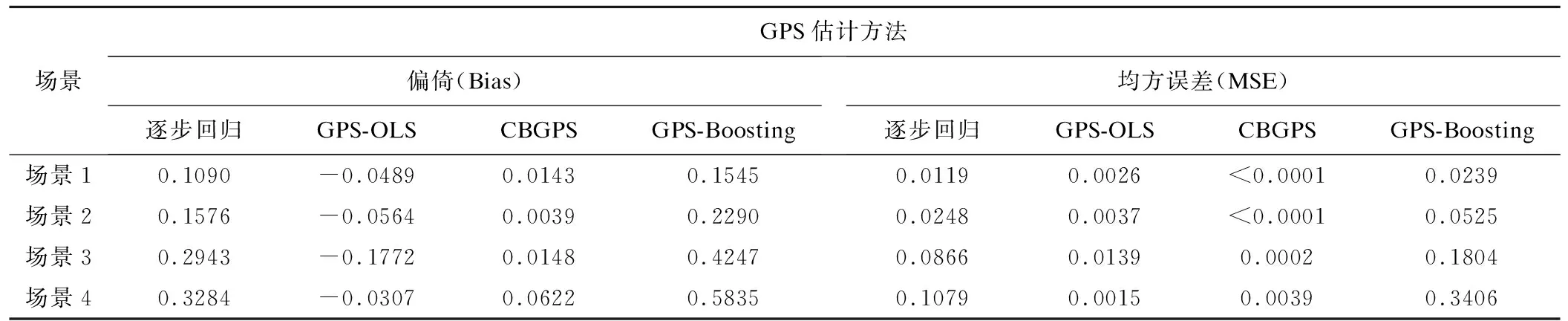
表4 三种GPS估计法对暴露效应估计精度影响比较(N=1000)

实例分析

1.研究对象

2017年在山西省开展了一项人群慢性病及其危险因素的横断面调查，在省内每个检测点对18岁以上居民进行了抽样，对研究对象进行一般人口学、生活习惯、体力活动与膳食问卷等调查，同时检测其血压等指标。排除信息缺失或出现极端值以及素食主义者，共纳入5649人。本研究以肉类食物摄入量和高血压之间的关联作为实例验证，比较三种方法对估计暴露效应的影响。

2.统计方法

使用SAS 9.4软件以及R 3.5.1软件进行统计分析，P<0.05认为具有统计学意义。基线的定量资料统计描述采用均值和标准差，组间比较采用t检验；定性资料统计描述采用频数和百分比，组间比较采用χ2检验。然后通过GPS-OLS、GPS-Boosting以及CBGPS法分别估算GPS，逆概率加权法构造权重，经过加权回归研究肉类食物摄入量与高血压之间的关联。

3.分析结果

(1)基本情况

由表5得出，BMI、性别以及饮酒、受教育的程度以及婚姻情况等都和高血压有一定的关联，在日常饮食中，大米、杂粮、油炸面食、加工肉、内脏、水产、坚果以及甜食的摄入与高血压有关，见表6。

表5 基线变量统计描述

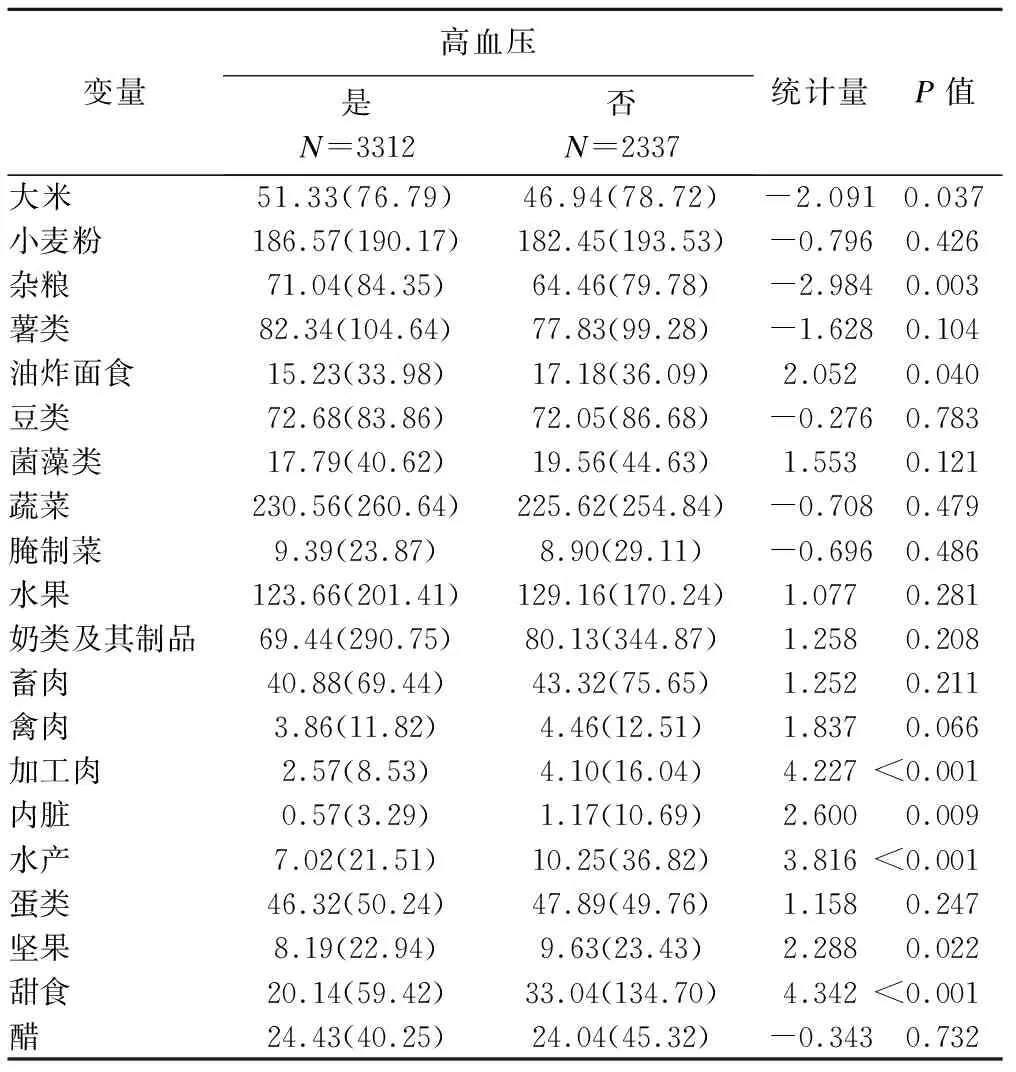
表6 基线变量统计描述

(2)模型拟合

使用各个基线协变量与肉类食物摄入量进行模型拟合，因变量为肉类食物摄入量，性别、BMI等基线协变量纳入GPS模型。如表7结果显示，与肉类食物摄入量相关系数最高的是蔬菜类，其次是甜食、加工肉以及牛奶摄入量。

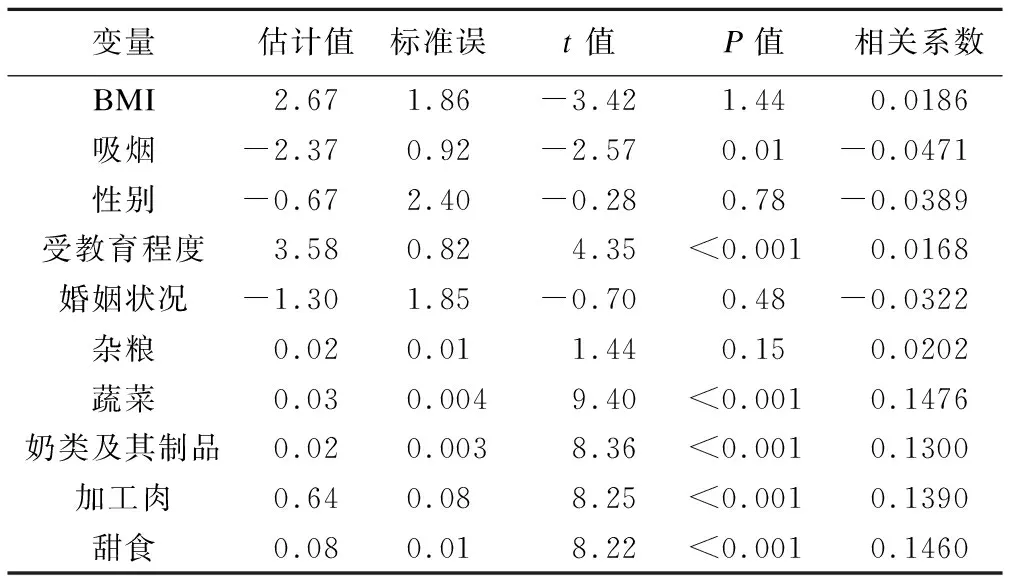
表7 肉类食物摄入量与基线协变量进行模型拟合

根据相关系数的变化情况诊断三种GPS估计法的均衡效果，比较出三种方法的优劣。表8的结果显示，各个基线协变量与肉类食物摄入量的原始相关系数均值为0.0580，其中蔬菜类(r=0.1476)、甜食(r=0.1460)、加工肉(r=0.1390)、奶类及其制品的摄取数量(r=0.1300)和加工肉的摄入量相关性比较强。在均衡混杂因素后，GPS-OLS法的相关系数为0.0166，GPS-Boosting法的相关系数均数为0.0286，CBGPS法的相关系数均值均接近为0，表明三种方法中CBGPS法均衡性能比较好。由图2可见在三种估计方法中，CBGPS法均衡混杂的性能最佳，GPS-Boosting法最差。

表8 三种GPS估计法拟合后的相关系数变化

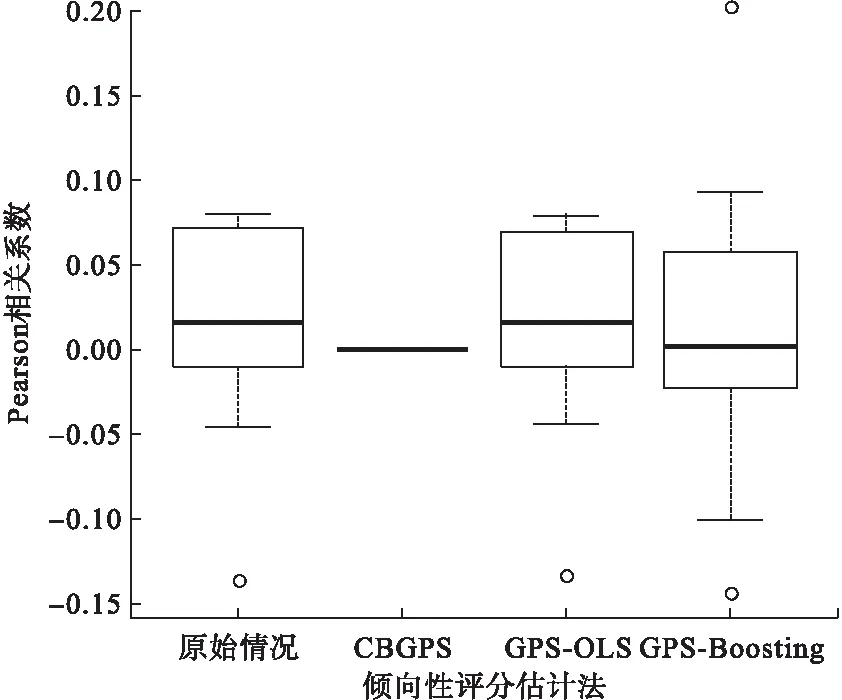
图2 相关系数箱式图

表9多因素分析结果显示，多因素分析与三种GPS模型纳入的自变量一致，都为年龄、性别、受教育程度等因素，在进行对应的调整以后，使用传统多因素分析，得到肉类食物摄入量与高血压之间的关联无统计学意义(OR=1.0002，95%CI：-0.0006～0.0012)。分别应用这三种方法后，可以得出日常膳食中肉类食物摄入量的增加与高血压患病有关，其中应用CBGPS法(OR=1.0002，95%CI：0.0001～0.0004)均衡效果最佳，参数置信区间最窄。

表9 肉类食物摄入量与高血压之间的多因素分析

讨 论

近年来，PS的应用已经越来越广泛[15]。Austin[16]对比了CBGPS法、GPS-OLS法，采用回归均衡混杂因素的影响，结果显示两种GPS估计方法都有较好的均衡混杂效果。本研究通过模拟研究和实例验证相结合，系统地比较了GPS-OLS法、GPS-Boosting法、CBGPS三种广义倾向性评分估计法均衡混杂因素的能力以及对暴露效应估计的影响。较之于GPS-OLS法、GPS-Boosting法，CBGPS法均衡混杂因素效果最佳。在暴露效应估计方面，CBGPS法也能明显降低效应估计的均方误差以及偏倚程度，估计精度明显优于GPS-OLS法、GPS-Boosting法。故本研究建议当暴露因素属于连续型变量时，可以优先选择CBGPS法均衡混杂因素。

在暴露为连续型变量的情形下，有研究者在结局变量也是连续型变量时应用GPS法均衡混杂因素[17]。如Keisuke Hirano等[18]探索了奖金金额对劳动者收入的影响；Zhang等[19]研究了母亲的孕前体重指数对婴儿出生体重的影响；Imai等[20]分析了吸烟量的增加对医疗费用造成的影响。本研究给出了结局变量为是否患高血压的二分类情形下的应用。

实例研究结果显示，通过使用传统逐步回归法调整各个混杂因素，如性别、年龄等因素，肉类食物摄入量与高血压之间的关联并没有统计学意义(OR=1.0002，95%CI：-0.0006～0.0012)。但考虑到这种方法可能会引入估计偏倚[21]，采用GPS方法进行校正。通过应用CBGPS法后，得出日常饮食中增加肉类食物摄入量可能会引起患高血压的风险升高(OR=1.0002，95%CI：0.0001～0.0004)。此外，通过GPS-OLS法(OR=1.0005，95%CI：0.0002～0.0007)和GPS-Boosting法(OR=1.0148，95%CI：0.0095～0.0198)也能够得出肉类食物摄入量的增加可能引起患高血压的风险升高。本实例分析结果与以往研究结果一致[22]，有许多研究也表明肉类食物摄入量与高血压有统计学关联。尽管利用GPS方法均衡混杂因素之后，肉类食物摄入量与高血压之间的关联有统计学意义，但是从图2可以看出，利用GPS-OLS法与GPS-Boosting法，加权前后各协变量与肉类食物摄入量之间的相关系数变化不大，均衡混杂因素效果均不如CBGPS法；而采用CBGPS法之后，各协变量与肉类食物摄入量之间的相关系数基本接近于零值，混杂效应均衡效果较好(表8)。

由于实例调查研究中所涉及的变量较多，无法将所有变量全部纳入，并默认没有纳入的协变量与肉类食物摄入量、高血压无关，以此来满足模型假设，可能存在潜在偏倚。尽管本研究发现了CBGPS法均衡效能较好，但也有研究表示[20]，若GPS模型出现了错误指定的情况，那么CBGPS法就会变得不灵活；本次模拟研究设置的混杂结构只有4种，还不够全面，现实情况的混杂结构可能更为复杂；此外本研究中只研究了低度非线性的情况，如GPS模型或结局模型中只存在一个协变量交互项或只有一个二次项的情况，而现实情况中可能出现更多的高阶项或交互项，而本研究模拟中并未考虑，仍有待后期探索。本研究考虑了应用逆概率加权法进行混杂因素的均衡策略，但有研究表明当存在强混杂效应时，加权法相比回归调整法在效应估计精度上有更大的变异[16]，所以在均衡混杂效应的策略上还有待探索。