几类奇数阶幻方构造的程序实现

李建华，许芝卉

（山西大同大学数学与统计学院，山西大同 037009）

幻方是个古老的数字游戏，历史悠久。它不仅在数学中占有一定的地位，而且在计算机科学中也有广泛的应用。n阶幻方是指一个从1到的自然数组成的方阵，其每行、每列以及两对角线上元素之和相等。目前，关于奇数阶幻方构造的方法已相当丰富。

1 传统连续摆数法

在文献[1]中，作者给出了2n+1 阶幻方构造的传统构造方法，其构造步骤为：

Step1：将1 放到第一行的中间；

Step2：其它2-（2n+1）×（2n+1）的数字依次放在前一个数字的上一行后一列的空格中。如果到达最上一行，则把数字放在最后一行后一列的方格中；如果到达最右端，则把数字放在第一列的上一行的方格中；按这个方法找到的位置已填有数字，则将此数放在前一个数的正下方的方格中。

用C程序实现如下：

2 先纵后横错位摆数构造法

在文献[2]中，给出了根据幻方的定义及其性质利用先纵后横错位构造的方法对2n+1 阶幻方的构造[2]，其构造步骤为：

Step1：将（2n+1）×（2n+1）个数字放入2n+1 阶矩阵中，从1 开始，依次存放，按先行后列的顺序存放；

Step2：先进行列变换，从每一列起依次变换（中间列不参与变换），依次将本列移出上面的数字推接到此列的下面，第一列移一个数字，第二列依次移两个数字，依此类推；

Step3：然后进行行变换。每一行（中间行不参与变换）依次往前推数字，前面推出去的数字接到后面。第一行推移一个数字，第二行推移两个数字，依此类推。

用C程序实现如下：

运行结果如图1-4所示。

图1 3阶幻方

图2 5阶幻方

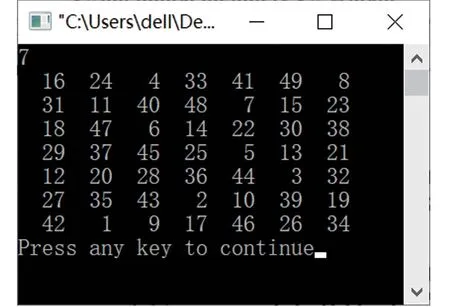
图3 7阶幻方

图4 11阶幻方

3 基于传统摆数法的一种改进法

文献[3]中提出了一种改进的连续摆数法。这种方法的第一个数可以在任意位置，而且可以按人为的意愿选择下一个数的位置，但其它数字都得遵循这个规律[3]。具体步骤如下。

step1：以奇数阶幻方中心位置为坐标原点，建立坐标系；

step2：将幻方中任意一格的位置用坐标来表示，坐标范围从

step3：定义“起始向量”，表示1 的位置；

step4：定义“偏移向量”，表示一个数的位置到下一个数位置所指的方向，依次按顺序填写其它数字;

step5：当遇到要填入的格子中已经被其它数字占据，用“中断向量”重新计算该数字的坐标，当得到的坐标超出范围，用“模n加”的方法计算新的合理的坐标，并将该数字填入坐标所对应的位置；

step6：重复step 4 和step 5，直到所有数字入方格中。

这种填法需要特别注意：

中心数之前的数不能放入中心位置。一但中心数之前的数通过这种方法被放入中心位置，那么这个起始向量，或是偏移向量的选取不合适，必须进行调整更换；

用C程序实现如下：

运行结果如图5-7：

图5 初始坐标(0,-1)，偏移量(2,1)的5阶幻方

图6 初始坐标(2,-2)，偏移量(3,1)的7阶幻方

图7 初始坐标(3,4)，偏移量(1,-2)的九9阶幻方

4 结语

幻方作为一种“思维体操”，可以培养人们学习数学的兴趣，开发智力，拓宽思路[4-5]。用C 程序来实现幻方的构造，更有助于培养程序设计的逻辑思想。