COX回归模型的贝叶斯分析

苗新利

（楚雄师范学院数学与计算计科学学院，云南楚雄 675000）

1 概述

生存分析过程中,在利用可能存在删失数据的生存资料拟合COX 比例常数回归模型[1]时，首要的前提是基于生存数据拟合的COX 模型满足风险比例是常数的假设,即PH 基准检验[1]。检验PH 假定的方法包括图示法和假设检验法，文中用的是Kaplan-Meier生存率曲线法和时依变量法。接下来是分别利用极大似然估计和贝叶斯估计[2]方法去拟合COX 回归模型，极大似然估计是属于传统频率派的范畴，而贝叶斯参数估计属于新兴的贝叶斯统计范畴，它能够更有效的利用样本信息,尤其是对小样本更有效。

1.1 COX比例风险回归模型

COX比例风险回归模型表达式是

式中,h(t)是风险函数，h0(t)是基准风险函数,β1x1+β2x2+…+βpxp是预后指数PI,其值的大小关系到生存风险的大小以及预后效果的好坏。

1.2 模型假定及检验

PH假定,即比例风险常数假定,其含义是对于任意两组数据,有

从此式可以看出,对于协变量xj,判断其是否是危险因素,关键是看变量xj前面的系数,若系数是正的,则xj是危险因素；若系数为负，则变量会降低风险；若系数为零,说明xj不发挥作用。也就是说，某影响因素是否是危险因素,取决于该因素前面系数符号的正负。

1.3 参数估计及假设检验

参数估计利用的是频率学派的极大似然估计,似然函数是

式中,分子部分代表某时刻点的风险,分母部分代表该时刻点以后所有个体的风险之和.所以上式又称为偏似然函数,利用该函数所求的极大似然估计即偏似然估计[1]。

而COX 模型的贝叶斯估计[2]利用的是马尔科夫链迭代法,又称蒙特卡罗方法。该方法利用马氏链的收敛性及相关假设检验，当相关参数的马氏链迭代到一定程度达到收敛接近稳定时，由每条链得到的参数估计的均值作为该参数的贝叶斯后验估计[3]。

2 实例分析

2.1 问题与数据结构

数据集来源于某心脏移植跟踪与研究调查案例[4],数据有65 例生存资料,其中事件发生数41 例,右删失数24 例，删失率达36.92%。接下来考察生存资料是否满足PH 假定，在上述假定成立的条件下利用极大似然估计和贝叶斯方法拟合COX 回归模型来分析各协变量对患者生存时间的影响并进行预测.本案例数据结构及分组情况见表1。

表1 心脏移植数据结构

2.2 PH假定检验

通过SAS创建名为HeartData_65 的数据集，将定量变量分组，以生存时间Time为横轴，以生存概率为纵轴，绘制7 个协变量的Kaplan-Meier生存率曲线，见图1，以变量X3(PriorSurg)的Kaplan-Meier生存率曲线为例,从生存率曲线图可以看出基本无交叉,满足PH 假定，其他6 个变量的生存率曲线图也基本无交叉，生存率曲线图在这里省略。为进一步检验7 个变量是否满足PH 假定,采用时协变量法跟K-M法进行交叉验证,检验结果见表2,由表2中结果可以看出P值均大于0.05,因此7个变量均满足PH假定。

表2 时协变量检验结果

图1 变量X3(PriorSurg)的K-M生存率曲线

2.3 极大似然估计与贝叶斯估计

在前面分析的基础上,分别利用极大似然估计与贝叶斯估计拟合COX 回归模型,拟合结果见表3,由表3中的结果可以看出,极大似然估计下的参数估计结果与贝叶斯参数估计结果回归系数符号一致,且偏差不大.风险较大的危险因素是X2(AgeAcc接受移植手术时的年龄),其次是X7(MismatchScor不匹配分数),最后是X1(TimeAcc等待移植手术的时间),其余变量是保护因素。由表3 可知，极大似然估计下的COX 回归模型是h(t)=h0(t)exp(0.125 15X1+0.964 42X2-0.810 94X3-0.763 3X4-0.854 21X5-0.430 43X6+0.665 83X7),由风险最大的危险因素X2(AgeAcc)可知,接受移植手术的年龄每增加一岁,增加的风险是2.62(e0.96442)。

表3 COX回归模型的极大似然估计与贝叶斯估计

在贝叶斯后验估计中,若参数的马尔科夫链接 近平稳，说明马氏链基本收敛。这里以变量X1(Time-Acc)的马尔科夫链诊断图为例，见图2 所示,变量X1(TimeAcc)的马尔科夫链在0.98附近做上下波动,且基本平稳,说明该链收敛,马氏链的自相关系数在2 阶之后很快收敛为零,且该变量的后验概率密度函数为正态分布,综上,可以判断该变量的马尔科夫链收敛,所以生存时间的COX贝叶斯生存模型可以表示成

图2 X1(TimeAcc)的马尔科夫链收敛性诊断图

根据表3 中7 个协变量的最高后验概率密度置信区间,保留有统计学意义的影响因素,删掉统计学意义不大的影响因素,最终的贝叶斯COX回归模型是

式中,0.9771X2-0.7787X4是预后指数PI。变量X2(AgeAcc)的系数为正,所以是危险因素,其统计学意义是接受移植手术的年龄每增加一岁,增加的风险是2.66(e0.9771)。变量X4(TransTime)的系数为负,是保护因素,术后时间超过30 d 的患者生存风险可降低45.9%，与极大似然估计下的COX 回归模型中对应变量的参数估计(0.964 42,-0.763 3)较为接近。

接下来,分别利用极大似然估计和贝叶斯估计分别拟合生存时间在不同参数模型下的回归模型,并通过比较和分析,选出较优模型。结果见表4 和表5,由表4结果可以看出五种参数分布模型下AIC 和BIC最小的均是Gamma分布，其次是Lognormal分布，由表5 可以看出DIC[5]最小的仍然是Gamma分布，其次是Lognormal分布，但由贝叶斯方法下Gamma分布的参数估计的马氏链收敛诊断图来看,其效果并没有Lognormal分布下的参数估计的收敛效果理想。

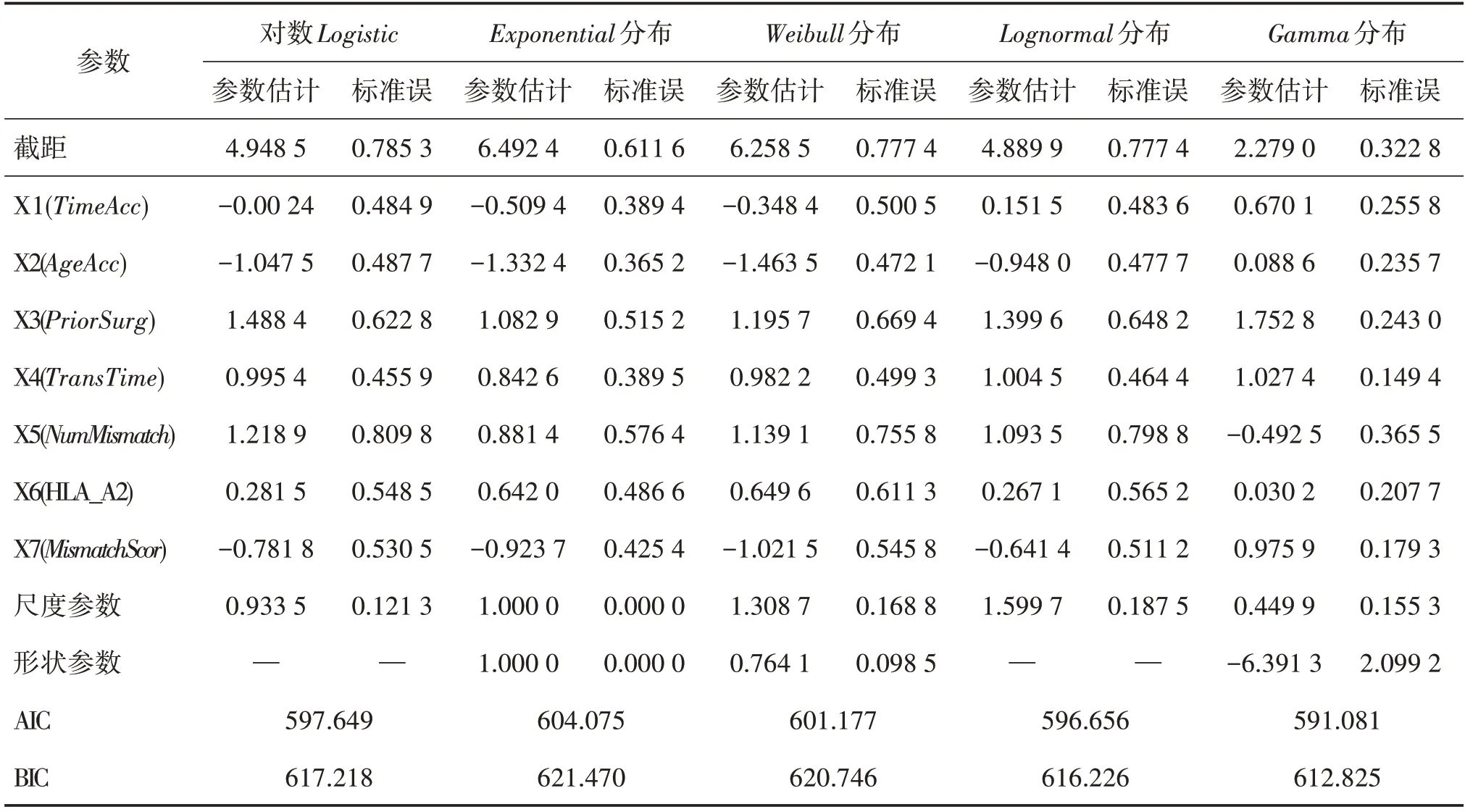
表4 五种参数模型下的极大似然估计

表5 五种参数模型下的贝叶斯参数估计

还以变量X2(AgeAcc)为例,见图3所示,图A是Gamma分布下变量X2(AgeAcc)的马氏链及相关诊断图,图C是是该分布的尺度参数马氏链及收敛性相关诊断图,图B 是Lognormal分布下变量X2(AgeAcc)的马氏链及相关诊断图,图D是是该分布的尺度参数马氏链及收敛性相关诊断图,由诊断图很明显看出,Lognormal分布下变量X2(AgeAcc)的马尔科夫链更稳定,马氏链的自相关系数在2 阶后全部为零,但Gamma分布下的参数估计马氏链收敛性较差,且该分布下尺度参数的马氏链自相关系数收敛到零的的速度较慢。综上分析，选择Lognormal分布作为生存时间t(Time)较优的参数拟合模型,且由Scale=1.8543 知,生存时间是一个右偏的Lognormal分布[6]，这和生存时间的核密度图所呈现的趋势一致，见图4。极大似然估计下的Lognormal分布模型是

图3 X2(AgeAcc)马尔科夫链收敛诊断图

图4 生存时间t的核密度图

其中

变量t是生存时间。

贝叶斯参数估计下的Lognormal分布模型是

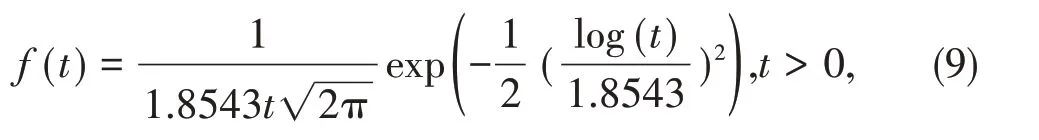
其中

3 结语

基于生存资料分别利用极大似然估计和贝叶斯参数估计两种不同方法分别拟合了生存时间的不同参数回归模型和半参数回归模型，并对模型进行了简单的分析和预测。通过拟合COX比例风险回归模型,发现两种方法下的参数估计值偏差并不大,且贝叶斯参数估计方法能够更多的利用样本信息,由贝叶斯参数估计下的COX回归模型得出危险因素是接受心脏移植手术的年龄，保护因素是接受手术的时间.为了进一步比较极大似然估计和贝叶斯后验估计,对生存时间分别在五种不同参数分布下利用这两种方法进行拟合,由于贝叶斯参数估计方法能够更有效地整合样本信息和先验信息,对样本容量大小无特别要求,拟合下来,通过比较与分析,最终选定对数正态分布作为生存时间的后验分布,这与生存时间的分布趋势基本一致。通过以上分析，贝叶斯参数估计相较于极大似然估计，方法上更高效，能够突破大样本的限制，结果更直观，更有说服力，所得结果对心脏移植手术会有一定的参考作用。