跳频通信系统仿真设计与性能分析
2022-03-17汤巧治陈双燕
汤巧治,陈双燕
(闽南理工学院工业自动化控制技术与信息处理福建省高校重点实验室,福建石狮 362700)
跳频通信是扩频通信的一种,具有较强的抗干扰能力,在抗干扰、移动通信、微波等领域都有广泛的应用[1]。在对跳频通信基本原理进行阐述的基础上,采用Matlab/Simulink 对跳频通信系统进行了仿真,并分析了系统各点处信号的频谱,重点对不同跳频速度下系统的误码率进行了分析。
1 跳频通信系统原理分析
跳频通信系统框如图1所示[2]。跳频系统是一种用随机码序列进行多元频移键控(M-FSK)的通信方式,即通信中使用的载波频率受伪随机变化码的控制而随机跳变。根据跳频速率Rh和信息传输速率Ra的关系,将跳频系统分为慢跳频与快跳频:当Rh>Ra时是快跳频,当Rh<Ra时则是慢跳频[3]。发送端按不同跳频指令去控制频率合成器,发射机输出频率在宽范围内随机改变,使射频载波也在宽范围内变化;为了对输入信号进行解扩(即解跳),需要有与发端相同的跳频指令去控制频率合成器,使其输出的跳频信号在混频器中,能与接收到的跳频信号差频出一个固定中频信号;经中频放大器后,送到解调器恢复出原基带数据信号信息[2]。
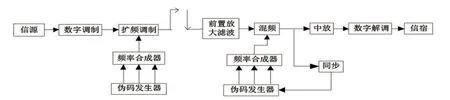
图1 跳频通信系统框图
由于跳频系统中载频不断改变,在接收机中跟踪载波相位较为困难,所以跳频系统中一般采用非相干调制方式,最常见的是FSK 调制[3]。设数据流波形为a(t),数据速率为Ra,其取值为双极性(±1),进行FSK 调制(频偏Δf)后输出信号的等效低通信号为b(t)[3],有:

设伪随机序列控制下的瞬时频率为f(t),随着时间改变,f(t)取值的频率点fi,i=1,2,…,N上改变。跳频载波信号的等效低通信号c(t)设为:

跳频就是以跳频载波对数字调制信号进行频谱搬移的过程,因此跳频输出的等效低通信号d(t)为:
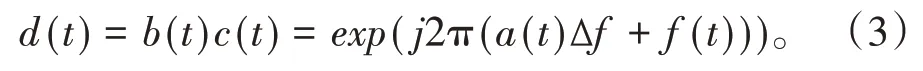
接收端,以同步PN 码控制的频率随机变化的本地载波(其等效低通信号为发送载波c(t)的共轭信号c*(t)和接收信号混频(相乘)进行解跳,所得解扩输出信号[3]为:

其中,n(t)和J(t)分别表示,背景(高斯)噪声和干扰(单频)信号。(3)式第一项即为解跳后的窄带信号;第二项为扩频后的宽带噪声以及干扰信号,此项再经窄带滤波器即可滤除,达到抗干扰目的[3]。
2 跳频系统仿真设计
基于Matlab/Simulink 对跳频通信系统进行建模,跳频点数N=64,Rh=50 跳/s,具体模型如图2所示[3]。

图2 跳频通信系统Simulink模型
选用Bernoulli Binary Generator 模块作为二进制数字信源来产生单极性非归零矩形脉冲(NRZ),采样时间设置为0.01 s,因此二进制信源输出数据速率(下称数据率)为100 bit/s。本跳频系统模型的跳频点数固定为N=64 个,跳频的频率间隔固定为50 Hz,因此扩频后的频谱带宽为50 × 64=3200 Hz。为了便于观察,设置系统频谱观测范围为-2 000~2 000 Hz,Simulink 仿真环境的采样率为4 000 次/s,信源数据率为100 bit/s,因此每个二进制符号采样点数为40 点。采用M-FSK Modulator Baseband 模块完成2FSK 调制,调制元数为2 个,频率间隔150 Hz。主要研究跳频速度对系统性能的影响,图2 中跳频速度为Rh=50跳/s,即每跳持续时间为0.02 s。2FSK 调制模块中,每个二进制符号的采样点数N2FSK=4000 × 0.02=80点,最终2FSK 输出的是采样率为4 000 次/s 的复信号。
用于产生随机载波频率的随机整数子系统由Subsystem PN Sequence 产生,如图3 所示。子系统中:PN Sequence Generator 的生成多项式由模块默认生成,采样时间TPN=1/300 s,并设置成按帧输出,每帧6 个随机样值(即6 个随机码片);将帧格式转换为基于采样的信号后,用Bit to IntegerConverter 将每6 个码片转换为一个0~63 的随机整数输出,作为跳频载波频率点的控制信号。随机整数的输出速率为300/6=50 个/s。扩频调制器采用M-FSK Modulator Baseband 模块用来实现跳频扩频,其参数设置为调制元数为64,输入数据类型为整型,频率间隔为50 Hz,每个符号的采样点数N扩频=80 点,模块输出也是采样率为4 000 次/秒的伪随机跳频载波复信号,跳频点数N=64,Rh=50 次/s。该信号与2FSK 基带调制输出信号相乘以实现扩频调制。

图3 随机整数生成子系统
扩频输出信号经过AWGN 信道,并且加入了一个200 Hz 的单频正弦波作为干扰源。接收端,本地跳频载波是发送端跳频载波信号经Math Function 模块取共轭得到的共轭信号,其与接收的扩频信号相乘以完成解跳,后再经2FSK完成信息解调。
3 跳频系统仿真与结果测试
3.1 仿真环境说明
本次设计在Matlab 2014 版的仿真环境中进行,系统仿真参数按默认设置即可。AWGN 信道的噪声方差Var=2 W;单频正弦干扰信号的幅度为1 V。
3.2 跳频系统测试结果
(1)功能分析
Matlab仿真时间设置为150 s(共计1.5e+04个符号);跳频点数N=64,经反复研究跳频速率Rh与误码率Pe关系之后,确定当数据率Ra=100 bit/s时,跳频速率Rh=50 跳/s 为最佳。模型中采用示波器观察收发数据波形,如图4所示。从示波器收发二进制数据波形来看,对比发送波形,接收端解调输出波形有一个码元时间的延迟(接收波形已设置相应延时)。仿真结果所得误码率Pe=0;增加系统单次仿真时间至300 s,收发数据波形仍然一致,所得Pe仍然为0;再次增加系统单次仿真时间至600 s,收发数据波形仍然一致,所得Pe=0.0001。仿真结果说明:跳频点数N=64,Rh=50跳/s 时,跳频系统抗高斯噪声和抗单频干扰性能优异。

图4 跳频系统收发数据波形
(2)频谱分析
对系统模型各关键点的信号频谱进行观察和分析。图5是跳频通信系统各关键点信号频谱图(即功率谱)的对比。图a~d 依次为2FSK 已调信号频谱、发送端扩频调制后的信号频谱、接收端扩频解跳前的信号频谱(含单频干扰和高斯噪声)以及接收端解跳后的信号频谱。图2 模型中,2FSK 基带调制的频率间隔为150 Hz,数据率Ra=100 bit/s,由2FSK 原理可知已调信号频谱应为非独立双峰(见图5a)[4]。经扩频调制后,扩频信号频谱的带宽为50×64=3200 Hz(图5 b 的两虚线之间)。接收端解跳前的扩频信号则附加了高斯噪声和单频正弦干扰,单频正弦波频率为200 Hz,有用信号淹没在干扰和高斯噪声之中(见图5 c)。接收端解跳后的信号频谱中,非独立双峰的2FSK 已调信号频谱清晰可见,扩展频谱带宽内的高斯噪声以及单频干扰仍然存在,但完全不影响通信(见图5 d)。

图5 系统各关键点信号频谱分析
(3)跳频速率Rh与误码率Pe关系
通过理论分析和计算,分别设置Rh为25、50、100以及200 跳/s 时,参数设置及误码率见表1。单次仿真时间均为300 s。四种跳频速度下,分别执行跳频系统仿真模型,所得误码率结果,如图6所示。

表1 跳频系统跳频速率Rh与误码率Pe关系
结果表明:对于数据率Ra=100 bit/s,跳频速度Rh<50 跳/s 时误码率Pe=0;当Rh>100 跳/s 时,接收端开始出现误码,执行一次仿真,共得30 000 个符号,误码46 个,Pe=0.0015,如图6c图所示;且随着跳频速率增大,系统误码率呈现迅速增加的态势。
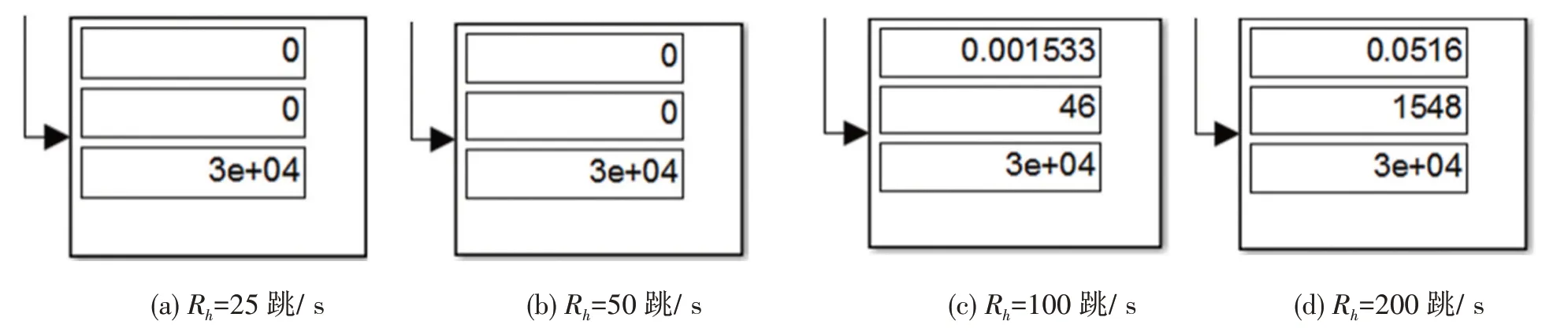
图6 不同Rh时单次执行仿真所得系统误码率
4 结语
跳频通信是扩频通信的一种,具有很多优点。在抗干扰、移动通信、无线局域网、室内无线通信、卫星通信、水下通信、雷达、微波等领域都有广泛的应用。文章首先阐述了跳频通信系统的组成以及相关原理,其次利用Mat-lab/Simulink 仿真平台,设置系统仿真环境的采样率为4 000 次/s。对跳频通信系统进行Simulink 系统建模、频谱分析,并重点对跳频速率Rh与误码率Pe的关系进行了研究。结果表明:对于数据率Ra=100 bit/s,跳频速度Rh<50 跳/秒时误码率Pe=0;当Rh>100 跳/秒时,接收端开始出现误码,Pe=0.001 5,且随着跳频速率的增大,系统误码率呈现迅速增加的态势。
