4种人工晶体度数计算公式预测短眼轴白内障患者术后屈光度的准确性分析

杨智，史庆成，吴海娟，周衍文*

（1.沈阳爱尔眼视光医院白内障科，辽宁 沈阳 110003；2.康平爱尔眼科医院综合眼病科，辽宁 沈阳 110500）

随着现代白内障手术技术和人工晶体制造技术的进步及光学生物测量手段的出现，显著降低了手术操作和术前测量对术后屈光误差的影响[1-3]。而选择理想的人工晶体度数计算公式，成为减少术后屈光度误差的关键方法之一。在正常范围眼轴眼中，绝大多数病例预测偏差＜1.0 D[4]。但在短眼轴眼中，因其解剖结构的特殊性，术前不能精确推测术后人工晶体在眼内的位置（the effective lens position，ELP），且短眼轴眼中植入的人工晶体屈光度较高，导致预测误差更大[5]。比较各公式预测短眼轴白内障患者术后屈光度的准确性，国内外研究结果不一致[6-10]。本研究对眼轴＜22 mm 的患者术后屈光误差进行对比，比较Barrett UniversalⅡ、SRKT、Hoffer Q和SRK-Ⅱ4种公式的预测准确性，旨在为短眼轴白内障患者选择最适宜的人工晶体公式提供借鉴和参考，现报道如下。

1 资料与方法

1.1 临床资料 回顾性分析2018 年6 月至2019 年8 月沈阳爱尔眼视光医院收治的短眼轴眼（眼轴＜22 mm）白内障超声乳化术联合人工晶体植入术患者18例（18只眼），男4例，女14例，年龄55～86岁，平均（73.4±9.4）岁；病程3～60个月，平均[6（4，13.5）个月]。本研究经沈阳爱尔眼视光医院医学伦理委员会审核批准。

纳入标准：①全部患者眼轴＜22 mm，平均眼轴（21.55±0.44）mm；②晶状体混浊程度依据LOCSⅢ系统分级，皮质混浊＜C4，核混浊＜N4，后囊下混浊＜P3[11]。排除标准：①角膜云翳；②青光眼；③严重眼底病变；④翼状胬肉；⑤既往眼部手术史；⑥严重晶体混浊不能用IOL Master 测量等患者；⑦术中及术后复查期间发生手术相关并发症。

1.2 方法 术前常规行裂隙灯显微镜检查、90D前置镜眼底检查、A超、B超、眼压、角膜地形图以及角膜内皮镜检查等。利用IOL Master（德国Carl Zeiss公司）测量眼轴长度（axial length，AL）、角膜曲率（keratometry，K）、前房深度（anterior chamber depth，ACD），晶体厚度（lens thickness，LT），白到白（white to white，WTW）等数据。依据患者生活和工作中用眼习惯，IOL Master内置软件用SRK-T、Hoffer Q和SRK-Ⅱ公式计算所用人工晶体的预期屈光度，同时将测得的数据代入在线计算公式Barrett UniversalⅡ，得出预期屈光度。手术均由同一位资深医师进行，采用2.2 mm 110°角膜缘切口植入可折叠式后房型IOL于囊袋内，光学面居中。

1.3 观察指标及评价标准 术后1 个月复查时进行电脑验光及主观验光，获取患者最佳视力的等效球镜度，将实际术后屈光度减去预期屈光度得到的数值的绝对值作为绝对屈光度误差（absolute refrac-tive error，AE），其均值为平均绝对屈光度误差（mean absolute refractive error，MAE）。计算并比较各公式的MAE，并观察各公式MAE的影响因素。

1.4 统计学方法 采用SPSS 17.0统计学软件进行数据分析，对数据进行正态性检验，符合正态性分布和方差齐性的数据采用F分析，不符合正态分布者转换为正态分布后行统计学分析，以P＜0.05 为差异有统计学意义。对于误差的影响因素分析采用多元线性回归分析，以P＜0.05 为差异有统计学意义。

2 结果

2.1 4 种公式的MAE 总体比较 Barrett UniversalⅡ公式与另外3 种公式比较误差最小，差异有统计学意义（P=0.022），见表 1。Barrett Universal Ⅱ、SRK-T、Hoffer Q 和 SRK-Ⅱ4 个公式误差范围在±0.5D 以内的比例分别为44.4%、33.3%、38.9%、27.8%，在±1.0 D 以内的比例分别为66.7%、61.1%、61.1%、61.1%。

表1 4种公式平均绝对屈光度误差比较（D）Table 1 Comparison of average absolute diopter error of four formulas(D)

2.2 各公式误差的影响因素分析 利用多元线性回归方法对各公式误差的影响因素进行分析，包括AL、ACD、K值、LT及WTW。SRK-T公式误差的独立影响因素为AL（F=3.417，P=0.041），AL减少会增加预测误差、降低公式的准确性，见表2；SRK-Ⅱ公式误差独立影响因素为AL（F=3.849，P=0.026），AL减少会增加预测误差，见表3；Hoffer Q 公式误差的独立影响因素为 AL 和 ACD（F=3.629，P=0.031），AL 减少及前房深度的增加会加大预测误差，见表4；Barrett UniversalⅡ公式的预测准确性不受上述因素的影响（F=0.862，P=0.533），见表5。

表2 SRK-T影响因素的多元线性回归分析Table 2 Multiple linear regression analysis of influencing factors for SRK-T

表3 SRK-Ⅱ影响因素的多元线性回归分析Table 3 Multiple linear regression analysis of influencing factors for SRK-Ⅱ

表4 Hoffer Q影响因素的多元线性回归分析Table 4 Multiple linear regression analysis of influencing factors for Hoffer Q

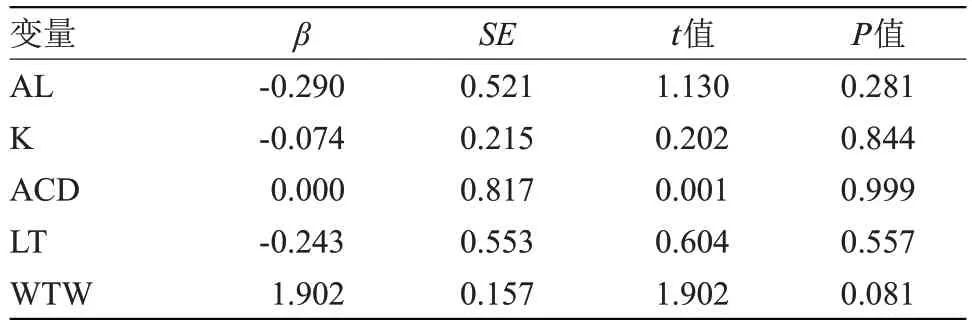
表5 Barrett UniversalⅡ影响因素的多元线性回归分析Table 5 Multiple linear regression analysis of influencing factors for Barrett UniversalⅡ

3 讨论

眼轴短于22.00 mm 的短眼轴眼术前难以准确评估ELP，可能导致术后远视偏移[8]。有效人工晶体位置（ELP）是指人工晶体植入眼内后的等效光学面的位置。各IOL 度数计算公式均有各自的预测ELP的方法。本研究中使用的4种公式依据ELP的计算方法分为第二代的SRK-Ⅱ公式、第三代的SRK-T 公式和Hoffer Q 公式及最新一代的Barrett UniversalⅡ公式。SRK-Ⅱ公式只是设置了一个调整常数，对不同的眼轴进行校正；SRK-T 公式通过AL、K值以及A常数预测ELP[12]；Hoffer Q公式使用了新的预测参数，有研究认为，该公式在眼轴＜22.00 mm时，准确性较SRK-T公式高[13]。

以往研究对短眼轴眼的IOL计算公式的准确性比较结果不一。Aristodemou 等[4]研究表明，眼轴＜21 mm 患眼，Hoffer Q 公式准确性最高，而＞21 mm患眼，几种公式比较差异无统计学意义。

目前，Barrett UniversalⅡ公式是最新一代的公式，为厚透镜公式，基于近轴光线追迹技术，优势是考虑到不同度数的人工晶状体之间主光学面的差异，预测屈光度与AL、K、ACD、LT 和WTW 等均有关系[14]。关于该公式在短眼轴眼人工晶体度数计算中的表现，在国外已有很多报道[15-16]。

本研究中通过比较SRK-T、SRK-Ⅱ、Hoffer Q和Barrett UniversalⅡ公式计算18 例短眼轴白内障眼术后屈光度的MAE 来观察4 种公式的总体预测误差分布情况。以MAE 作为观察指标，这是为了避免由于计算过程中屈光度的正负值中和导致均值结果偏差。研究结果发现，Barrett UniversalⅡ公式和Hoffer Q 公式预测误差最小，4 种公式比较差异有统计学意义（P＜0.05）。预测误差绝对值＜0.5 D 和＜1.0 D 的百分率，4 种公式比较差异均无统计学意义。影响预测误差的因素中，Barrett UniversalⅡ公式不受 AL、K 值、ACD、LT 及 WTW 的影响，SRK-T、SRK-Ⅱ公式受 AL 影响，Hoffer Q 公式受AL及ACD的影响。说明Barrett UniversalⅡ公式在各种眼轴长度眼、不同前房深度眼、不同角膜曲率眼均表现出良好的预测准确性。

综上所述，对于短眼轴白内障患者人工晶状体度数计算时，4 种公式准确性优劣顺序为：Barrett UniversalⅡ、Hoffer Q、SRK-T、SRK-Ⅱ，且 Barrett UniversalⅡ公式预测稳定性最佳。因短眼轴眼在人群中比例较低，本研究例数相对较少，故有一定局限性，短眼轴眼人工晶状体计算公式的合理选择，需进一步扩大样本量进行深入研究。