基于无迹卡尔曼滤波的柔性自由翻滚目标姿态估计

赵梓良，孙晟昕，李文龙，魏 承

（1.哈尔滨工业大学航天学院，哈尔滨 150001；2.上海卫星工程研究所，上海 200240）

据NASA 官网统计，截至2019 年10 月，太空中已有约19 779 个直径超过10 cm 的航天器和空间碎片［1］。毫无疑问，这些航天器和空间碎片会对未来的航天任务产生巨大的阻碍。因此，回收、清除这类失效航天器和空间碎片成为了时下在轨服务研究的热点。上述空间碎片多为自由翻滚的非合作目标，与空间机器人之间不能够进行信息通讯，目标在空间中的姿态变化不能够准确预知，因此传统的陀螺及星敏感器的测量方法不再适用于非合作目标消旋工况，需对于空间翻滚目标进行状态估计［2］。

当前Kalman 滤波估计作为一种最优估计方法，已被广泛应用于军事和民用众多领域，包括导航制导、雷达目标跟踪、卫星定位和组合导航、工业智能机器人和故障诊断等。常用Kalman 滤波包括扩展卡尔曼滤波、无损卡尔曼滤波、容积卡尔曼滤波以及粒子滤波等。扩展卡尔曼滤波算法对非线性函数采用Taylor 级数一阶或二阶展开，忽略高阶项做近似化处理，但在实际应用中有些非线性方程很难获得或者不存在Jacobi 矩阵，因此该算法一般用于计算量小、维数少的非线性方程中。无损卡尔曼滤波算法是利用采样方法来近似非线性分布。首先利用前一时刻确定的样本集，通过传递函数、量测方程进行无损变换来对目标状态下一时刻的后验概率密度进行近似，未对非线性方程进行线性化处理，非线性方程的高阶项得以保留。因此，该算法对目标的运动状态估计相对更加准确、CPU 计算消耗小、避免角度姿态估计奇异问题，是目前非线性系统中常用的预测估计方法之一。

文献［3］通过建立四元数姿态运动模型和航姿传感器测量模型提出了一种适用于小型无人机姿态估计的四元数扩展Kalman 滤波算法，提高了无人机姿态的控制精度。文献［4］结合非线性自适应算法、最小二乘法及传统卡尔曼滤波器，设计了改进非线性自适应卡尔曼滤波器。文献［5］利用卡尔曼滤波预测模型，研究桥梁变形监测点的布设，基于应变和挠度监测点的监测数据，预测其他相近位置的应变和挠度监测点的实测值。文献［6］提出一种参数化非合作目标相对位姿和惯量参数估计方法，在不同噪声水平下高精度有效地估计出非合作目标的相对位姿和惯量参数。文献［7］在平方根容积卡尔曼滤波的基础上，提出一种基于修正的自适应平方根容积卡尔曼滤波算法，该算法具有在目标状态突变和量测非线性时的良好滤波性能和数值稳定性。文献［8］提出了一种强跟踪容积卡尔曼滤波算法，与标准无迹卡尔漫滤波和容积卡尔曼滤波算法相比，强跟踪容积卡尔曼滤波算法能够适应目标特征时变的情况，明显改善了目标跟踪的精度和稳定度。文献［9］在传统无迹卡尔曼滤波算法的基础上，结合陀螺仪漂移误差模型，使用误差四元数的方法构建无迹卡尔曼滤波的状态方程，选用加速度计和磁强计的输出作观测量构建无迹卡尔曼滤波的量测方程，并通过自适应调整量测噪声协方差矩阵，减小非重力加速度对姿态解算的影响。文献［10］基于卫星姿态运动方程设计了一种线性卡尔曼滤波器，将卡尔曼滤波器与简化观测器思想相结合，进一步提出一种采用简化滤波器思想的姿态敏感器故障诊断律。文献［11］提出了基于自适应容积粒子滤波的车辆状态估计器，该算法状态估计精度高于传统无迹粒子滤波。文献［12］利用惯性导航系统信息增量来对合成孔径雷达导航信息延迟、非等间隔以及合成孔径雷达量测不在惯性导航系统滤波离散间隔上所带来的误差进行修正。文献［13⁃14］将神经网络与卡尔曼滤波融合开展研究。但是上述研究均建立在状态方程可以准确建立的情况下，针对柔性航天器，其动力学模型不确定性很大，其状态方程很难精确建立，因此需要针对柔性航天器的状态预测进行研究。

本文针对带柔性帆板的自由翻滚目标进行无迹卡尔曼滤波算法设计，首先对轴对称航天器进行姿态动力学分析，分析柔性航天器章动运动规律，以四元数和角速度为状态量，在刚性假设下建立其离散形式的动力学模型。然后通过无迹卡尔曼滤波算法对带柔性帆板的航天器进行运动状态预测。最后，使用BP 神经网络对柔性航天器动力学模型进行补偿，改进无损卡尔曼滤波算法提高预测精度。仿真结果表明：使用神经网络可以有效逼近柔性航天器的动力学模型，补偿模型中的不确定性，从而提高无损卡尔曼滤波的预测精度。

1 自由翻滚目标章动运动学模型

1.1 轴对称航天器姿态动力学

对于自由翻滚目标，采用四元数的形式描述其姿态运动，由非合作柔性航天器姿态动力学可得非合作柔性航天器姿态与角速度的关系为

用Lx、Ly、Lz表示轴对称非合作柔性航天器各轴的转动惯量，有Lx=Lz。以轴对称非合作柔性航天器质心为参考点，依据动量矩定理，作用在轴对称非合作柔性航天器质心上的外部力矩F可以用角动量Γ在时间维度的变化率来进行如下

1.2 柔性航天器动力学模型及章动运动分析

基于轴对称航天器章动运动规律，建立带柔性太阳帆板的轴对称柔性航天器动力学模型（图1），考虑其自由翻滚状态，对柔性航天器章动运动进行仿真，针对不同弹性模量的柔性帆板，分析柔性帆板对航天器章动运动的影响规律。图1 中，m系为参考坐标系，其中心点的位置在航天器外形轮廓的中心；b系为质心参照系，其中心点位置在非合作柔性航天器质量中心；fi系为柔性帆板的本体坐标系，其中f1系为沿着b系正y向分布的柔性帆板本体坐标系，f2系为沿着b系负y向分布的柔性帆板本体坐标系。

图1 带柔性帆板的轴对称航天器Fig.1 Axisymmetric spacecraft with flexible sails

对于含双侧柔性帆板的柔性航天器建立拉格朗日方程

式中：下标i=1，2 代表两侧帆板；X为质心在惯性系下投影；M为整星质量，M=Mb+Mf1+Mf2，其中，Mb为航天器质量，Mfi为柔性帆板质量；ωai为柔性帆板相对中心刚体的相对转速矢量；Pi描述了柔性帆板转动和柔性非合作航天器本体平动之间的刚性耦合关系；Ftai描述了柔性帆板振动和柔性非合作航天器本体平动之间的柔性耦合关系；Rsai描述了柔性附件转动同基体转动之间的刚性耦合关系；Fsai和Fai分别描述了柔性帆板振动与柔性非合作航天器本体姿态、另一侧柔性帆板之间振动的柔性耦合关系；Jfui为柔性帆板初始未变形时刻相对柔性帆板本体坐标系原点的转动惯量；Ji表示整星相于非合作柔性航天器质心的转动惯量在非合作柔性航天器质心坐标系下的投影，有

式中：rai为质心在非合作柔性航天器质心坐标系的投影；Ci为柔性帆板本体坐标系与非合作柔性航天器质心坐标系间的坐标变换矩阵；ρci为柔性帆板i的铰接点指向其质心的位置矢量在柔性帆板本体坐标系fi下的投影。并且由于非合作柔性航天器系统质心特性，非合作柔性航天器本体平动和转动之间的耦合抵消。

将式（8）展开写成如下分量形式

表1 为柔性航天器的主要状态参数。非合作柔性航天器以Y轴为主自旋轴，自旋轴角速度为1 rad/s，章动角为0.528°。

表1 柔性航天器状态参数

Z轴方向的自旋角速度为惯性主轴角速度，当柔性帆板的弹性模量取值为0.5×108Pa 时，帆板振动频率曲线如图2 所示，柔性太阳帆板的振动收敛速度随弹性模量的增大而变快，而柔性航天器的主自旋轴角速度随着弹性模量的增加衰变程度变小，章动运动状态下柔性太阳帆板的自旋轴角速度在运动初期由于柔性帆板的影响会出现振动现象，运动一段时间后航天器的质量特性不再发生变化，继续按照上文推导的轴对称航天器姿态动力学规律进行运动。

图2 章动各轴角速度变化Fig.2 Change in angular velocity of each axis of chapter motion

2 基于UKF 的柔性航天器状态预测

对章动状态的柔性非合作航天器分别进行无迹卡尔曼滤波估计，采用相同的初始参数，对比两种方法对处于章动状态的柔性航天器的预测效果，验证UKF 对柔性航天器状态预测的精确度。进一步，构建BP 神经网络补偿柔性航天器动力学模型提高预测精度。

2.1 状态方程与量测方程

状态方程和量测方程为

2.2 无迹卡尔曼滤波算法

Sigma 点生成和权重系数计算方法为

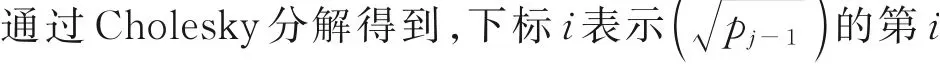
式中：随机变量的分布影响β取值，而β用于调整协方差的近似精度，随机变量分布为高斯正态分布时，β=2。

UKF 算法的基本流程图如图3 所示。

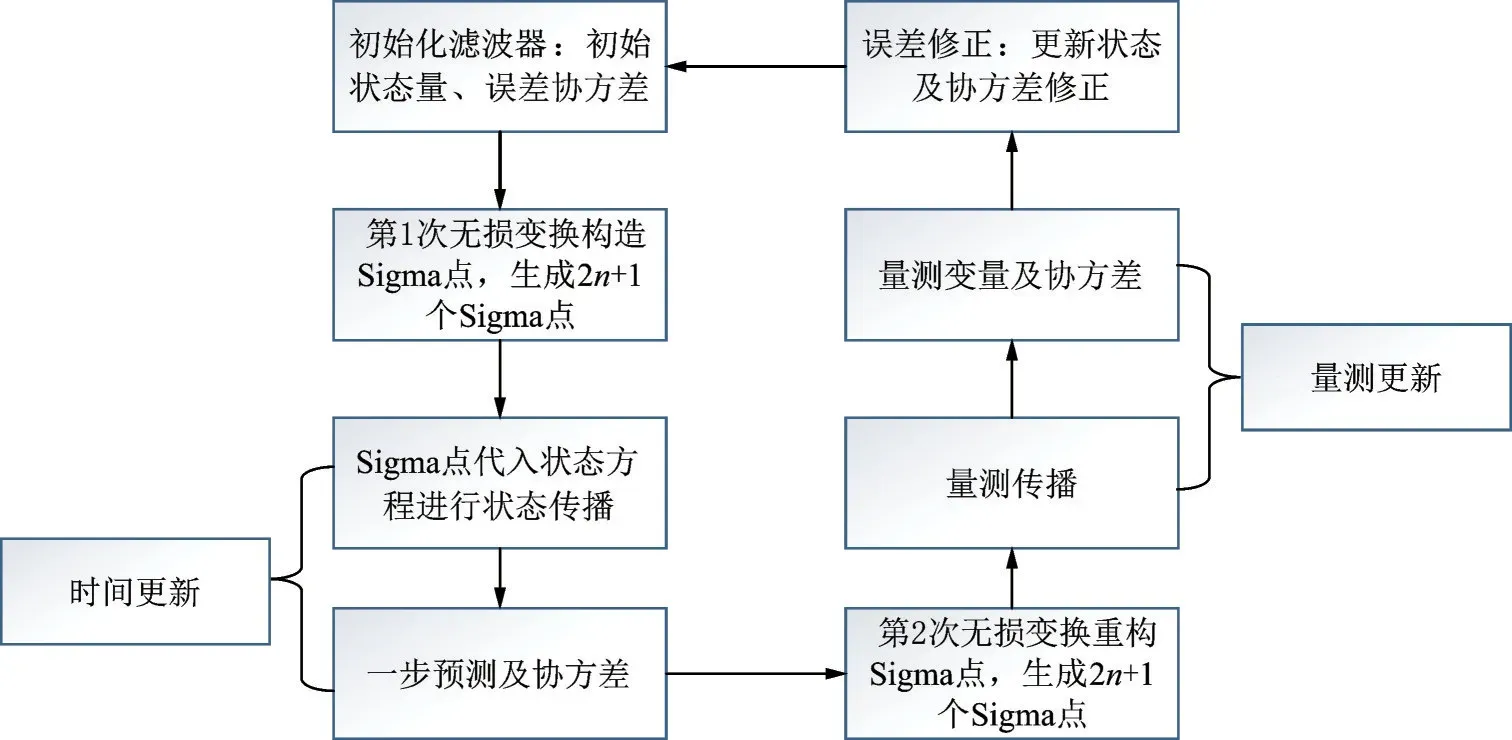
图3 无迹卡尔曼滤波算法流程Fig.3 Traceless Kalman filtering algorithm flow

2.3 基于神经网络补偿柔性航天器动力学模型

在实际应用中，针对含柔性帆板航天器动力学模型中存在的质量特性变化的问题，提出基于BP神经网络的对状态方程进行逼近的方法。引入BP神经网络在线更新来对建模误差、柔性振动问题等不确定项逼近，补偿不确定项对状态方程的干扰，提升滤波器的预测效果。

3 仿真分析

前文已经完成了模型和算法的建立，本节对章动柔性非合作航天器的运动状态进行无迹卡尔曼滤波方法预测，首先对柔性非合作航天器的章动运动状态和滤波器进行初始参数设计，如表2 所示。

表2 初始参数设计Table 2 Initial parameter design

根据上文设定的初始参数对柔性航天器的姿态四元数和角速度进行无迹卡尔曼滤波预测，仿真步长设定为0.1 s。由无迹卡尔曼滤波得到的四元数和角速度误差如图4 所示。

由图4 可知，无迹卡尔曼滤波算法对柔性航天器的姿态四元数预测误差值在10-3范围内，在对角速度的预测上误差较大，其中自旋轴的误差最大，误差值在运动初始阶段达到了0.08 rad/s，运动稳定后误差在10-2范围内。

图4 无迹卡尔曼滤波算法误差Fig.4 Traceless Kalman filtering algorithm error

由于太阳帆板的柔性特性，运动初期航天器的转动惯量会持续变化，导致滤波器在动力学模型不精确的情况下得到的预测误差极大。采用神经网络对带有柔性帆板的航天器进行动力学模型逼近以减小预测误差。使用基于大量训练样本学习后的神经网络代替式（8）中的状态函数，其余步骤不变，得到四元数、角速度误差如图5 所示。采用神经网络补偿不确定的动力学模型后，UKF 的四元数误差稳定在9×10-4范围内，角速度误差稳定在1.5×10-3范围内。根据上文分析可知，状态传播矩阵中对四元数的动力学模型描述很精确，而角速度对应的动力学模型由于转动惯量的变化其精度很差。因此，采用神经网络补偿动力学模型后滤波器对角速度的预测精度提高了很多，而四元数的预测误差并未有大幅度的下降。

图5 基于神经网络动力学模型补偿的无迹卡尔曼滤波Fig.5 Traceless Kalman filtering based on neural network dynamics model compensation

4 结论

本文研究了基于无迹卡尔曼滤波算法的带柔性帆板的自由翻滚目标姿态预测方法。以四元数和角速度为状态量建立其离散形式的动力学模型，使用BP 神经网络对柔性航天器动力学模型进行补偿。使用在刚性假设条件下的动力学模型作为状态方程时，姿态四元数预测误差值在10-3范围内，角速度预测误差值最大达到了0.08 rad/s，使用神经网络补偿动力学模型的不确定项后，四元数误差稳定在9×10-4范围内，角速度误差稳定在1.5×10-3范围内。可以得出结论，使用神经网络可以有效逼近柔性航天器的动力学模型，补偿模型中的不确定性，大幅度地提高UKF 的预测精度。