塑性区对增材制造316L 多轴缺口疲劳影响研究

王英玉，董星亮，龚 帅，姚卫星

（南京航空航天大学飞行器先进设计技术国防重点学科实验室，南京 210016）

增材制造（也称为3D 打印）是一种新型的、具有巨大发展潜力的先进制造技术，不同于传统的机械加工技术，该技术通过逐层增加材料的方式实现零部件的成型，在加工过程中不受刀具和零部件结构的限制，能够制造出传统机加工方式难以甚至无法制造的复杂零部件，并可以将材料成型与结构设计优化结合起来，即实现制造和拓扑优化的协同［1⁃3］。随着科学技术的进步和经济社会的发展，增材制造越来越受到人们的重视，国内外对增材制造技术做了大量的研究，并且在一些领域实现了工程应用。增材制造技术的权威发展报告“Wohlers Report”指出，增材制造技术带来的结构轻量化和结构一体化成型的优势，使其有望在航空航天领域最先得到突破性应用［4］。国内外主要的航空航天企业和科研院所都开展了针对重要零部件的增材制造研究和应用试验。波音、空客、洛克希德·马丁、诺斯罗普·格鲁曼和通用电气等世界著名航空航天企业研发了增材制造的翼梁、翼肋、舱隔板、航空发动机叶片、燃油喷嘴、高压油箱和火箭发动机喷管等零部件产品［5⁃9］。国内的大型航空航天企业和科研院所也研制出了增材制造的飞机加强框、风挡整体窗框、中央翼缘条和球形燃料贮箱等零部件［9⁃12］。

增材制造零部件有别于传统机加工零部件，其加工成形方向、表面粗糙度及内部孔洞等因素均会对其疲劳性能产生影响。针对增材制造材料的疲劳性能，国内外专家学者做了一些研究。Kumar等［13］研究了使用粘合剂喷射打印（Binder jet print⁃ing，BJP）和选区激光熔化（Selective laser melt⁃ing，SLM）制成的316L 奥氏体不锈钢的显微组织和疲劳强度，并将其与常规制造（Conventionally manufactured，CM）合金进行了对比。Falkowska等［14］针对孔隙率不同的316L 不锈钢烧结体，提出了一种线性和非线性的疲劳损伤累积模型。其损伤状态变量的增量取决于塑性应变的增量、法向应力的值和损伤状态变量自身的值。该研究发现不同的孔隙率不会影响材料中损伤累积的特性，而只会影响其累积速率。吴剑平［15］对选区激光熔化316L 不锈钢试验件进行了单向拉伸试验以及疲劳裂纹扩展试验，研究了部分工艺参数（成型角度和能量密度）对该材料疲劳裂纹扩展性能的影响。另外一些学者［16⁃21］研究了微观组织和微观缺陷对增材制造金属材料疲劳性能的影响。

在工程实际中，由于载荷的复杂性，结构服役期间通常都受到多轴载荷的作用。另外，由于工程构件中往往存在开口、凹槽、凸台、弯折和分叉等结构不连续处，这使得其即使在承受单向载荷时，结构部分区域也有可能处于多轴应力应变状态。目前，在缺口件的多轴疲劳研究领域还未形成统一的理论，人们从不同的观点出发，提出了各种不同的疲劳寿命预测方法。其中，名义应力法［22⁃23］和局部应力应变法［24⁃25］在工程上应用较多，但由于对缺口效应的考虑不足，导致这两种方法疲劳寿命预测精度较差。临界距离法［26⁃27］和应力场强法［28］精度较高，但计算过程复杂，不便于工程应用。

最近几年，国内外一些学者在前人研究成果的基础上提出了新的缺口件多轴疲劳寿命预测方法。Gallo 等［29］对具有不同理论应力集中系数的316L 不锈钢缺口圆棒试件进行了多轴疲劳试验后发现，疲劳裂纹由缺口尖端萌生并沿径向扩展。基于此发现，通过考虑缺口尖端附近的应变梯度和最大有效应变变程，提出了一种新的寿命预测模型。Liao 等［30］将临界面法和临界距离法结合起来，提出了新的缺口件多轴疲劳寿命预测方法，通过对比疲劳寿命预测结果发现，将临界距离定义为与疲劳寿命相关的函数可以获得更高的疲劳寿命预测精度。Luo 等［31］将临界面法和临界距离法组合运用于拉扭多轴载荷下薄壁开孔缺口件的疲劳寿命预测，较为准确地预测了疲劳裂纹的萌生位置和扩展方向，但该方法的寿命预测精度仍有待提高。钟波等［32］针对缺口效应引起的应力梯度提出了等效应力梯度因子，并在此基础上提出了一种新的考虑应力梯度影响的多轴缺口件疲劳寿命预测方法。谭晶莹等［33］根据剪应力随距缺口根部距离的变化趋势确定有效损伤距离，采用体积法进行寿命预测，并获得了较高的预测精度。Razavi 等［34］、Branco等［35］和Meneghetti 等［36］将缺口根部附近特定区域内应变能密度特征值作为疲劳损伤参量，结合主寿命曲线预测缺口件的多轴疲劳寿命。

目前，国内外对增材制造材料疲劳寿命分析的公开报道较少，而对多轴载荷下增材制造金属缺口件的疲劳寿命分析研究更是鲜有报道。在开展材料内部孔洞对增材制造金属材料疲劳性能影响研究［16⁃17］的同时，希望从不同角度深入研究增材制造金属材料疲劳性能。因此，本文从宏观力学角度，开展了增材制造316L 不锈钢光滑件和缺口件的单轴和多轴疲劳试验及弹塑性有限元分析，研究了缺口根部塑性区与缺口几何尺寸、载荷水平和载荷路径的关系，在此基础上提出了缺口根部塑性区的表征方法，并对缺口根部塑性区与疲劳寿命的关系进行了研究。

1 缺口件多轴疲劳试验

1.1 试验件材料和设计

1.1.1 试验件设计

试验件分为光滑试验件和缺口试验件，其中，缺口试验件又分为V 形缺口试验件、R2 缺口试验件和R5 缺口试验件，各种试验件的形状和尺寸如图1 所示。

图1 试验件几何形状与尺寸Fig.1 Geometry and dimensions of specimens

1.1.2 试验件材料

试验件的材料是316L 不锈钢，采用选区激光熔化技术制备，使用450 W 的激光功率和1 500～2 000 mm/s 的扫描速度熔化样品粉末，扫描间距为0.05 mm，成型方向为试验件的长轴线方向，如图2 所示。在选区激光熔化成型之后对试验件进行退火处理，退火温度为490 ℃，时间为6 h，采用氩气冷却。最后通过机加工获得所需的试验件外形并将试验段表面抛光至表面粗糙度为0.05 μm的镜面。对光滑试验件进行准静态单向拉伸试验，获得了该材料在室温下的拉伸应力⁃应变曲线和基本机械性能数据，如图3 和表1 所示。

图2 试验件成型方向示意图Fig.2 Schematic of specimen orientations

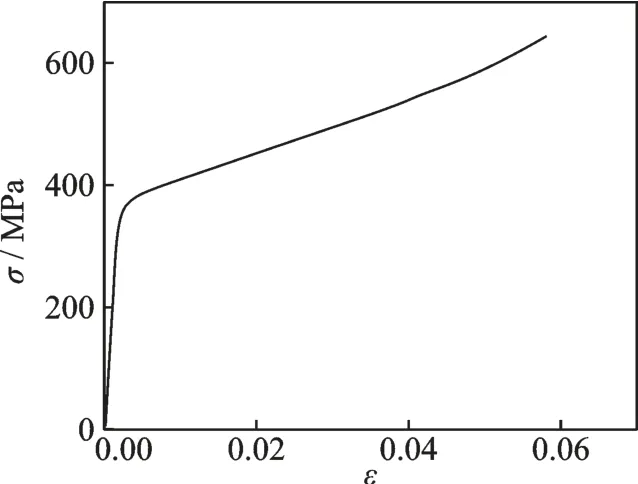
图3 选区激光熔化316L 不锈钢在室温下的拉伸应力-应变曲线Fig.3 Stress-strain curve of selective laser melting 316L stainless steel under tensile at room temperature

表1 选区激光熔化316L 不锈钢的机械性能Table 1 Mechanical properties of selective laser melting 316L stainless steel

1.2 试验方法和结果

1.2.1 试验介绍

所有试验均在MTS 809 拉扭电液伺服疲劳试验机上进行，试验环境为室温和空气，疲劳寿命定义为试验件断裂时对应的载荷循环数。单轴疲劳试验采用轴向力控制，多轴疲劳试验采用轴向力和扭矩同时控制。试验件标距段的轴向应力幅值和表面剪应力幅值依据以下3 个等式计算

式中：σa为标距段的轴向应力幅值，τa为标距段的表面剪应力幅值，F为施加在试验件上的轴向力，M为施加在试验件上的扭矩，r为光滑试验件标距段的平均半径（或者缺口试验件缺口处最小横截面的半径），λ为轴向应力幅值和剪应力幅值的比值。疲劳试验载荷波形为等幅正弦波，应力比R=-1，平均应力为零，试验中任一时刻的瞬时加载应力表达式为

式中：σ(t)和τ(t)分别为瞬时轴向应力和瞬时表面剪应力，ω为加载角频率，t为试验时间，φ为在试验件上加载的轴向应力和剪应力波形之间的相位差，σeq(t)为任一时刻试验件上加载的von Mises 当量应力。

根据研究目的，选取疲劳试验加载路径如图4所示。

图4 疲劳试验加载路径Fig.4 Stress loading paths

1.2.2 疲劳试验结果

单轴疲劳试验结果如图5 所示，多轴疲劳试验结果如图6 所示。在单轴和多轴载荷下，各结构形式试件的疲劳寿命均随着载荷幅值的提高而减小。在多轴载荷下，拉应力幅值一定时，缺口试验件的疲劳寿命随着缺口半径增大而增大。

图5 单轴疲劳试验结果Fig.5 Uniaxial fatigue test results

图6 缺口件多轴疲劳试验结果Fig.6 Multiaxial fatigue test results of notched specimens

2 弹塑性有限元分析

对光滑件、V 缺口件、R2 缺口件和R5 缺口件进行了弹塑性有限元分析，为了避免文章繁冗，以V 缺口件为例进行阐述。

2.1 有限元建模

由于试验件是旋转体，为了提高计算精度和计算效率，采用轴对称有限元分析方法。有限元分析采用ABAQUS 软件，选择含扭转的轴对称四边形单元CGAX4R，为了提高缺口根部应力应变分析的精度，将缺口根部径向1 mm 细化为400 个单元，对该V 缺口件的二维模型划分网格，得到节点数为22 820，单元数为22 140，网格划分结果如图7所示。

图7 V 缺口件的网格划分Fig.7 Meshes of the V-notched specimen

将准静态拉伸试验获得的应力⁃应变曲线输入有限元模型，选用多线性随动强化模型和von Mis⁃es 屈服准则，以便于准确模拟材料的应力应变状态。对应于疲劳试验的加载方式，将试验件有限元模型的一端固定，在另一端施加拉⁃扭循环载荷。最后，利用ABAQUS 求解器进行有限元计算。

2.2 有限元分析结果

对输出的结果进行后处理即可得到该有限元模型上各单元和各节点在某些特定循环数下的应力应变数据，如图8 所示。由有限元分析结果可知，在所研究的90°非比例载荷下，V 缺口件在3 级载荷水平时均存在塑性区，R2 缺口件和R5 缺口件在3 级载荷水平时均不存在塑性区，因而无法研究其塑性区与载荷和缺口的变化关系，故本文未列出R2 缺口件和R5 缺口件在90°非比例载荷下的塑性区图像。

图8 弹塑性有限元分析结果示例Fig.8 Example of elasto-plastic finite element analysis re⁃sults

（1）缺口几何尺寸对塑性区影响

在相同轴向应力幅值σa的比例加载下，对不同类型缺口件的弹塑性有限元分析结果进行比较，如图9 所示。V 缺口的塑性区形状受缺口的影响较大，塑性区呈现出不规则的几何形状，R2 缺口和R5 缺口则由于缺口根部曲率较小，缺口效应较弱，其塑性区边界接近圆弧形。在较高的载荷水平下，R5 缺口塑性区最大，R2 缺口塑性区次之，V 缺口的塑性区最小；随着载荷水平的降低，3 种缺口的塑性区面积逐渐接近，随着载荷水平的进一步降低，R5 缺口和R2 缺口的塑性区迅速减小或消失，三者的塑性区面积大小顺序对调。

图9 缺口几何尺寸对塑性区影响对比(φ=0°)Fig.9 Comparison of influence of notch geometry on plastic region (φ=0°)

（2）载荷水平对塑性区影响

图10 为在不同轴向应力幅σa的比例加载下，各类型缺口塑性区比较结果。各类型缺口塑性区随着载荷水平的提高而增大，在此过程中，基本保持了其在各类型缺口下的形状特征。载荷水平较低时，V 缺口的塑性区相对较大，R2 缺口和R5 缺口的塑性区较小，甚至没有塑性区，此时，V 缺口塑性区面积最大，R2 缺口次之，R5 缺口的塑性区面积最小。随着载荷水平的提高，V 缺口的塑性区面积增长较慢，R2 缺口次之，R5 缺口的塑性区面积增长最快，在较高的载荷水平下，R5 缺口的塑性区面积最大，R2 缺口居中，而V 缺口塑性区面积最小。此外，在非比例加载时，缺口附近塑性区的面积小于同水平试验载荷下的比例加载情况。非比例加载下，缺口附近塑性区的其他特征与比例加载时相同或接近。

图10 载荷水平对缺口塑性区的影响(φ=0°)Fig.10 Comparison of influence of stress amplitude on plas⁃tic region (φ=0°)

（3）载荷路径

按疲劳试验载荷的施加方案，选取3 级载荷，每一级载荷又分为不同的相位差，对V 缺口件进行弹塑性有限元分析，得到缺口纵剖面的塑性区如图11 所示。在同一载荷水平下，随着相位差增大，塑性区面积减小，尤其是相位差大于60°时，随着相位差进一步增大，缺口塑性区的面积迅速减小，相位差为90°时，缺口塑性区的面积最小。此外，相位差较小时缺口塑性区边界的形状不规则，随着相位差增大，缺口塑性区的边界逐渐接近圆弧。

图11 相位差对缺口塑性区的影响Fig.11 Comparison of influence of phase lag of loading on plastic region

3 缺口根部塑性区表征方法

本节基于缺口几何尺寸、载荷水平和载荷路径对von Mises 屈服准则下的缺口附近塑性区的影响，提出了缺口塑性区的表征方法。

在同一名义应力的作用下，缺口件的疲劳寿命通常小于光滑件的疲劳寿命，这是由于缺口效应使得缺口根部应力较大，且局部应力应变场复杂，较大的应力和较复杂的应力场则容易导致缺口根部出现塑性区，塑性区内不可逆的塑性应变加速了材料的疲劳损伤累积并最终导致材料疲劳断裂。因而，缺口塑性区的面积是反映缺口件疲劳损伤的重要参数之一。

利用完全弹性有限元分析方法求得本文研究的缺口件单轴拉伸时的理论应力集中系数如表2所示。通过对更多具有不同理论应力集中系数的缺口件进行多轴加载下的弹塑性有限元分析，可得各缺口件开始出现塑性区时的临界拉应力幅值σa，c（单位：MPa）与理论应力集中系数KT的关系，如表3 和图12 所示，得到关于临界拉应力幅值σa，c与理论应力集中系数KT和拉扭载荷相位差φ的函数关系式为

表2 单轴拉伸下的理论应力集中系数Table 2 Theoretical stress concentration factors under uniaxial tension

表3 多轴载荷下缺口应力集中系数与对应的临界拉应力幅值Table 3 Stress concentration factors of notches and cor⁃responding critical tensile stresses amplitude under multiaxial fatigue loading

图12 多轴载荷下临界拉应力幅值σa,c 与理论应力集中系数KT关系曲线Fig.12 Relationship curve of critical tensile stress ampli⁃tude σa,c and the theoretical stress concentration fac⁃tor KT under multiaxial fatigue loading

由对缺口塑性区的研究可知，缺口塑性区的形状和面积随着缺口几何尺寸、载荷水平以及载荷路径而变化，且其形状和面积变化对疲劳损伤的影响难以直接衡量。考虑到随着载荷水平的降低，缺口塑性区的实际形状逐渐趋于半圆形；另外，由于疲劳裂纹总是从缺口根部萌生，随后沿着径向正半轴扩展，因此，在x轴的负半轴区域内，随着与缺口根部距离增大，该区域的应力应变状态对缺口疲劳损伤累积的影响迅速减小。假设疲劳破坏区是以缺口根部为圆心的圆或椭圆［28］，为了便于研究，忽略x轴负半轴区域，假设缺口的表征塑性区是以缺口根部O点为圆心，以Rp为半径的半圆，如图13 所示。缺口表征塑性区面积为

图13 缺口的表征塑性区示意图Fig.13 Schematic diagram of characterization plastic region at notch

缺口表征塑性区半径Rp（单位：mm）为轴向应力幅值σa（单位：MPa）、拉扭载荷相位差φ和缺口件理论应力集中系数KT的函数，考虑式（7）和式（8），通过考察载荷水平、载荷路径和缺口理论应力集中系数对缺口根部塑性区面积的影响，并结合有限元分析获得的缺口根部塑性区面积数据进行拟合，得到该函数的解析式如下

︱e︱＜5%，误差在允许范围内。

表4 表征塑性区面积误差分析Table 4 Error analysis on area of characterization plas⁃tic region

4 寿命预测与验证

缺口根部存在应力集中、应力梯度等现象，这些因素共同对缺口构件的疲劳性能产生影响。目前对于缺口件，尤其是增材制造缺口件在多轴载荷下的疲劳寿命预测还没有一个得到普遍认同的方法。本节利用表征塑性区和临界塑性区面积的比值以及缺口根部最大von Mises 应力构造疲劳损伤参量，结合光滑件的单轴S⁃N曲线来预测缺口件的多轴疲劳寿命。

在循环载荷作用下，塑性应变反映出材料已发生不可逆损伤，因此，塑性区的大小和形状对材料的疲劳损伤具有重要影响。实际的塑性区往往呈不规则形状，这导致材料内部塑性区边界附近的应力应变场变得异常复杂，也使得塑性区对缺口疲劳寿命的影响难以直接衡量。由于塑性应变伴随着变形协调现象，对于相同的缺口件有限元模型，弹塑性计算得到的缺口根部最大应力可能远远小于完全弹性计算得到的最大应力。另外，控制缺口疲劳寿命的是缺口根部附近的某一局部区域，而不仅仅是缺口根部的最大应力点，故而考虑利用缺口根部塑性区的大小和形状特征来修正缺口根部的最大von Mises 应力，并将修正后的von Mises 应力作为疲劳损伤参量来预测缺口件的多轴疲劳寿命。为了表征缺口根部塑性区的特征，并建立缺口根部塑性区与疲劳损伤间的联系，提出临界塑性区的概念。

基于前文所述的表征塑性区，临界塑性区也设定为半圆，且与表征塑性区同圆心，如图14 所示。定义缺口根部塑性区边界上任意两点P（xi，yi）和Q（xj，yj），临界塑性区的半径Rp，c为坐标（xi，yi）和（xj，yj）的函数，由于锐缺口（V 缺口）和钝缺口（R2/R5 缺口）的塑性区外形特征不同，该函数的解析式分别为

图14 表征塑性区与临界塑性区示意图Fig.14 Schematic diagram of critical plastic region and char⁃acterization plastic region

在本文研究的中高周疲劳寿命范围内，V 缺口件始终存在塑性区，而R2 和R5 缺口件在90°非比例载荷下其缺口根部出现了无塑性区的情况，此时虽然其缺口根部不存在塑性区，但仍然采用式（13）计算其缺口根部最大von Mises 应力的修正因子f。定义疲劳损伤参量为

由图15 可以看出，基于缺口塑性区影响因子的疲劳寿命预测方法的预测效果较好，预测结果大多在3 倍误差带以内。在较低的载荷水平下，预测结果偏于安全，这表明当应力水平较低时，此方法对缺口塑性区影响因子f和疲劳损伤参量的计算结果略微偏大，导致预测寿命偏小。相对而言，V缺口件的疲劳寿命预测效果最好，预测结果全部位于3 倍误差带内，与V 缺口件的疲劳寿命预测效果相比，该方法对R2 缺口件和R5 缺口件的疲劳寿命预测效果稍差，个别预测结果偏于保守，但仍然在3 倍误差带附近。分析造成该方法对不同类型缺口件疲劳寿命预测精度不同的原因如下：

图15 预测寿命与实验寿命对比图Fig.15 Comparison of experimental and predicted fatigue lives

表5 Basquin 公式的参数取值Table 5 Parameter values of Basquin formula

（1）与R2 缺口和R5 缺口相比，V 缺口的应力集中系数较大，缺口塑性区的应力集中更严重，这导致其缺口根部塑性区和最大von Mises 应力点对疲劳寿命的影响更为明显。

（2）疲劳试验固有的分散性带来的误差。

5 结论

（1）开展了选区激光熔化316L 不锈钢光滑件和缺口件的单轴和多轴疲劳试验。在单轴和多轴载荷下，各结构形式试件的疲劳寿命均随着载荷幅值的提高而减小。在多轴载荷下，拉应力幅值一定时，缺口试验件的疲劳寿命随着缺口半径增大而增大。

（2）基于有限元分析，研究了缺口几何尺寸、载荷水平及载荷路径对缺口根部塑性区的影响。发现在较高的载荷水平下，缺口根部塑性区面积随着缺口根部半径减小而减小；随着载荷水平的降低，3 种缺口的塑性区面积逐渐接近；随着载荷水平的进一步降低，R5 缺口和R2 缺口的塑性区迅速减小或消失，V 型缺口根部塑性区最大。

（3）对缺口根部塑性区进行表征，定义了缺口塑性区影响因子f，应用缺口塑性区影响因子和缺口根部最大von Mises 应力构建缺口疲劳损伤控制参量，并结合光滑件的单轴S⁃N曲线预测缺口件在多轴载荷下的疲劳寿命。经试验验证，该疲劳寿命预测方法具有较高的预测精度。