基于DDPG‑PID 的机器人动态目标跟踪与避障控制研究

刘 勇，李 祥，蒋沛阳，孙博熙，吴 喆，姜 潇，钱 森

（合肥工业大学机械工程学院，合肥 230009）

如何使机器人在完成动态环境下复杂操作任务的同时保证机器人本体不受损害是机器人工程应用中的核心问题。针对这个问题，众多学者展开了如何控制机械臂在复杂工作环境下从初始点运动到目标点并能避开所有障碍物的研究，即避障轨迹规划研究［1］。传统机器人控制方法具有稳定可靠的特点而获得了广泛的应用。祝敬等［2］采用快速搜索随机树方法对人工势场法进行局部改进以解决人工势场法易陷入局部最小点的问题，最后快速有效地规划出一条无障碍的路径。马宇豪等［3］提出了一种基于关节空间的6 次多项式轨迹规划的机械臂避障算法，在机械臂运动学、轨迹长度、关节转动角度等约束下采用多目标优化遗传算法对参数优化获得最优轨迹。Wang 等［4］设计了一种用于空间漂浮7 自由度冗余机械臂的具有避障功能的非线性模型预测控制策略，该策略将避障问题转化为线性不等式约束，并将其集成到二次规划优化问题中。面向动态复杂的操作环境，机器人呈现出工作空间到关节空间映射模型复杂和状态信息误差大的特点，仅使用传统的反馈控制方法进行避障对运动学与动力学及环境模型依赖程度较高，在面对未知可变环境的快速响应方面性能不足。

近年来，随着人工智能的兴起和机器学习的日益发展［5］，衍生出基于强化学习［6］、示教学习和小数据学习的机器人操作方法［7］。将人工智能和机器人技术相结合，使用强化学习为机器人提供框架和工具，从而解决机器人的复杂控制问题［8］。强化学习算法通过利用在马尔可夫决策过程中寻找到的最优策略建立机器人状态与动作间的映射关系，与控制系统决策进行互补以面对复杂多变的操作环境［7］，并且在机器人控制领域取得了一定的成果。李鹤宇等［9］利用DDPG（深度确定性梯度策略）算法控制虚拟环境下的机械臂，实现了相比人工调试更快的抓取动作。Sarantopoulos 等［10］提出了一种具有更快收敛性的模块化的DQN（深度Q网络）算法，并结合DDPG 算法用于实现机械臂将目标从杂物中分离，为抓取目标创造空间。徐帷等［11］针对6 自由度空间机械臂在线路径规划问题，利用Sarsa（λ）强化学习算法实现了目标跟踪及避障的自主路径规划，但在解决具有冗余自由度机械臂的连续运动时可能存在局限性和繁琐性。Christen 等［12］提出了一种具有泛化能力的层次强化学习框架——HiDe，将机器人的复杂控制分解为全局规划和低级控制，DQN 和DDPG 算法分别用于训练规划层与控制层，在仿真中成功控制机械臂推着小球避开障碍物到达目的地。Sangiovanni等［13］通过归一化优势函数，利用基于神经网络的Q⁃learning 强化学习算法控制机械臂，在一个存在不可预知障碍物的连续空间中避开障碍物到达指定位置。

上述基于强化学习的方法虽然能够使机器人具备自主规划能力，但在一般情况下，由于机器人动作空间维数高和状态信息误差大的原因，训练过程可能陷入局部最优或出现学习能力不足的问题。针对这一困境，需恰当地融入先验知识以降低搜索空间维数或提升数据利用率［8］，通过尽可能少的尝试实现机器人强化学习决策。Chatzilyger⁃oudis 等［14］提出了微数据强化学习，该算法可通过在策略结构与参数，期望奖励模型和状态转移动力学模型3 个方面融入先验知识或者构建替代模型实现机器人在数据绝对少的情况下学习到相关策略。Zhong 等［15］设计了一种基于DDPG 算法和机械臂逆运动学的混合算法，用以解决机器人的避障路径规划问题，该算法将机械臂的逆运动学作为一种先验知识融入DDPG 算法，使得其收敛性和收敛速度大大提高。Lin 等［16］考虑到机器人末端轨迹在执行任务中的对称性，结合KER（Kaleido⁃scope experience replay）和GER（Goal⁃augmented experience replay）两种经验回放机制的优势与不足，提出了一个用于在DDPG 算法中实现数据增强的框架——ITER（Invariant transform experi⁃ence replay），实验表明带有数据增强的DDPG 算法可以大大提高机械臂在有障碍和无障碍的情况下学习推、滑和取放物体的效率。

强化学习通过融入先验知识或提高数据质量使得策略网络的性能有所提升，然而这种提升十分有限。众多学者注意到将强化学习算法结合传统控制方法与控制理论能进一步提升算法性能，改善控制效果。一方面，传统控制方法和强化学习算法可以根据机械臂和环境的状态分别对机械臂进行控制，以提高整体控制效果。Johannink 等［17］研究了一种将真实机械臂的复杂控制问题（涉及与环境接触）分解成能用常规反馈控制方法（阻抗控制）有效求解的部分，以及可以用不同强化学习算法求解难以求解的剩余部分，最后叠加两个控制信号得到最终的控制策略。Yamada 等［18］通过基于采样的运动规划器增强的无模型强化学习算法，使得机械臂能够根据动作大小在直接输出单步动作和调用运动规划器之间平滑转换从而提高了机械臂避障轨迹规划的效率和安全性。另一方面，传统控制方法和控制理论可以作为一种辅助手段来从不同方面对强化学习算法进行优化，提高其性能和效率。Al⁃gabalawy 等［19］结合模型预测控制和TRPO（置信域梯度策略优化）算法，构建了一种混合算法以实现机械臂在有环境边界约束和障碍物约束的情况下到达目标位置，该混合算法相比于无模型强化学习算法所需的样本数据更少，性能更高。Kuk⁃ker 等［20］提出了一种基于随机遗传算法辅助的模糊Q⁃learning 的机械臂控制方法，遗传算法作为随机优化器，对基于模糊Q⁃learning 的控制器各阶段的动作选择进行优化。Ota 等［21］提出了一种将TD3（双延迟深度确定性策略梯度）算法与传统快速搜索随机树算法相结合的方法，训练机械臂获得动态平滑且能够避开障碍的最优轨迹，其中快速搜索随机树算法用于指导智能体学习，即限制搜索域以提高算法收敛性和收敛速度。

本文采用DDPG 强化学习算法与PID 控制相结合的方式求解机械臂动态目标跟踪与自主避障的运动策略。一方面，为提升DDPG 强化学习算法的收敛性，本文结合机械臂的机构特性，将目标物与障碍物投影到机械臂的工作平面构建虚拟目标物与虚拟障碍物来降低强化学习动作空间的维数；另一方面，引入传统PID 控制方法来控制机械臂的工作平面快速接近目标，提高目标跟踪与避障的成功率。

1 问题描述和机械臂几何关系分析

1.1 运动路径规划问题描述

如图1 所示的机械臂是一种经典的6 自由度机械臂——UR5 机械臂，其结构包括底座、两个肩关节和一个位于中间的肘关节以及末端3 个腕关节。

图1 UR5 机械臂模型Fig.1 Model of UR5 manipulator

UR5 机械臂的运动由6 个关节所共同控制，每个关节控制的主要目标有所不同。在机械臂的末端加装执行器后，末端关节D、E主要决定了末端执行器在完成特定任务时的姿态，在进行大幅度运动或完成常规的目标抓取等信息捕获任务时，主要依赖于O、A、B、C关节进行快速运动，使末端执行器快速接近目标。本文主要考虑机器人大范围运动目标跟踪的粗捕获任务［11］，将关节D、E固定且在建模过程中引入关节偏置从而更加接近真实机械臂模型，图1 简化后的空间数学模型如图2所示。

图2 机械臂模型简化Fig.2 Simplification of manipulator model

Ox0y0z0是基准坐标系，机械臂的基座底面中心与该坐标系原点O重合，W为经过z0轴与ab杆平行且与x0Oy0平面垂直的机械臂工作平面，由肩关节o的关节角θ1确定。各连杆长度为l1、l2、l3、l4和l5。本文仅考虑两个肩关节o和a、一个肘关节b、一个腕关节d，它们相对于其零位的关节角为θ1、θ2、θ3和θ4。T为目标物，M为障碍物，它们绕z0轴旋转在平面W内的旋转投影构成虚拟目标物T′和虚拟障碍物M′。

机械臂避障路径规划的目标是实现机械臂末端点g从初始位置到达目标物T的位置，同时在整个过程中不与环境中的障碍物M发生碰撞。为实现这一目标，可以将三维空间跟踪避障问题分解：一方面，控制机械臂的肩关节o，使得工作平面可以快速到达目标物所在的平面，同时，目标物T与障碍物M的投影T′与M′一直作为虚拟目标物与虚拟障碍物存在于工作平面W中；另一方面，在平面W中，通过控制关节a、b和d使得机械臂末端点g能够跟踪虚拟目标物T′同时避开虚拟障碍物M′。通过上述两方面的协同控制，最终在三维空间中实现机械臂末端点g跟踪目标物T，同时避开障碍物M。

1.2 平面几何关系分析

如图3 所示，将整个机械臂先投影到工作平面W，在该平面内重新建立坐标系xOy计算机械臂各关节与末端的位置关系。

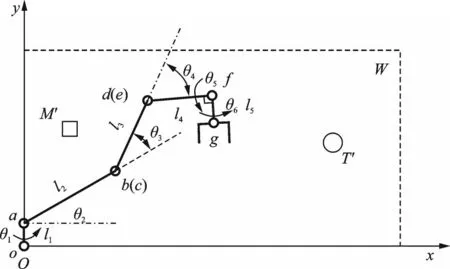
图3 机械臂在工作平面的投影Fig.3 Projection of manipulator on the working plane

关节a、b、d、f及机械臂末端点g在该平面坐标系中的位置关系可表示为

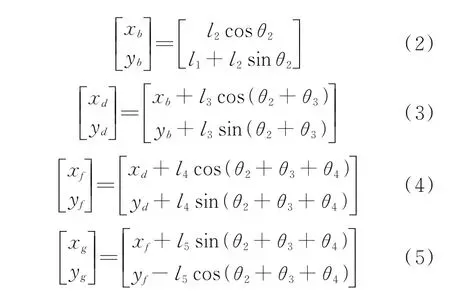
机械臂的工作平面W为一个经过z0轴与ab杆平行且与x0Oy0平面垂直的一个平面，此时机械臂末端点g不在工作平面上，即发生错位从而导致末端点g不能准确与目标物的坐标重合，这是机械臂关节自身宽度导致的。为解决这一问题，本文对关节o的关节角θ1做了偏置处理，即将工作平面W向着g点绕z0轴旋转α度得到一个新的工作平面W′，使得末端点g在工作平面上。选用工作平面W′，一方面可以使得PID 对关节o的控制（即对工作平面的控制）更加直接，简化后续目标物的投影转换；另一方面可以平衡工作平面两侧UR5 机械臂的构型分布以简化对避障方法的设计。偏置只会影响肩关节o的角度变化，不影响强化学习算法对a、b和d关节的控制。针对UR5 机械臂构型特点，将机械臂向x0Oy0平面进行投影，建立如图4 所示的关节偏置模型。与图2 相比，该模型参考了机械臂的实际模型，关节o与关节a在x0轴方向上存在一个大小为p的偏差。

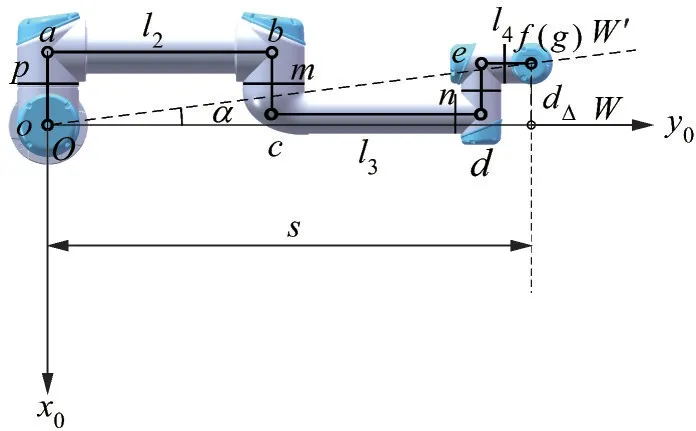
图4 关节偏置Fig.4 Joint offset

偏置距离为

2 强化学习及其状态与奖励函数设计

本文应用DDPG 强化学习算法，将机械臂视为能感知环境状态并输出动作决策的agent，agent的动作a为相应的关节角速度；环境状态s为要实现目标所需要反馈给agent 的各种相关的环境信息；奖励函数R为机械臂agent 在与环境交互过程中所获得的回报，奖励函数的设计非常重要，能直接影响后面学习过程的收敛性。

2.1 DDPG 强化学习算法

DDPG 是一种基于actor⁃critic（演员⁃评论家）框架的强化学习算法，它可以应对agent 需要输出连续动作的问题，更加符合机械臂在状态空间内运动连续的特性，因此本文采用该算法进行求解。图5 描述了DDPG 算法的网络框架，st、rt、at为t时间步的状态、奖励以及动作；μ表示策略，θ为神经网络参数。

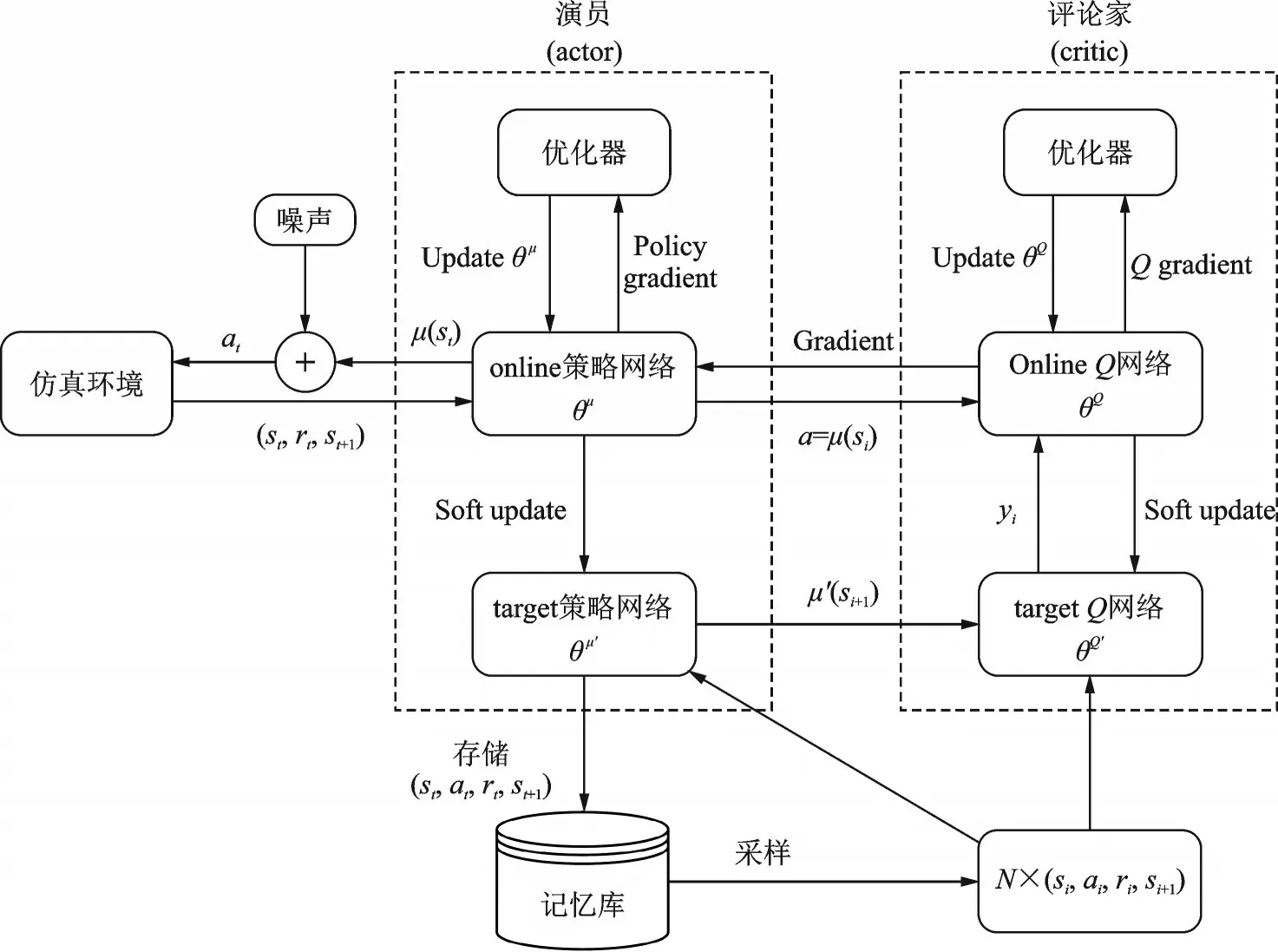
图5 DDPG 算法网络框架Fig.5 Network framework of DDPG algorithm

评论家（critic）网络用于拟合Q函数（价值函数），包含有两个Q神经网络拷贝，online 和target，记为Q(s，a|θQ)和Q'(s，a|θQ′)，两者的参数θQ和θQ′的初始值相同。在训练过程中，当记忆库中的样本数到达设定数值时，则从中提取数量为N的样本：N×(si，ai，ri，si+1)，并通过最小化式（9）所示的损失函数L来更新onlineQ网络的参数θQ。

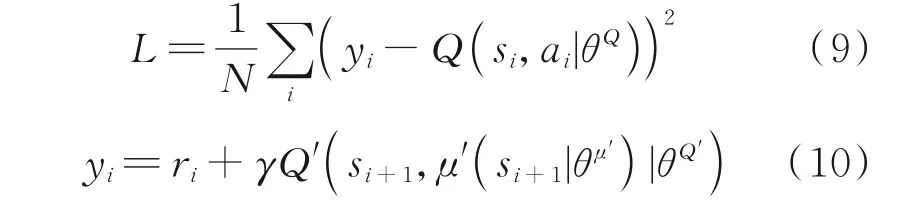
演员（actor）网络用于拟合确定性策略函数，该函数通过当前的状态选择合理的动作作为输出。对比评论家（critic），演员（actor）也有一个on⁃line 神经网络和一个target 神经网络，两个网络的参数θμ和θμ′的初始值相同。通过计算式（11）所示的策略梯度来更新online 策略网络的参数θμ。

式中τ一般取0.001。

2.2 环境状态设计

本文中强化学习agent 的动作空间维数为3，每一个动作包含3 个关节角的角速度θ̇2、θ̇3与θ̇4，即a=[θ̇2，θ̇3，θ̇4]。环境的状态需要实时反馈给agent，以便agent 根据这一反馈信息做出动作。结合1.1 和1.2 节的分析，环境状态设计如下：

（1）关节o、关节a、关节b和关节d相对于其零位的关节角分别为θ1、θ2、θ3与θ4；

（2）机械臂末端点g，虚拟目标物T′及虚拟障碍物M′ 在工作平面的位置分别为(xg，yg)、(xT′，yT′)和(xM′，yM′)；

（3）用于判断机械臂末端点g是否到达目标点范围的一个布尔变量为gt，若到达目标点范围，gt=1，否则gt=0。

式（5）已经给出机械臂末端点g的位置(xg，yg)，(xT′，yT′)与(xM′，yM′)分别为虚拟目标物T′与虚拟障碍物M′的位置。本文所设定的目标点在虚拟目标物T′上边界垂直向上10 mm 处（本文公式中所涉及的距离单位均为mm）。该目标点记为ξ，其在工作平面中的位置为(xξ，yξ)，其中xξ=xT′，yξ=yT′+10。利用机械臂末端点g与目标点ξ的距离dgξ来确定gt的值，dgξ的计算如式（13）所示。

2.3 碰撞检测与奖励函数设计

避障过程要求整个机械臂不能与障碍物发生碰撞，通过计算虚拟障碍物M′与机械臂在工作平面内的绝对距离来检测碰撞。

如图6 所示，当αaM′≤90°且αbM′≤90°时，直接计算虚拟障碍物M′与连杆ab的最小距离dabM′；当αaM′＞90°时，dabM′=|aM′|；当αbM′＞90°时，dabM′=|bM′|。dabM′按式（15）计算，αaM′与αbM′按式（16）计算。

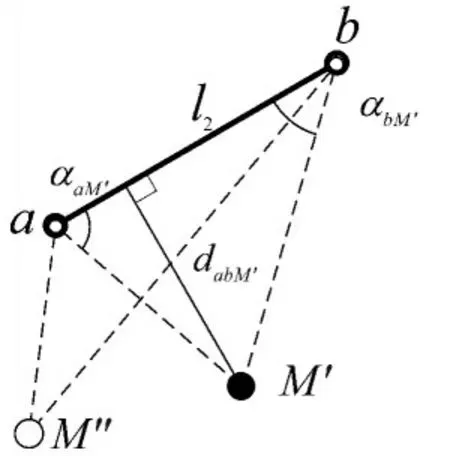
图6 碰撞检测Fig.6 Collision detection

连杆cd、ef与fg的碰撞检测亦如此处理，可分别得到dcdM′、defM′和dfgM′。在真实环境中，传统控制方法通过反复调试可以保证机械臂末端在跟踪目标物的同时不与目标物发生碰撞，而强化学习要求机械臂自己探索出目标跟踪路径，这可能使得机械臂在跟踪目标物的同时会与目标物发生碰撞。因此，本文添加了机械臂对虚拟目标物T′的碰撞检测。碰撞检测方法与上述方法相同，连杆ab、cd、ef与fg与目标物的距离分别为dabT′、dcdT′、defT′和dfgT′。最后，将min {dabM′，dcdM′，defM′，dfgM′}和min {dabT′，dcdT′，defT′，dfgT′}引入强化学习的奖励函数中，利用强化学习算法实现避障。

在强化学习中，奖励来自于环境，面对不同的任务，奖励函数需要根据任务特性和环境状态仔细设计［6］。仅考虑每回合机械臂末端点是否到达目标点范围所设计的奖励函数是一种稀疏奖励，但这样的奖励函数会使agent 很难获得奖励，算法收敛性差，导致模型学习缓慢甚至无法收敛。为此，本文设计了一种如式（17）所示的连续奖励函数R由此会导致机械臂脱离原有跟踪运动轨迹进行非必要的避障运动。针对该类问题，引入了如式（21）所示的避障纠正因子λ。其中，θΔ=|θ1-arctan(yM/xM)|为工作平面与障碍物所在平面的夹角。当θΔ＞θb时，λ无限接近于0 使得R3接近于0；而当θΔ＜θb时，λ开始激增，R3被激活以引导机械臂避开障碍物。θb为开启避障的阈值，与障碍物的尺寸、障碍物在空间中的位置及机械臂真实构型有关。R4用于引导机械臂避免与目标物T′发生碰撞，按式（22）计算。R5用于限制强化学习输出动作的大小，使得机械臂的运动轨迹更加平滑，按式（23）计算。

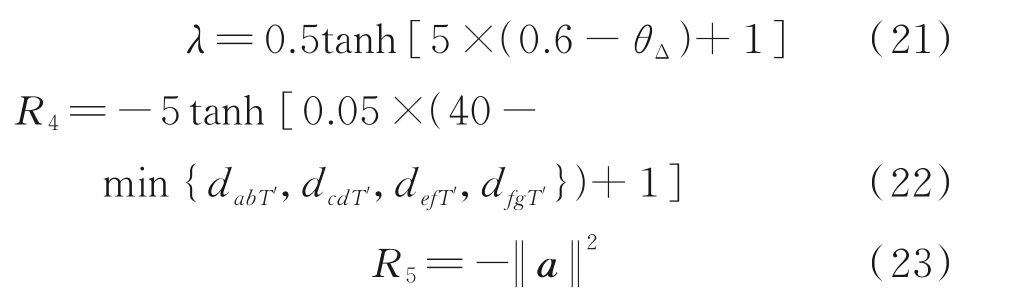
上述奖励函数R能够根据dgξ、min {dabM′，dcdM′，defM′，dfgM′}和min {dabT′，dcdT′，defT′，dfgT′}的大小来改变变化趋势，使得模型训练更加易于收敛，获得较好的学习效果。

3 动态目标跟踪与避障控制算法流程

R3用于引导机械臂避开虚拟障碍物M′，按式（20）计算。

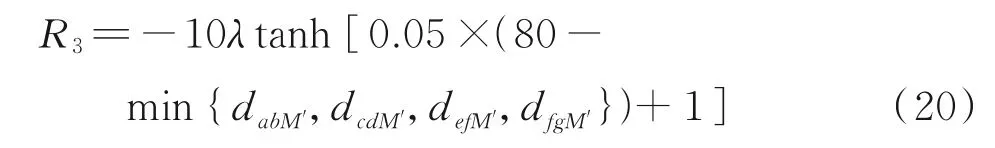
然而，仅按照上述方式可能会产生如下误判：在三维空间中障碍物并未与机械臂发生干涉，但基于其在工作平面的投影判定当前状态会发生碰撞，本文利用PID 控制方法控制机械臂的第一个关节（肩关节）o。PID 控制算法简单、鲁棒性好和可靠性高，经典PID 控制形式离散化表示为

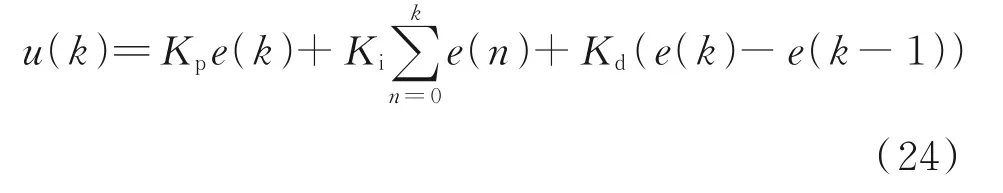
利用式（24），计算机械臂的工作平面（由关节o控制）与目标物的夹角作为误差e，利用误差反馈通过反复迭代尽可能减小夹角，最终使得机械臂的工作平面与目标物重合，从而将三维空间中机械臂的控制问题降维成二维平面机械臂的控制问题。动态目标跟踪与避障控制算法流程如下。

输入环境E，状态空间S，动作空间A。

初始化actor 和critic 的神经网络。

从初始回合后进入循环，第1 个Episode 时：

（1）初始化状态为s0。

（2）PID 控制。计算更新机械臂的工作平面和目标物的角度信息，计算角度的偏差值，通过PID 控制观测上一步的误差和累计误差来给出当前步的角度偏差，使得目标物与其在工作平面的投影重合。

（3）DDPG 控制。把st作为online 策略网络的输入，计算并加入噪声Nt得到动作

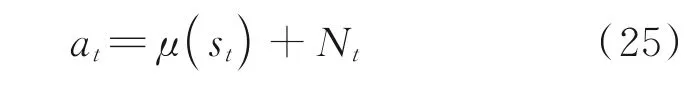
（4）执行当前动作at得到奖励rt和新的状态st+1，st+1作为下一步的状态值st=st+1。

（5）将样本(st，at，rt，st+1)存储到记忆库。

（6）记忆库达到一定的规模，从记忆库中采样N个样本N×(si，ai，ri，si+1)，开始学习。

（7）利用式（10）计算当前目标价值，通过式（9）更新onlineQ网络参数θQ。

（8）利用式（11）计算策略梯度，更新online 策略网络参数θμ。

（9）利用式（12）更新targetQ网络和target 策略网络的参数θQ′和θμ′。

（10）当达到最大步数时，则该轮训练结束，否则返回步骤2。

达到训练最大步数，第1 个Episode 结束，进入第2 个Episode 循环执行步骤1～10，直至Episode达到所设定的最大值，整个训练过程结束。

4 仿真校验

4.1 仿真参数设置

如表1 所示，仿真初始参数包含UR5 机械臂的初始状态、两种不同场景下目标物在空间中的初始位置、障碍物在空间中的位置。DDPG 算法参数和PID 算法参数分别如表2 和表3 所示，DDPG 算法参数按照一般情况选取，PID 参数经过反复调试所得。

表1 仿真初始参数Table 1 Initial simulation parameters

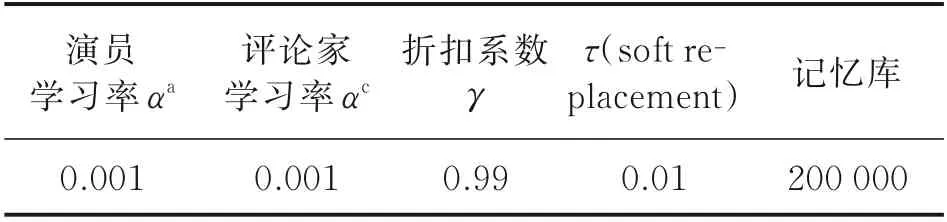
表2 DDPG 算法参数Table 2 Parameters of DDPG algorithm

表3 PID 参数Table 3 Parameters of PID

4.2 仿真结果

本文在MATLAB 环境下进行仿真测试。黄色正方体为障碍物，蓝色圆柱体为目标物。图7 和图8 为两种场景测试过程中机械臂状态变化。仿真测试分为两种场景，场景一为障碍物几乎不影响机械臂对目标物的跟踪；场景二为障碍物会严重影响机械臂对目标物的跟踪。

测试场景一机械臂状态变化如图7 所示，机械臂从初始位置出发，能迅速捕捉到目标物的位置并能够保持持续跟踪目标物。机械臂在跟踪目标物时会避免自身与障碍物发生碰撞。

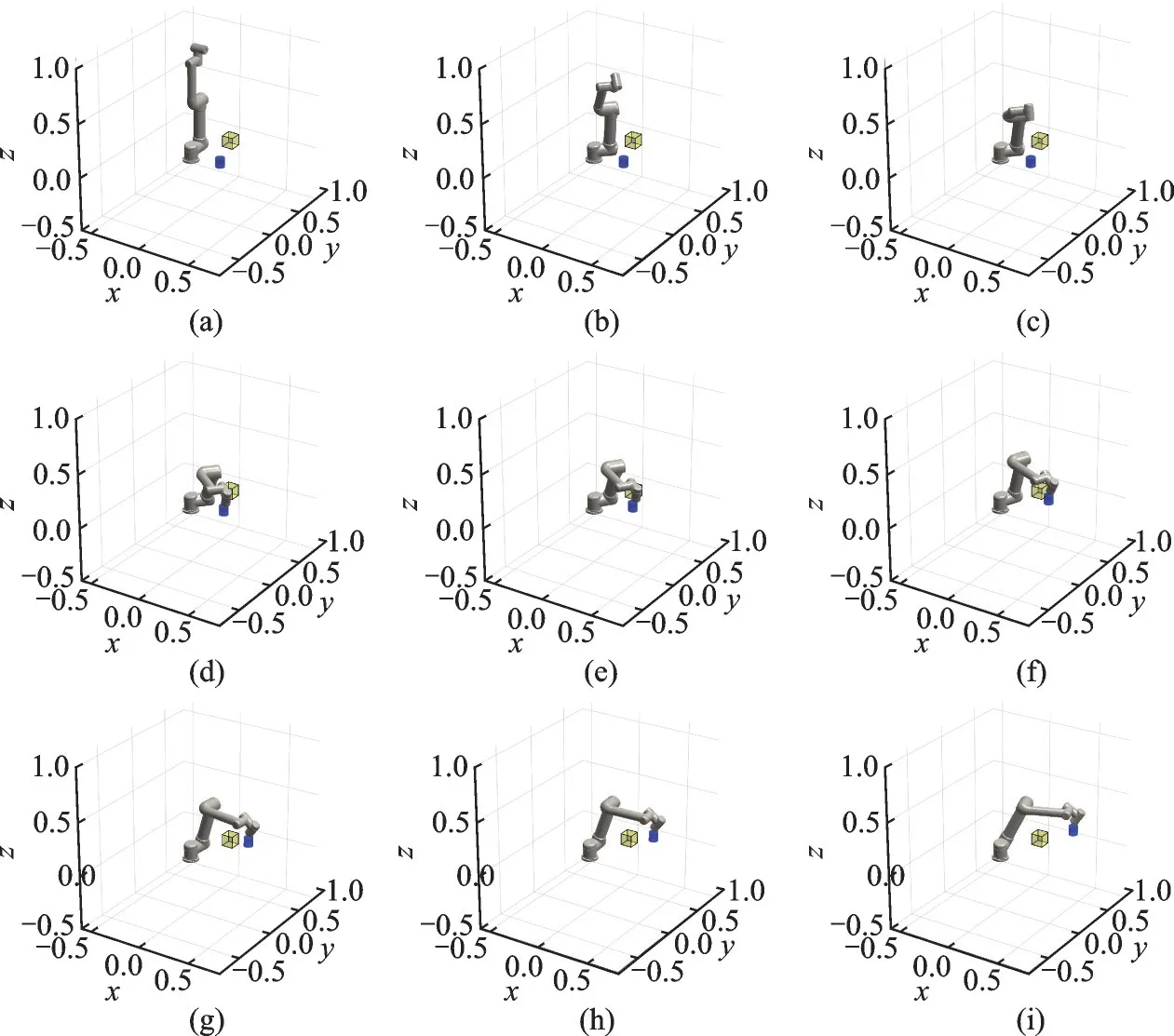
图7 测试场景一机械臂的状态变化Fig.7 State of the manipulator changes in scenario 1

测试场景二机械臂状态变化如图8 所示，此时障碍物对机械臂跟踪目标物的运动产生严重阻碍，机械臂会优先选择满足绕开障碍物的路径而远离了目标物，当障碍物对其轨迹不产生影响时会快速跟上目标物，这满足实际中避障优先的安全性原则。

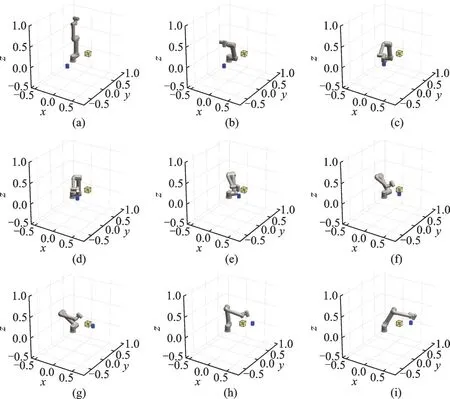
图8 测试场景二机械臂的状态变化Fig.8 State of the manipulator changes in scenario 2

为验证避障纠正因子λ的有效性，绘制了测试场景二机械臂典型状态在工作平面投影如图9（a）所示，对应三维空间中机械臂的状态如图9（b）所示。虽然工作平面内的障碍物投影与机械臂发生干涉，但由于纠正因子的作用未产生碰撞误判，实际三维空间中机械臂并没有产生无意义的避障运动，而是保持了原有的跟踪运动轨迹。

图9 测试场景二机械臂典型状态Fig.9 Typical state of the manipulator in scenario 2

此外，为验证所提DDPG⁃PID 控制方法的性能，直接将机械臂整体视为智能体，采用DDPG 算法来训练机械臂，将训练结果作为对比。图10（a）和图10（b）分别为本文所提出方法和仅使用DDPG 算法训练过程所获得的奖励情况。因为存在障碍物对机械臂的运动有阻碍和无阻碍两种不同场景，机械臂为避开障碍物而远离目标物从而导致奖励减小，所以奖励会有较大波动。DDPG⁃PID方法不仅能够获得更高的奖励，而且收敛性要比仅使用DDPG 算法好，前者奖励在后期能较为稳定地收敛并获得1 000 上下浮动的奖励，机械臂能够获得较为理想的自主跟踪目标与避障的能力；后者奖励在后期出现下降的趋势，机械臂自主决策能力（目标跟踪与避障）不足。这表明，DDPG⁃PID 控制能够有效确保机械臂的控制效果，实现对目标稳定跟踪的同时避开障碍物。

图10 训练过程的奖励情况Fig.10 Reward during training

5 结论

本文将传统PID 控制和DDPG 强化学习结合，提出了DDPG⁃PID 控制方法控制机械臂在动态复杂环境下实现对目标的稳定跟踪和避障。引入PID 控制使得算法收敛效果和控制性能更好。关节偏置的引入使得模型更加贴合实际机械臂的构型，而避障纠正因子的引入成功解决了投影法会造成机械臂对碰撞误判的问题。本文后续将针对机械臂对动态目标的跟踪精度问题以及机械臂操作环境存在动态障碍物的情况，结合模型预测控制进行进一步研究。