基于机会约束的电厂混煤煤质和成本的Pareto前沿
2022-03-17刘福国刘科王守恩
刘福国,刘科,王守恩
(1. 国网山东省电力公司电力科学研究院,山东省 济南市 250002;2. 山东电力研究院,山东省 济南市 250002)
0 引言
火力发电机组在设计上燃用特定煤种,因为市场供应变化,或为降低燃料成本,发电用煤常常采用2 种以上不同品质的煤种掺配而成。煤种改变对机组运行影响较大,合理掺配不仅能够减少掺烧对锅炉和辅助设备带来的危害,而且有利于控制二氧化硫排放,降低电厂运行成本[1-2]。
为控制混煤煤质,文献[2]给出了不同掺配模型,这些模型基于煤成分的可加性,将混煤成分表示成掺配原煤成分的加权平均值。在保证混煤煤质满足一定要求的前提下,线性规划模型[3]可确定不同原煤的掺混量,以实现产量最大或成本最低。
线性规划模型通常认为掺配原煤具有确定的成分,而实际上,即使来自同一矿点的原煤,其成分也是变化的[4]。具有确定性约束的线性规划模型无法处理掺配煤种成分的波动,而机会约束规划(chance constrained programming,CCP)[5]将掺配煤种成分作为随机变量,控制混煤成分落入某一范围的概率,而不是保证这些成分在确定范围内,这更符合实际掺配状况。机会约束规划对混煤煤质不确定性更具鲁棒性[5-6]。
可靠实用的掺配规划模型不仅要控制混煤煤质,并保证效益最大化,还要考虑掺配设备调度和掺配场地约束,此时线性规划模型和混合整数模型相结合,在时间框架下对掺配过程进行动态优化[4-5]。
混煤掺配通常在煤矿(生产商)[7]、洗煤厂(中间商)[8]或发电厂(用户)等[9]不同场所进行,采用的规划模型也有一定差别。对于煤矿和洗煤厂,在保证满足用户合同煤质的前提下,优化目标是最大限度地提高产量。而对于发电厂,优化目标通常是保证单位质量的混煤成本最低[3-4]:

式中Pi和xi分别为第i个掺配煤种的价格和份额。
电厂生产目的是发电,发热量是煤发电能力的重要指标。式(1)以单位质量原煤成本作为优化目标,未考虑发热量对发电能力的影响,因而欠合理。与通常的线性规划模型不同,文献[10]以混煤成本作为优化目标时,考虑了机组燃煤量、煤发热量与发电量之间的关系,因此,更接近电力生产实际;但建立这三者之间的关系较为困难,通常需要进行大量试验工作。
线性规划模型采用如下约束条件[3-4,10]对混煤煤质进行控制:

式中:Bi为第i个掺配煤种的某种成分;B1和B0分别为混煤中该成分的控制上限和下限。
以式(2)作为约束条件、按式(1)给出的目标进行寻优,得到的优化结果通常指向式(2)的上、下边界点。比如,对于灰成分,寻优结果通常接近式(2)的上边界B1。这是因为灰分大的煤,其价格通常较低,易于达成成本目标。因此,以混煤成分作为约束条件的规划模型,能够将成分控制在一定范围内,但并未进行混煤煤质优化。尽管文献[11]提出一种以混煤煤质作为优化目标的掺配模型,并采用权重系数来平衡不同成分的重要性,但未能给出权重系数的选取原则。因此,混煤掺配时,不应过度考虑混煤成本,应权衡煤质及其带来的影响[1]。
煤由固定碳、挥发分、水分、灰分和硫分等多种成分组成,虽然不同成分的重要性因锅炉而异,但每种成分都有独特的影响方式和范围,它们共同决定了煤的燃烧特性。一般来说,机组对设计煤有最好的适应性,基于此,本文定义了锅炉设计煤的最大似然煤质,它是掺配条件下与设计煤最相似的煤质。以最大似然煤质和单位发热量的成本作为优化目标,提出电厂混煤掺配多目标机会约束优化模型,并给出该问题的Pareto 前沿解。
1 优化目标
1.1 原煤成分和发热量分布特性
电厂混煤通常采用2 个或多个矿点原煤掺配而成。本研究追踪了多个矿点供给电厂的原煤工业分析数据,对不同矿点原煤的成分和发热量进行分析,发现即使是同一矿点原煤,不同时间采集煤样的成分和发热量也是变化的,且变化幅度远超出测量误差范围,因此,可以确定这种变化是由煤质波动引起的。
虽然矿点原煤的成分和发热量是波动的,但对于同一矿点,开采煤层稳定时,原煤成分和发热量通常符合一致的统计规律。图1 是进入电厂的某矿点原煤的固定碳、灰分质量分数以及发热量的概率密度分布,包含1 256个样本数据,图中红线是以样本数据均值μ和标准差σ作为分布参数的正态分布概率密度,可以看出,原煤成分和发热量基本服从正态分布。

图1 某矿点煤成分和发热量概率密度分布Fig.1 Probability density distribution of coal comp osition and calorific value in a mine
因此,在电厂进行煤掺配时,将掺配原煤成分和发热量作为确定数据,不符合掺配煤种的实际状况。本文提出的掺配模型将掺配煤种成分和发热量作为随机变量,并假设它们服从正态分布。
1.2 设计煤的最大似然煤质
煤质采用工业分析表示,主要包括水分质量分数φM、灰分质量分数φA、挥发分质量分数φV、固定碳质量分数φFC、全硫分质量分数φS和发热量Q,记为

式中ωi为Ω中第i个工业分析数据,如ω2表示灰分质量分数φA。
对于机组设计煤,用下标“0”区分,记为
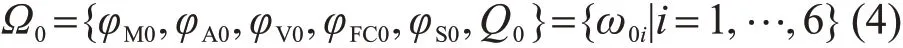
假设混煤由N个煤种掺配而成,第j个煤种的第i个工业分析数据记为ωij,第j个煤种的掺配份额为xj。根据煤成分的可加性,得到混煤第i个工业分析数据ωHi为

要使L达到最大,需使-lnL达到最小。因此,在进行煤掺配时,混煤煤质的优化目标是设计煤最大似然煤质,即式(12)中p1达到最小时的混煤煤质。
1.3 单位发热量的成本
发热量是煤发电能力的重要指标。文献[4]给出的掺配模型是以“1 t混煤成本最低”作为优化目标,忽略了混煤发热量的影响,而本文中提出的掺配模型是以“单位发热量成本最低”作为优化目标。
单位混煤发热量的成本定义为H6

混煤成本优化目标就是使E(p2)达到最小。与式(1)相比,式(15)表示的优化目标是非线性的。
2 约束方程
2.1 掺配份额直接约束
根据式(12)和(15)对混煤煤质和成本进行优化,寻找最大似然煤质和最小成本。优化时还要对掺配煤种份额进行约束,最常见的是掺配份额完整性约束,即

煤的结焦性是掺配时要考虑的重要因素,现场控制混煤结焦的最实用方法是使易结焦原煤掺配份额xj小于某个给定值u,即

u的值通常根据试验确定。
当某个掺配煤种因市场因素购买数量较多,掺配时必须保证该煤种掺配份额xj大于某一给定值l,即

虽然煤具有多种成分和性质,但对于特定机组,某些成分或性质可能对机组影响更为显著,如煤水分是影响某1 000 MW 机组出力的首要因素[9]。因此,有时还需要对混煤的某些成分或性质单独进行附加约束。
根据式(5),混煤工业分析成分ωHi是随机变量,对于这类变量,无法直接给出确定性约束,对这类随机变量的约束只能是保证它落入某一范围的概率。
2.2 硫、灰分和水分质量分数机会约束
要控制混煤硫质量分数ωH5小于某一给定值S*的概率大于α,即

因此,已知式(20)中α和S*,将α代入式(23)中得到S′,只要S′满足式(24),式(20)就成立。因此,式(24)将式(20)所表示的机会约束转换成了确定性约束。
与硫质量分数ωH5相似,混煤灰分质量分数ωH2和水分质量分数ωH1也常常采用式(20)所表示的机会约束。
2.3 挥发分、固定碳质量分数和发热量机会约束
要控制混煤挥发分质量分数ωH3大于某一给定值V*的概率大于α,即

式中μH3和σH3分别按式(8)、(9)计算。
根据式(26),挥发分质量分数随机变量ωH3的累积分布函数为

因此,已知式(25)中α和V*,将1-α代入式(28)得到V′,若V′满足式(29),式(25)即成立。因此,式(29)将式(25)所表示的机会约束转换成了确定性约束。
与挥发分质量分数ωH3相似,混煤固定碳质量分数ωH4和发热量ωH6也常常采用式(25)所示的机会约束。
3 掺配优化模型及分析
3.1 掺配原煤和设计煤种
以某发电机组为例,该机组发电用煤由3 种原煤掺配而成。3 种原煤的工业分析成分分布参数和煤种价格作为已知条件,表1 为式(6)中的μij和σij,以及式(13)中的Pj等数据取值。

表1 掺配煤种的工业分析参数分布及价格Tab.1 Proximate analysis parameter distribution and price of blended coal
锅炉设计煤水分质量分数ω01=8.0%,灰分质量分数ω02=25.86%,挥发分质量分数ω03=27.95%,固定碳质量分数ω04=43.71%,硫分质量分数ω05=0.64%,收到基低位发热量ω06=21 271 kJ/kg。
3.2 多目标掺配优化及Pareto前沿
选择设计煤的最大似然煤质p1、成本的数学期望E(p2)作为优化目标,进行煤质和成本的多目标寻优,式(17)—(19)、(24)、(29)是多目标优化的约束条件,其中式(17)是必选约束条件,其余为可选约束条件。
入炉煤质波动大,使运行参数调整难度增加,给机组安全运行带来隐患,因此,有研究[2,8]认为,煤质的稳定性和实际煤质同等重要。式(9)中的标准差σHi反映了该成分的稳定性,σHi越小,该成分越稳定。其中,混煤发热量标准差σH6是反映煤质稳定性的最重要参数。因此,在上述煤质和成本的2 个优化目标的掺配模型中,可补充发热量标准差σH6作为第3个优化目标,寻找使σH6较小,即煤质较稳定的掺配方案。
根据机组运行特性和掺配原煤的实际状况,选择不同优化目标和约束条件,组成不同的掺配优化模型,见表2。
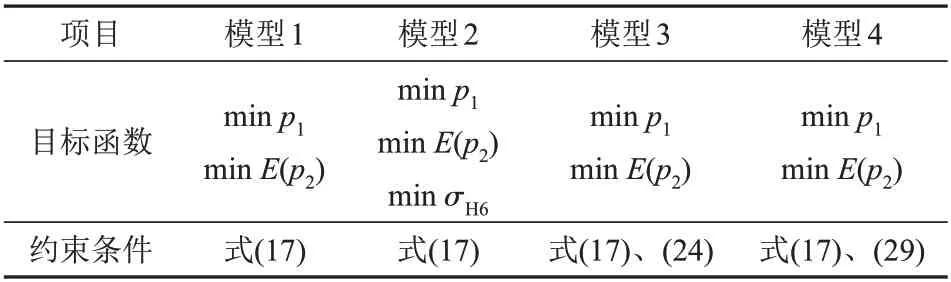
表2 掺配模型Tab.2 Blending model
多目标优化问题有多种求解方法[15]。对于上述多目标优化问题,采用具有强大搜索能力的遗传算法,找出决策者所需的所有可能的优化解,也称为Pareto前沿。
多目标优化计算采用MATLAB 软件,利用gamultiobj 函数进行遗传算法多目标寻优。采用norminv 函数计算式(23)、(28)中的反函数φ-1S(α)、φ-1V(1-α)。
3.3 分析和讨论
模型1、3、4 是关于煤质和成本的2 个目标优化,模型2 是关于煤质、成本和发热量标准差σH6的3 个目标优化。其中,模型1、2 未对单个成分进行约束。模型3 对含硫量进行约束,见式(24),其中S*=0.8%,α=0.95,表示混煤中硫质量分数ωH5小于0.8%的概率大于0.95。模型4 对挥发分进行约束,见式(29),其中V*=25%,α=0.8,表示混煤中挥发分质量分数ωH3大于25%的概率大于0.8。
模型1 煤质和成本的Pareto 前沿见图2,图中还给出了一些随机选取的煤质-成本分布点。可以看出,对于Pareto前沿中的任何一个解,该解的2个优化目标都不比Pareto 前沿解集外的点差,且至少有一个目标比解集外的点好。

图2 2个目标的Pareto前沿Fig.2 Pareto fronts of two goals
对于模型2,煤质-成本-发热量标准差的Pareto 前沿见图3,Pareto 前沿在分布点中的位置特点与模型1相同。在模型2的Pareto前沿中,发热量Q标准差σH6=722~1 365 kJ/kg;而对于Pareto前沿之外的点,σH6=722~1 841 kJ/kg。可见,Pareto前沿解的发热量波动明显减小,这是因为与模型1相比,模型2增加σH6作为优化目标。模型2的Pareto前沿的煤质和成本目标相较于模型1稍有降低:对于模型1,成本E(p2)=15.3~20.7 元/MJ,煤质p1=26.39~26.98;而对于模型2,E(p2)=15.3~21.9元/MJ,煤质p1=26.33~27.34。

图3 3个目标的Pareto前沿Fig.3 Pareto fronts of three goals
模型3 增加了混煤含硫量的机会约束。从模型3的Pareto前沿中任取一个优化解,该优化解所对应的混煤含硫量ωH5服从式(7)所示的正态分布,ωH5的概率密度分布见图4,阴影部分表示硫质量分数小于0.8%的概率,该概率值大于0.95。

图4 混煤含硫量概率密度分布特性Fig.4 Probability distribution characteristics of sulfur content in blended coal
模型4的Pareto前沿中一部分优化解的信息见表3,包括掺配份额xj、p1、E(p2)以及混煤工业成分ωHi等。ωHi服从式(7)所示正态分布,其数学期望μHi和标准差σHi也在表3中给出。可以看出,混煤成分、发热量与设计煤较为接近。
表3 中优化解按照x1从小到大排序,可以看出,随着x1的增大,煤质目标p1逐渐减小,成本目标E(p2)逐渐增大。因此,当成本目标的权衡较大时,应选择x1较小的解;当煤质目标的权衡较大时,应选择x1较大的解。由于实例机组的煤种适应性较好,因此,推荐选择x1较小的优化解,如第1个优化解。从表3还可以看出,x1越小,所对应的发热量标准差σH6越小,这意味着煤质波动性越小,有利于机组稳定运行。
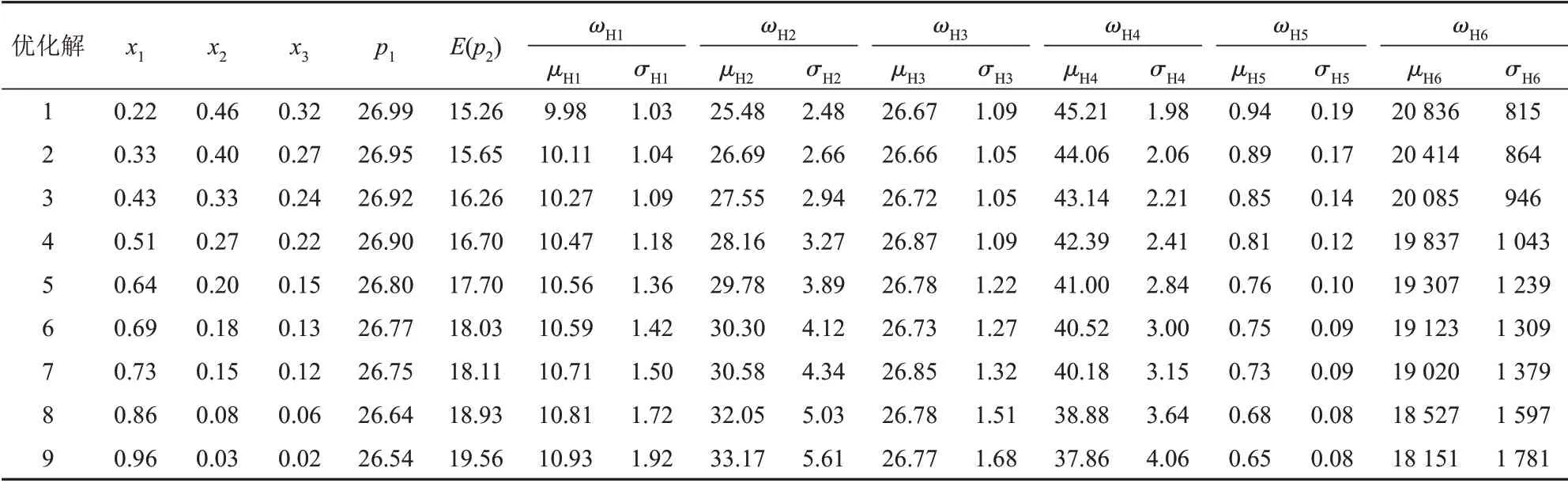
表3 Pareto前沿中一部分优化解Tab.3 Some optimal solutions in Pareto fronts
对于第6 组优化解中的混煤挥发分质量分数ωH3,其概率密度分布见图5,图中阴影部分表示挥发分质量分数大于25%的概率,该概率值大于0.8。

图5 混煤挥发分概率密度分布特性Fig.5 Probability distribution characteristics of volatile matter in blended coal
由于表1 给出的3 个掺配原煤灰熔点均较高,不易结焦,因此,不需要选择式(18)作为掺配模型的约束条件。当掺配煤种灰熔点较低时,可增加式(18)作为模型的约束条件。
4 结论
定义了锅炉设计煤种的最大似然煤质,以最大似然煤质和单位发热量的成本作为优化目标,建立了电厂混煤掺配多目标机会约束优化模型,并给出该模型的Pareto前沿解。具体结论如下:
1)即使是同一矿点的原煤,其成分和发热量也是变化的,变化幅度远大于测量误差范围,这种变化是由煤质的波动引起的。因此,电厂混煤掺配时,将掺配原煤的成分和性质视为随机变量,更符合实际状态,更具鲁棒性。
2)对于所建立的基于机会约束的电厂混煤煤质、成本以及煤质稳定性的多目标优化模型,采用遗传算法可得到煤质和成本多目标优化问题的Pareto 前沿。一台实际运行机组的掺配优化示例表明,所得煤质和成本数据合理,结果满足机会约束要求。
