基于类噪声数据的电力系统低频振荡模态参数辨识
2022-03-17闫红艳HwangJinKwon高艳丰
闫红艳,Hwang Jin Kwon,高艳丰
(1. 河北工程大学水利水电学院,河北省 邯郸市 056038;2. 韩国又石大学能源工程系,韩国镇 川365-803)
0 引言
随着电网远距离、大容量输电的实施,高放大倍数励磁装置的使用以及大规模新能源的接入,低频振荡时有发生,频率范围一般为0.1~2.5 Hz[1],严重危害到系统正常运行。低频振荡模态识别是分析低频振荡产生原因的基础,也是实现电力系统实时高效控制和风险预警的关键之一[2-5]。
基于相量测量单元(phasor measurement unit,PMU) 的电力系统广域测量系统(wide area monitoring systems,WAMS)能够实时地记录电力系统的动态行为,按照量测信号的辨识方法可分为基于大扰动后自由振荡响应信号的方法和基于环境激励下随机响应信号的方法[6-10]。大扰动数据包含强低频振荡分量,能够准确识别区域间模式,但这类事件很少发生,很难进行连续的模态识别。相反,负荷随机波动引起的小扰动激励(又称类噪声数据)时刻存在、易于采集、数据丰富,可及时准确地反映当前系统的运行特性[11]。Prony 算法及其改进算法在分析大扰动激励下的响应信号应用较广泛,但Prony 算法在处理噪声信号和具有时变特性非平稳信号的能力不理想[12-13]。基于环境激励下随机响应信号的方法大多在信号的自回归(auto regressive,AR)模型[10]或自回归滑动平均(auto regressive moving average,ARMA)模型上发展起来的[14-16]。文献[17-18]采用最小二乘法求取电力系统随机响应信号AR 模型的最优参数,进而获得低频振荡的频率和阻尼比信息,但是该算法存在数值不稳定的问题。文献[19]提出了用Yule-Walker 方程解AR 模型的功率谱分析方法;文献[20]提出了一种基于数学形态学自回归移动平均(mathematical morphology,MM-ARMA)算法的辨识方法。文献[21]釆用Bootstrap 法确定YW 法辨识结果的置信区间。改进扩展的Yule-Walker(modified extended Yule-Walker,MEYW)方法[22]广泛用于基于环境数据自相关函数的AR 模型中,但AR 模型的阶数较难确定,存在2 个频率相近的振荡模式无法区分辨识的现象。
随机子空间方法(stochastic subspace identification,SSI)从原理上既适用于自由振荡信号分析,也适用于由环境激励引起的系统随机响应信号分析,抗噪性强,模态识别结果较准确,但计算速度较慢,很难反映信号的时变特性[7,23]。低频振荡产生的直流分量会降低模态识别的准确性,上述方法在使用过程中数据均需进行去除直流预处理。希尔伯特-黄变换(Hilbert-Huang transform,HHT)算法是分析非线性、非平稳功率振荡的常用工具,虽然能分解出直流分量,但存在端点效应现象[24]和本征模函数筛选效果不理想等固有缺点,辨识结果误差率较大。文献[25]提出集合经验模态分解(ensemble empirical mode decomposition,EEMD)算法,但该算法存在计算复杂、耗时长等问题。
变分模态分解(variational mode decomposition,VMD)是一种新的非递归的信号分解方法,除了能滤除直流外,还能克服经验模态分解(empirical mode decomposition,EMD)和EEMD 方法的缺陷,噪声鲁棒性较好。本文采用基于模态相关系数的VMD 进行类噪声数据处理,直接去除中心频率为0 的直流部分并分离出低频振荡信号;低频振荡信号模态参数辨识利用信号频率差序列的自相关函数表示为与低频振荡函数形式一样的指数衰减正弦函数的线性组合,该函数的固有频率和阻尼比等于振荡模态的固有频率和阻尼比,用不同时间频率数据之间的差序列减少测量噪声的影响。通过在频域中峰值频率附近的离散傅里叶变换(discrete Fourier transform,DFT)进行曲线拟合来估计其拉普拉斯变换系数,然后计算得出模态分量的参数。通过与MEYW方法的识别结果相比较,验证了所提识别方法的准确性。最后,采用基于ARMA 模型产生PMU 频率数据和某实际系统的实测频率数据验证方法的可行性和有效性。
1 改进的变分模态分解方法
1.1 VMD原理
VMD 是Dragomiretskiy 提出的非递归信号分解方法,实质是变分问题,根据预设模态分量个数对信号进行分解[26]。该方法通过一个自适应维纳滤波器组将原始信号f(x)分解为K个中心频率为ωk的模态函数uk,其中K为预设模态分量个数。VMD算法在抗噪声和非平稳信号处理方面具有较好的性能和较高的运算效率,可以分解出直流分量。
为了得到具有一定带宽频率的K个模态分量,通常对每个模态函数uk进行Hilbert 变换得到边际谱:
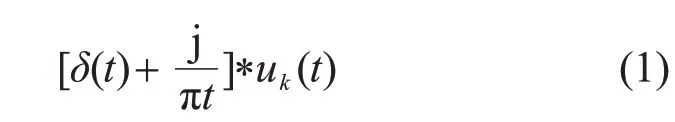
式中:δ(t)为狄利克雷函数;j2=-1;*为卷积符号。预估各模态解析信号中心频率,将每个模态的频谱调制到相应的基频带:

式中:{uk}={u1,…,uK}为分解得到的K个模态分量;{ωk}={ω1,…,ωK}为各分量的频率中心。
受约束的变分问题求解,可引入二次惩罚因子α和拉格朗日乘法算子λ(t),得到增广拉格朗日公式:

利用乘法算子交替方向法求取式(6)变分问题,通过交替更新un+1k、ωn+1k和λn+1寻求增广拉格朗日表达式的鞍点。式(5)为约束变分模型的最优解,从而将f分解为K个窄带IMF 分量。VMD 算法的具体过程如下:
1)初始化{u1k},{ω1k},λ^1,n=0;
2)n=n+1,执行迭代循环;
3)使k=k+1,按照式(5)与式(6)更新u^n+1k与ωn+1k,直至k=K;
4)按照式(7)更新λ^n+1;

1.2 基于相关系数的模态个数设定
VMD 本身不具有自适应性,模态分解数K值的设置是信号VMD 分解的关键环节,对分解效果影响较大。K设定值大于待分解信号所含的固有模态(intrinsic mode function,IMF)分量个数,则会在最终结果中引入虚假模态分量,影响对原始低频振荡信号的分析;相反,K设定值过小,则将导致信号分解不完全,即振荡信号中含有的重要模态没有被完全分解出来。
本文利用模态分量的相关系数来确定VMD分解个数的方法。首先取K值为2,计算各个分量之间的相关系数,判断各分量之间是否存在频率混叠现象,自适应确定模态个数。分量x1(n)和分量x2(n)的相关系数定义为

基于模态相关系数的VMD 算法具体步骤如下:
1)初始化K= 2,并用VMD 算法处理原始信号;
2)计算各个模态分量之间的相关系数,提取其中最大的相关系数;
3)K→K+1,并根据步骤2)更新模态之间的最大相关系数;
4)重复步骤3),直到最大相关系数超过阈值。经过大量实验分析,最大相关系数的阈值选取0.1较为合适[27]。
根据文献[26],当惩罚参数α=2 000时,它可以满足大多数工作条件的实际需求。试验表明,改变α时影响很小,因此取默认值,当存在直流分量时,DC=1,这意味着可以分解出中心频率为0 的分量。本文首要任务是要滤除直流分量,所以DC取1,其余参数取默认值。
2 电网区域间低频振荡模态辨识
2.1 类噪声数据的ARMA模型
负荷的随机变化即使很小也会影响到供需之间的不平衡,通常将这种干扰看作高斯白噪声[28],在电力系统类噪声数据中用直流分量d(t)和低频振荡模式s(t)表示。同时,考虑到WAMS 数据中含有各种测量噪声w(t),因此,电力系统正常运行时,PMU数据的信号模型可表示为

式中:J为系统的惯性常数;f0为标称频率;Ks为系统的功率/频率特性;u(t)为系统负载功率缺额的标幺值。d˙(t)是频率波动引起的直流分量,即每日负荷波动时的功率缺额;u(t)是阶跃函数的总和,是负荷切换时间的函数[30]。日常负荷随机变化被建模为环境频率数据中的白噪声,所以d(t)以白噪声v(t)为输入时表示为
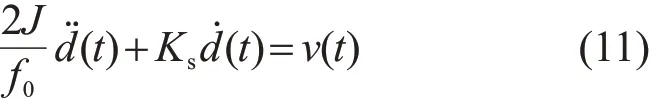
式中v(t)=-u˙(t),随着v(t)的强度变强,由于电力系统中的调速器或频率控制,随着时间的推移,v(t)的强度可能会逐渐不同于其实际值。
扰动v(t)引起电力系统频率中的低频振荡s(t)。振荡模式被表示为二阶微分方程[31]。K个振荡信号可表示为

式中:w[n]是测量噪声;d[n]=d(nTs);s[n]=s(nTs),Ts是PMU 的采样周期。测量噪声w[n]可以看成白色高斯信号,其均值和方差分别是0和σ2。y[n]的信噪比(signal noise ratio,SNR)定义为s[n]与w[n]的功率比。在模拟产生数据和模态识别时,可将式(11)和式(13)的连续时间方程转换为离散时间方程,用脉冲响应不变法[32]进行转换,表示成ARMA模型为:

2.2 模态参数辨识
将原始频率信号y[n]进行VMD分解,分离出中心频率为零的直流分量d[n],同时得到K-1个有限带宽的固有本征模分量,根据其频率值可直接提取出含噪声的低频振荡分量sw[n],再对该模态分量进行参数辨识即可得系统的振荡参数。含噪的低频振荡信号sw[n]的ARMA模型可以表示为
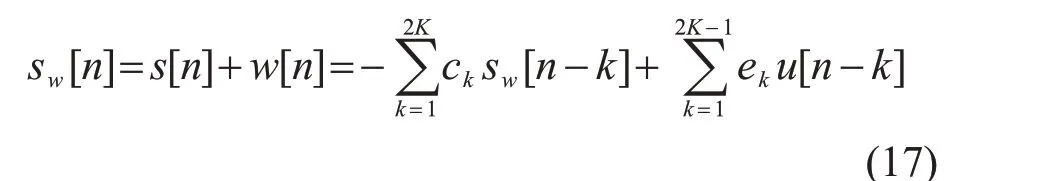
式中ck和ek分别为自回归部分和滑动平均部分模型参数。
由信号的自相关特性可知,自相关分析能有效消除信号中的噪声,且能保留原信号函数的频率特征[33-34],随着时间的延长,噪声信号自相关函数值将很快衰减至0,因此,可以采用自相关函数代替原函数进行模态辨识。
故sw[n]的自相关函数可以表示为

rw[m]是与式(17)中的AR模型具有相同特征多项式的线性预测模型[34]。因此,rw[m]的连续信号也可以表示为K个指数衰减正弦分量的线性组合,表达式为

式中Re{·}代表复数的实数部分。
2.3 频域的曲线拟合过程
公式(19)自相关函数rw[m]进行DFT的结果为

为了减少曲线拟合中的噪声影响和缩短计算时间,希望在fk附近使用Rw[m],fk是低频振荡模态功率最集中的地方。最好在以下频率范围上进行曲线拟合:|f^k-f|≤fc,k=1,2,…,K。
本文中将fc设为0.05 Hz,其宽度足以包含每个峰值的频率范围。每一个峰值曲线拟合采样的最大整数小于2fc/△f。角频率采样点表示为ωk,m和ωk,(m+1)=ωk,m+2π△f。m=1,2,…,M是第K个模态峰值的曲线拟合。
信号VMD 分解后,取低频振荡频率范围内IMF分量,并对此分量做自相关计算,按式(24)中R(s)的系数ak和bk来辨识模式信号各参数的值。整个过程通过将R(s)拟合到频域中的R[m]中来实现。R(s)在频域中可以表示为


式中†表示伪逆,X的解即式(24)的系数ak和bk。则第k个模态参数f^k,ζ^k,A^k和φ^k即可通过式(24)和式(25)计算得出。再由式(20)可得r[n]的拟合值r^[n]:
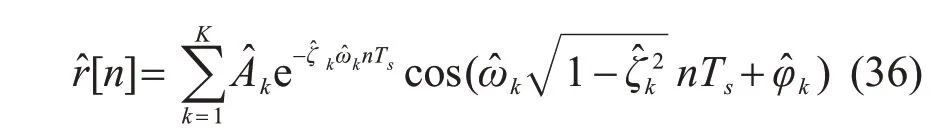
2.4 结果评价
信号拟合曲线与原信号越接近,辨识结果精确度也越高。拟合精度采用信噪比SNRe为指标,单位为dB。
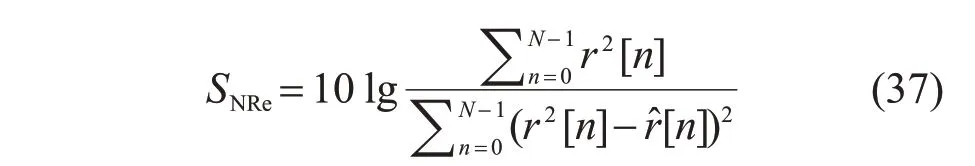
式中:r[n]为测量信号;r^[n]为曲线拟合重构信号;SNRe的结果越大,表示拟合信号与原始信号拟合的效果越好。
本文采用VMD分解滤除原始数据中的直流分量,并提取出系统低频振荡信号,然后做自相关计算消除噪声,低频振荡参数由自相关函数的拉普拉斯变换计算得到,而拉普拉斯变换式(22)的系数通过信号自相关函数DFT的曲线拟合来估计,最后由ARMA模型产生的类似真实PMU的频率数据和实测PMU频率数据验证方法的有效性和准确性。
3 实例分析
3.1 模拟数据算例分析
由式(9)可知,PMU数据由3部分组成,为了验证所提方法的可行性和有效性,利用式(15)和式(16)的ARMA模型模拟产生PMU频率数据进行验证。由ARMA模型可通过程序模拟产生离散的PMU数据,直流分量[27]取值如表1所示,2个低频振荡分量取值如表2 所示。模拟采样时间间隔为0.02 s,加入不同信噪比的高斯白噪声来模拟测量噪声。

表1 模拟直流分量的参数Tab.1 Parameters of the analog DC component

表2 低频振荡分量的参数Tab.2 Parameters of low-frequency oscillation components
模拟数据测量噪声信噪比取30 dB 高斯白噪声时,对模拟数据先经过低通滤波处理,低通滤波是基于高速采样频率50 Hz设计的2阶巴特沃兹低通滤波器,截止频率为5 Hz,滤除高频分量可减少VMD 分解个数,增加运行速度。采用相关系数的VMD算法确定分量个数K,分量之间的最大相关系数如表3所示。由表3可知,当K取4、5时,信号经VMD算法分解之后分量之间的最大相关系数均大于阈值0.1;而当k取2、3时,最大相关系数皆小于阈值0.1。故取K值为3,VMD分解结果如图1所示。

表3 不同K值的最大相关系数Tab.3 Maximum correlation coefficients of K different values
由图1可知,信号经VMD分解后的各个IMF呈现比较规范,彼此间没有模态混叠现象,各个频段分离效果较好。其中IMF0是中心频率为0的直流分量,其余的是不同频率范围的主导振荡频率,为后续准确辨识出低频振荡特征参数提取提供了理想的模态分量。
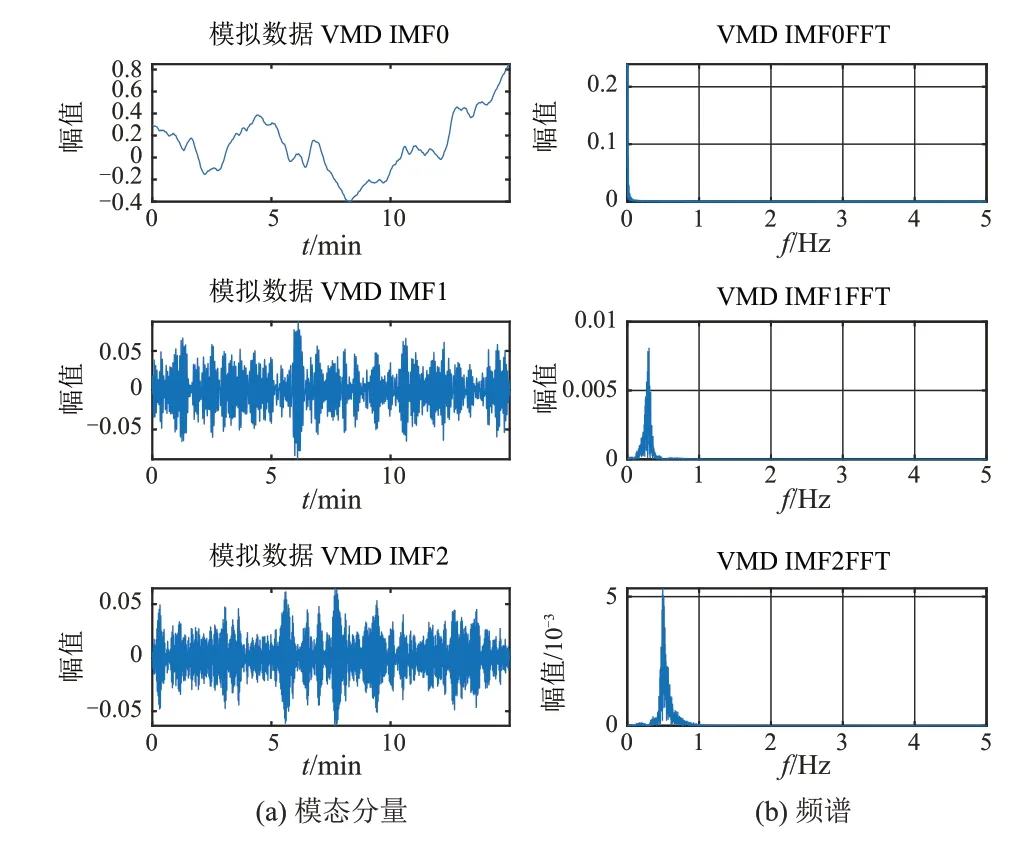
图1 VMD模态分量及频谱Fig.1 The spectrum and VMD modal component
与EEMD算法相比,VMD算法具有较好的优越性,EEMD 分解结果如图2 所示。从图中可以看出,经过EEMD分解后得到13个IMF,右侧为对应频谱。分解得到的模态个数远远多于原始信号含有的振荡分量个数,且耗时很长,同时出现了模态混叠,无法准确反映原始信号的低频振荡分量,严重影响参数提取的准确度。
以图1 中IMF1 和IMF2 信号为例进行分析,对IMF1 分别利用频差序列DFT 的曲线拟合法和MEYW法进行振荡分量模态辨识,辨识算法采样频率为50 Hz,自相关函数的有效持续时间设置为20 s,数据窗长为5 min,相邻数据窗间隔为1 min,数据总长为15 min。得到3~8 min 的频率偏差波形和20 s频率偏差的自相关拟合曲线如图3所示,拟合DFT 幅值和角度如图4 所示。可以看出拟合曲线非常接近辨识信号的曲线,辨识结果准确度高。图5给出IMF1分量的频率和阻尼比的辨识结果,从图中可以看出2 个方法的频率偏差比较小,基于MEYW法的阻尼率值偏小,且受噪声影响某个时间段误差会比较大,而基于DFT的曲线拟合法变化比较平稳,抗噪性好。将各滑动窗口内辨识得到的模态参数取平均值得到辨识结果。采用同样的方法,将测量噪声设成10 dB 高斯白噪声时,K值为4,并对低频振荡频率范围内的分量进行模态辨识,模拟数据辨识结果如表4所示。

图3 模拟数据IMF1分量的频率偏差波形及自相关函数Fig.3 Frequency deviation waveform and autocorrelation function of IMF1

图4 模拟数据IMF1分量的DFT幅值和角度Fig.4 DFT amplitude and angle of IMF1
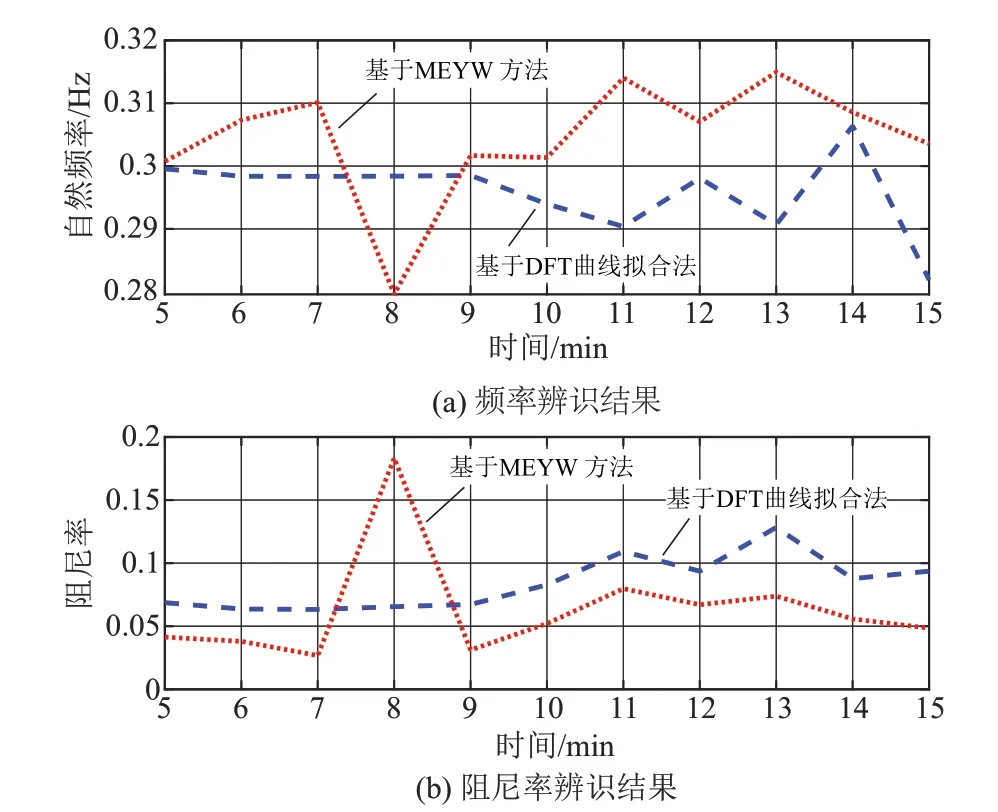
图5 模拟数据IMF1频率和阻尼率的辨识结果Fig.5 Frequencies and damping rates identification results of IMF1
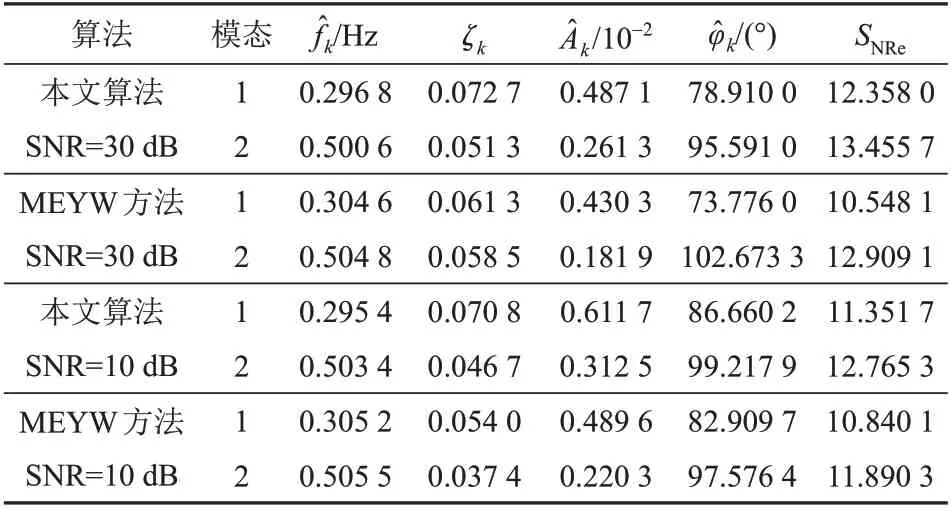
表4 模拟数据的辨识结果Tab.4 Identification results of simulated data
由表4可以看出,考虑量测噪声影响时,本文提出的辨识法能给出较为准确的频率值,而阻尼比和振荡幅值受系统运行方式的影响较大,所以信噪比越小,系统阻尼比和振荡幅值波动程度相对越大,但本文提出的方法波动相对较小,说明所提方法准确度高和抗噪性好。因此,文中采用的基于DFT 曲线拟合的辨识法比目前应用广泛的在线辨识MEYW法更准确,拟合精度SNRe如图6所示。
对比图6 中2 个分量的拟合精度SNRe可以看出,弱阻尼辨识结果比高阻尼辨识结果更准确,阻尼比越小,振荡平息时间也越长,一段时间后该模式信号分量相对于噪声仍占据主导地位,同时也可看出环境噪声越弱,信噪比越高,辨识精度越高。

图6 模拟数据拟合精度图Fig.6 Fitting precision diagram
该方法的计算时间与VMD分解个数、采样频率、数序列长度、数据窗滑动步长以及时间窗长度直接相关,VMD计算时间占比较大,但相对于EEMD 计算时间能减少很多,同时低通滤波后可减少分解个数,提高运行速度。由于MEYW法中AR模型的阶数比DFT拟合法的阶数高,相比较,本文辨识方法运行时间短。以MATLAB 2018 版进行编程,完成上述PMU模拟数据分析,SNR为30 dB 时低通滤波后VMD 分解个数为3,计算时间为6.372 7 s,基于DFT 曲线拟合辨识运行时间为0.927 8 s,耗时7.518 9 s,占空比为0.835 4%,完全满足在线应用要求。
3.2 实测数据模态辨识
以某实际系统PMU录波数据为例,分析系统低频振荡特征。实际系统采样频率为0.033 3 s,选取时长为15 min 的部分量测信号,实测数据减去额定频率60 Hz,得到实际频率的波动如图7所示。
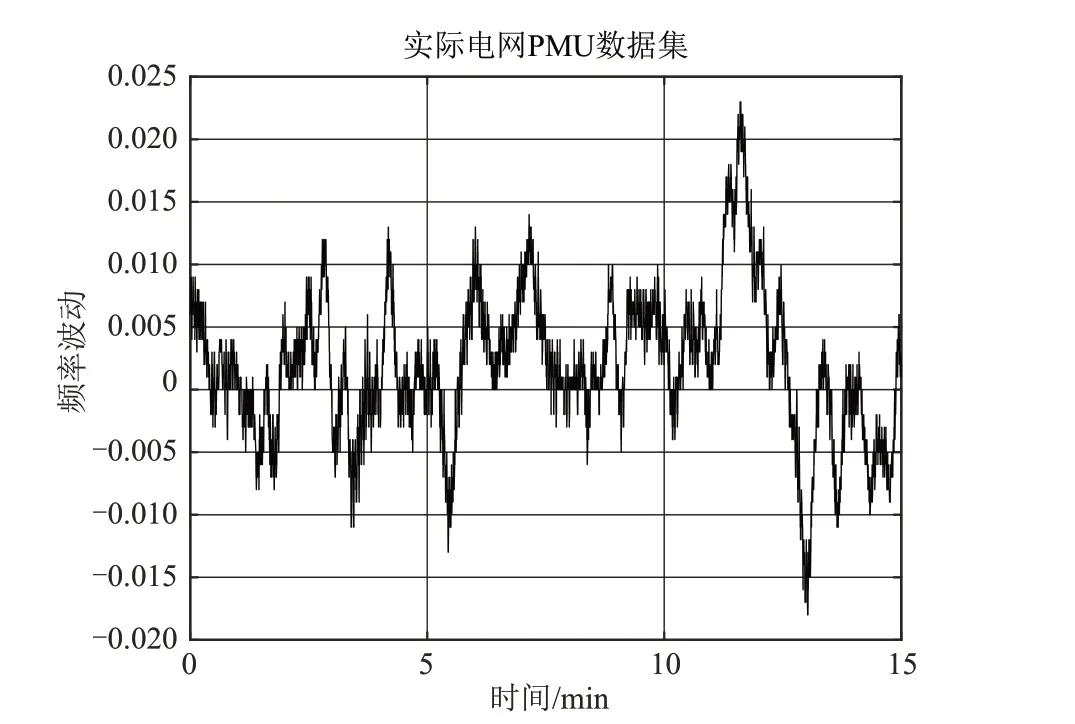
图7 某电网实测频率波动Fig.7 The measured frequency fluctuation of a power grid
VMD分解时经巴特沃斯低通滤波处理可以减少VMD分解个数,提高运行速度。本案例中,模态个数为5时最大相关系数大于阈值0.1,故取模态个数为4。VMD分解得到各分量及其频谱如图8所示,得到第一个IMF 分量为中心频率为0 的直流,同时得到3个不同频率段的信号,取危害较大的区域间低频振荡的信号IMF1 和IMF3,用本文方法进行模态辨识,辨识时采样频率为30 Hz,自相关函数的有效持续时间为20 s,数据窗长设为5 min,相邻数据窗间隔为1 min。此时得到辨识结果如表5 所示,IMF1分量的幅值和角度如图9所示,实测数据2个区间低频振荡模态分量的频率和阻尼比的辨识结果如图10所示,拟合精度如图11所示。通过对比结果可知,本文所提方法准确度高、抗噪性强,MEYW方法受随机测量噪声影响较大,同时通过对比拟合精度也验证了阻尼率越小,拟合精度越高。
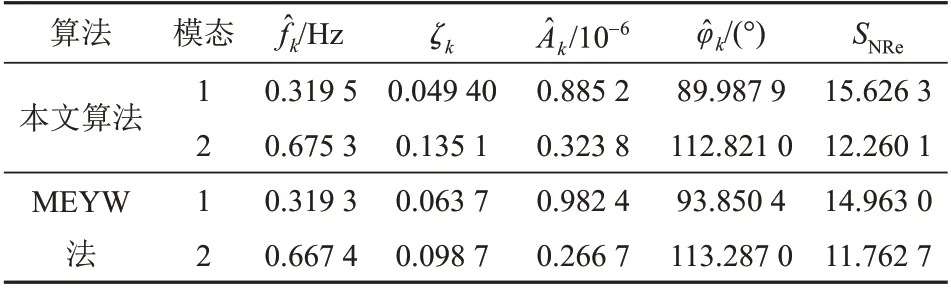
表5 实测数据辨识结果Tab.5 Identification results of measured data
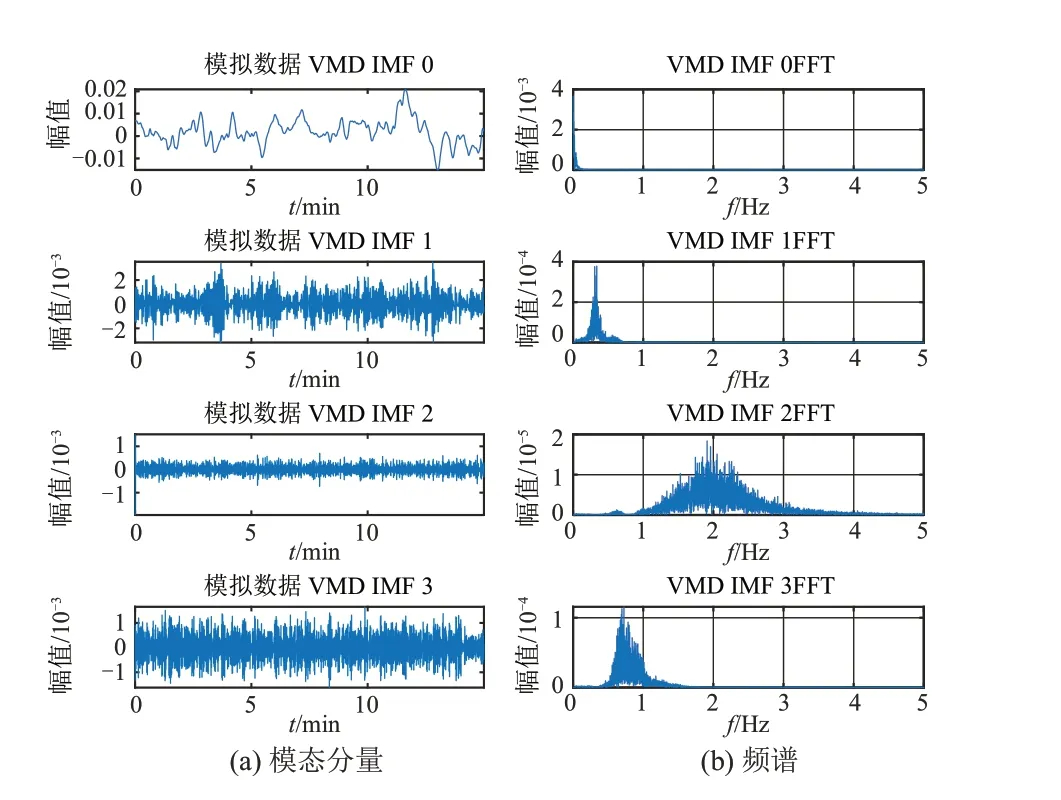
图8 某电网实测频率数据的模态分量及频谱Fig.8 Modal components and spectrum of a power network measured frequency data
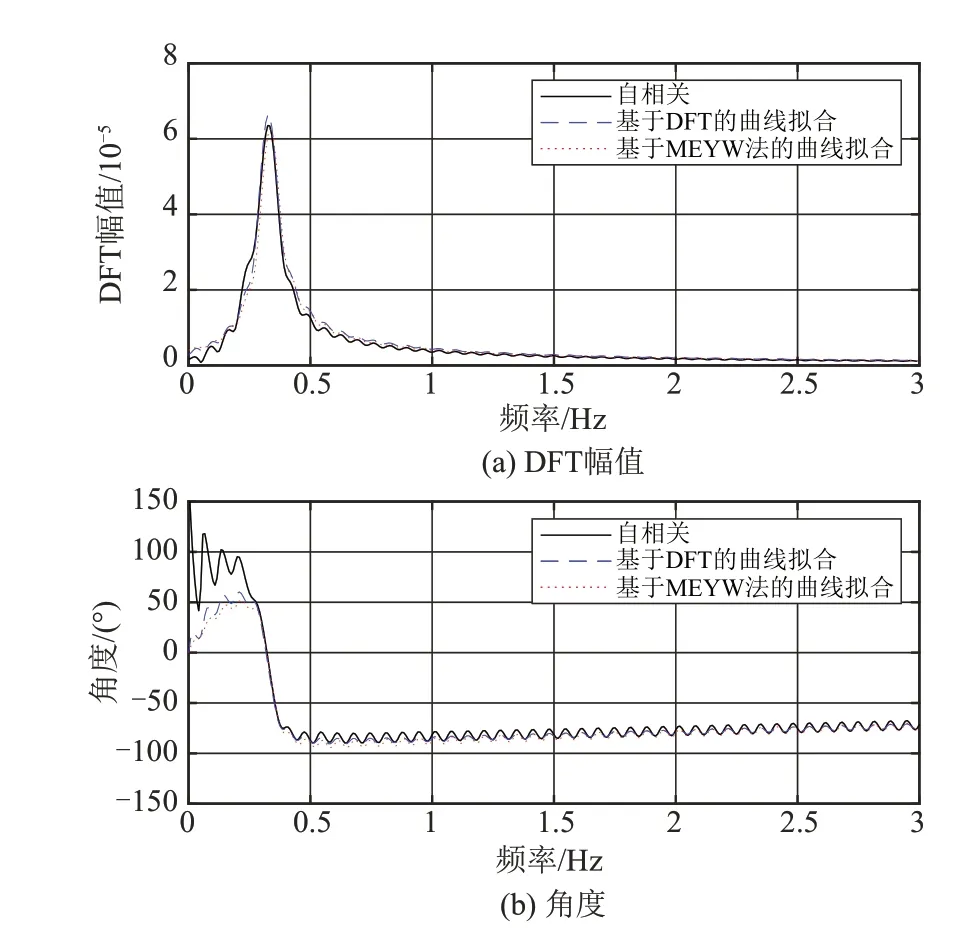
图9 实测数据IMF1分量的DFT幅值和相角Fig.9 IMF1 DFT amplitude and angle of measured data
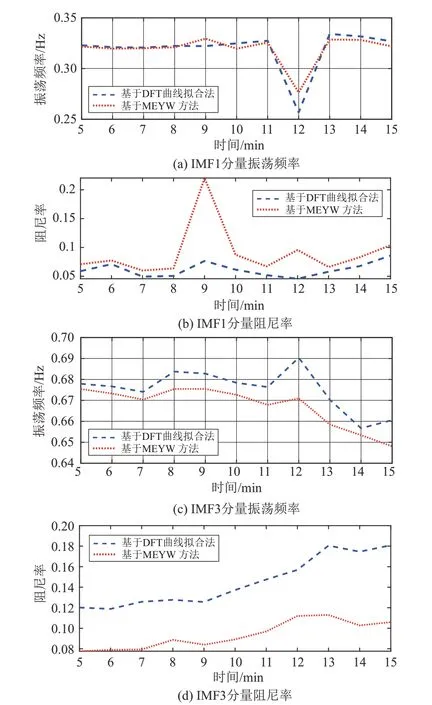
图10 实测数据2个模态的辨识结果Fig.10 Two modes identification results of measured data

图11 实测数据拟合精度Fig.11 Fitting accuracy of measured data
在实测数据辨识过程中,采样频率较低,为30 Hz,同样在MATLAB 2018 版本上运行程序。低通滤波后VMD 分解个数为4,运行时间为8.404 8 s,总耗时为9.551 s,占空比为1.061%,提高了机电小干扰稳定评估的实时性。
以上结果表明,由于VMD 算法和基于DFT的曲线拟合法都具有较好的噪声鲁棒性,参数辨识结果精度较高,辨识曲线平滑,符合实际的波动情况,并且计算速度满足在线应用要求,在用于实际量测数据分析时,同样取得了很好的辨识效果,证明该方法能够有效分解信号及准确提取低频振荡模态参数。
4 结论
以类噪声数据为基础,应用改进VMD算法进行数据的预处理,提出一种基于DFT曲线拟合的电力系统低频振荡信号识别方法。得出以下结论:
1)利用改进VMD 分解方法可有效消除直流分量或趋势项,并能准确提取出低频振荡信号,抗噪性好;
2)利用自相关函数保持原信号振荡模态参数特性,提出基于自相关函数DFT曲线拟合的模态参数辨识方法,通过DFT峰值个数可确定信号所含低频振荡模式的数量,运行时效性强;
3)采用模拟PMU 数据和某电网的实测数据计算分析,验证了所提方法的准确性和有效性。该方法可用于环境激励下的电力系统低频振荡在线模态参数辨识。
