特殊卷簧的刚度及应力分析
2022-03-17姜旭涛黄志辉王玉辉秦晓特
姜旭涛,黄志辉*,王玉辉,秦晓特
(1.西南交通大学牵引动力国家重点实验室,四川成都 610031;2.湖南铁路科技职业技术学院,湖南株洲 412006)
平面涡卷弹簧(简称卷簧)是用细长等截面金属材料绕制而成的平面涡卷形弹簧,广泛应用于各种机械设备中。其工作时,一端固定,另一端施加转矩,使材料产生弯曲变形。当外界对卷簧做功后,这部分的功就转化为弹性变形能;当卷簧工作时,其弹性变形能逐渐释放,驱动机构运转而做功。卷簧按其簧圈接触与非接触,可分为接触型卷簧和非接触型卷簧。接触型卷簧常用作储存能量,如各种原动机构。非接触型卷簧常用来产生反作用转矩,如电机电刷的压紧弹簧[1−4]。
现有一批用于汽车坐垫调角器的特殊卷簧,共计20 万个,已投入使用。该类特殊卷簧最内圈卷紧在芯轴上,其簧圈形状为正方形,而非一般圆形或半圆形,且最内圈与中间圈的簧圈之间存在过渡圆弧,最外圈簧圈延伸出一段弯曲扭臂。在工作转矩的作用下,该卷簧扭臂可达到的最大扭转角为45°,且在工作40 万次后发生疲劳破坏。为计算卷簧扭臂达到最大扭转角时所受最大工作转矩及研究卷簧在最大工作转矩状态下所受应力情况,本文基于HyperMesh 与ANSYS 联合仿真有限元分析方法,对该卷簧的刚度及所受应力进行研究,并结合理论计算与仿真、试验结果对行业标准JB/T 7366—1994《平面涡卷弹簧设计计算》中该卷簧的适用性进行分析。
1 卷簧研究模型
该卷簧未受外转矩时其簧圈未接触,属于非接触型卷簧。其材料采用65Mn,经过热处理后其维氏硬度HV 可达到411~478。簧圈外径D=15mm,卷紧在芯轴上的最内圈簧圈内表面边长分别为d1=5.3mm,d2=4.2mm,节距t=0.4mm,簧圈延伸出的扭臂弯曲半径R=10mm,材料厚度h=1mm,宽度b=4.5mm,其尺寸标注及转矩施加如图1 所示。
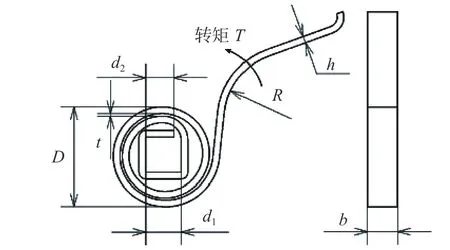
图1 卷簧尺寸标注图
2 卷簧有限元计算
本文通过CATIA 软件建立卷簧三维模型,将其以stp 格式导入HyperMesh,对模型划分网格,赋予材料属性,设置单元属性,建立接触、施加载荷及边界条件等,然后将输出的cdb 模型导入ANSYS中进行计算[5]。
2.1 卷簧有限元模型建立
卷簧采用65Mn 弹簧钢材料,需在HyperMesh中赋予的材料属性[6]如表1 所示。

表1 65Mn 材料属性
实际工作中,通过最内圈簧圈卷紧在芯轴上来实现对卷簧的固定约束。在仿真分析中,为了减少非线性接触的设置,提高有限元计算效率,本文通过卷紧在芯轴上的最内圈簧圈内表面节点进行全约束来等效替代芯轴对卷簧的约束。
根据实际工作情况,卷簧在转矩作用下发生变形的过程中,簧圈之间存在接触,所以在HyperMesh中需要对各圈簧圈内、外表面进行非线性接触设置。
在有限元模型中,对卷簧转矩的施加需要转化成力乘以力臂,计算公式[7]为

式中:T为对卷簧施加的转矩,N·mm;F为施加在扭臂上的力,N;L为等效力臂长度,mm,根据实际工作情况,卷簧等效力臂L=16.76mm,为定值。转矩T随着施加力F的变化而变化。
采用MASS 质量单元与RBE3 刚性单元,将卷簧扭臂的受力节点耦合为一个节点,并在卷簧中心位置建立空间柱坐标系,然后将力F沿柱坐标系施加在耦合的受力节点上。HyperMesh 处理后的卷簧有限元模型如图2 所示。
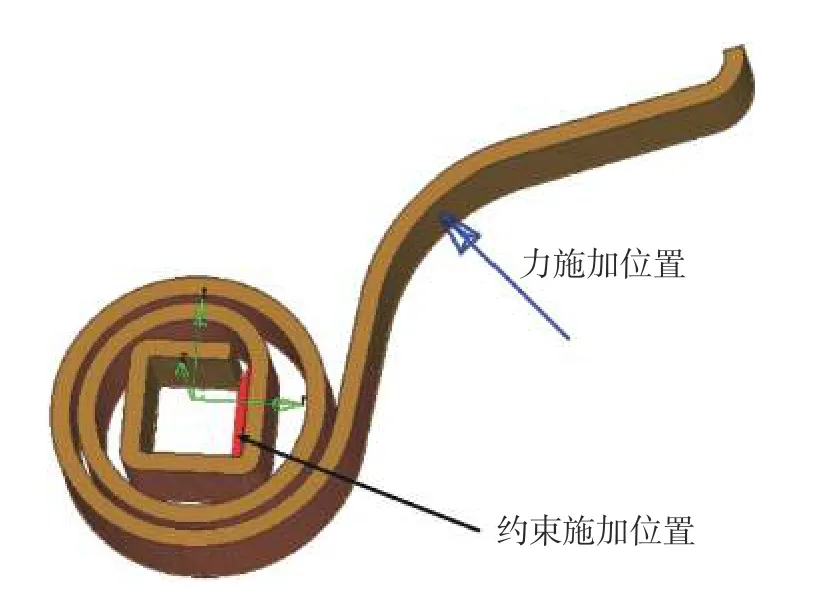
图2 卷簧有限元模型
为研究卷簧在达到最大扭转角45°时所应施加的转矩大小和所受应力情况以及刚度随转矩的变化情况,对卷簧施加逐次递增5N 的力,根据式(1),计算施加逐次递增83.80N·mm 的转矩,直至卷簧扭转角达到45°。
2.2 卷簧有限元模型计算结果
将HyperMesh 处理的有限元模型导入ANSYS中进行求解,经测量,可得到卷簧扭臂的扭转角φ,如图3 所示。
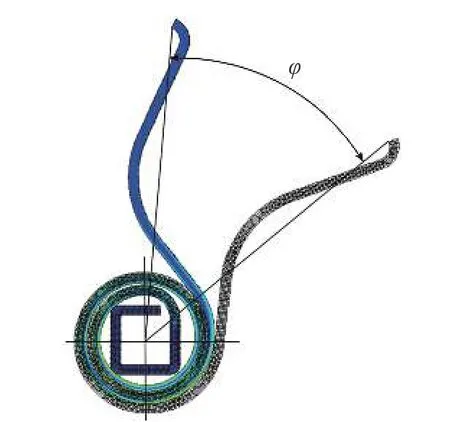
图3 卷簧扭转角测量示意图
经测量,卷簧扭转角达到45°时,所施加转矩为1089.40N·mm,在该转矩作用下卷簧的Von-Mises等效应力云图如图4 所示。

图4 最大转矩作用下卷簧Von-Mises 等效应力云图(单位为MPa)
转动刚度与扭转角的关系式[8]为

式中:k为卷簧刚度,N·mm/(°);φ 为卷簧扭转角,(°)。
将测得的各组转矩下的扭转角代入式(2)可以得到各组转矩下有限元计算的刚度,如表2 所示。卷簧刚度随转矩的变化规律如图5 所示。

表2 转矩—刚度对应关系表

图5 卷簧刚度—转矩曲线图
2.3 卷簧刚度分析
由表2 及图5 可知,卷簧刚度随转矩的逐次增加而不断增大,在施加转矩不超过335.20N·mm 的范围内,刚度呈非线性增长;但当转矩超过335.20 N·mm 后,刚度呈近似线性增长。
对卷簧有限元计算结果进行观察分析发现,当施加转矩达到335.20N·mm 时,卷簧部分簧圈发生接触,如图6 所示。卷簧簧圈接触相当于接触部分簧圈厚度增大,且随转矩的增加,接触面积逐渐增大,从而导致在转矩达到335.20N·mm 后卷簧刚度呈近似线性增长。
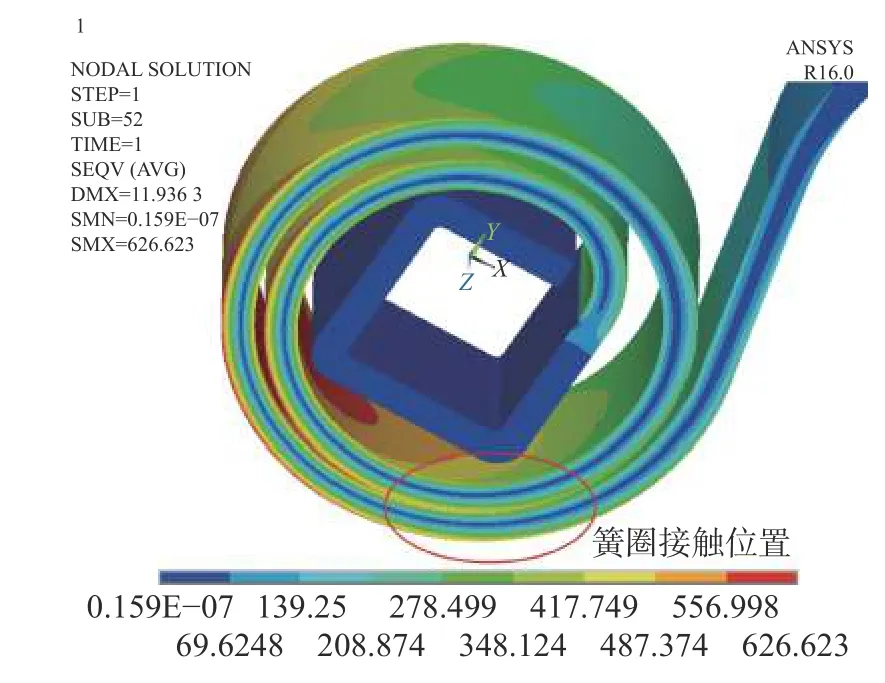
图6 卷簧簧圈接触示意图
将卷簧转矩达到335.20N·mm 后的刚度—转矩曲线进行线性拟合,得到刚度k与转矩T的拟合曲线k=9.46×10-3T+13.38,如图7 所示。
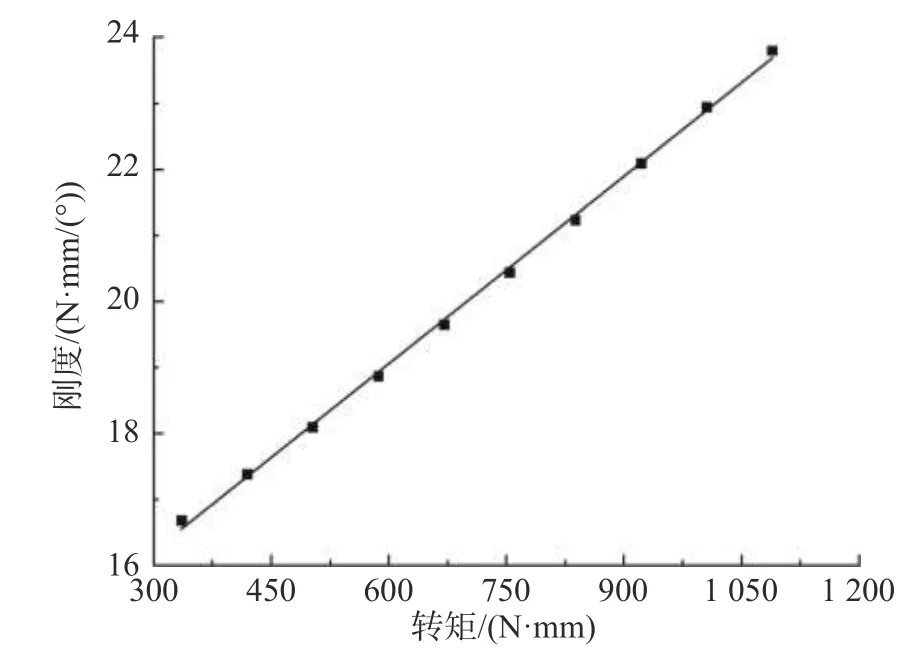
图7 刚度—转矩线性拟合曲线图
为保证在施加转矩不超过335.20N·mm 的范围内刚度—转矩拟合曲线的准确性,将施加力的间距降低为2N,根据式(1),即为向卷簧施加逐次递增33.52N·mm 的转矩。
将HyperMesh 处理的有限元模型导入ANSYS中进行求解,并测量各组转矩下的扭转角,根据式(2)可以得到在施加转矩不超过335.20N·mm 的范围内转矩—刚度对应关系,如表3 所示。
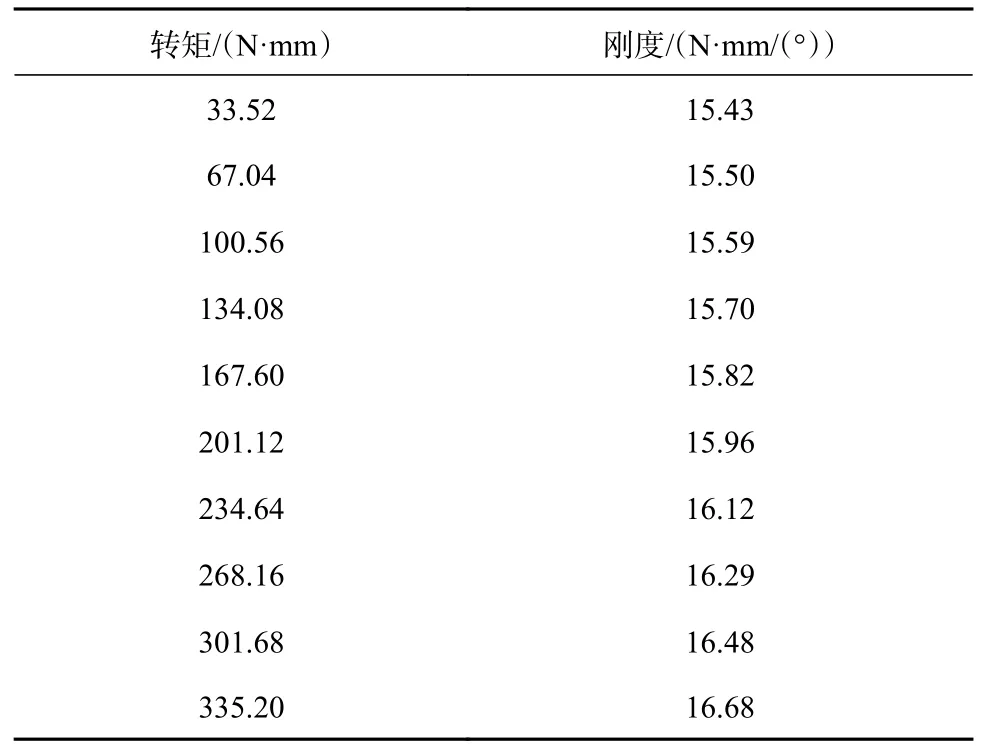
表3 转矩—刚度对应关系表
以所施加的转矩为横轴,以卷簧刚度为纵轴,对表3 数据进行多项式拟合,得到刚度k与转矩T的二次多项式拟合曲线k=7.28×10−6T2+1.48×10−3T+15.37,如图8 所示。

图8 刚度—转矩多项式拟合曲线图
综上所述,卷簧刚度与转矩的关系式为:
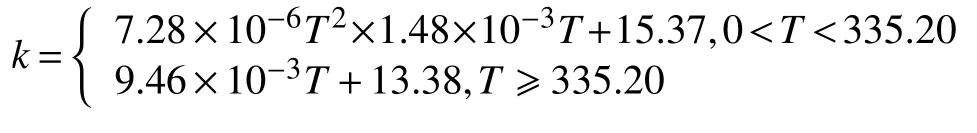
2.4 卷簧应力分析
由图4 可知,卷簧在最大工作转矩状态下所受最大应力σm=1557.18MPa,位于卷簧中间圈内表面且靠近最内圈簧圈缺口对角的位置,其局部等效应力云图如图9 所示。
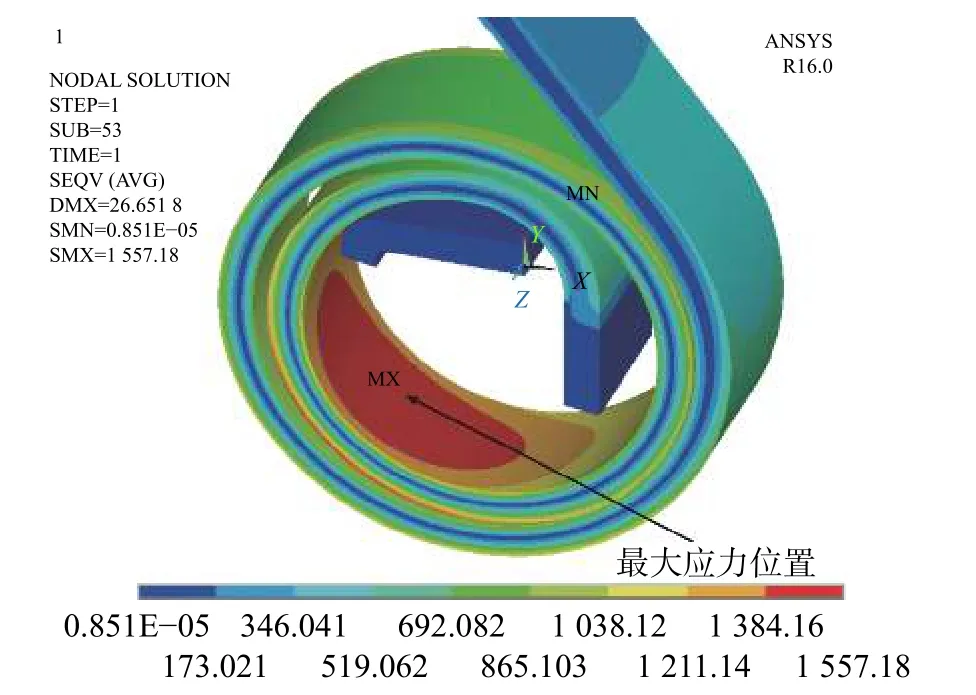
图9 最大转矩作用下卷簧局部Von-Mises 等效应力云图(单位为MPa)
根据行业标准JB/T7366—1994《平面涡卷弹簧设计计算》,当转矩作用次数大于105时,卷簧材料许用应力[9]为

式中:[σ]为卷簧许用应力,MPa;σb为材料抗拉强度,MPa。
65Mn 的强度——维氏硬度换算公式[10]为
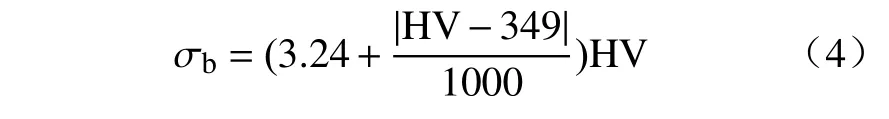
式中HV 为维氏硬度,取HV=450。
根据式(4)可知,热处理后65Mn 的材料抗拉强度σb=1503.45MPa。将其代入式(3)可得,卷簧材料许用应力[σ]=902.07MPa。
根据有限元计算结果,卷簧所受最大应力σm=1557.18MPa,大于材料许用应力,不满足强度校核,因此卷簧在工作40 万次后便发生疲劳破坏。
综合分析2.3 节及2.4 节的结果可知,本文有限元分析方法及计算结果可对该类特殊型式卷簧的刚度、应力分析提供参考。
3 卷簧疲劳寿命测试
将卷簧最内圈方形簧圈安装在芯轴上完成固定,然后对卷簧施加转矩,使其扭臂从初始位置扭转45°后又恢复至初始位置。
该卷簧在经受40 万次循环转矩后发生疲劳破坏,其断裂情况如图10 所示。

图10 卷簧疲劳寿命试验结果
结合图6 及图10可知,该卷簧发生疲劳破坏的位置在最外圈簧圈在工作时与中间圈簧圈的接触处,而并不在卷簧最大应力处。可见,簧圈之间发生接触产生的接触应力会导致卷簧疲劳寿命降低。
4 标准适用性分析
由于本文卷簧模型结构特殊,其最内圈簧圈形状为正方形,且最内圈与中间圈簧圈之间存在过渡圆弧,最外圈簧圈延伸出一段扭臂;而一般卷簧最内圈簧圈多为圆形或半圆形,且无延伸扭臂,如图11所示:因此,二者结构存在较大差异,无法直接判断该特殊卷簧是否适用行业标准JB/T7366—1994《平面涡卷弹簧设计计算》中的刚度、应力计算。本文将从刚度和应力2 方面对理论计算结果和仿真、试验结果进行对比,分析该标准的适用性。

图11 一般卷簧型式
4.1 刚度对比分析
根据行业标准JB/T7366—1994《平面涡卷弹簧设计计算》,卷簧刚度计算公式为

式中:E为材料弹性模量,MPa;K1为系数,外端回转时K1=1.25;l为材料工作圈展开长度,mm。
根据式(5)可知,理论刚度与转矩恒为线性关系,与仿真结果中刚度与转矩在簧圈接触前为非线性关系不符。
4.2 应力对比分析
根据行业标准JB/T7366—1994《平面涡卷弹簧设计计算》,卷簧应力计算公式为
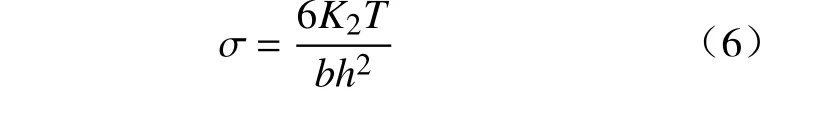
式中:σ为卷簧所受最大应力,MPa;K2为系数,外端回转时,K2=2。
将卷簧材料宽度、厚度以及最大工作转矩代入式(6)可得,理论最大应力σ=2905.07MPa。
通过对比发现:卷簧所受最大应力理论计算结果σ=2905.07MPa 与仿真计算结果σm=1557.18 MPa 差异较大;理论计算结果远大于许用应力[σ]=902.07MPa,与试验情况中卷簧在最大转矩作用下工作40 万次后才发生疲劳破坏的结果不符。
综上可知,该特殊卷簧不适用行业标准JB/T 7366—1994《平面涡卷弹簧设计计算》来进行刚度、应力的计算。本文的有限元计算结果可为该标准的补充、修订提供一定参考。
5 结论
1)该特殊卷簧在工作过程中簧圈发生接触,其刚度随转矩增大而增大,且在簧圈接触前二者呈非线性关系,在簧圈接触后二者呈线性关系。
2)该卷簧所受最大应力为1557.18MPa,位于卷簧中间圈内表面且靠近最内圈簧圈缺口对角处。
3)该卷簧在经受40 万次循环转矩后发生疲劳破坏,断口位于最外圈簧圈在工作时与中间簧圈的接触处,而并不在卷簧最大应力处。可见簧圈之间发生接触产生的接触应力会导致卷簧疲劳寿命降低。
4)JB/T7366—1994《平面涡卷弹簧设计计算》中刚度和应力计算公式不适用于本文所讨论的特殊卷簧。
5)本文的有限元计算结果可为行业标准《平面涡卷弹簧设计计算》的补充、修订提供一定参考。
6)本文有限元分析方法及计算结果可对该类特殊型式卷簧的刚度、应力分析提供参考。
