一种基于自外积异构信息网络的改进推荐模型
2022-03-17李林森范永全杜亚军
李林森,范永全,杜亚军,于 春
(西华大学计算机与软件工程学院,四川成都 610039)
随着网络的快速发展,信息过载问题非常明显,推荐系统应运而生,且在生活中扮演着非常重要的角色[1]。在推荐领域中,传统的做法就是协同过滤(collaborative filtering,CF)。协同过滤的主要思想是基于用户对物品的评分来推断用户可能喜欢的物品。太多太复杂的数据构成了一张庞大的异构网络图[2−4]。对于处理复杂多样的数据,一个新兴且流行的方式就是异构信息网络(heterogeneous information network,HIN)。有人将异构信息网络嵌入到社交网络中[5];还有人将异构网络嵌入到个性化推荐中[6]。如何处理异构网络嵌入是一个重要的问题。图1 展示了一些处理向量的方法。图中紫色、蓝色和绿色分别代表用户嵌入向量、物品嵌入向量以及交互特征。图1 中的(a)、(b)及(c),这些简单的操作并没有提取到更多有用的信息,如HERec 模型[7]采用了图(a)方式。文献[8−9]认为图1(b)和(c)这2 种处理方法都是低效的,因为它们假设不同维度之间是相互独立的。图1(d)考虑了不同维度之间的交互,用于提高推荐系统的性能,其典型模型有ONCF[10−11]。当然也有相互结合的模型,如PNN 模型,它结合了内积和外积操作来增强推荐系统性能[12]。很少有人将外积集成到基于异构网络的推荐系统中。值得注意的是,HopRec 模型[13]将用户与物品向量进行外积得到特征矩阵,用于提高推荐系统的性能。但是它忽略了一个问题就是嵌入向量自身不同维度交互所暗藏的有用信息。除了其中暗藏的信息,不同维度之间的特征组合也是一种非常有用的信息。目前,很少有人对用户或物品自身做外积来提取它本身在嵌入时丢失却暗含的有用关系。为此,本文提出一种基于自外积的异构信息网络模型(HSopRec模型)用于改进推荐系统的性能。
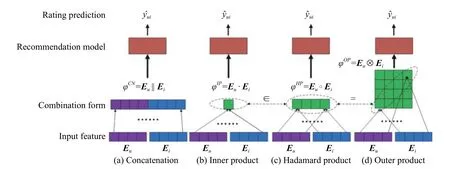
图1 不同形式的嵌入
图2 是HSopRec 模型完整的结构图,包括异构网络、异构网络嵌入、特征交互矩阵、评分预测4 个模块。本文所做的贡献主要有3 点。
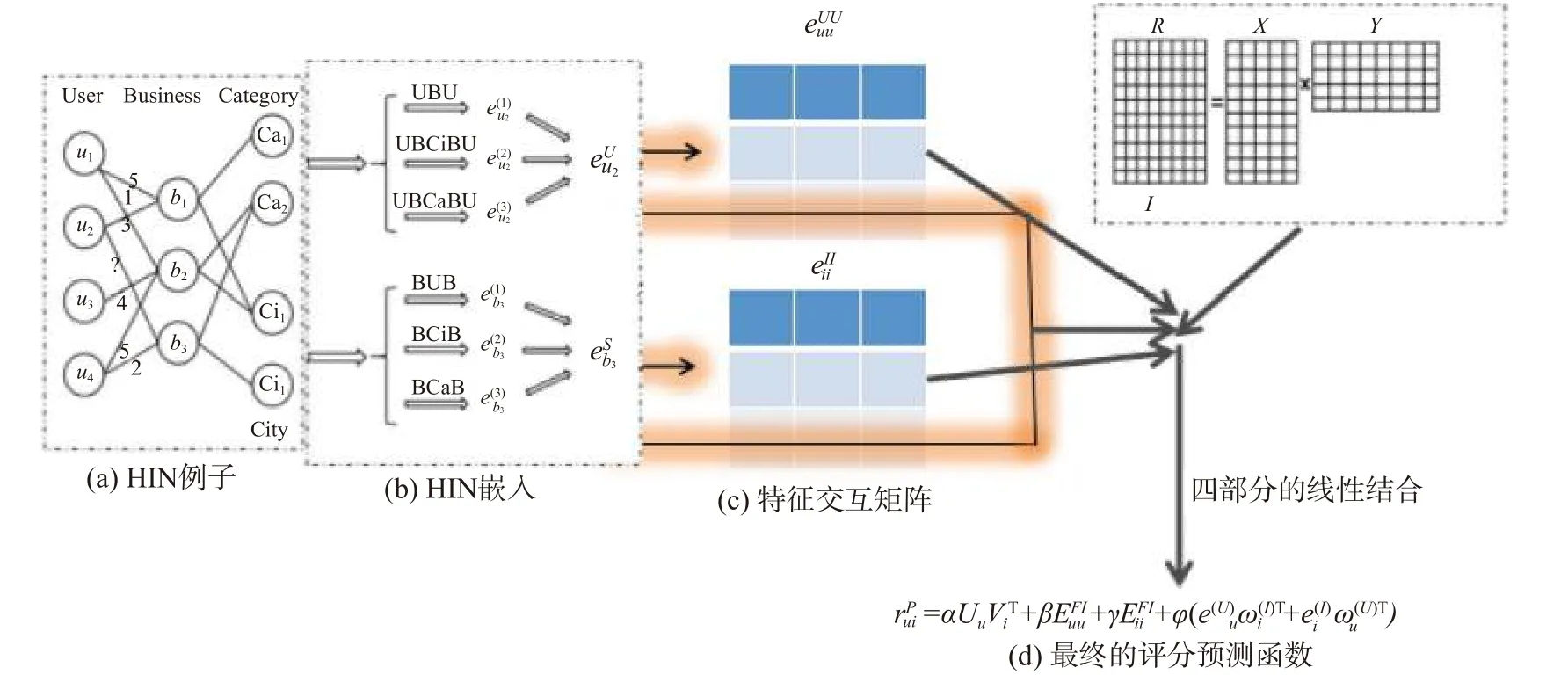
图2 HSopRec 的完整框架图
1)采用用户和物品之间的自身交互矩阵来挖掘用户与用户、用户与物品、物品与物品之间的直接或间接关系,称其为HERecUV 模型。
2)提出了HSopRec 模型。该模型是HERecUV模型[7]的扩展。该模型用2 个自特征交互矩阵加上用户与物品线性拼接的向量一起作为辅助信息去扩展矩阵分解(matrix factorization,MF)模型。
3)在开放的商业数据集Yelp 上的实验结果证明了HERecUV 和HSopRec 算法的有效性。尤其是HERecUV 模型比HERec 模型[7],在RMSE 性能上有一个很大提升。
1 相关工作
本节从4 个方面对相关工作进行归纳总结。它们分别是异构信息网络、推荐系统、网络嵌入、异构网络嵌入用于推荐系统。
1.1 异构信息网络
在现实世界中,大多数各种类型的网络图都是由不同类型的节点和边组成的异构网络。异构网络既可以大到一个领域的网络,也可以小到一个班集体的关系网络。这些异构网络图结构复杂、语义多样,但是它们包含的信息是非常有用的。异构网络嵌入向量的相似性保存了整个网络的结构性,所以可以利用异构网络图分析方法来做相似度搜索,还可以利用异构网络图分析法去做聚类、分类以及推荐等。异构网络中的多类型节点性导致早期的同质网络嵌入法无法对其进行操作,将不同类型的网络节点嵌入到一个空间是不合理的[14]。传统的相似度搜索方法通常使用余弦相似度或欧几里得距离等,然而异构网络中不同的元路径包含不同的语义信息会导致不同的相似性;因此,异构网络中所存在的丰富语义和结构信息可以提高不同实体之间相似性度量的准确性。显然,一些聚类方法也是无法使用的,无法将不同类别的节点聚在一起,这是不合理的,比如谱聚类。最近异构网络的研究主要围绕如何对异构信息网络进行高质量的嵌入进行。
1.2 推荐系统
推荐系统就是网络中的用户导购。它帮助人们从海量的物品中找到可能感兴趣的物品。推荐系统应用领域广泛,例如电子商务、广告等。推荐系统模型一般分为3 大类。第1 类,基于历史交互信息的推荐系统,如经典的基于历史评分的协同过滤[15]和矩阵分解模型[16]。文献[17]通过跨域的方式来缓解冷启动;文献[18]提出采用用户评论和评分一起作为辅助信息来缓解传统方法所带来的冷启动问题。第2 类,基于上下文信息的推荐模型,也就是用额外的辅助信息结合传统模型来增强推荐系统的性能,如基于异构网络的推荐系统[19−20]。本文的HSopRec 模型属于此类。第3 类,随着神经网络的迅速发展,就有了基于神经网络的推荐系统[21−23]。
1.3 网络嵌入
网络嵌入就是将一个网络中的节点嵌入到一个低维稠密的空间中,通过向量间的相似性来折射网络中节点之间的结构信息。网络嵌入已经广泛用于推荐领域。当今,同质网络最流行的方法是通过等概率随机游走学习到节点的表示。其中,学习的思想类似于自然语言处理的word2vec、deepwalk 的改进版本、不采用等概率随机游走的node2-vec 等。
1.4 异构网络嵌入用于推荐系统
异构网络嵌入包含了很多有用的信息,通过提取其中有用的信息可以增强推荐系统的性能。文献[7]通过在元路径上的随机游走得到节点嵌入,然后把用户和物品向量拼接起来一起作为辅助信息集成到MF 模型中进行推荐。文献[18]利用图神经网络学习异构信息网络中节点的嵌入进行推荐。
2 预备知识
在本节中,将介绍本文中用到的一些基本术语。
定义1(异构信息网络)定义一个网络G={V,E}。其中G为一个网络,V为网络中节点的集合,E为网络中边的集合。Φ(•)和φ(•)分别是节点的类型映射函数和边类型的映射函数。这2 个函数将节点和边的类型映射到节点类型集合A和边类型集合R。S={A,R}是网络的结构图。如果|A|+|R|>2,就称网络G为一个异构信息网络。
定义2(Meta-path)在网络G={V,E}以及其结构S={A,R}中,存在元路径,简写为A1A2···AiAi+1。路径上的R是可以相同的,A也是可以相同的。
定义3(自特征交互矩阵)给定一个异构网络G和它的网络结构S,可以通过Deepwalk 得到每个节点的嵌入向量,向量自身做外积操作即可得到自特征交互矩阵。
3 HSopRec 模型
本节将从4 个部分详细地描述HSopRec 模型的整体流程和细节。其主要流程是:首先将异构信息网络嵌入到稠密的空间中,得到网络中节点的嵌入向量;然后通过得到的嵌入向量做自外积得到自特征交互矩阵,通过左乘行向量和右乘列向量参数得到一个标量即自特征交互值;接着通过嵌入向量和自特征值结合MF 模型得到评分预测函数;最后,通过评分函数得到损失函数并对其进行梯度下降寻找最优解,完成模型的训练。图2 展示了HSopRec 模型的完整结构图。如无特殊说明,本文中的向量都是行向量。
3.1 异构信息网络嵌入
通过3 步可以得到异构网络中节点的嵌入。如图3 所示。首先,给定异构网络图G={V,E}和一条元路径p∶,通过式(1)可以获得一个随机序列。
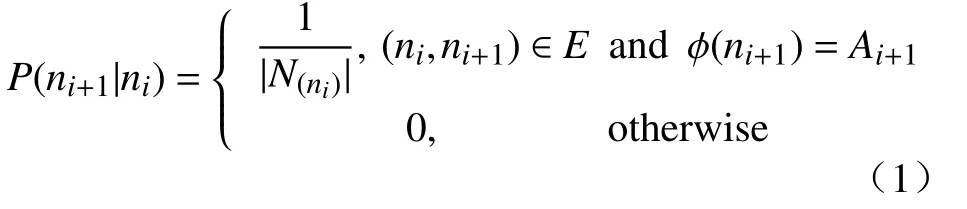
式中:ni和ni+1是第i和i+1 个节点,它们的类型分别为Ai和Ai+1;p为给定元路径;N(ni)是ni的邻居节点。给定起始节点和游走长度,通过式(1)可以得到一个随机序列。例如图3 中的电影异构网络,对于给定的元路径和行走起点,可以得到行走随机序列。给定元路径MDM,起始节点m1和行走步数,可以得到一个随机序列m1d2m2d3m3···。
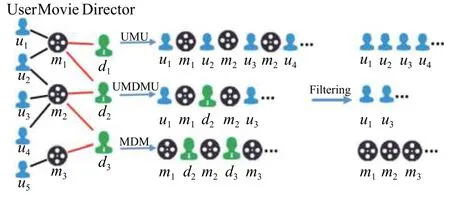
图3 同质网络的生成过程
然后,需要删除与起始节点类型不同的节点。具体地说,对于得到的随机序列m1d2m2d3m3···,把其中和m1不同类型的节点删除掉得到序列m1m2m3···,此时,可以把这个相同类型的随机序列看成一个同质网络,使用同质网络嵌入方法对每个节点进行嵌入,可以得到不同元路径上相同节点的不同表示集合。其中:P是所有元路径的集合;|P|是元路径集合的数量;是第l条元路径上的节点嵌入表示。
最后,通过融合函数得到最终的节点嵌入表示。
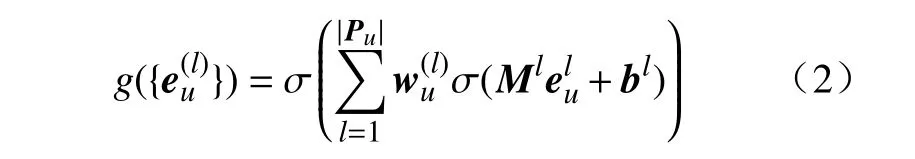
式中:σ(•)是Sigmoid 函数,用于对节点嵌入向量进行非线性变换;|Pu|是针对用户的元路径个数;分别代表在不同元路径上的偏好权重、节点嵌入向量的参数矩阵以及它的偏置。将也缩写表示为。
3.2 自特征交互矩阵

3.3 HERecUV 模型
本节将详细阐述HSopRec 模型所产生的评分函数。HSopRec 模型是对HERec 模型[7]的扩展。HERec 模型是基于矩阵分解模型(MF 模型)。MF 模型主要任务是将一个用户物品历史评分矩阵分解为2 个低维稠密的用户矩阵和物品矩阵,其表达式为


本文考虑利用用户嵌入与物品嵌入向量自己的不同维度之间隐藏的丰富特征交互信息,通过自外积捕获其潜在信息来扩展MF 模型。HSopRec使用的评分预测函数的表达式为

式中:α、β、γ和 ϕ是该模型的调优参数;和是自特征交互矩阵乘上参数之后所得的自特征交互值。
3.4 模型学习
在得到评分预测函数后,HSopRec 采用的目标损失函数,为
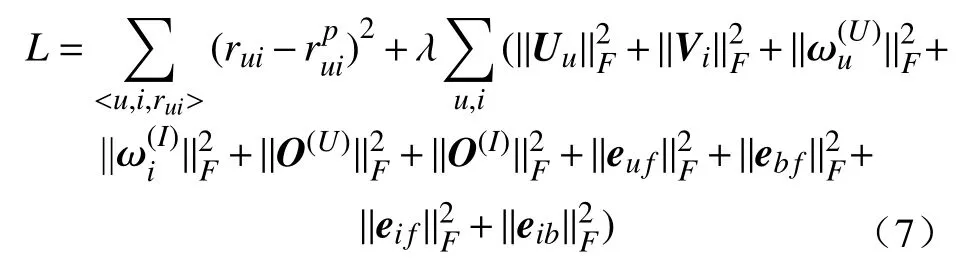
式中:L是模型HSopRec 的损失函数;rui是用户u对物品i的历史评价分数;是通过HSopRec 模型计算用户u对物品i的评分;λ 后面的一整部分是正则化惩罚项,这是为了防止过拟合;λ是各个参数正则化所带超参的统一形式;O(U),O(I)是对节点嵌入向量做融合时所有参数的总称。该目标函数通过随机梯度下降(SGD)来优化,所有参数更新根据的规则如下:

其中η 是该模型的学习率。带下标的λ是每个需要更新参数的正则化参数。是融合函数中的所有参数。本文利用Sigmoid 函数的连续性和易求导性,给出了各参数的融合函数的求导公式,为

4 实验
本节将在广泛使用的开放数据集上进行实验,并与其他推荐模型进行比较,来展示HSopRec 和HERecUV 模型的推荐性能。
4.1 评估数据集
表1、图4 分别为开放数据集Yelp 的数据信息和结构信息。图4 中大圆是实体,小圆是实体的属性。Yelp 是一个商业数据集。该数据集的稠密度非常稀疏只有0.08%。
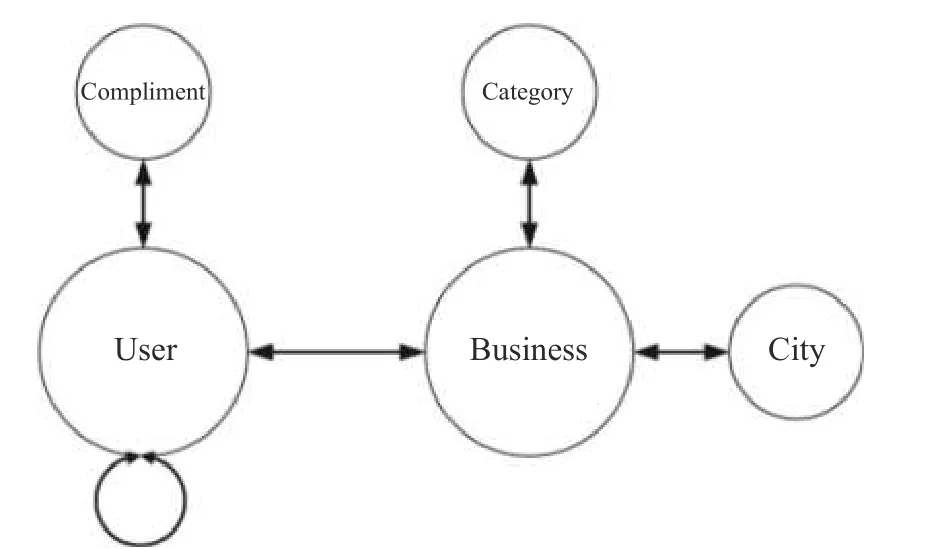
图4 Yelp 数据集的结构图
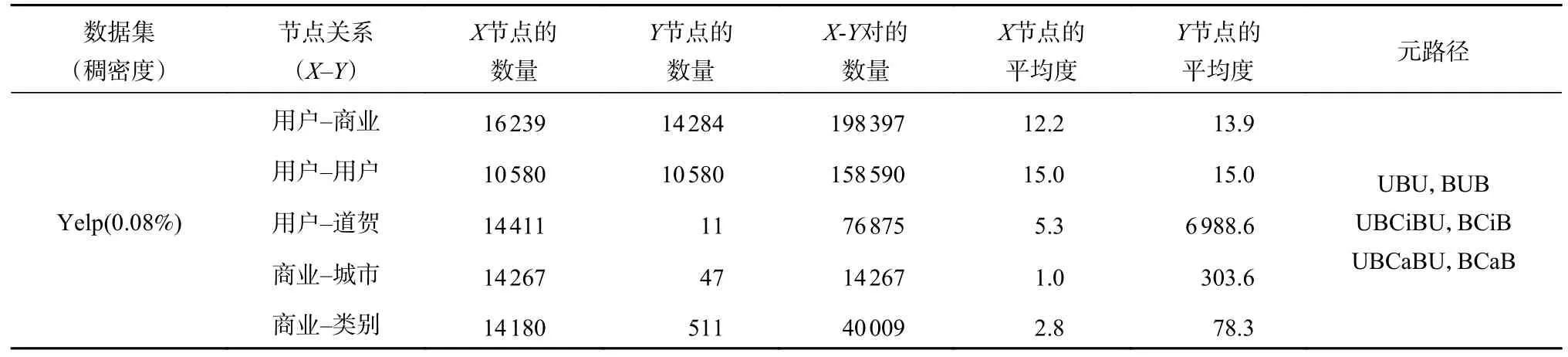
表1 Yelp 数据集的详细信息
4.2 评判标准
本文使用MAE(平均绝对误差)和RMSE(均方根误差)作为评价指标来比较不同模型之间的推荐性能,其定义为:
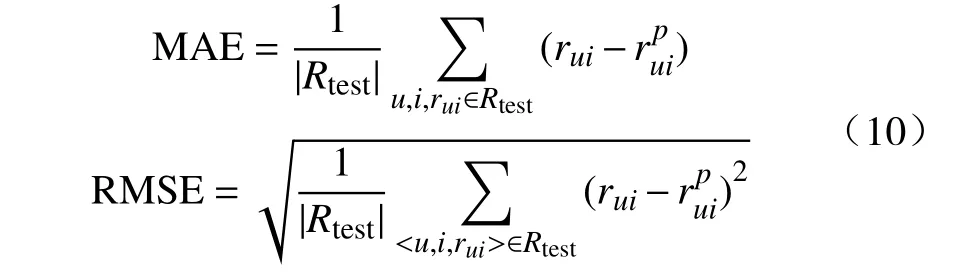
式中:Rtest是测试集;
4.3 比较模型
在实验中,将HSopRec 与下面模型进行比较。
PMF[24]:在假定用户和物品的特征矩阵服从高斯分布的前提下,将用户—物品评价矩阵分解为用户和商品的2 个低秩特征矩阵。
NMF[8]:它将用户—物品评价矩阵分解成2 个低秩非负矩阵。
HERec[7]:通过引入用户HIN 嵌入和物品HIN嵌入,扩展了矩阵分解模型。该模型的代码由作者提供(https://github.com/librahu/HERec)。
HERecUV:只考虑用户和物品嵌入信息的自特征交互矩阵来增强经典的矩阵分解。
HSopRec:集成自特征交互矩阵、用户HIN嵌入、物品HIN 嵌入和MF 的模型。
4.4 实验结果
在本节中,Yelp 数据集被划分为训练集和测试集,用来验证所提模型的有效性。设置Yelp 数据集的训练集与测试集的比例为8∶2。表2 展示了该实验的结果。除此之外,还对本次实验结果做了一个详细的总结。

表2 实验结果
3 种基于HIN 的推荐模型(HERec 模型、HERecUV 模型、HSopRec 模型)在推荐性能上明显优于传统的矩阵分解模型(PMF 模型、NMF 模型)。
与PMF 和NMF 模型相比,自特征交互矩阵和用户与物品HIN 嵌入的向量都可以有效地从HIN 中挖掘有用信息以提高推荐性能。此外,自特征交互矩阵增强的MF 模型得到的RMSE 比利用用户和物品HIN 嵌入的拼接向量得到的RMSE 要高得多。因此,用自特征交互矩阵挖掘出来的信息更接近真实信息。
对比HERec 模型和HERecUV 模型,虽然两者在MAE 上的得分相似,但HERecUV 模型在RMSE 上得到了很大的提高。可见,自特征交互矩阵比用户和物品HIN 嵌入的拼接向量能更好地模拟样本数据。换句话说,用它增强MF 模型能抓住更多用户对物品的真实喜好。
在所有的比较方法中,HSopRec 的推荐性能总体上是最好的。与HERec 模型相比,HSopRec 模型不仅利用了用户和物品本身的嵌入特征,而且还利用了它们自身的特征交互信息。实验结果表明,用户HIN 嵌入、物品HIN 嵌入和自特征交互矩阵增强MF 能有效提高推荐性能。
4.5 参数设置
为了公平和方便,对各种维度大小进行了调整,矩阵分解的向量维度设为10,从给定的元路径学习到的节点嵌入维数设为128。融合函数处理后的用户和物品最终嵌入维度与HERec 模型相同,分别为30 和10。为了减少计算负担,设置调优超参α、β、λ和ϕ是相等的,将其设置为α=β=γ=ϕ=0.5。这是表示它们每一部分都是同等重要的。设置学习率η=0.02,为了方便所有正则化参数都设置为0.1。
5 总结
本文提出了基于自外积异构信息网络增强的推荐方法,即HSopRec 算法。该方法具有较高的推荐性能,并且可以利用自特征交互信息提高推荐性能。实验结果表明,该模型具有更好的MAE 和更高的RMSE。从实验结果可以看出,自特征交互信息对提高推荐系统的性能起着至关重要的作用。
在今后的工作中,要把更多的非线性结合考虑进去,因为非线性组合在实践中可能更有效。虽然自特征交互矩阵隐含了丰富的关系,可以用来提高推荐系统的性能,但并不知道其自身相同维度的特征交互是否有作用。除此之外,随着深度学习的快速发展,也会考虑利用深度学习从异构信息网络中挖掘出更具有力量的潜在信息来提高推荐性能。
