SVR 算法的生物混液左旋多巴含量紫外光谱建模*
2022-03-17王文哲
王文哲
(江南大学物联网工程学院 无锡 214000)
1 引言
左旋多巴可以由酪氨酸通过羟化酶催化产生[1]。多巴和酪氨酸是合成各种蛋白质的原料。左旋多巴,属于儿茶酚胺。儿茶酚胺是体内非常重要的神经系统物质。它可以调节人体的神经系统和器官,还可以影响人体的新陈代谢[2~3]。建立一个测量模型不仅有助于检测血浆和尿液中的儿茶酚胺[4],而且对高血压、甲亢、糖尿病等疾病的临床诊断也具有重要意义。因此该研究具有重要意义。本文基于紫外光谱分析技术,建立了一种基于SVR 算法的左旋多巴酪氨酸混合溶液中左旋多巴含量的检测方法。
紫外线吸收光谱法是一种利用物质在紫外波段特定波长处的吸收特性来定性或定量研究物质的方法。在紫外可见光(200nm~800nm)范围内,大多数水溶性有机化合物具有吸收特性。紫外线光谱主要覆盖100nm~400nm 的波段,而200nm~400nm 的波段是近紫外线区域。通常,选择近紫外光谱进行定性或定量分析[5]。它具有良好的灵敏度,并由于其强大的选择性而被广泛使用[6]。
支持向量机算法[7](SVM)是一种基于统计的机器学习算法,由Vapnik 等提出。基本思想是在线性分类器中找到最佳分类表面。支持向量机回归(SVR)是基于SVM 的回归算法,它是从SVM 方法开发出来的用于解决分类问题的算法。它结合了变量的选择和回归模型的建立,以获得最佳的预测效果[8~10]。紫外光谱分析技术由于其灵敏性、可靠性、便利性、快速性和易推广性而被应用于生物发酵中。
2 实验部分
2.1 仪器设备
紫外光谱分析实验数据使用测量范围是200nm~750nm 范围的紫外-可见光谱光谱分辨率为2cm-1,积分时间为32s。用Python 建立紫外光谱数学模型对采集的紫外光谱数据进行分析。
2.2 左旋多巴酪氨酸混液校正集划分
在实验中,左旋多巴和酪氨酸的混合溶液由56 组光谱数据组成。使用Kennard-Stone(K-S)[11]算法,按照3:1 的比例将其分为40 个样品和16 个样品。分别用作校准样品集和验证样品集。K-S方法是一种有效且广泛使用的校正集选择方法。K-S算法基于每个光谱之间的欧几里德距离,并选择分布范围较广的代表性样本作为校准集样本,从而避免了人工选择的主观盲目性。
2.3 特征波长区间的选择
样品的化学成分和浓度不同时,其在不同波长处的吸光度也不同,紫外光谱图随之出现差异。本研究采用的多巴与酪氨酸的混液的紫外光谱图如图1 所示,为避免波段过宽造成光谱矩阵有大量冗余信息以及干扰,导致后续分析的准确度和效率降低,本研究首先对紫外光谱波段进行了优化提取,选择光谱信息较为丰富的251nm~300nm 波段作为优选光谱区。
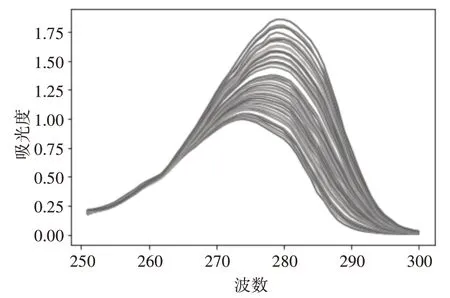
图1 左旋多巴与酪氨酸混液紫外光谱图
2.4 SVR算法
支持向量回归(SVR)是基于支持向量机(SVM)的回归算法,保留了最大间隔算法的主要特征:非线性函数可以由线性学习器在内核特征空间中获得,而不是与要素空间参数相同。相关参数控制系统的容量。像分类算法一样,学习算法需要最小化凸函数,其解决方案是稀疏的[12]。因此,需要选择适当的损失函数[13~14]。本文使用的损失函数是软间隔损失函数。

当x点的观察值y与预测值f(x)的差补偿预先给定的ε时,则认为在该点的预测值f(x)是无损失的,尽管预测值f(x)和观察值y不一定相等。
如图2,当样本点位于两条虚线之间时,则认为在该点没有损失。基于支持向量机(SVM)的规划算法就是ε-SVR。
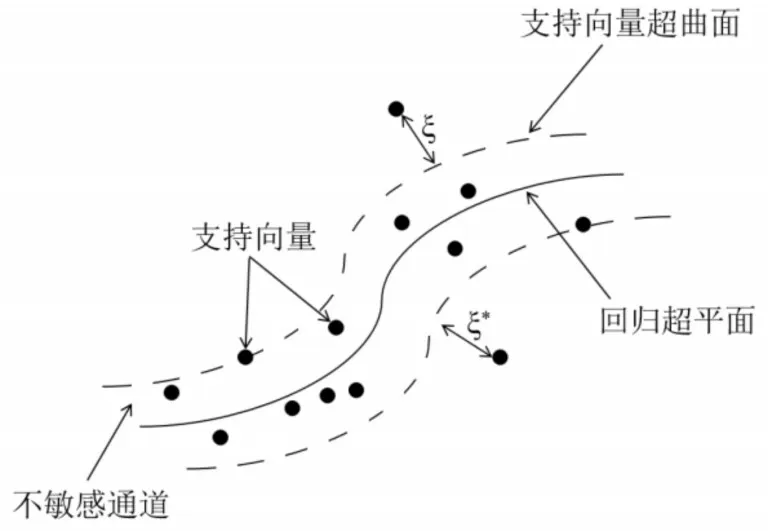
图2 支持向量样本和不敏感通道

在式(7)中,将点积替换为核函数k(xi,x),并且核函数可以执行低维空间数据输入以在高维特征空间中执行点积计算而无需知道映射φ。
目前,支持向量机算法的核函数有十多种,其中最常见的为以下几种:
线性核函数(Linear):
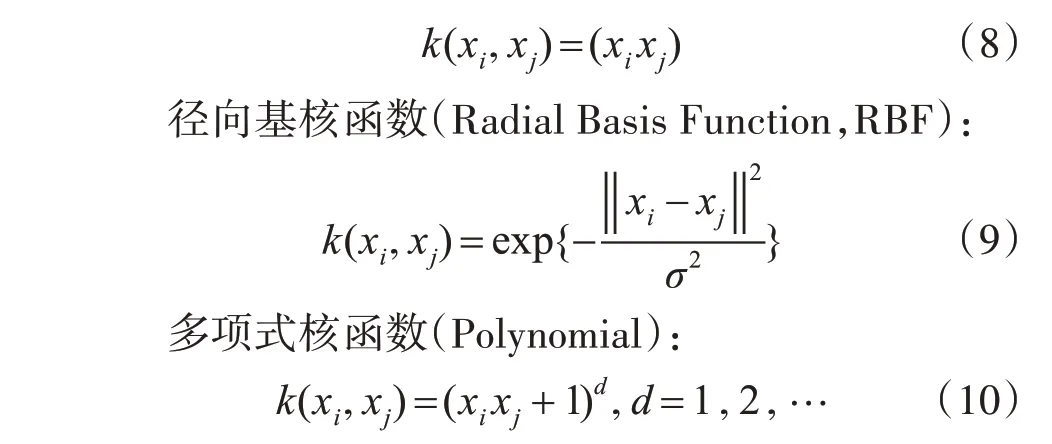
SVR模型优先确定核函数,核函数的选择将直接影响SVR的效果,另外核函数的参量对模型也会有一定影响。
这就是ε-SVR,与ε-SVR相比ν-SVR 是在上述支持向量回归机的改进,ε不敏感损失参数的选取比较难,所以引进另外一个参数ν(ν∈( ]0,1),ν 比ε容易选取。
3 结果与讨论
3.1 样本集划分
在定量建模之前需要对光谱数据进行校正集与验证集的样本划分,通常使用随机选择法(Random Selection,RS)、K-S法(Kennard-Selection)等算法。其中RS 算法由于划分样本的随机性较大,且本实验样本为酪氨酸与左旋多巴混合溶液的紫外光谱数据,可能导致样本划分不均匀的现象。故本文使用K-S 算法对样本集进行划分。使用K-S 算法选择样本分为以下三个步骤。
1)使用欧式距离计算样本集中样本之间的距离,选择样本集中距离最大的两个样本,放在校正集中。
2)对于其他样本,计算每个样本与第一步中选择的样本之间的欧氏距离,并选择距离最短的放入校正集。
3)重复步骤1)与步骤2),直到选出合适的校正集,其余样本组成验证集。
K-S 算法中,各个样本之间的距离公式为欧式距离,即为式(11)。
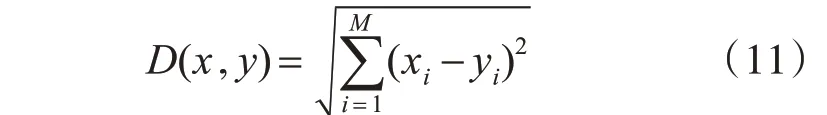
将剔除样本后的51个酪氨酸多巴混液按照3:1比例划分为38个校正集和13个验证集。
3.2 SVR参数优化
为了使回归模型准确反映仿真结果,需要设置模型参数。这些模型参数不易选择,不能直接给出。为此,采用粒子群算法搜索ν-SVR模型的最佳参数C 和ν以及ε-SVR 的参数C、γ。粒子群算法具体的优化方法如下。
步骤1:随机产生粒子的初始位置及初始速度。
步骤2:用ν-SVR、ε-SVR 回归训练每个粒子,并使用k 倍交叉验证的均方误差作为粒子群的目标函数值。
步骤3:通过迭代搜索并输出全局最优值。
步骤4:从搜索中获得的全局最优值用作回归的ν-SVR、ε-SVR模型的参数。
其中,ν-SVR 优化参数为C、ν;ε-SVR 优化的参数为C、γ。ε为默认值0.1。
3.3 评估指标
使用多个方法进行对比模型的评价指标包括相关系数(R)、预测均方根偏差(RMSEP)、相对误差(δ)、相对预测均方根误差(RRMSEP)。其中:
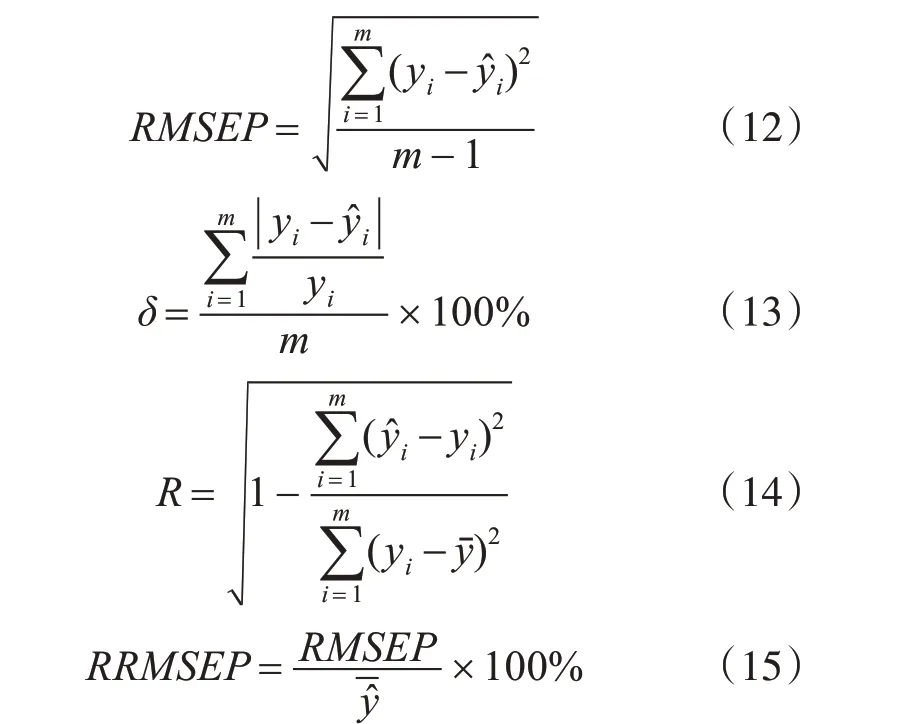
式中:yi为第i个样品的化学值;ŷi为第i个样品的预测值;m为验证集样本个数;yˉ为验证集化学值的均值。
3.4 实验结果
经过粒子群算法参数优化后的ν-SVR,线性核函数最优参数为C=511、ν=0.35;径向基核函数最优参数为C=41976、ν=0.65;多项式核函数最优参数为C=11739、ν=0.84。评估指标如表1 所示,三种核函数中径向基核函数的建模效果最佳,RMSEP 为0.826。其次为线性核函数,使用多项式核函数的建模效果一般。

表1 ν-SVR模型的评估指标
经过粒子群算法参数优化后的ε-SVR,线性核函数最优参数为C=356、γ=0.1;径向基核函数最优参数为C=6599、γ=0.1;多项式核函数最优参数为C=93、γ=0.1。评估指标如表2 所示,三种核函数中,径向基核函数建模效果最佳,RMSEP 较ν-SVR降低了接近0.2,其次为线性核函数。在两种支持向量回归机中,建模效果均为径向基核函数好于线性核函数好于多项式核函数。
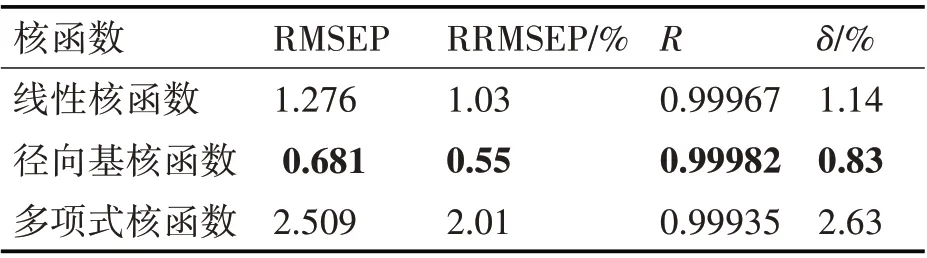
表2 ε-SVR模型的评估指标
接着将经典的PLS 算法加入比较中,如表3 所示,为ν-SVR、ε-SVR 的径向基核函数与PLS 实验对比。
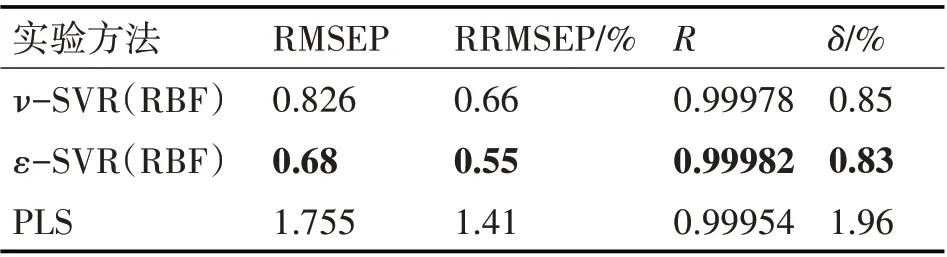
表3 模型验证结果对比
从表3 可以看出,三种建模方法,R 值均大于0.9995 说明建模效果较好,SVR 算法的建模效果好于PLS,其中,径向基核函数构建的ε-SVR 模型的拟合效果最好,RMSEP、RRMSEP、δ为0.68、0.55%、0.83%,相关系数R 为0.99982。在紫外光谱建模时,使用粒子群算法优化的ε-SVR可以达到更好的建模效果。
4 结语
两种SVR 算法对左旋多巴和酪氨酸混液紫外光谱数据的建模效果均好于传统的PLS模型,基于径向基核函数的SVR 算法的预测精度均好于线性核函数以及多项式核函数建立的SVR 算法。其中径向基核函数的ε-SVR精度建模效果优越,预测精度高,泛化能力强。侧面表明紫外光谱技术结合SVR 算法可对左旋多巴和酪氨酸混液中浓度的预测效果明显,且方法快速、准确、经济环保、易于推广。
