基于改进遗传算法的国内旅行交通规划研究*

于 雁 李小光

（青岛大学自动化学院 青岛 266071）

1 引言

随着中国全面进入小康社会，人们不再局限于物质消费，越来越重视精神文化满足。随着旅游业的快速发展，人们对已有的地域空间和距离的认识不断健全，时间距离和成本距离逐渐替代传统的空间距离被广泛应用于研究中［1］，在“四纵四横”客运专线建设全面展开形势下［2］，中国游客对于交通路线和外出成本的需求在逐渐提高。从黑龙江到海南岛，上海到乌鲁木齐这种长时间和多地点的外出旅行，进行合理的旅行交通规划，使得所需总费用最少，具有重要的现实和研究意义。

旅行交通规划与旅行商问题具有一定的内在联系，旅行商问题是一个典型的数学组合优化问题，已经被广泛应用到许多实际问题中［3～7］，如物流配送、飞机航线安排和产品的生产安排问题等。这些问题都可以通过数学变换转化为旅行商问题进行求解［8］。求解旅行商问题的方法有简单插值算法、模拟退火算法、蚁群算法和遗传算法等，其中，最受欢迎的是遗传算法［9］。传统的遗传算法存在易早熟收敛、后期收敛速度慢的缺陷，许多学者针对此问题对传统遗传算法进行改进并与其他算法相结合，满足了自身对不同问题的具体解决方法需求。罗金亮等［10］利用择向交叉遗传算法对远距支援干扰部署问题进行了研究；Sonmez A等［11］利用遗传算法对无人机的路径规划做了优化；王勇臻等［12］利用改进分组遗传算法求解了多旅行商问题；许宏志等［13］提出了一种仿细粒度的粗粒度并行模型，实现了双层并行的遗传算法在旅行商问题中的应用；易云飞等［14］通过将牛顿力学中的加速度因子映射到粒子群算法的惯性权重，改进粒子群算法对旅行商问题进行了研究；李敏等［15］利用遗传算法、蚁群算法和模拟退火算法对中国旅行商问题进行了仿真。

自然界中动植物的生老病死是固有的规律，当动物达到一定的年龄后，便会死亡。本文将动物会自然死亡的规律应用于遗传算法中，对个体编码时赋予年龄操作，将此改进遗传算法进行国内旅行交通规划，为人们的外出旅行提供最优化的旅行路线和旅行总费用。

2 旅行交通规划

旅行交通规划与旅行商问题相类似［16］，旅行商问题是以地点之间的距离总和为优化目标，使得距离总和最小。由于我国国内各个城市之间的距离相隔较远，必须要乘坐一定的交通工具前往。旅行交通规划是指推销员乘坐交通工具代替步行到达多个地点，并在到达地点无重复的情况下找到最终点再回到起点的总路径，使得所需费用最低。

旅行交通规划问题用数学语言描述为寻找一条巡回路径，目标函数为

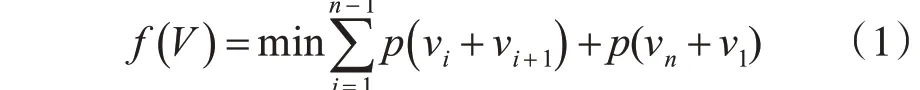
其中vi为城市号，i∈N，1 ≤vi≤n，p(vi,vj)表示城市i与城市j 之间乘坐交通工具所需费用，对于对称旅行交通规划问题有p(vi,vj)=p(vj,vi)。

3 遗传算法

对于旅行交通规划问题，通常应用遗传算法中的选择操作、交叉操作和变异操作。本文针对传统遗传算法存在的问题，对其进行改进，即在选择操作和交叉操作后加入年龄操作，最后进行变异操作。

改进遗传算法的流程图见图1。

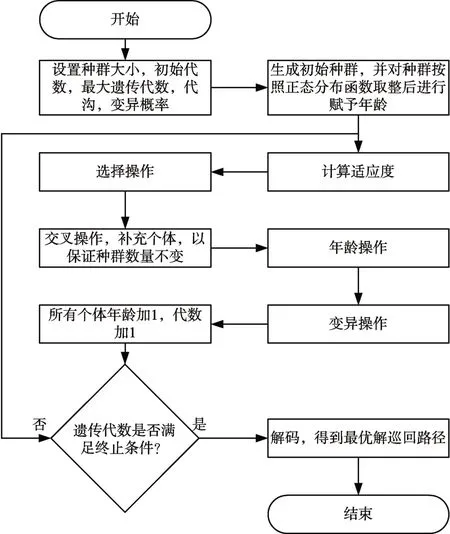
图1 改进遗传算法流程图

各个操作的具体内容如下。

选择操作：按个体适应度大小，从旧群体中选择部分个体到新群体。

交叉操作：根据适应度大小，利用轮盘赌注方法选择两个个体，交叉产生新个体。

变异操作：确定个体基因两个位置，将其对换。

年龄操作：判断个体年龄是否达到各种动物死亡年龄范围，若年龄进入死亡年龄范围，则删除该个体，并利用交叉操作，产生新个体，同时赋予该新个体年龄为0，以保证种群数量不变。

4 仿真实验与结果分析

以乘坐火车为旅行主要交通工具，在国内31个省会城市间，进行旅行交通路线规划。城市与城市之间有多趟和多种列车运行，具体交通工具按照以下规则进行选择。

1）城市之间有直达车，优先选择高铁；若无高铁，选择软卧。

2）城市之间无直达车，进行换乘，优先选择高铁；若无高铁，选择软卧。

3）前往台北，选择飞机。

将31个省会城市进行编号，见表1。

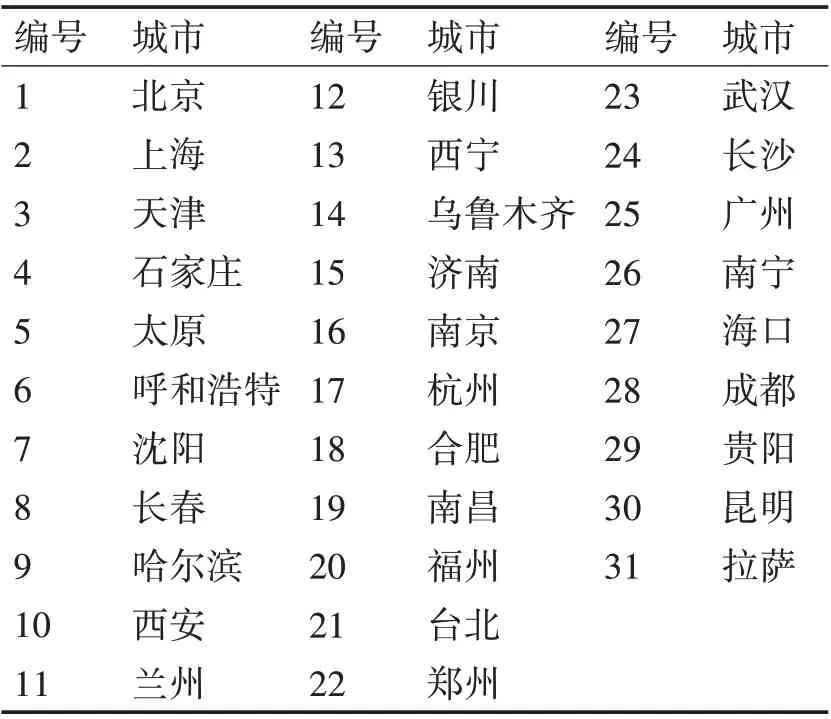
表1 编号与城市对应表

查阅中国运输系统价格表，获得各个城市之间的交通运输所需费用，费用表如表2所示。

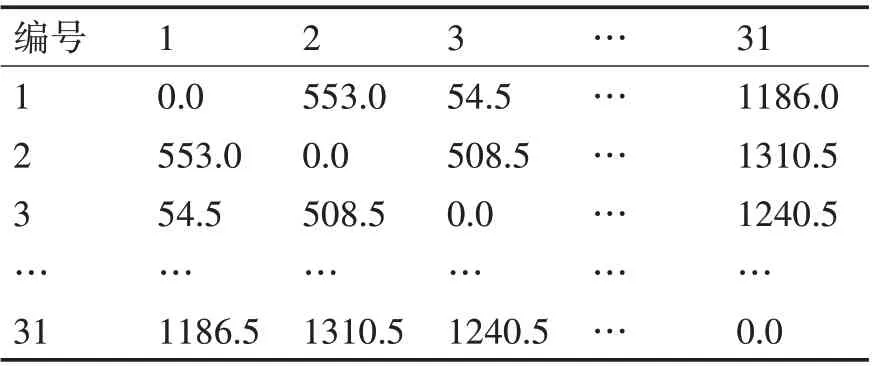
表2 城市间交通运算所需费用表

本实验将种群大小设置为200，最大遗传代数为1000，代沟为0.9，变异概率为0.05，对有年龄操作和无年龄操作分别进行5 次计算，变化曲线图见图2～7，其中图2 为有无年龄操作后的种群最优解所需费用变化曲线图，图3 为有无年龄操作后的种群平均所需费用变化曲线图，图4 为有年龄操作种群最优解所需费用变化曲线图，图5 为无年龄操作种群最优解所需费用变化曲线图，图6 为有年龄操作种群平均所需费用变化曲线图，图7 为无年龄操作种群平均所需费用变化曲线图。

图2 种群最优解所需费用变化曲线图

图3 种群平均所需费用变化曲线图

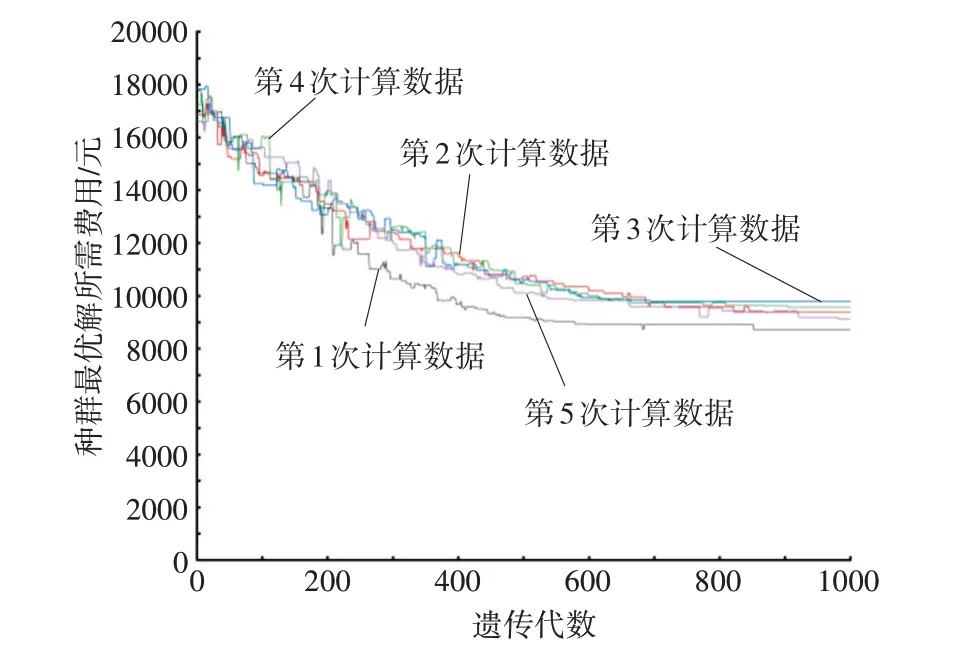
图4 有年龄操作种群最优解所需费用变化曲线图

图5 无年龄操作种群最优解所需费用变化曲线图

图6 有年龄操作种群平均所需费用变化曲线图

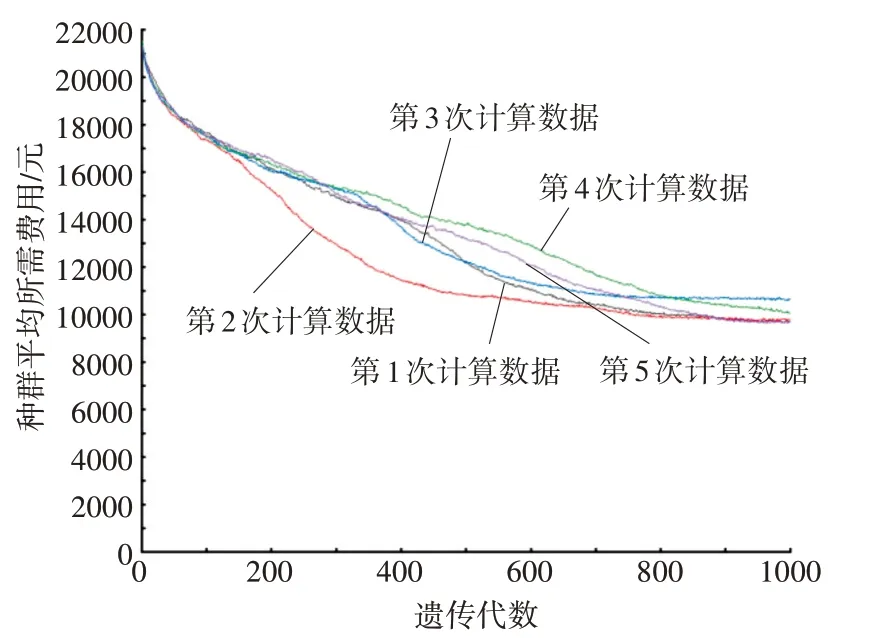
图7 无年龄操作种群平均所需费用变化曲线图

从图2～7 可以看出，对传统遗传算法添加年龄操作具有很好的可实践性，当参数设置相同的情况下，对有年龄操作和无年龄操作分别进行5 次计算，有年龄操作得到的最优巡回路径比无年龄操作得到的最优巡回路径更优，所需旅行总费用更低。当添加年龄操作，强制淘汰达到死亡年龄且适应能力高的优秀个体，可以有效避免种群的多样性受到破坏，使遗传算法过早地出现早熟和收敛现象。

表3为有年龄操作计算5次后的所需费用统计表，表4 为无年龄操作计算5 次后的所需费用统计表。

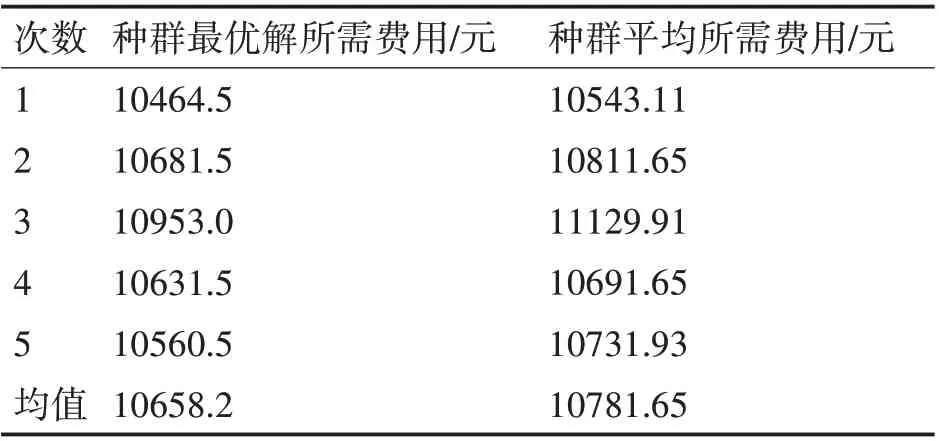
表3 有年龄操作计算5次费用统计表

表4 无年龄操作计算5次费用统计表

从表3和表4可以得到，进行年龄操作后，平均种群最优解所需费用比无年龄操作所得到的总费用消费更少，相应的种群平均所需费用也比无年龄操作所消费的总费用更少。由此可得，添加年龄操作，对于国内的旅行交通规划可以实现更好的巡回路径，能够为人们的旅行提供更优、更合理化的建议，节约旅行资金。

对各城市旅行解码前得到的最优路线为

解码后的最优路线为

上述最优路径所需总费用为10464.5 元，图8为最优解巡回路径图，图9 为文献［15］遗传算法所获得的最优巡回路径图。

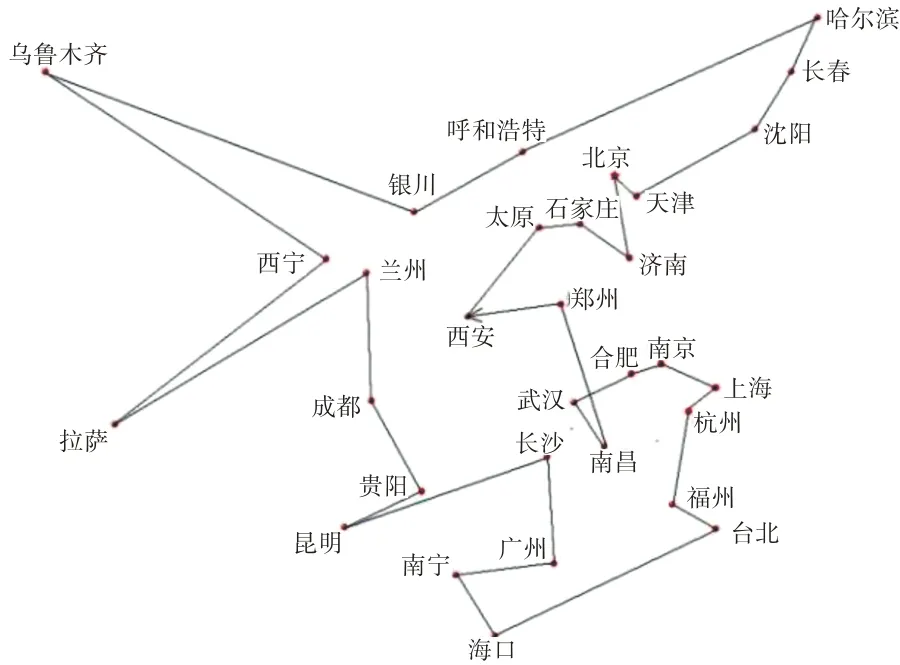
图8 最优解巡回路径图

图9 文献［15］遗传算法巡回路径图

将本文改进遗传算法所获得的最优巡回路线需要的总费用与文献［15］优化路径所需费用进行对比，结果见表5。

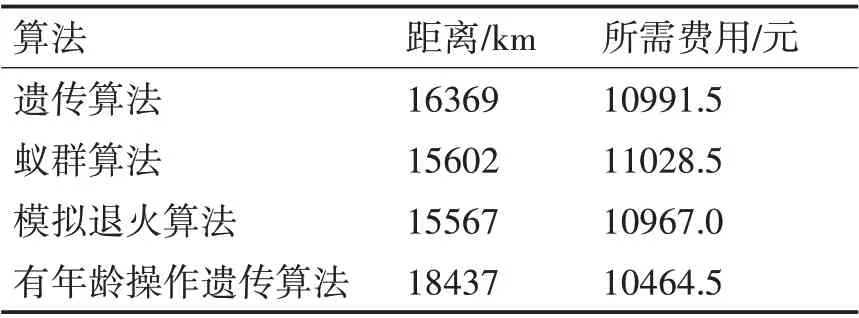
表5 与文献［15］优化路径所需费用对比表

如表5 所示，文献［15］利用遗传算法、蚁群算法和模拟退火算法所获得的优化路径全都比有年龄操作遗传算法优化的路径总距离少，但所需费用都更高，改进遗传算法获得最优路径的所需总费用比文献［15］三种算法所需费用分别省527 元、564元和502.5 元，为人们的外出旅行节约了一定的资金。

5 结语

对国内旅行外出进行旅行交通规划，可以为人们出行路线安排提供合理化的建议，使人们对出行安排进行理性分析，节约外出消费资金，做出更正确的路线规划和决策，满足了人们的精神文化追求和享受。在国内旅行交通规划研究中，对传统遗传算法中添加年龄操作相比无年龄操作遗传算法，能够更好地求得巡回路线最佳解，得到更优的旅行路线以及更少的所需费用，提供合理化的旅行线路图。改进遗传算法以所需费用为优化目标，可能会增加部分总距离，但是在限定的资金范围内，能够缓解经济压力，减轻成本负担，让出行更加的轻松享受。