化学平衡移动三判据整合的数学推导过程
2022-03-17侯保林耿晶晶宋秀丽
侯保林 耿晶晶 宋秀丽



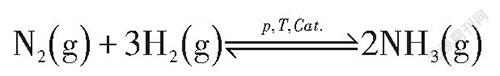
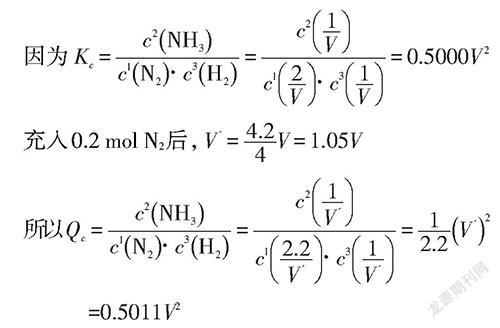
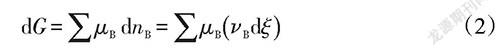
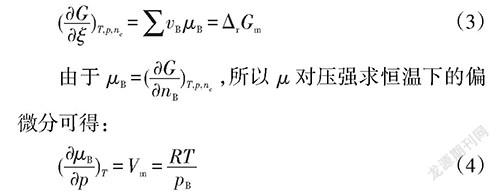


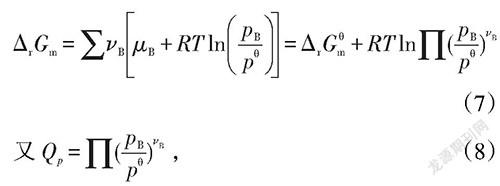

摘要:基于学生在学习彼此割裂的化学平衡移动三判据时存在明显的学困现象,针对吉布斯自由能变化ΔG与化学平衡常数K与浓度商Q的定量比较在当前课堂教学中等价性证明的欠缺,对吉布斯自由能变化与化学平衡常数的关系进行了数学推导。该推导解决了吉布斯自由能变化作为化学平衡移动的判据在课堂教学中过于突兀呈现的问题,为学生追求化学中蕴含的数学美提供了示范。
关键词:化学平衡移动;勒夏特列原理;化学平衡常数;复合判据
文章编号:1008-0546(2022)03x-0091-03 中图分类号:G632.41 文献标识码:B
doi:10.3969/j.issn.1008-0546.2022.03x.025
二十世纪最伟大的化学家之一鲍林(L. C. Paul ing)曾说过:“对勒夏特列原理了解之后,可以思考任何化学平衡的问题,并可以通过简单的论据对反应移动进行定性的解释。大部分人毕业后,可能忘记了所有与化学平衡有关的数学方程式,但還依旧能记住勒夏特列原理。”可以看出,鲍林对勒夏特列在化学初学者平衡观念建构方面所做的杰出推广,给予了充分的肯定[1]。
1884年,勒夏特列(H. L. Le Chatelier)发表了第一版化学平衡移动原理:一个稳定的化学平衡体系受到一种迫使它改变温度、压力、浓度的外力作用时,它的整体或者局部能够进行自我调节,并且自我调节引起的变化与外力所引起的变化相反。该表述较好地解释了工业生产中如何实现产率增长的问题。1888 年,基于对吉布斯(j.W.Gibbs)热力学理论的深入了解,勒夏特列在《矿业年鉴》上的一篇文章中做了更为精简和准确的表述:某一种均衡因素的每一次变化都会导致系统重新排列,重新排列使得所讨论的因素发生与原变化相反的变化,此即为今天大家所熟知的“勒夏特列原理”。
高中化学教材中,判定化学平衡移动方向时用到三个判据,分别是勒夏特列原理(本文认定为判据一,后文以此类推)、平衡常数K与浓度商Q的定量比较(判据二)及吉布斯自由能变化ΔG(判据三)。如何编排三个判据的学习顺序,各版教材存在差异,但并没有实质性的区别[2]。本研究有针对性地选择人教版(2019)选择性必修1《化学反应原理》展开讨论。
一、勒夏特列原理(判据一)的局限
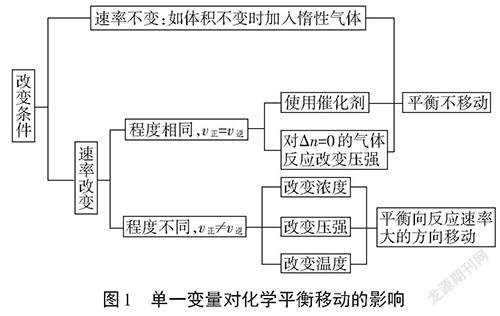
经过高中化学必修2的学习,学生已经具备初步的化学平衡观念,并且掌握了一定分析和解决化学平衡问题的技能。为了体验科学史上勒夏特列如何真实地利用平衡移动原理解决工业生产问题,该教材在第38页“科学史话”[3]栏目给出翔实的素材以开拓学生思维,引导学生化学史观和化学概念的自我构建。课堂观察发现,在学习如何应用单一变量确定平衡移动方向时,基本能做到较高的达成度。图1清晰地表明了诸多单一变量对化学平衡移动的影响。
多数学习情境中,从控制变量的角度出发,改变均相体系化学平衡的单一变量,并非“真单一变量”,而是“伪单一变量”,即多变量。为了解决多变量在教学实践中易造成与勒夏特列原理不相吻合的实际问题,提出定量判据使用的必要性预测结果。以合成氨平衡体系为例:
假定该合成氨反应在恒温恒压条件下进行,平衡时各组分物质的量分别为:n(N)=2 mol,n(H)=1 mol,n(NH)=1 mol。若充入0.2 mol N使原平衡被破坏,新平衡将向何处移动呢?按照勒夏特列原理(判据一)定性判定,多数学生会想当然地认为平衡向正反应方向移动;事实上,恒温恒压条件下,充入N势必会引起体系总体积的增大和体系中各组分分压的改变。因此在该平衡体系中充入氮气属于“伪单—变量”。此时,对于多变量影响平衡移动方向的判定,定性分析模型将不再适用,充分显示出勒夏特列原理(判据一)的局限,更适宜通过对比浓度商Q与化学平衡常数K的相对大小定量判定。具体的计算过程如下:
因为Q>K,所以平衡逆向移动,即向N分子数增多的方向移动。
通过运用化学平衡常数K与反应。的定量比较(判据二)巧妙地摆脱了勒夏特列原理(判据一)的局限,问题迎刃而解。
二、化学反应等温方程的推导
吉布斯自由能变化ΔG(判据三),即“ΔG=ΔHTΔS”,在高中化学教材中只占了极少的篇幅,学生学习后记住的仅仅是彼此割裂的抽象符号,呈现过于突兀和生硬。吉布斯自由能变化ΔG的意义并没有展开讨论,它与化学平衡常数K的关系亦未推导。学生的情感体验很难从物理量符号的意涵理解中获得升华。考虑到热力学平衡规律的整合作用,在使用判据一、判据二的同时,引入判据三对化学平衡移动进行判定则更为可靠。
要理顺ΔG与K的数学关系,必然需要学生具有一定的微积分基础。化学平衡移动主题的课程在高二上学期展开,而数学上针对积分知识的学习,大多安排在高二下学期,这就从客观上设置了ΔG与K的数学关系推导的跨学科整合门槛,提高了同化的难度。
要成功推导ΔG与K的数学关系,通常情况下,化学势μ是一个无法避开的物理量。当初,吉布斯提出化学势μ为了统一U、G、A、H四个热力学函数、使其等价提供重要支撑[4](当然,等价的工作是后来的学者规范和统一的,当时发明这些热力学符号的科学家并非有意为之);若在高二年级初次学习时贸然引入μ,而学生缺乏对μ的学习支架,势必会导致学生对该内容采取敬而远之的学习态度。
然而经过高二年级一学年的数学知识储备,学生已经具备基本的积分运算能力。此时开展三个判据的整合推导,不仅能体现对数学符号的掌握,还能够巧妙迁移到化学平衡移动的判据整合过程中。
公式ΔG=-RTlnK+RTlnQ中,包含了判据二与判据三两个定量判据存在的内在逻辑,对化学平衡移动的学习,有根本性的指导作用。所以,该公式的推导具有一定的重要性和必要性。
因此,受到傅雪青等[5]数学建模的启发,用微积分整合三个化学平衡移动的判据,推导ΔG与K的数学关系,使判据二和判据三的数学逻辑关系更加清晰。
1.含μ的推导过程
通常情况下,推导ΔG与K的关系,采用的是引入μ的方法。
非体积功为零的多组分吉布斯函数全微分表达推导如下:
dG=-SdT+Vdp+∑μdn (1)
化学平衡体系中,恒温恒压条件下,非体积功为零时的多组分吉布斯函数全微分式如下:
求吉布斯函数对反应进度偏微分可得:
对其积分可得:
进一步可得:
左右乘以对应的计量系数v可得:
代入上式可得:
通过桥连公式(10),可以得到图2,将判据二与判据三紧密关联起来,不仅表明了化学平衡移动判据二与判据三的等价性,而且对学生化学平衡观的完整建构具有更加专业的指导性。
2.不含μ的推导过程
对于反应aA(g)+bB(g)⇌cC(g)+dD(g),若不引入μ,单纯采用数学积分的办法推导ΔG与K的关系,具体过程如下:
假定该反应存在恒温恒容时两种不同的压强状态。反应处于标准态p时,相应化学平衡常数
当恒温恒压条件下,反应进度为1 mol时,有:
公式(13)即为公式(10)。
通过比较可知,采用引入μ的方法推导ΔG与K的关系,会给学生带来学习难度、深度和梯度的增加。而在不考虑热力学意义的前提下,不引入μ,单纯采用数学积分的办法推导ΔG与K的关系,依靠积分做差的方法,获得比较理想的桥连公式,将大大提高化学平衡观的功能性附着。
三、结论与启示
通過比较在化学势μ引入和不引入两种不同的条件下,运用积分详细推导ΔG与K的关系,表明了化学平衡移动判据二与判据三的等价性,将化学平衡移动三判据有机整合,解决了吉布斯自由能变化作为化学平衡移动的判据在课堂教学中过于突兀呈现的问题。
勒夏特列原理巧妙地展示其对化学平衡移动理论的强大推广功能,更加系统的化学平衡观的形成、理解及应用则需要严谨的数学语言予以阐释。所以中学化学教学应努力借鉴STEAM课程[6],关注其他学科的教学进度,主动与其他学科教师沟通和交流,有利于为学生的学习开拓思路。同时,为了提升学生学科素养和学科交叉的兴趣,教师应积极鼓励学生尝试用更规范的数学模型对化学现象进行高阶认知,辅助学生将数学能力拓展到化学理论学习中。
参考文献
[1]L.C Pauling. College Chemistry,3rd ed.[M]. Freeman,San Francisco,CA,1964:437-438.
[2]刘懿瑾.基于化学平衡的人教版与鲁科版在选修教材化学反应速率、限度、方向内容的研究[D].武汉:华中师范大学,2016.
[3]人民教育出版社,课程教材研究所,化学课程教材研究开发中心.普通高中教科书(化学选择性必修1)[M].北京:人民教育出版社,2019:38.
[4]殷开梁.物理化学中化学势的含义及应用详解[J].化学教育(中英文),2018,39(18):18-23.
[5]傅雪青,方向东.可以用数学方法解决的几个高中化学问题[J].化学教育(中英文),2020,41(13):101-105.
[6]张辉蓉,盛雅琦,念创.我国STEAM教育改革的阻力与消解.中国教育科学(中英文),2021,4(2):76-85.
2452501705395
