基于启发式规则的物流配送车辆排班优化

李栓子 施国洪

摘要：针对 A 物流公司不同车型的物流车辆配送路径复杂，且每辆车每天可以执行多条线路任务的特点，设计了两种启发式规则求解物流车辆排班任务。首先，对该物流公司存在的问题进行了分析;其次，根据约束条件建立了目标函数为总行驶路程的数学模型，设计了启发式规则1用于进行任务的安排，并使用 A 公司的物流数据Part1作为算例进行数据仿真，通过对仿真结果的分析，在启发式规则1的基础上进行改进设计了启发式规则2;最后，将两种启发式规则的仿真结果进行对比，发现启发式规则2的性能更佳也更稳定，该结论进一步验证了启发式规则解决物流配送车辆排班任务的有效性和可行性。

关键词：启发式规则;车辆排班;物流配送;路径规划

一、引言

随着互联网和大数据等信息化技术的发展，企业间的竞争日益激烈。最初，企业通过降低产品的成本来提高企业的经济效益，但原材料价格和劳动力价格的上涨使得企业难以在生产上节省更多成本。如今，企业纷纷将目光转向自身物流体系的成本，而物流成本中有很大一部分责任是由运输承担的，因此，运输的成本与效率成为企业越来越关注的问题。

早在1959年，Dantzig和Ramser就提出了车辆路线问题（Vehicle Routing Problem），即如何配置车辆类型和数目，如何为各车辆安排一组最优或者是较优的路线，使得在满足所有约束条件的情况下总的代价最小。带时间窗约束的车辆路径问题（Vehicle Routing Problem With Time Window Constraints）是车辆路径问题（VRP）的拓展与延伸，广泛应用于资源配置和物流运输等方面。Aldair Alvarez和Pedro Munari采用了混合算法解决 VRPTW 问题，算法在分支-定价-定界算法中使用两种元启发式算法产生可行解。K.K.H.Ng等提出了一种多聚居地人工蜂群算法来解决速度时变的VRPTW 问题，并验证了该算法优于其它的人工蜂群算法。Duygu Tas 等运用了禁忌搜索算法和自适应大规模邻域搜索算法求解该问题，并验证了算法在实际环境中的有效性。Sophie N.Parragh和Jean-Franois Cordeau分别采用了分支-定价算法和自适应大规模邻域搜索算法解决带时间窗的卡车拖车路径优化问题。Sumaiya Iqbal等提出了一种结合了多步局部搜索和人工蜂群算法的混合算法，不过没有验证算法有效性。

目前求解 VRPTW 的算法可以分为精确算法和元启发式算法两类。精确算法（Accurately Arithmetic）在求解规模较小的路径优化问题时，能够在可承受的空间与时间消耗下得到精确解。但是配送路径优化问题属于NP问题，实际求解过程中问题的规模较大，使用精确算法所消耗的空间和时间成本都比较大。而启发式算法（Heuristics）不管是求解小规模的问题还是大规模的问题，都能在一定的范围和较短时间内给出最优解。因此，目前相关领域的专家以及研究人员，对于求解算法的主要研究方向是启发式算法。

从文献可知启发式算法可以归为启发式规则和元启发式算法两类，现有的研究大多专注于元启发式算法。陈小潘等在校车路径规划中首次设计了针对校车路径问题（SDSBRP）的元启发式求解算法，该算法首先构造初始可行解，然后在模拟退火算法框架下，引入站点需求拆分的邻域搜索算子进行迭代搜索，逐步改善解的质量。赵晶等通过应用传统启发式规则的第一和第二规则并与随机方法相结合的方式，解决了卡车装配线平衡问题。唐勇等提出一种新型遗传模拟退火算法求解VRPTW问题。张建同等考虑不同时间段车辆行驶速度不同的情况，提出一种变邻域模拟退火算法求解速度时变的VRPTW问题。但是针对具体物流企业车辆配送路径复杂、排班任务繁重的问题多数研究并未涉及。

鑒于此，本文从实际问题出发，考虑物流公司不同车型的物流车辆配送路径复杂且每辆车可以执行多条线路任务的特点，采用两种启发式规则来解决物流配送车辆排班问题，为企业优化物流配送路径，节省企业物流成本进而提升企业的市场竞争力具有一定的理论和现实意义。

二、问题描述及数学模型

（一）问题描述

本文以 A 物流公司为原型，对该公司的物流配送车辆排班任务进行研究，该公司的配送任务中，有成千上万条不同车型运行的线路，随着线路数量的增加，依赖人工进行线路的规划已经难以满足整体规模和复杂度。因此如何运用新的技术规划路线，使得车辆的利用率得到提升，网络运营成本降低是我们需要探索的方向。与VRPTW相比，本次研究的主要区别在于对于相同的两个节点可能存在多次访问任务。该物流公司物流配送方面问题可以描述为，给定一系列有效运输任务（起止地点、起止时间）的情况下，将运输任务组合成车辆行驶的线路，在满足以下约束的条件下，总的行驶里程最少。其中约束为以下三条：

约束1：线路的起止点必须相同，即车辆必须回到原点;线路可以由有效运输任务和空驶任务构成，线路中的每段任务必须首尾相接，即前一段任务的结束点是下一段任务的起点。

约束2：一条线路认为分配给一辆车执行，因此在时间上可行，即不能出现时间上的冲突和重叠。

约束3：考虑到司机的行驶和线路的稳定性，线路的运行时间不能超过48个小时，线路段数不能超过4段。

1.对约束1的分析

通过对以上问题描述和约束的理解，可以将该问题归纳为目标函数为总行驶路程最短的VRPTW问题。对于约束1，路线必须首尾相连，但可以出现空驶任务，则可能出现情况3。

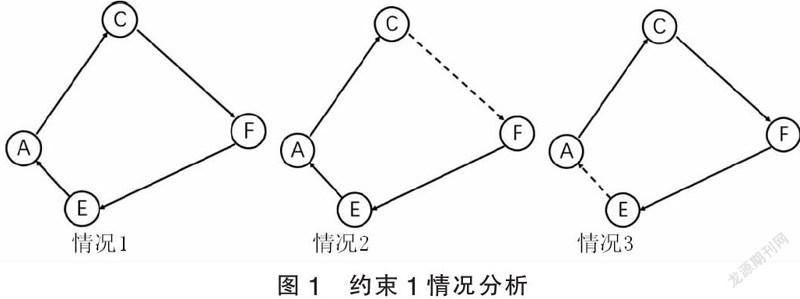
情况1：如图1的a子图所示，所有的任务都为有效任务，且首尾相连。

情况2：如图1的b子图所示，该线路没有符合条件的后续任务，存在空驶任务，且空驶任务在中间，C→F为空驶任务。

情况3：如图1的c子图所示，该线路没有符合条件的后续任务，且空驶任务在最后，三段任务完成后，第一段任务的起点不是第三段任务的终点，因此第四段任务为E→A。

2.对约束2的分析

同一条线路中，前一段任务的结束时间必须小于等于后一段任务的开始时间，若在满足其余约束的情况下，没有符合条件的后续任务，则该条线路结束。

3.对约束3的分析

第一段任务的起始时间与最后一段任务的结束时间之差必须小于48小时，通过对物流数据Part1的分析选取具有代表性的数据，如表1所示（本文将全天0～24小时折算为0～1439分，表1中的出发时间及到达时间均为相对于0点的分钟数），最早的出发时间为9，而最晚的到达时间为第二天的159，间隔时间为1590min，即26.5h，因此在求解过程中可以忽略48小时的限制。

本次研究没有一个对总行驶路程的具体约束，因此在求解过程中没法判断所设计算法的效果，但是通过对Part1数据进行分析不难发现，总行驶里程存在一个隐含的上下界限可以验证算法的效果。

对于上界，在任务分配时，最差的情况就是每一辆车辆行驶一个任务，而由于存在车辆必须回到原点的约束，每辆车辆在行驶完任务后需要空驶回原点，因此总行驶路程的上界为所有任务距离之和的两倍。

对于下界，考虑一个理想状态，所有的任务都可以以首尾相连的方式分配给车辆，即不存在空驶任务，因此总行驶路程的下界为所有任务距离之和。

如图2所示，假设存在10个任务，最佳方案即总行驶路程最短为不存在空驶任务，车辆数量为3辆，最差方案即总行驶路程最长为一个任务由一辆车执行，车辆数量为10辆。从图2中可以看出，最差方案的总行驶路程是最佳方案的两倍。

通过对Part1的341段任务的距离计算，可以得到理论最短总行程为22177公里，最长总行程为44354公里。

（二）数学模型

问题可描述为：已知一个车辆的集合K，节点集合N，以及任务集合G。其中车辆集合V为1，2，…，K;节点集合N为1，2，…，n;任务集合G表示为1，2，…，g;对于每一任务i，任务的时间约束为[si，ei]，lsi表示任务i的起始点，lei表示任务i的终止点，di表示任务i的行驶里程。车辆必须在早于tsi的时间内到达任务i的起始点lsi，直至所有的任务都被访问，求解满足约束下的最短车辆行驶路程。

该问题的数学模型可以表示为如下：

定义决策变量如下：

Xijk1;若车辆k从任务i到任务j0;若车辆k没有从任务i到任务j（8）

Yijk1;若车辆k从空驶任务i到任务j0;若车辆k没有从空驶任务i到任務j（9）

Zijk1;若任务j为车辆k行驶任务i的后续任务0;若任务j不为车辆k行驶任务i的后续任务（10）

其中，式（1）为目标函数，表示总里程，包含有效任务的总里程和空驶任务的总里程;式（2）为每辆车的线路段数不能超过4段;式（3）为每辆车的线路运行时间不能超过48小时;式（4）为每条线路的前一段任务的结束时间小于等于后一段任务的开始时间;式（5）为每条线路的前一段任务的结束点为后一段任务的开始点;式（6）为每个有效任务都要被访问到;式（7）为每个有效任务只能被访问一次;式（8）为0～1变量，若车辆k从任务i到任务j，则为1，否则为0;式（9）为0～1变量，若车辆从空驶任务i到任务j，则为1，否则为0;式（10）为0～1变量，若任务j为车辆k行驶任务i的后续任务，则为1，否则为0。

三、启发式规则1设计

针对所研究问题的特点，设计了一种启发式规则进行求解。同时采用Matlab 2014a进行编程，并在Windows7 Intel（R） Core（TM） i5-3337U，CPU1.8GHz，内存4GB，64位操作系统的计算机上运行。算法的参数设置为：种群大小50 迭代次数为200 代。

（一）启发式规则1流程设计

启发式规则1流程图见图3，具体步骤见下列。

Step1：初始化参数车辆号car=1，已访问任务visited =0，任务总量num。

Step2：选择第car辆的第一个任务。从剩余任务中选取出发时间最早的任务为第car辆的第一个任务，若有多个，则随机选取，visited = visited + 1;若visited = num，则算法结束。

Step3：选择第car辆的后续任务。筛选出符合条件的任务点（筛选规则见前文），从中任选一个，visited = visited + 1，若visited = num， 则算法结束，否则转向Step3;若不存在符合条件的任务，则car = car + 1，并返回Step2。

（二）筛选规则

车辆在选定第一个任务后，选择后续任务时，需要根据约束条件进行筛选，筛选规则如下：

规则1：若该任务为第四段任务，则需要保证第三段任务的终点为该任务的起点，该任务的终点为第一段任务的起点;该任务的出发时间需大于等于第三段任务的结束时间;该任务的结束时间减去第一段任务的开始时间需要小于等于48小时。

规则2：若该任务为第二/三段任务，则需要保证前一段任务的终点为该任务的起点;该任务的出发时间需大于等于前一段任务的结束时间;该任务的结束时间减去第一段任务的开始时间需要小于等于48小时。

（三）结果分析

通过Matlab进行代码实现，算法的参数设置为：种群大小为50 迭代次数为200 代。对数据样例_Part1运行10次，得到如表2所示的总行驶路程和所需车辆数量。

其中，总行驶路程最短为29124km，车辆的行驶路线见表3，收敛曲线如图4所示。

四、启发式规则2设计

通过对启发式规则1的求解结果进行分析，发现前面的车辆都可以进行3～4段有效线路段数，但到了后期的车辆基本只有1～2段有效线路段数。那么对于后期的车辆来说，基本都需要在最后行驶一段空驶路程。从目标函数为总行驶路程角度考虑，如果后期的车辆空驶路程都尽可能小，那么就能够减小最后的总行驶路程。

（一）启发式规则2流程设计

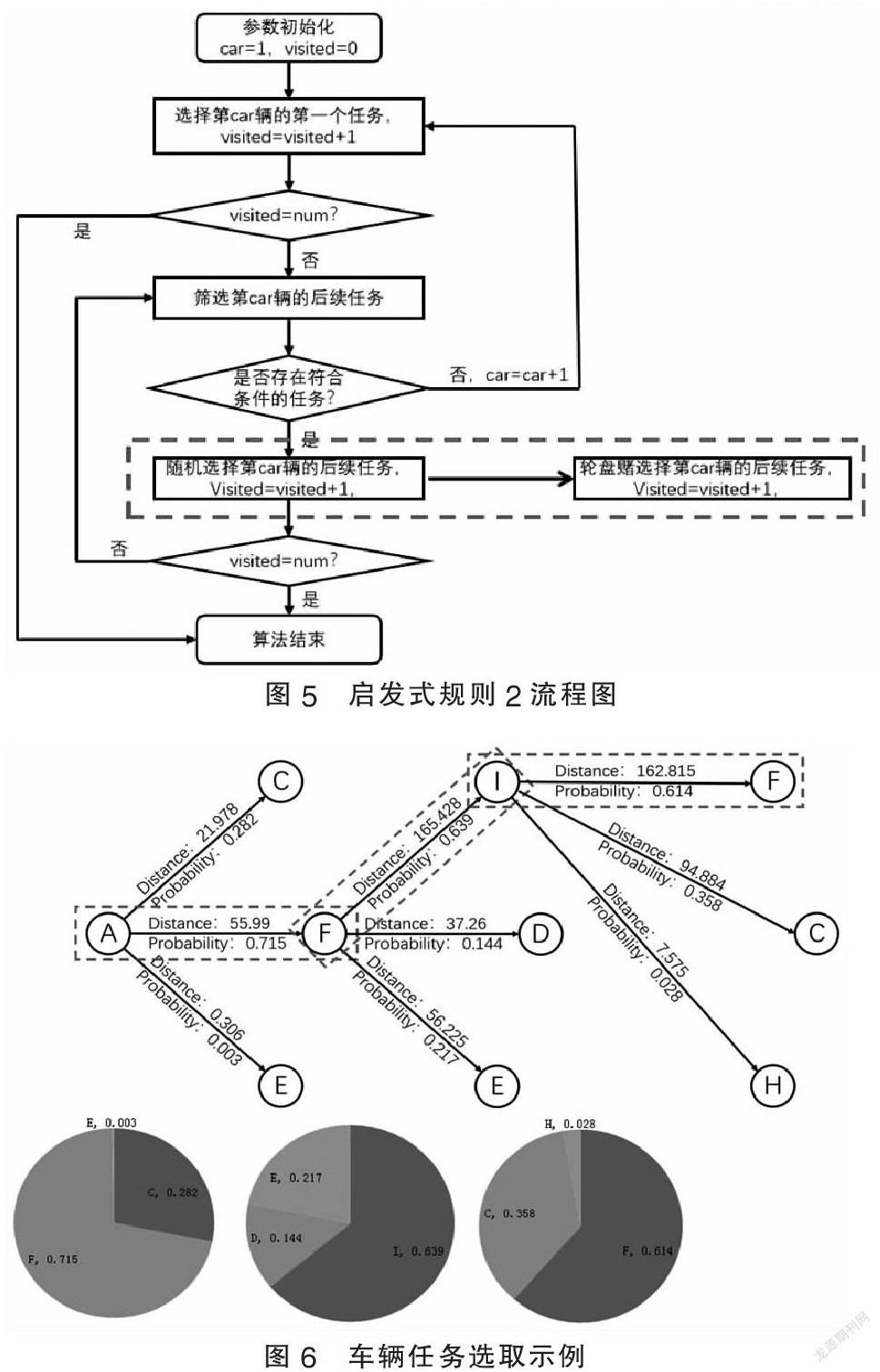
流程图如图5所示，与启发式规则1相比，算法流程大致相同，只是在Step3中选择车辆的后续任务发生改变，启发式规则1为从符合条件的任务点中随机选择，启发式规则2为通过轮盘赌的形式选择后续任务。其中轮盘赌的概率与任务的距离成正比，任务的距离越大，被选中的概率越大。

如图6所示，为某一车辆的后续三段任务的选取，假设A的后续任务点为C、F、E，根据相应的距离A-C：21.978，A-F：55.99，A-E：0.306，被选中的概率分别为0.282、0.715、0.003，其轮盘赌概率区间分别为[0，0.282]、[0.282，0.997]、[0.997，1]，随机rand值为0.56，因此，A的后续任务点为F。依次类推该车辆最终的后续路线为A→F→I→F。

（二）结果分析

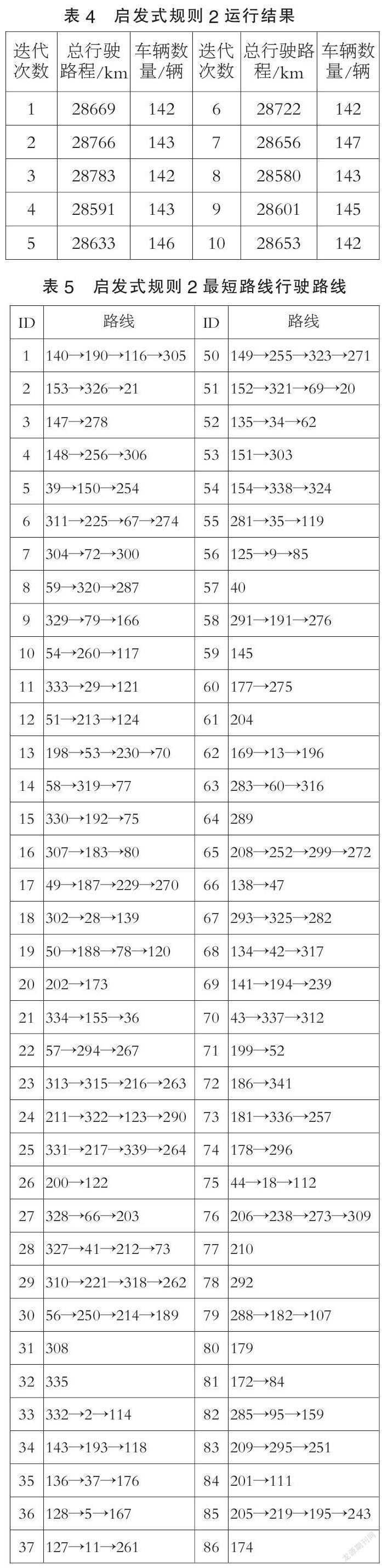
通过Matlab进行代码实现，算法的参数设置为：种群大小为50 迭代次数为200 代。对数据样例_Part1运行10次，得到如表4所示的总行驶路程和所需车辆数量。

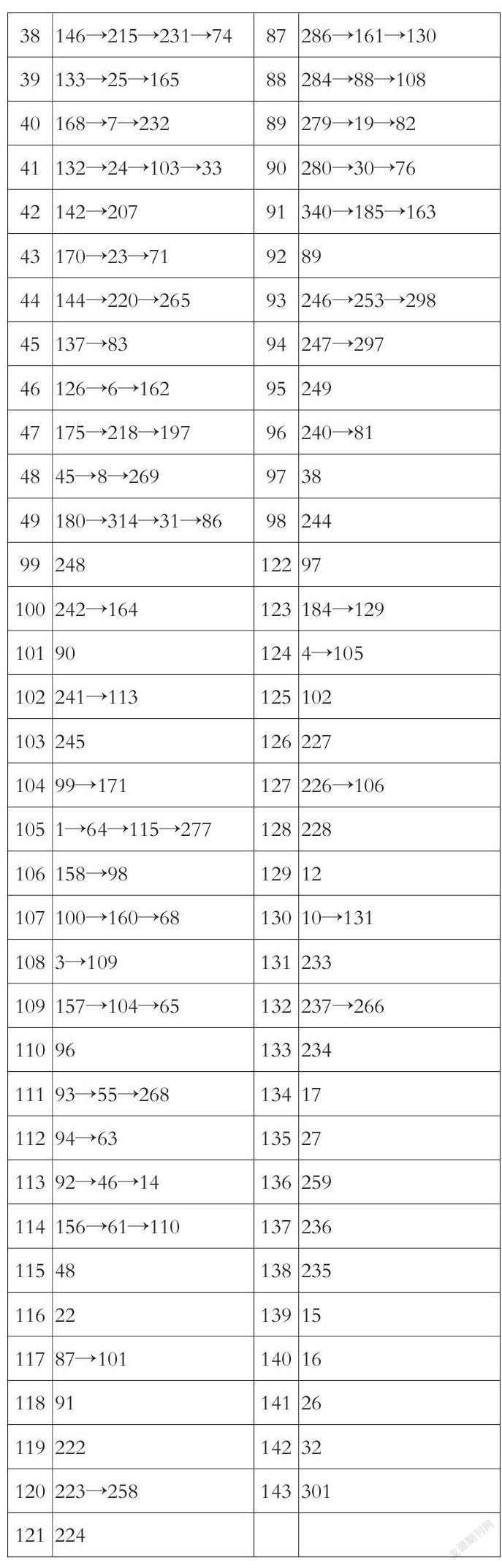
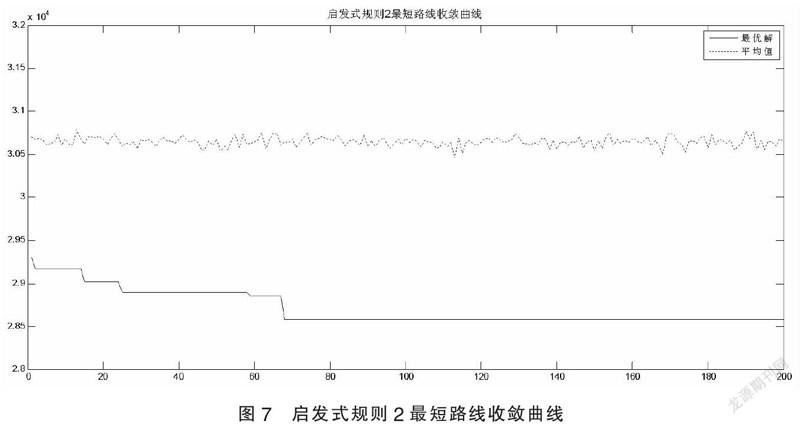
其中，总行驶路程最短为28580km，车辆的行驶路线见表5，收敛曲线如图7所示。

五、启发式规则对比分析

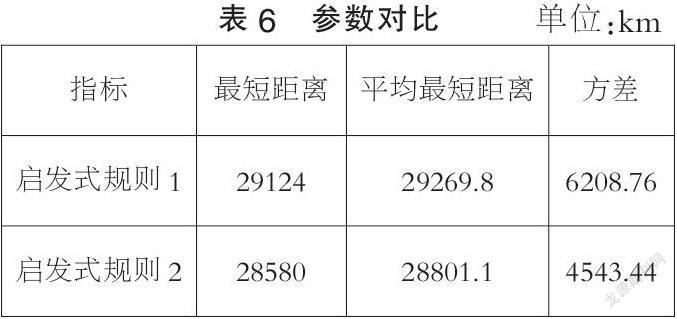
通过对比两种启发式规则的10次求解结果以及两种启发式规则的最短路线收敛曲线，可以得到如表6的结论，与启发式规则1相比，启发式规则2的最短距离降低544km，平均最短距离降低468.7km，方差也更小，因此启发式规则2的性能更佳，也更稳定。

六、结论

本文将启发式规则引入物流配送的车辆排班问题中，根据约束条件，建立了目标函数为总行驶路程的数学模型，并使用A公司的真实物流数据作为算例进行数据仿真，通过研究结果可以发现该研究将会降低车辆的行驶距离，这就意味着将会大大节约运输所带来的成本，从而使问题更具有实际意义。但是本文所提出的启发式规则是基于A物流公司问题本身的特点设计的，首先采用启发式规则能更好的搜索最优解，其次，通过启发式规则求解问题只需要很少的求解时间。但是本文的美中不足在于没有采用固有的元启发式算法对问题进行求解，且所设计的两种启发式规则还有很大的改进空间，例如车辆初始任务的选取可以设计一些规则，而不是选择开始时间最早的任务，这样将会增加求解空间的规模。进一步的研究可以使用元启发式算法求解该问题与其进行对比。

参考文献：

[1]Dantzig G.and Ramser J.The Truck Dispatching Problem[J].Management Science，1959，6（01）：80-91.

[2]Aldair Alvarez，Pedro Munari.An exact hybrid method for the vehicle routing problem with time windows and multiple deliverymen[J].Computers & Operations Research，2017，7（83）：1-12.

[3]Ng K K H，Lee C K M，Zhang S Z，Kan Wu，William Ho.A multiple colonies artificial bee colony algorithm for a capacitated vehicle routing problem and re-routing strategies under time-dependent traffic congestion [J].Computers & Industrial Engineering，2017，7（109）：151-168.

[4]Duygu Tas，Nico Dellaerta，Tom van Woensel，Tonde Kok.The time-dependent vehicle routing problem with soft time windows and stochastic travel times[J].Transportation Research Part C：Emerging Technologies，2014，11（48）：66-83.

[5]SophieN.Parragh，JeanFranois Cor-deau.Branch-and-price and adaptive large neighborhood search for the truck and trailer routing problem with time windows[J].Computers & Operations Research，2017，7（83）：28-44.

[6]Sumaiya Iqbal M，Kaykobad Sohel Rahman M.Solving the multi-objective vehicle routing problem with soft time windows with the help of bees[J].Swarm and Evolutionary Computation，2015，10（24）：50-64.

[7]陳印，徐红梅.混合算法在车辆路径优化问题中的应用[J].计算机仿真，2012（05）：356-359.

[8]胡纯德，祝延军，高随祥.基于人工免疫算法和蚁群算法求解旅行商问题[J].计算机工程与应用，2004（34）：60.

[9]陈小潘，孔云峰，郑泰皓，等.需求可拆分校车路径问题的元启发式算法[J].计算机科学，2016，43（10）：234-241+261.

[10]赵晶，吴翠红，王昭宇.应用元启发式算法解决特殊约束的装配线平衡问题[J].湖北农机化，2019（19）：128-130.

[11]唐勇，刘峰涛.新型遗传模拟退火算法求解带VRPTW问题[J].计算机工程与应用，2006，42（07）：7-9.

[12]张建同，丁烨.变邻域模拟退火算法求解速度时变的VRPTW问题[J].运筹与管理，2019，28（11）：77-84.

（作者单位：江苏大学管理学院）

1052500511354