基于拓扑聚合的输电断面辨识方法与断面传输极限的研究

张大波，王博欣，郭怀新，储著伟，杨贺钧，马英浩

基于拓扑聚合的输电断面辨识方法与断面传输极限的研究

张大波，王博欣，郭怀新，储著伟，杨贺钧，马英浩

(新能源利用与节能安徽省重点实验室(合肥工业大学)，安徽 合肥 230009)

国内外多次发生的大停电事故表明输电断面是大规模互联电网的薄弱环节。快速搜索出电网关键输电断面并计算出断面极限传输功率，有利于调度部门及时调整运行方式，避免电网发生大面积停电事故。提出利用电网拓扑聚合算法对电网关键输电断面进行搜索。通过对电网邻接矩阵进行简单的矩阵变换操作，将拓扑中临近节点聚合到邻接矩阵的主对角线附近。直接在变换后的邻接矩阵上对电网输电断面进行快速搜索，然后通过潮流分布因子来辨识关键输电断面。利用磷虾群优化算法构造电网关键输电断面极限传输功率的优化模型，准确计算断面极限传输功率。IEEE14节点系统和IEEE39节点测试系统验证了所提方法的有效性。

关键输电断面；邻接矩阵；拓扑聚合；磷虾群优化算法；极限传输功率

0 引言

具有间歇性、随机性的新能源大规模接入电网，使得电网传输的功率波动频繁。随机性故障与计划性检修相互叠加，使得电网拓扑结构不断变化，电网运行模式复杂多变。准确识别电网中的关键输电断面(Key Transmission Section, KTS)，并计算其极限传输功率，对保障电网安全稳定运行具有重要意义[1-3]。

关于输电断面的搜索方法广受关注。文献[4-5]基于最短路径法辨识输电断面，采用背离路径法或改进的Dijkstra法搜索前K最短路径，但是过度依赖过载支路的选取。文献[6]采用遍历算法搜索关键输电断面，但遍历算法属于典型的NP问题，其计算时间随着电网规模的扩大呈指数增长。文献[7-9]采用了地理分区、边界优化方法以及AP聚类的方法，通过安全裕度指标确定关键输电断面，但这类方法难以对区内支路进行搜索，分区内部网络拓扑的特性被消除，可能导致关键输电断面遗漏。针对遍历类算法搜索输电断面导致计算速度慢以及采用电网预先分区的方法导致输电断面遗漏的问题，基于拓扑聚合的输电断面搜索算法[10-11]，将电网拓扑生成的邻接矩阵通过简单的矩阵变换转换为拓扑聚合矩阵，直接在拓扑聚合矩阵上实现电网分区的划分并搜索关键输电断面，实现计算速度与精度的同时提升。

在线计算输电断面极限传输功率可让调度员掌握电网运行边界，并根据传输的功率及时做出调整。计算极限传输功率的方法有连续潮流法[12-14]、最优潮流法[15]等。连续潮流法研究极限传输功率的原理简单，但迭代过程复杂，计算结果精度不足，具有很大的保守性。传统的最优潮流(Optimal Power Flow, OPF)法要求目标函数可微，存在“维数灾”和计算时间长等问题。近年来智能优化算法在非线性规划问题中的应用日趋增多，对约束条件有很强的处理能力，对上述计算输电断面极限传输功率出现的精度不足、计算时间过长、“维数灾”等问题取得了较好的效果[16-18]。但是电网关键输电断面极限传输功率的搜索空间巨大，如何在巨大的搜索空间内寻找全局最优解是一个挑战，传统的智能优化算法容易陷入局部最优，无法让调度员掌握电网运行边界，从而可能导致输电断面重载甚至过载，导致大面积停电事故。近年新提出的磷虾群优化算法(KHA)性能优异，文献[19-20]在标准测试函数上将KHA与多个传统优化算法进行对比，以最优适应度、时间处理、收敛性能为标准，验证了KHA在性能上优于传统优化算法，KHA采用随机搜索方向替代函数梯度方向，在搜索空间内非线性优化性能强，具有高度的并行性和鲁棒性，相比于传统智能优化算法，具备更快的收敛速度和优秀的全局收敛能力，因此更适用于输电断面极限传输功率的优化求解。

本文研究以拓扑聚合算法构造新的邻接矩阵为基础，直接在变换后的拓扑聚合矩阵上实现电网分区和输电断面的快速准确搜索；基于最优潮流构造关键输电断面极限传输功率的数学模型，以断面线路传输的有功潮流为目标函数，采用磷虾群算法进行优化计算，实现调度人员在线快速搜索关键输电断面并掌握电网运行边界，防止线路过载。

1 基于拓扑聚合算法的输电断面搜索

1.1 关键输电断面的定义

根据国内外专家对输电断面特征的探讨与总结，定义输电断面为：在某一基态潮流下，有功潮流方向一致，连接两个连通的电气区域，具有割集性质的一组输电线路的集合[10]。

在电力调度中，更关注对电网安全稳定运行有着重大影响的输电断面。定义关键输电断面为：某输电断面内，如果任意一条线路故障断开后，导致该断面内剩余线路潮流急剧增加，则将该输电断面称为关键输电断面[6]。

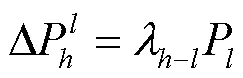
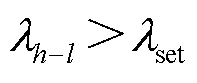
1.2 拓扑聚合算法

输电断面的搜索是否准确取决于电网分区的准确性。以14节点系统为例，如图1所示，按照节点编号顺序可以得到如图2所示的邻接矩阵[24]。为形象说明各节点在邻接矩阵中的拓扑关系，矩阵元素值为1的部分用黑色方块表示，矩阵元素值为0的部分用白色方块表示，可以直观地看出各节点编号没有考虑节点间的拓扑关系，导致矩阵中值为1的元素分布是无规律的，难以直接在矩阵上进行电网分区。如果有一种算法可以通过交换节点编号的方式将图2所示的邻接矩阵转换为图3所示的矩阵，人为将各节点按照图1拓扑结构由近及远的原则排列，就可以在矩阵上实现电网的分区。通过观察矩阵的元素分布情况，矩阵中值为1的元素都聚合在主对角线附近。

根据这一思想，本文提出拓扑聚合算法，通过定义距离指标对邻接矩阵进行简单的行列变换运算。行列变换操作(v↔v)是指将编号为v的节点所在行和列与节点v所在行和列分别进行互换，操作过程如图4所示，将矩阵中值为1的元素聚合到主对角线附近，实现矩阵中各元素按照彼此间拓扑关系和节点所在区域的相互联系聚合在一起。将通过行列变换运算得到的矩阵称为拓扑聚合矩阵。

邻接矩阵具有对称性，其主对角线上的元素下标和相等[21]。为使邻接矩阵中值为1的元素向主对角线聚合，定义距离指标为

对于图1所示的14节点系统，根据其拓扑结构对图2的邻接矩阵进行拓扑聚合后，邻接矩阵中节点的排列顺序发生了变化，得到图3所示的拓扑聚合矩阵。与原始的邻接矩阵相比，拓扑聚合矩阵体现了电网拓扑结构的特性，为在矩阵上实现电网的分区和输电断面的搜索提供了可能。

图1 14节点系统拓扑图

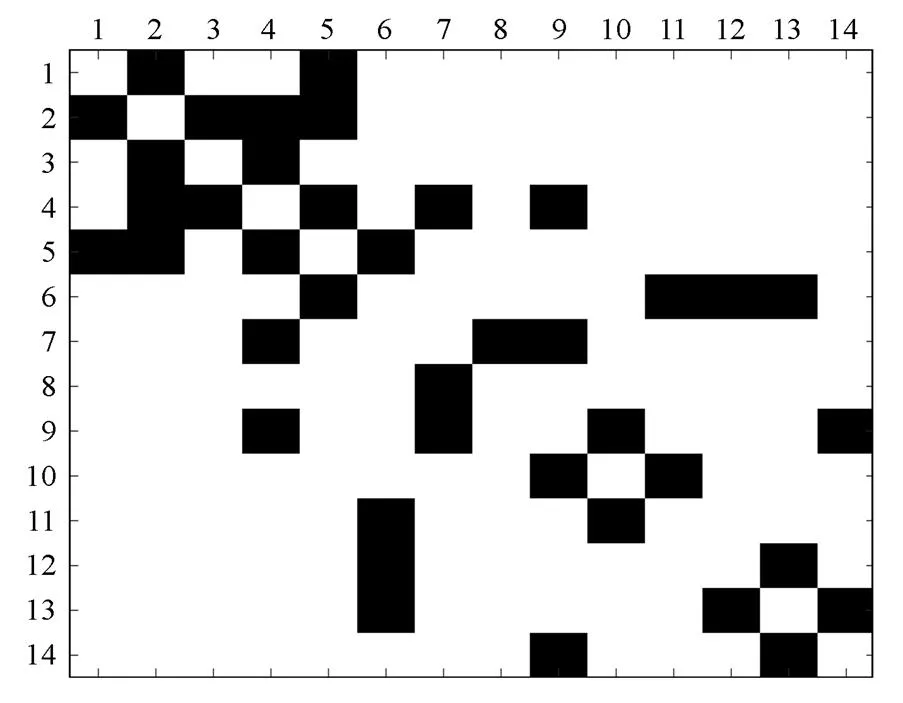
图2 14节点系统拓扑的邻接矩阵A

图3 14节点系统的拓扑聚合矩阵B

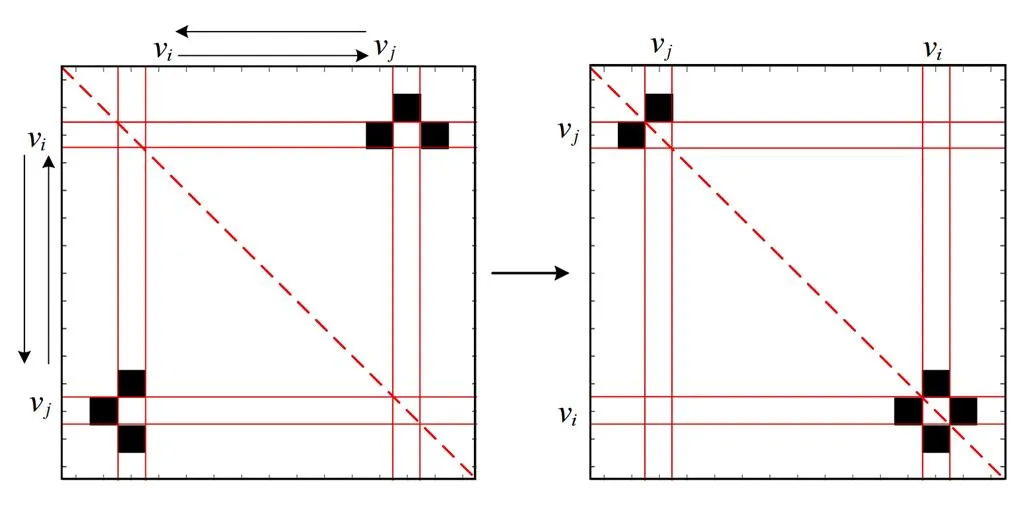
图4 节点vi和vj执行交换操作示意图

1.3 关键输电断面的搜索方法

通过拓扑聚合算法，邻接矩阵中节点的排列顺序发生变化。从图3可以看出，新的节点排列顺序={1,3,2,5,4,7,8,9,10,14,11,6,13,12}，拓扑结构中距离相近的节点聚合到拓扑聚合矩阵的主对角线附近，可以直观地在矩阵上划分3个电网分区Area以及对应的联络线子矩阵。节点集合{1,3,2,5,4}组成的区域被划分为电网分区Area1，Area1的输电断面是子矩阵1内包含的联络线，即={5-6,4-9,4-7}。同理得到矩阵内其他电网分区和对应的对外联络线。按照拓扑聚合矩阵中节点的排列顺序，依次搜索拓扑结构中所有电网分区，每个分区的输电断面为该分区对应子矩阵内的联络线。每个分区对应的子矩阵是指拓扑聚合矩阵中该分区所在行移除该分区之后的剩余部分。然后根据式(1)计算输电断面内线路间的潮流分布因子，若某条联络线满足式(2)，则判定该断面为关键输电断面。

关键输电断面的搜索方法具体如下:

(2) 当电网分区对应子矩阵内的联络线数目n≤N时，保留该断面为初始输电断面。其中N为输电断面内的线路数目上限值，其取值由实际运行状况决定。

(3) 根据含潮流方向的电网拓扑聚合矩阵，对步骤(1)、(2)得到的电网分区及对应的联络线进行潮流一致性验证，子矩阵内联络线潮流方向一致的作为初始输电断面。本文规定拓扑聚合矩阵中潮流方向从行节点流向列节点时，矩阵中a值为1，反之a值为-1。

(4) 对保留的电网分区进行连通性判别，剔除不连通的电网分区，保证得到的电网分区具有连通性。

(5) 对符合条件的输电断面内的线路按照式(1)计算潮流分布因子，若断面内的某条线路满足式(2)，则判断该断面为关键输电断面。

(6) 关键输电断面的合并。判定具有相同潮流分布因子的关键输电断面为同一输电断面，只需监视其中一个关键输电断面即可。

(7) 输出电网分区以及对应的关键输电断面。

2 基于磷虾群优化算法的输电断面极限传输功率计算

利用拓扑聚合算法对电网关键输电断面进行搜索后，基于OPF构建关键输电断面极限传输功率的数学模型，采用磷虾群算法进行优化计算，快速准确地计算出断面极限传输功率。

2.1 极限传输功率的定义和数学模型

2.1.1 极限传输功率的定义

极限传输功率是指在当前电网运行状态下，没有过负荷、节点电压越限，满足安全约束的前提下，在线计算某种负荷增长方式下的两个区域间断面线路最大传输能力，其实质是一个电气分区到另一个电气分区可靠输送的最大电能。

2.1.2 基于OPF的极限传输功率数学模型

极限传输功率的数学模型是一个非线性、连续的优化问题，本文基于OPF构造静态安全运行状态下的输电断面极限传输功率的数学模型。在求解某一断面的极限传输功率时，以断面上传输的有功功率最大为优化目标，其目标函数为

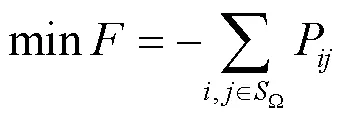
静态安全等式约束为潮流方程约束，如式(5)。不等式约束如式(6)所示，分别为可调发电机组有功、无功出力约束，节点电压幅值约束，线路静态运行约束。

等式约束为

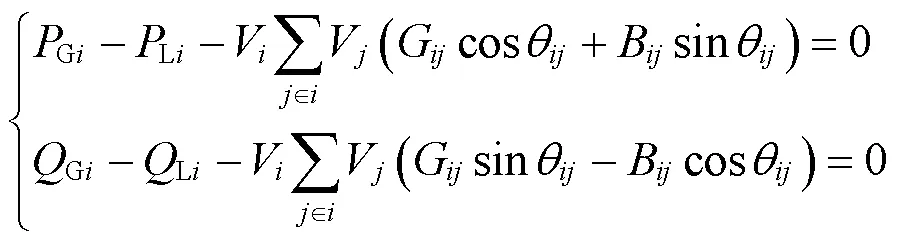
式中：Gi、Gi分别表示节点的有功发电功率和无功发电功率；Li、Li分别表示节点的负荷有功功率和无功功率；V为节点的电压幅值；G、B和θ分别为节点、之间的电导、电纳和相角差。

不等式约束为

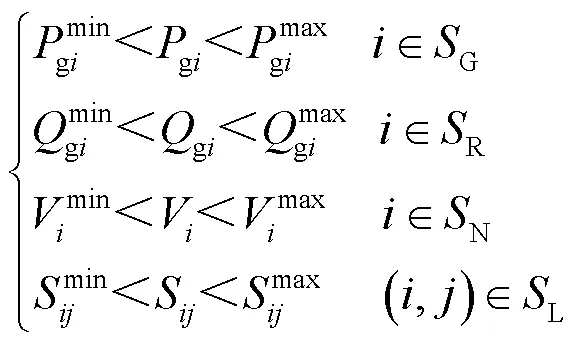
式中：G表示可调有功发电机组集合；R表示可调无功发电机组集合；N表示节点集合；L表示线路集合。

本文采用的负荷增长方式为区域比例负荷增长方式[14]。忽略网损变化的前提下，送电区发电机组有功出力的变化量等于受电区负荷节点有功的变化量，即

2.2 磷虾群优化算法

磷虾群优化算法是一种基于启发式群体智能的求解优化问题的新型优化方法[23]。每个个体不仅受自身历史最优个体和全局最优个体的影响，还受到邻近最优个体和理想最优位置的影响，这些个体同时对当前个体产生进化效果，促使当前个体朝着适应度值更优的方向进化。而且所有个体共享进化信息，具有更快的收敛速度和计算精度。同时磷虾群算法引入交叉、变异概率思想，更容易避免陷入局部最优，具有良好的全局收敛能力。该算法通过执行感应、觅食、扩散3个动作，向适应度值更优的搜索方向更新进化，寻优性能好，操作简单。

2.2.1 个体控制变量的移动位置更新

本文确定控制变量为送电区除平衡机组外的发电机组有功出力g以及对应的发电机节点电压幅值g。个体机组信息位置用控制变量来表示，即

个体在迭代过程按照式(5)进行潮流计算。针对相关变量不满足不等式约束式(6)的个体，采用罚函数法进行处理[24]。

个体机组信息位置用维决策空间的拉格朗日模型建模，如式(10)所示。

式中：N()、F()、D()分别表示由其他个体引起的感应运动、由当前理想最优机组解(食物位置)吸引引起的觅食运动、个体自身的随机扩散运动3种运动向量；为种群当前迭代次数。

在觅食运动中，种群搜索的当前理想最优机组解是一个“理想最优点”，定义为

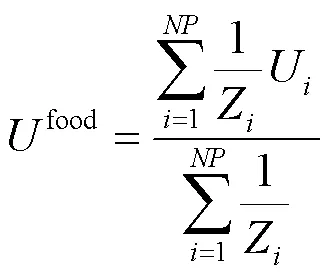
在更新过程中，个体机组信息位置受感应运动、觅食运动和随机扩散运动的协同影响，具体确定方法如式(12)所示。

个体机组信息位置根据式(12)进行更新进化，个体位置更新公式为

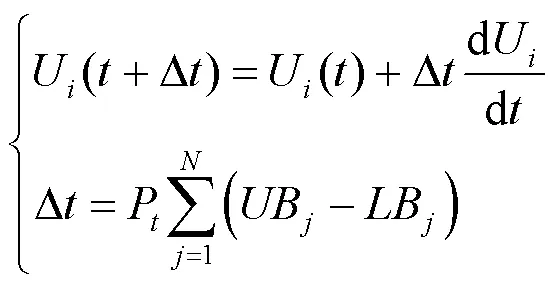
式中：P为步长缩放因子；UB、LB分别为控制变量的上界和下界；为控制变量的维数。

2.2.2 变异、交叉策略

为避免陷入局部最优，增强全局寻优能力，KHA实施遗传算子交叉、变异操作，增加个体机组信息位置的多样性。

交叉操作是指通过替换重组多个父代个体控制变量中的元素，生成新的子代个体的操作。交叉操作公式为

变异操作是指对父代个体控制变量中的元素进行调整。变异操作公式为

为保证算法在前期具有较强的全局搜索能力，尽可能找到全局最优机组解，在后期具有较强的局部搜索能力，提高收敛速度和精度，将权重因子设置为

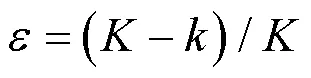
式中：表示当前迭代次数；表示最大迭代次数。随着迭代次数的增加，权重因子由1逐渐变为0，从而降低了U1的权重，逐渐增加了gbest的权重，保证算法具有较强全局搜索能力的同时，具备较快的收敛速度和精度。

3 算法总体流程

基于拓扑聚合算法搜索关键输电断面以及通过磷虾群算法计算断面极限传输功率的流程如图5所示，其具体步骤如下所述。

首先基于拓扑聚合算法对电网关键输电断面进行搜索：

(1) 在线获取电网运行状态和拓扑结构。

图5 输电断面自动搜索和极限传输功率计算流程

(2) 生成电网的邻接矩阵。

(3) 通过拓扑聚合算法将邻接矩阵变换为拓扑聚合矩阵，使拓扑相近的节点聚合在矩阵的主对角线附近。

(4) 按照矩阵的节点排列顺序依次搜索电网分区Area和对应的子矩阵。

(5) 依次对搜索到的电网分区和对应子矩阵进行关键输电断面判别。验证子矩阵包含的联络线数目是否满足n≤N、联络线潮流方向是否一致、线路间潮流分布因子是否满足式(2)以及判断该电网分区是否具有连通性等条件，若同时满足以上关键输电断面判别要求，则该分区对应子矩阵内的联络线为该电网分区的关键输电断面。

(6) 判断所有分区是否都验证完毕。验证完毕则合并相同的关键输电断面，否则转向第(5)步。

(7) 输出电网分区和关键输电断面信息。

得到电网分区和关键输电断面后，基于磷虾群优化算法进行断面极限传输功率的计算：

(1) 对通过关键输电断面辨识流程得到的电网分区以及对应的关键输电断面进行如下操作：根据断面输电线路的潮流方向，将相应的电网分区定义为送电区和受电区，将送电区除平衡机组外的可调发电机组有功出力g和对应的节点电压幅值g作为磷虾群算法的控制变量，断面内的输电线路有功潮流之和作为适应度函数，对磷虾群算法的相关参数进行设置。

(2) 对每个个体，根据控制变量中发电机组有功出力的变化，通过式(7)、式(8)对受电区负荷节点进行相应的有功、无功变化，然后按照等式(5)进行潮流计算。

(3) 针对潮流计算后相关变量不满足不等式约束式(6)的个体，采用罚函数法进行处理。根据适应度函数求取个体机组信息位置的适应度值，确定当前迭代次数下最优个体机组解，通过式(11)产生理想最优机组解。

(4) 更新进化个体机组信息位置，实施遗传算子交叉、变异操作，增加个体机组信息位置的多样性。

(5) 判断当前迭代次数是否达到最大迭代次数，若不满足，重复上述步骤(2)—(4)，直至满足终止条件。若判断满足终止条件，输出该关键输电断面极限传输功率值和最优机组解。

4 算例分析

本文以标准IEEE14节点系统和标准IEEE39节点系统进行算例分析，验证所提方法的有效性。

4.1 基于拓扑聚合算法的关键输电断面辨识

1) IEEE14节点系统的关键输电断面辨识

本文首先对IEEE14节点系统进行关键输电断面的辨识。IEEE14节点系统拓扑结构如图1所示。从图2、图3中可以看出通过拓扑聚合算法，邻接矩阵中节点的排列顺序发生变化，原本分散的节点聚合到矩阵的主对角线附近，使得拓扑紧密的节点聚合在一起，为在矩阵上实现电网的分区和关键输电断面的搜索提供了可能。

表1 IEEE14节点系统关键输电断面搜索结果

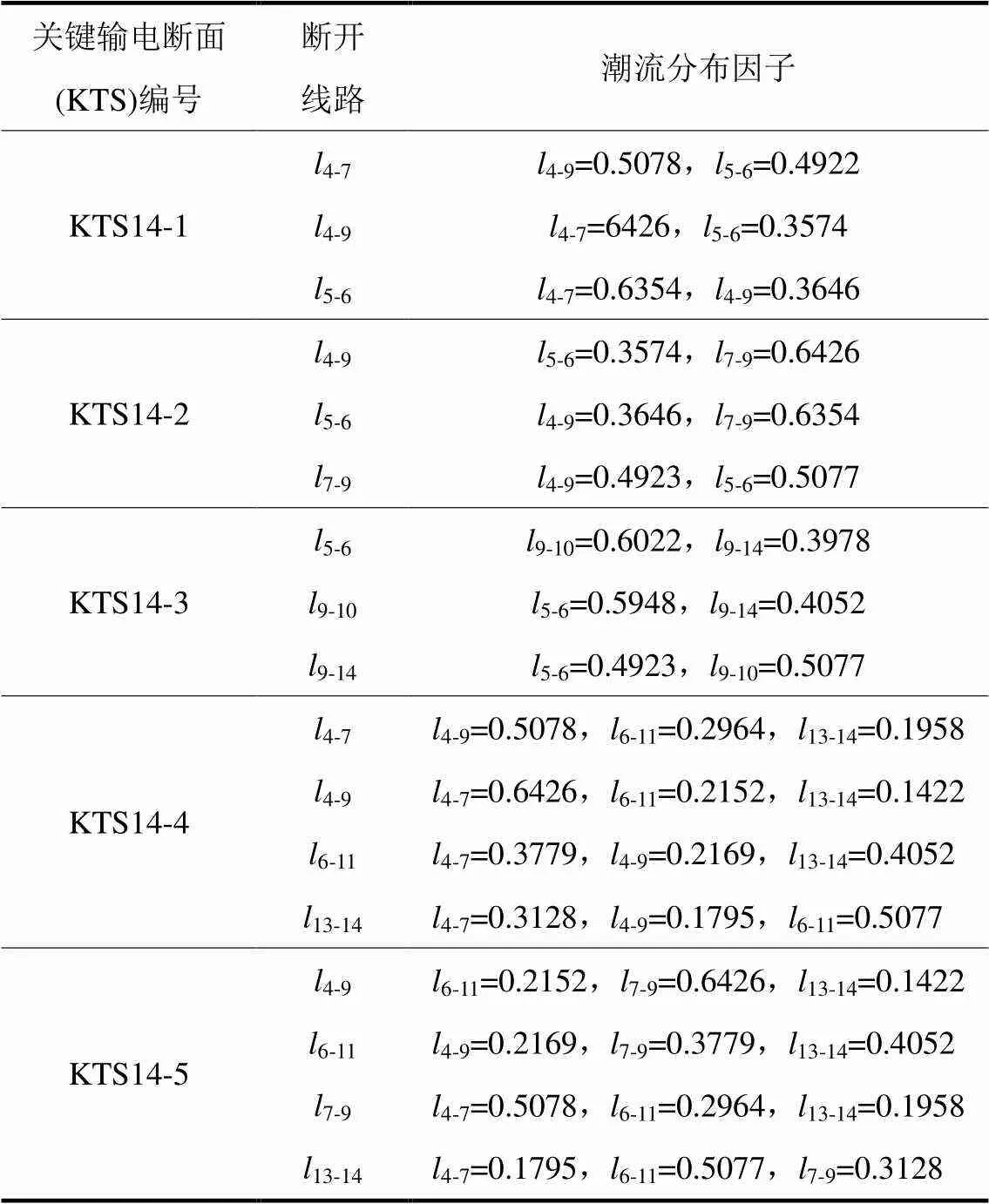
表2 IEEE14节点系统关键输电断面线路间的潮流分布因子

2) IEEE39节点系统的关键输电断面辨识

为进一步验证基于拓扑聚合的输电断面搜索算法的准确性和快速性，对拓扑结构更为复杂的IEEE39节点系统进行输电断面辨识分析。IEEE39节点系统拓扑结构如图6所示。

按照节点编号顺序得到IEEE39节点系统的邻接矩阵，如图7所示，可以看出矩阵中的节点排列顺序无法反映节点间的拓扑距离，从而无法直接在矩阵上进行电网的分区。为实现在矩阵上进行电网分区，对图7所示的邻接矩阵运用拓扑聚合算法进行简单的矩阵行列变换，将分散的节点聚合到主对角线附近，得到如图8所示的拓扑聚合矩阵。

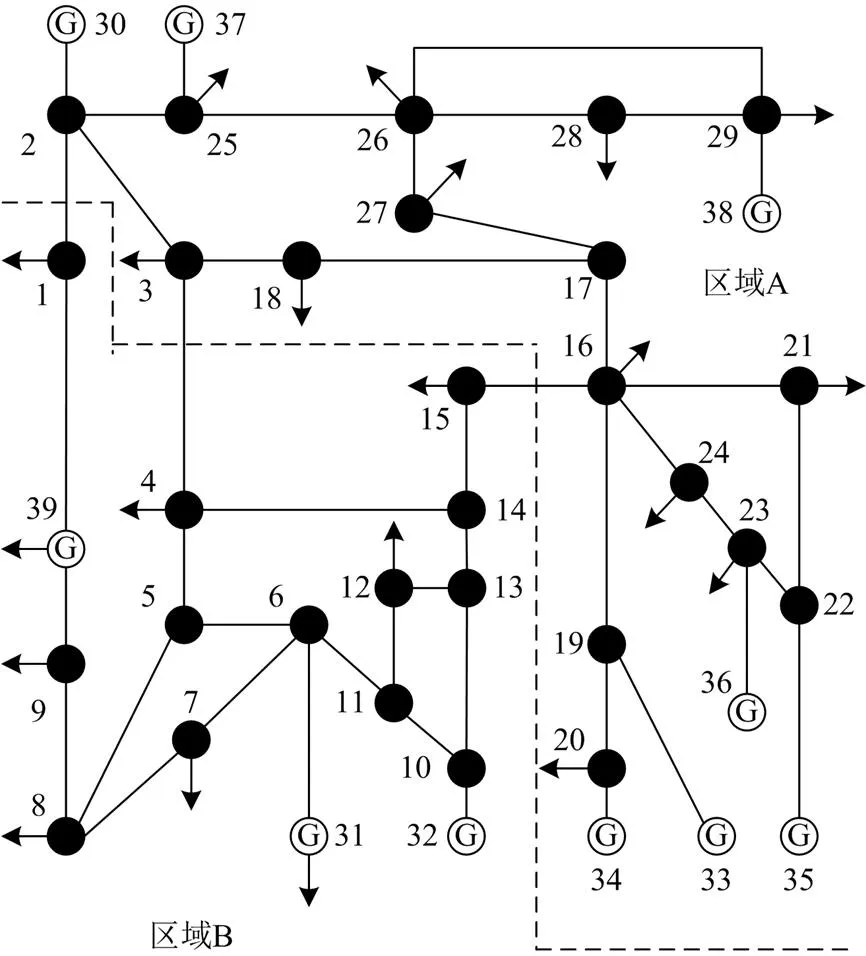
图6 IEEE39节点拓扑结构图

Fig. 6 Topology diagram of IEEE39-bus system

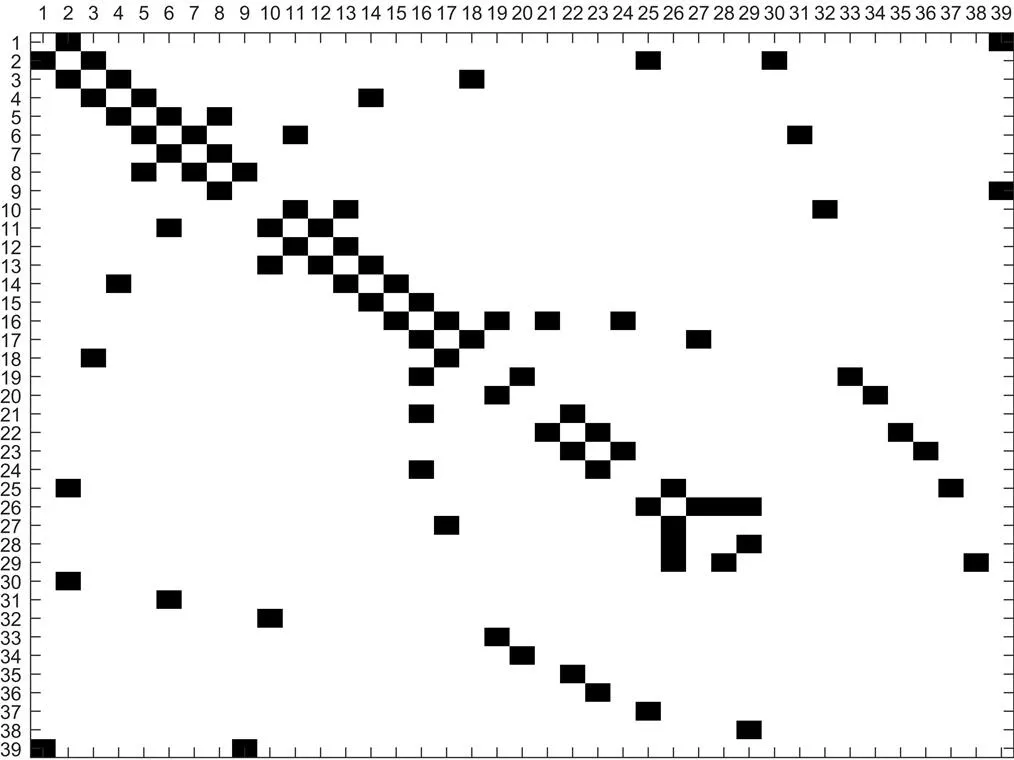
图7 IEEE39节点系统邻接矩阵

图8 IEEE39节点系统拓扑聚合矩阵

Fig. 8 Topology aggregation matrix for IEEE39-bus system

在拓扑聚合矩阵的基础上，通过关键输电断面搜索方法对IEEE39节点系统进行关键输电断面搜索。采用与搜索IEEE14节点系统关键输电断面相同的搜索参数进行IEEE39节点系统的关键断面辨识，判定搜索到的IEEE39节点系统的关键输电断面个数为10个，如表3所示。

表3 IEEE39节点系统关键输电断面搜索结果

如果采用预先分区后遍历割集的方法搜索输电断面，形成的电网分区和搜索到的关键输电断面如图9所示。从结果来看，相较于本文搜索方法，采用预先分区后遍历割集的方法会漏选关键输电断面KTS39-1、KTS39-2、KTS39-4、KTS39-10。分析原因可知：预先分区会导致断面线路13-14处于分区P5中，分区内部的拓扑特性被消除，导致无法搜索到线路13-14，从而造成KTS39-4的遗漏，其他漏选的关键输电断面同理。从搜索耗时上来看，预先分区后遍历搜索方法耗时80 s，而本文的搜索方法耗时只需1.2 s，大大提高了搜索速度。此外对比文献[17,21]搜索到的IEEE39节点系统的关键输电断面，通过拓扑聚合方法搜索到的关键输电断面更为准确，避免了关键输电断面的遗漏。

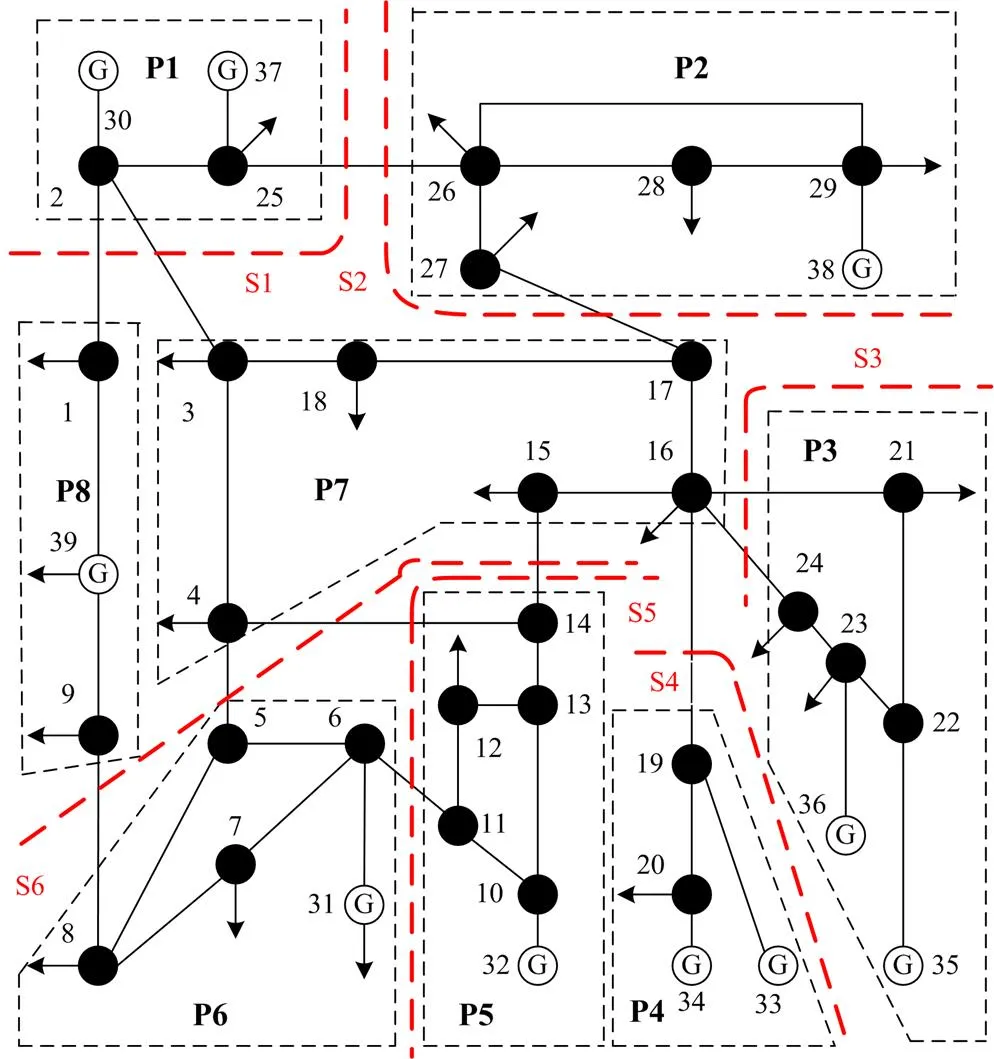
图9 遍历算法搜索关键输电断面的结果

Fig. 9 Search results of key transmission sections by traversal algorithm

4.2 基于磷虾群算法的关键断面极限传输功率计算

通过基于拓扑聚合的输电断面搜索算法搜索出IEEE39节点系统的关键输电断面后，利用KHA进行关键输电断面极限传输功率计算。下面给出表3中KTS39-10的极限传输功率计算说明。

KTS39-10的电网分区如图6所示，KTS39-10包含1-2、3-4、15-163条线路。根据KTS39-10内的联络线潮流方向可知，虚线以上区域A为送电区，虚线以下区域B为受电区。设置送电区内30、33、34、35、36、37、38号发电机的有功出力以及对应的机组电压幅值作为控制变量，受电区节点编号为1、4、7、8、9、12、15、31、39的负荷有功和无功功率按照式(7)、式(8)变化，31号发电机为平衡机组。磷虾群优化算法的参数设置：=100，=200，max=0.01，f=0.02，max=0.005，=0.7，=0.4。通过KHA计算KTS39-10的极限传输功率，其送电区发电机组、平衡机组的最优调整量以及极限传输功率计算值由表4给出。

表4 发电机最优调整量及极限传输功率计算结果

由表4可以看出，通过KHA得到KTS39-10的极限传输功率和最优机组解后，送电区A中大部分发电机组都工作在自身极限边界附近，33、35、36、37、38号发电机组有功出力接近自身极限边界。从理论分析可知，当送电区的所有发电机组有功出力均达到上限时，受电区的负荷节点出力也相应增加，此时得到KTS39-10的极限传输功率是最大的，显然，理论与优化结果不符。分析原因可知：虽然表4中30、34号发电机组有功出力未达到自身极限边界，但此时KTS39-10内断面线路15-16的视在功率为596.44 MVA，接近其视在功率极限边界600 MVA，其他线路2-3视在功率为495.78 MVA，接近其视在功率极限边界500 MVA，说明送电区所有发电机组有功出力均达到极限边界前，线路15-16、2-3静态运行功率极限的约束使30、34号发电机组有功出力未达到极限边界。由此说明，磷虾群优化算法计算输电断面的极限传输功率是符合实际电网运行边界要求的。

磷虾群优化算法求解KTS39-10的极限传输功率收敛曲线如图10所示。从图10可以看出，该算法可以快速收敛到最优机组解，寻优性能好。

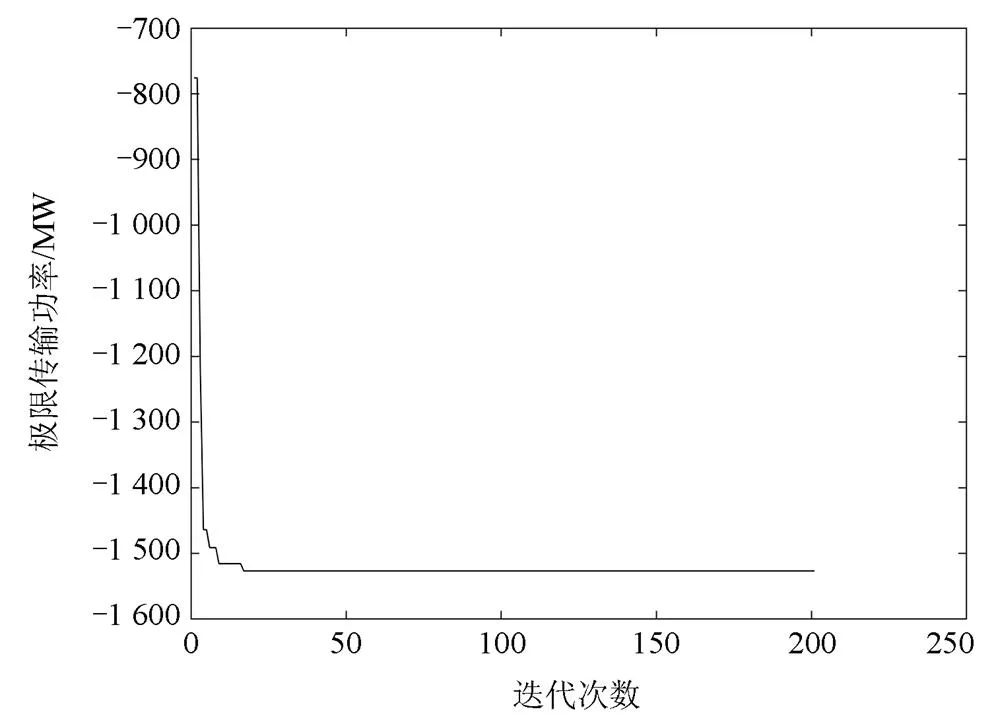
图10 磷虾群优化算法收敛曲线

Fig. 10 Convergence curve of krill herd optimization algorithm

5 结论

随机故障、计划停电等因素使得电网运行方式复杂多变，关键输电断面频繁变动，新能源大规模接入电网以及用户负荷的逐年增加会造成送电区和受电区之间传输的功率波动频繁，因此在线快速识别关键输电断面以及准确计算断面极限传输功率对电力系统在线调度决策具有重要意义。本文提出基于拓扑聚合的电网输电断面搜索方法，通过对邻接矩阵进行简单的矩阵变换操作，将拓扑相近的节点聚合在矩阵主对角线附近，直接在变换后的拓扑聚合矩阵上实现电网的分区以及关键输电断面的搜索，计算速度显著提高，关键断面搜索更加准确。通过磷虾群优化算法构造电网关键输电断面极限传输功率的优化模型，更加准确快速地计算断面极限传输功率。本文所提方法实现调度人员在线快速准确地搜索关键输电断面和掌握电网运行边界，防止线路过载，对保障电力系统安全稳定运行具有重要意义。

[1] RAMPURKAR V, PENTAYYA P, MANGALVEDEKAR H A, et al. Cascading failure analysis for Indian Power Grid[J]. IEEE Transactions on Smart Grid, 2016, 7(4): 1951-1960.

[2] 张玥, 谢光龙, 张全, 等. 美国得州2·15大停电事故分析及对中国电力发展的启示[J]. 中国电力, 2021, 54(4): 192-198, 206.

ZHANG Yue, XIE Guanglong, ZHANG Quan, et al. Analysis of 2·15 power outage in texas and its implications for the power sector of China[J]. Electric Power, 2021, 54(4): 192-198, 206.

[3] 严道波, 文劲宇, 杜治, 等. 2021年得州大停电事故分析及其对电网规划管理的启示[J]. 电力系统保护与控制, 2021, 49(9): 121-128.

YAN Daobo, WEN Jinyu, DU Zhi, et al. Analysis of Texas blackout in 2021 and its enlightenment to power system planning management[J]. Power System Protection and Control, 2021, 49(9): 121-128.

[4] 任建文, 李刚, 王增平, 等. 基于背离路径的输电断面搜索新算法[J]. 电网技术, 2012, 36(4): 121-127.

REN Jianwen, LI Gang, WANG Zengping, et al. New algorithm for searching tie lines based on deviation paths[J]. Power System Technology, 2012, 36(4): 121-127.

[5] 王增平, 李刚, 任建文. 基于前K最短路径的输电断面搜索新算法[J]. 电工技术学报, 2012, 27(4): 193-201.

WANG Zengping, LI Gang, REN Jianwen. A new search algorithm for transmission section based on K shortest path[J].Transactions of China Electrotechnical Society, 2012,27(4): 193-201.

[6] 周德才, 张保会, 姚峰, 等. 基于图论的输电断面快速搜索[J]. 中国电机工程学报, 2006, 26(12): 32-38.

ZHOU Decai, ZHANG Baohui, YAO Feng, et al. Fast search for transmission section based on graph theory[J]. Proceedings of the CSEE, 2006, 26(12): 32-38.

[7] 赵峰, 孙宏斌, 张伯明. 基于电气分区的输电断面及其自动发现[J]. 电力系统自动化, 2011, 35(5): 42-46.

ZHAO Feng, SUN Hongbin, ZHANG Boming. Electrical zone division based automatic discovery of flowgates[J]. Automation of Electric Power Systems, 2011, 35(5): 42-46.

[8] 王涛, 李渝, 顾雪平, 等. 考虑地理分区边界优化的电网关键输电断面辨识[J]. 电工技术学报, 2014, 29(4): 220-228, 245.

WANG Tao, LI Yu, GU Xueping, et al. Identification of the key transmission sections considering optimization of geographical partition boundary for power grids[J]. Transactions of China Electrotechnical Society, 2014, 29(4): 220-228, 245.

[9] 孙淑琴, 颜文丽, 吴晨悦, 等. 基于原-对偶内点法的输电断面有功安全校正控制方法[J]. 电力系统保护与控制, 2021, 49(7): 75-85.

SUN Shuqin, YAN Wenli, WU Chenyue, et al. Active power flow safety correction control method of transmission sections based on a primal-dual interior point method[J]. Power System Protection and Control, 2021, 49(7): 75-85.

[10] ZHANG D, WANG N, YANG H, et al. Fast search algorithm for key transmission sections based on topology converging adjacency matrix[J]. IEEE Access, 2020, 8: 108235-108246.

[11] 王乃静. 基于邻接矩阵拓扑聚合的输电断面快速搜索及考虑机组调整时延的潮流控制策略[D]. 合肥: 合肥工业大学, 2020.

WANG Naijing. Fast search algorithm for transmission sections based on topology converging of adjacency matrix and power flow control strategy considering units adjustment delay[D]. Hefei: Hefei University of Technology, 2020.

[12] 赵晋泉, 张伯明. 连续潮流及其在电力系统静态稳定分析中的应用[J]. 电力系统自动化, 2005, 29(11): 91-97.

ZHAO Jinquan, ZHANG Boming. Summarization of continuation power flow and its applications in static stability analysis of power system[J]. Automation of Electric Power Systems, 2005, 29(11): 91-97.

[13] 卢俊, 刘天琪, 南璐, 等. 基于改进连续潮流的输电断面热稳定功率极限计算[J]. 科学技术与工程, 2019, 19(20): 221-228.

LU Jun, LIU Tianqi, NAN Lu, et al. Approach of thermal stability power limit for transmission sections calculation based on improved continuous power flow method[J]. Science Technology and Engineering, 2019, 19(20): 221-228.

[14] 姜臻, 苗世洪, 尚亚男, 等. 基于电压崩溃指数的极限传输容量实用计算方法[J]. 电工技术学报, 2014, 29(10): 213-221.

JIANG Zhen, MIAO Shihong, SHANG Yanan, et al. Voltage collapse indices based method for practical computation of total transfer capability[J]. Transactions of China Electrotechnical Society, 2014, 29(10): 213-221.

[15] 汪峰, 白晓民. 基于最优潮流方法的传输容量计算研究[J]. 中国电机工程学报, 2002, 22(11): 35-40.

WANG Feng, BAI Xiaomin. OPF based transfer capability calculation[J]. Proceedings of the CSEE, 2002, 22(11): 35-40.

[16] 徐正清, 肖艳炜, 李群山, 等. 基于灵敏度及粒子群算法的输电断面功率越限控制方法对比研究[J]. 电力系统保护与控制, 2020, 48(15): 178-184.

XU Zhengqing, XIAO Yanwei, LI Qunshan, et al. Comparative study based on sensitivity and particle swarm optimization algorithm for power flow over-limit control method of transmission section[J]. Power System Protection and Control, 2020, 48(15): 178-184.

[17] 马菁曼, 邱晓燕, 陈科彬. 基于鸡群算法的断面传输极限的自动搜索断面研究[J]. 电测与仪表, 2018, 55(3): 31-36.

MA Jingman, QIU Xiaoyan, CHEN Kebin. Research on the automatic searching section of the section transmission limit based on the chicken swarm optimization algorithm[J]. Electrical Measurement & Instrumentation, 2018, 55(3): 31-36.

[18] 王俊, 蔡兴国. 差分进化算法在考虑暂态稳定约束的最大输电能力计算中的应用[J]. 电网技术, 2010, 34(3): 96-100.

WANG Jun, CAI Xingguo. Application of differential evolution algorithm in total transfer capacity calculation with transient stability constraints being considered[J]. Power System Technology, 2010, 34(3): 96-100.

[19] SINGH G P, SINGH A. Comparative study of krill herd, firefly and cuckoo search algorithms for unimodal and multimodal optimization[J]. Intelligent Systems and Application, 2014, 3: 35-49.

[20] WANG Gaige, GUO Lihong, WANG Heqi, et al. Incorporating mutation scheme into krill herd algorithm for global numerical optimization[J]. Neural Computing and Applications, 2014, 24(3-4): 853-871.

[21] 王红壮, 刘天琪, 何川, 等. 基于改进脆弱线路辨识的关键输电断面确定方法[J]. 现代电力, 2020, 37(3): 295-301.

WANG Hongzhuang, LIU Tianqi, HE Chuan, et al. Key transmission section determination method based on improved vulnerable line identification[J]. Modern Electric Power, 2020, 37(3): 295-301.

[22] 徐俊明. 图论及其应用[M]. 合肥: 中国科学技术大学出版社, 2004.

[23] MUKHERJEE A , ROY P K , MUKHERJEE V. Transient stability constrained optimal power flow using oppositional krill herd algorithm[J]. International Journal of Electrical Power & Energy Systems, 2016, 83: 283-297.

[24] DE TUGLIE E, DICORATO M. A static optimization approach to assess dynamic available transfer capability[J]. IEEE Transactions on Power Systems, 2000, 15(3): 1069-1076.

A method of identifying a transmission section based on topology aggregation and the transmission limit of the section

ZHANG Dabo, WANG Boxin, GUO Huaixin, CHU Zhuwei, YANG Hejun, MA Yinghao

(Anhui Province Key Laboratory of Renewable Energy Utilization and Energy Saving (Hefei University of Technology), Hefei 230009, China)

Many blackouts at home and abroad show that the transmission section is the weak link in a large-scale interconnected power grid. It is helpful for the dispatching department to adjust operational mode in time to avoid large area blackout incidents by quickly searching the key transmission section and calculating the limit transmission power of the section. In this paper, a topological aggregation algorithm is proposed to search the key transmission sections of the power network. Adjacent nodes in the topology are aggregated to the main diagonal of the adjacency matrix by simple matrix transformation. The power flow distribution factor is used to identify the key transmission section by searching the network transmission section directly on the transformed adjacency matrix. The optimal model of the limit transmission power of the key transmission section is constructed using the krill herd optimization algorithm to accurately calculate the limit transmission power of the section. Work on the IEEE14 node system and IEEE39 node test system verify the effectiveness of the proposed method.

key transmission section; adjacency matrix; topology aggregation; krill herd optimization algorithm; limit transmission power

10.19783/j.cnki.pspc.210832

国家自然科学基金重点项目资助(51637004)

This work is supported by the Key Project of National Natural Science Foundation of China (No. 51637004).

2021-07-05；

2021-09-23

张大波(1979—)，男，硕士生导师，研究方向为电网可靠性评估和规划调度；E-mail: zhangdb2004@163.com

王博欣(1996—)，男，硕士研究生，研究方向为电网智能调度。E-mail: wbx17854299083@163.com

(编辑 魏小丽)