浮动平均值在大变形隧道定额测定与分析中的应用

李 准 张 穷

(中铁二院工程集团有限责任公司， 成都 610031)

我国西南地区长期处于地壳活动强烈地带，地形切割陡峻，地质构造复杂，素有中国“地质博物馆”之称，在此区域施工存在巨大的特殊地质灾害风险[1]。因铁路隧道定额的普遍性和通用性，未能全面考虑各类特殊复杂地质灾害引起的安全、资源投入变化情况，西南地区铁路隧道施工一旦遇到大变形地质灾害，现行定额无法充分反映其安全、质量、进度成本投入，致使项目投资不足，增加了建设单位、设计单位和施工单位设计变更的工作量和投资控制难度[2]。针对这一情况，本文开展了以新建丽江至香格里拉铁路软岩大变形为基础的定额测定工作，在软岩三台阶带仰拱一次开挖工法条件下通过不同大变形段施工断面(大变形Ⅰ、Ⅱ、ⅡA、ⅢA)参数分析，对不同变形条件下的资源消耗、成本投入情况进行研究，通过对常规定额水平以外的特殊复杂地质条件下隧道施工资源消耗、成本投入情况等进行研究分析，有针对性的提出概预算编制调整意见或编制专项补充施工定额，为丽香铁路投资控制及以后大丽攀、滇藏铁路等类似重大工程设计概预算编制提供参考。

1 项目背景

新建丽江至香格里拉铁路位于云南省西北部，南起大丽铁路丽江车站，向北跨越金沙江，经小中甸至香格里拉，全长139.652 km。线路连接大理至丽江铁路，并通过该铁路和广大铁路与成昆铁路相联，是我国中长期铁路网规划中西部路网的重要组成部分。

新建丽香铁路地处欧亚板块和印度洋板块相互碰撞汇聚形成的青藏高原东南缘之川滇菱形断块的西部边界断裂带(金沙江—中甸断裂带)内，属我国著名的南北向地震带南段之滇西地震带，地质构造复杂，新构造运动强烈[3]。受大规模地质构造的强烈挤压影响，隧道通过之处应力集中度高、多期岩浆侵入的地质环境下存在极高地应力。

2 浮动平均值

浮动平均值求解法是数理统计学在实际应用中的一种拓展[4]。该方法主要用于改善当数据样本存在一定变动或实测数据波动较大，存在较大误差时，采用传统平均值求解法的适用性和准确性。

传统的数理统计方法是以总体分布为正态分布作为前提推导得出的[5]。从基本概念的推导过程中不难看出，在样本总体呈正态分布的情况下，这些统计方法具有良好的稳定性，得到结果具有足够的准确性。但对于大多数工程应用的实际案例，正态分布的假设通常只能近似地满足，有时甚至无法满足。基于这一类波动性较强的数据样本，统计方法稳健性的研究和应用具有很大的实际意义[6]。

由于在实际观测中提取的数据量通常较大，很难完全甄别出所有的异常数据。而如果异常数据中有极大或极小值的存在，传统的算术平均数的稳定性就会降低。为增加平均数的准确性，通常有两种途径：一是采用有效的方法或将数据尽可能地缩小至更加有效的范围，以筛选出数据中的异常值把它们直接剔除，然后进行传统平均值的计算；二是设计新的统计方法使得样本数据中的异常值不会对最终结果有过大的影响，一般基于绝对偏差和最小原则，或给中位数赋予更高的权重，使得样本的集中趋势和统计结果的稳定性有所改善。

第一种方法作为数理统计学中的一个重要课题，长久以来一直受到科研工作者们的广泛关注，针对拥有庞大数据量的样本效果显著。但是若样本的数据量偏小，则无法利用其自身规律和趋势找出异常值或缩小样本数据的有效范围，第一种方法就难以发挥作用。而且，即使可以正确地确定某些异常数据，在剔除异常数据后，如果剩余的样本数量太小，同样可能会导致最终结果的准确性降低。因此，考虑到此课题中实际工程应用背景，本文选用第二种思路对算术平均值进行改进。浮动平均法中考虑样本中异常数据对传统平均值的影响，引入参数θ，使得所求得的浮动平均值可根据实际情况(即异常数据在整个样本中的分布和多寡情况)，选择更加接近中位数或是算术平均值，能够比较灵活地在两者之间浮动切换。

假设数据样本为：x1,x2, …,xn。

样本数据的标准差可通过式(1)求得：

(1)

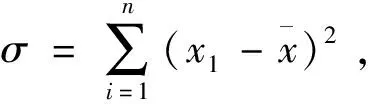
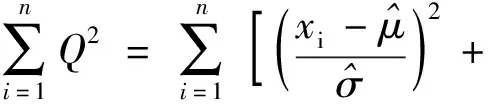
(2)

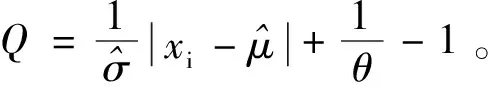
浮动平均法不仅依据样本中的数据对距离算术平均值的远近相应地赋予了权重，更进一步引入了参数θ，可根据数据处理的实际背景情况和需要，调整那些距离算数平均值较远数据的权重。例如，在某些情况下，一些实测的数据虽然距离样本算术平均值的距离较远，但仍正确地反应了样本的某种特性，需赋予与距离较近的数据相当的权重以正确地反馈出样本的这种特性。但当我们使用稳健平均值进行数据分析的时候，这些客观上距离样本算术平均值较远的数据会被自然地分配上较低的权重，对最终得到的平均值产生误导。因此，浮动平均法在工程实测数据分析的客观性和正确性上均优于稳健平均法。

3 成果运用

3.1 研究样本

课题以新建丽香铁路中义、七达里、宗思隧道(设计有效断面30.97 m2，净空宽4.54 m，高6.75 m)为样本进行数据采集，对工作条件、步骤相近相似的工序进行合并和细化，重点突出拟编制子目高地应力强烈挤压变质区大变形的特点[7]。通过确定开挖、出渣、钢拱架制安、喷射混凝土(机械手)、超前小导管施作、注浆、树脂锚杆施作、混凝土拌制浇筑运输、监控量测、通风管线路、大变形段拆换钢拱架及钢筋网、大变形圬工非爆凿除及机械拆除等20余个工序的施工组织模型，并以浮动平均法和算数平均法对测定的数千个数据进行分别处理和对比，以验证浮动平均法的正确性及优越性。受篇幅所限，本文仅以其中中义隧道出口工区和2号横洞工区基础数据为例。

3.2 基于R语言的数据处理

由于浮动平均值需通过求解式(2)得到，为得到最优Q值，需进行大数据测算，为提高工作效率，本文采用R语言编程进行求解。R语言是一款用于统计分析的语言和操作环境。与之相配套的RGui软件集统计分析与图形展示为一体，可自由编写程序代码，且完全开源，是统计领域一种非常实用的计算工具[8]。

最终，得到具体计算结果如表1、表2所示，其中参数θ=0.5。

表1 出口正东基础延续时间的两种平均值对比表

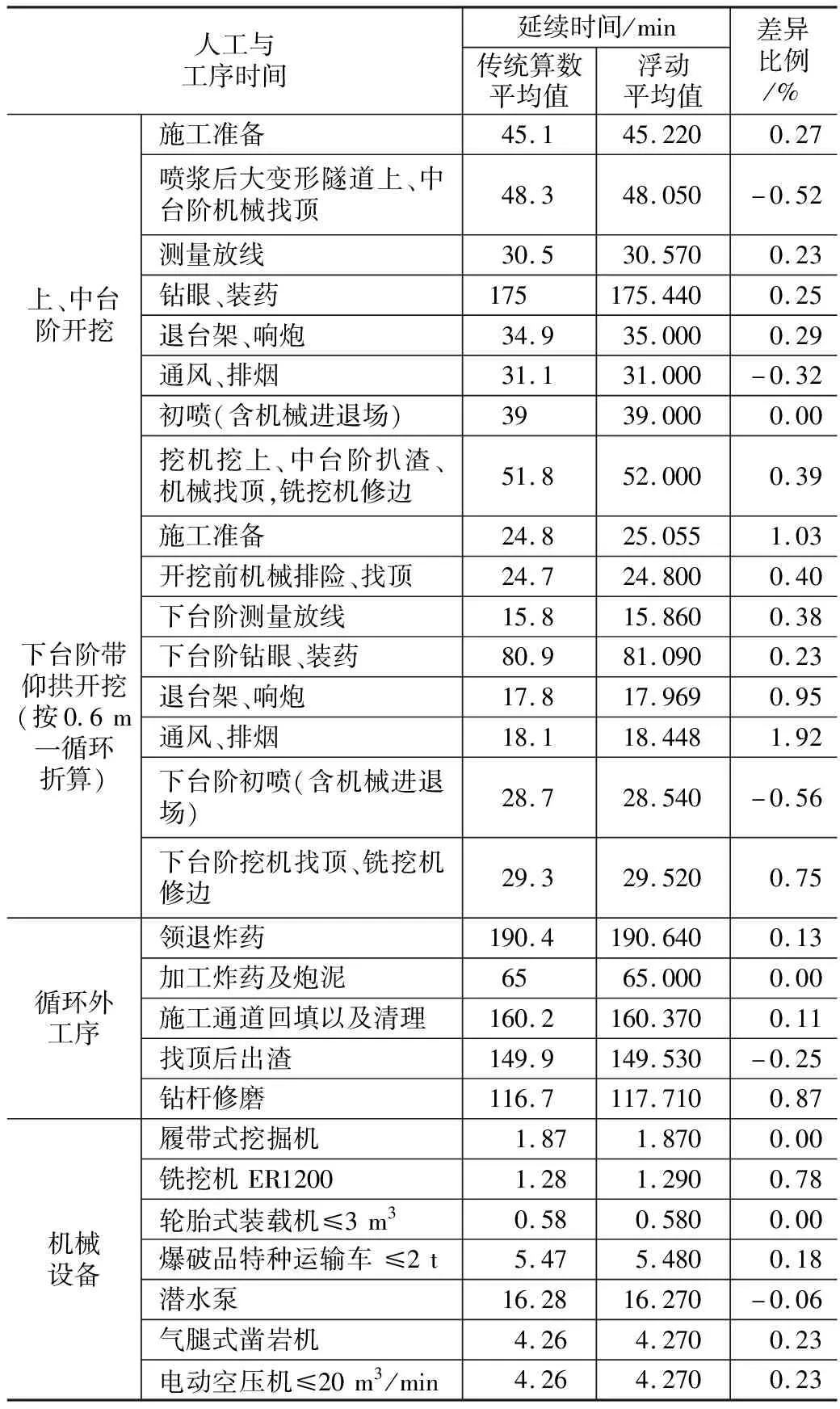
表2 2号横道正洞基础延续时间的两种平均值对比表

3.3 分析结果

从上表中的各项结果可以看出，求得的浮动平均值与传统算术平均值大致相等。在对平均值和中位数给予相等权重的前提条件下(θ=0.5)，浮动平均值与算术平均值之间的差值基本控制在2.5%以内。首先，从结果中不难看出，所有数据的浮动平均值均与传统算数平均值接近，体现出了浮动平均值的有效性；其次，由于浮动平均法将中位数考虑了进去，远离中位数的数据对最终结果的影响降低，远离样本中心的异常数据对最终结果的影响被人为减小，从而使得所得到的结果比传统算术平均值更加真实。

对于不同的实际工程背景，由于统计方式和工作条件不同，出现异常值的潜在可能情况各有不同。某些场景中，有些数据虽距离样本中位数较远，但却真实地反应了该数据项目的某种特性，需给它们赋予与其他距离中位数较近的数据相同的权重，才能使最终求得的平均值能够更好地体现该组样本所对应的数据特性。因此，在这种情况下，参数θ的设置可以更加接近1。对于相反的情形，若想对接近中位数的数据赋予更大的权重，则可以将参数θ设置更加接近0。

4 结束语

传统的算术平均值可有效地处理大部分较为连续且分布比较集中的样本数据。但对于许多工程项目中所涉及到的样本数据，由于其数据收集方式和收集环境存在一些难以克服的自然误差，在处理这些样本的时候，需寻找一种科学的数学途径，有效地减少异常数据对最终平均值的影响。本文提出的浮动平均法在处理实际工程数据时，可根据样本数据中异常数据分布位置距离样本中位数的远近，通过调节参数θ来有效降低异常数据对平均值产生的影响。综上所述，该方法主要适用于已经大致了解异常数据分布位置的工程样本数据，根据所知异常数据分布信息调节参数θ求得的浮动平均值的准确性将优于传统算术平均值。