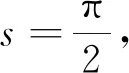2× 2中具有常Jordan角局部共形平坦超曲面

卢小格，王 鹏，王孝振

(福建师范大学数学与统计学院,福建 福州 350117)

(1)M是常平均曲率超曲面，当且仅当以下 3 种情形之一成立.

(i)C2=1，且f(M)是1(r)×2(r∈(0,1])的一个开集;

(ii)C=0，且f(M)是Mt的一个开集，其中

Mt={(p,q)∈2×2|〈p,q〉=t};

(1)

(iii)C=0，且M是一个数量曲率不为常数的非完备极小超曲面.

(2)M是常数量曲率超曲面，当且仅当以下 3 种情形之一成立.

(i)C2=1，且f(M)是1(r)×2(r∈(0,1])的一个开集;

(ii)C=0，且f(M)是Mt的一个开集;

(iii)C=0，且M是一个平均曲率不为常数且截面曲率为1/2的非完备超曲面.

另外，在黎曼流形的研究中，局部共形平坦结构是一个重要的几何研究对象，因此对局部共形平坦黎曼流形进行分类具有重要意义.1999年，成庆明等[9]在数量曲率r和Ricci曲率模长平方S都是正值常数的假设条件下，得到了3维完备局部共形平坦流形的分类定理.

C=〈Pξ,ξ〉=cos2s,

(2)

其中

(3)

这里,

且

m2cots=s1,m3cots=n1tans，n2tans=s3,

(4)

其中θij是M的联络 1-形式.特别地,{m1,m3,n3,s}满足M的可积条件

(5)

其中

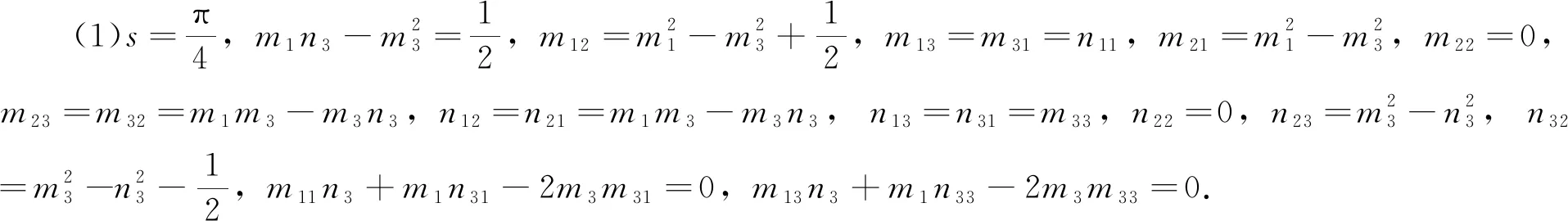
(1)若M是Einstein超曲面，则M是局部共形平坦超曲面.

(2)若M是常数量曲率超曲面，则M是局部共形平坦超曲面当且仅当以下 2 种情形之一成立.

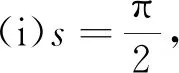
注1由文[8]的例3.3可知，取定点a,b∈2，则2×2|〈p,a〉2+〈q，b〉2=1}是一族平均曲率不为常数且截面曲率为1/2的非完备超曲面.

(6)

其中

令E4=ξ,E5=N，由式 (6) 有

(7)

其中θi为Ei的对偶基底.设

其中mi和ni是M上的光滑函数.则

假设f在2×2和的第二基本形式分别为

则由上述方程得到

(8)

(9)

其中

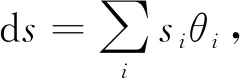
(10)

由式(8)推得M在2×2中平均曲率为

对式(7)进行外微分，得到M的可积条件

(11)

其中

(12)

m22=m1s1tans-m3s3cots+s12tans+s1s2tan2s+s1s2sec2s,

(13)

m23=m1m3-m3n3+s1s3sec2s+s13tans+s2m3tans,

(14)

m31=n11tan2s+m1s3tans+2m3s1secscscs+m3s1cots,

(15)

n13=m33cot2s-m3s3cots-2m3s3cotscsc2s-n3s1cots,

(16)

n21=m1m3cot2s-m3n3cot2s-s1s3csc2s+s31cots-s2m3cot3s,

(17)

n22=m3s1cots-n3s3cots+s32cots-s2s3cot2s-s2s3csc2s,

(18)

(19)

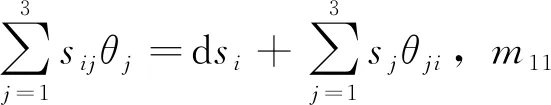
m2cots=s1,m3cots=n1tans，n2tans=s3.

(20)

(21)

其中m11和n33为M上的函数，且m2=0，n1=m3cot2s，n2=0.

(22)

其中

设

类似 1.1 节的计算，得到

2.1 3维局部共形平坦黎曼流形

设(M3,g)是3维黎曼流形，选取局部标准幺正标架场{ei}(i=1,2,3)及其对偶标架场{ωi}.M3的Ricci曲率Rij和数量曲率r分别定义为

(23)

由Bianchi恒等式，有

(24)

其中Rij,k和ri分别为Ricci曲率Rij和数量曲率r的协变导数.

M3的Wely张量Cijk(1≤i,j,k≤3)定义为

(25)

引理2[10]黎曼流形(M3,g)是局部共形平坦流形的充分必要条件是Cijk=0(1≤i,j,k≤3).

(26)

因为M是2×2中具有非退化常Jordan角的定向超曲面，则由式(10)推得

s1=s2=s3=0，m2=0，n1=m3cot2s，n2=0.

将上述方程结合式(8)，式(9)，式(23)和式(26)直接计算得到

(27)

式(23)结合式(27)推出

(28)

进一步得到

R11,1=dR11(E1)=R33,1=dR33(E1)=m11n3+m1n31-2m31m3cot2s,

(29)

R11,2=dR11(E2)=R33,2=dR33(E2)=m12n3+m1n32-2m32m3cot2s,

(30)

R11,3=dR11(E3)=R33,3=dR33(E3)=m13n3+m1n33-2m33m3cot2s,

(31)

R12,1=R21,1=(R11-1)m1，

(32)

R12,3=R21,3=(R11-1)m3,

(33)

R23,1=R32,1=(1-R33)m3cot2s,

(34)

R23,3=R32,3=(1-R33)n3,

(35)

Rij,k=0(i,j,k取其他值).

(36)

进而，式 (24)和式(25)结合式(29)-(36)得到

C123=-C132=R12,3,

C213=-C231=R12,3-R23,1,

C312=-C321=-R23,1,

Cijk=0(i,j,k取其他值).

若M是共形平坦超曲面，即上述方程同时为零，此时得到

R11,2=2R12,1=2R23,3，且R11,1=R11,3=R12,3=R23,1=0.

(37)

将R12,3=R23,1=0代入式(33)和式(34)解得R11=R33=1或者m3=0.由R11=R33=1结合引理1计算得到定理4的情形1，由m3=0结合引理1计算得到定理4的情形 2.反之，显然成立.

由上述的推导过程得到如下命题.

文[8]中Urbano构造了一族齐性超曲面Mt(见式(1))，这里，将利用定理4证明Mt不是局部共形平坦超曲面.

例1 设

Mt={(p,q)∈2×2| 〈p,q〉=t,t∈(-1,1)}.

则Mt≅SO(3)是2×2中C=0(即的超曲面.令A=(η1,η2,η3)∈SO(3),定义ft:SO(3)2×2为

ft(A)=(η1,η1cosφ+η2sinφ)=(p,q).

那么M的规范标架取为

直接计算得到

于是

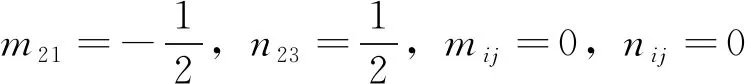
综上，得到如下命题.

命题1Mt不是局部共形平坦超曲面.

另外，利用定理4 还得到如下命题.

R11=R22=1，R12=R13=R23=R33=0.

(38)

进而推得

Cijk=0(1≤i,j,k≤3).

综上，得到如下命题.

若M是具有退化Jordan角的共形平坦超曲面，由式(38)推出M不是Einstein超曲面.所以，只考虑具有非退化常Jordan角Einstein超曲面的情形.此时，由推论1推出M是局部共形平坦超曲面.