有限域上线性化多项式与正规基
2022-03-16徐碧云肖义丽
徐碧云, 肖义丽, 曹 炜
有限域上线性化多项式与正规基
徐碧云1, 肖义丽1, 曹 炜2*
(1.宁波大学 数学与统计学院, 浙江 宁波 315211; 2.闽南师范大学 数学与统计学院, 福建 漳州 363000)

有限域; 正规基; 线性化多项式
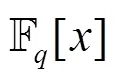

1986年, Pei等[4]证明了定理2.

2001年, Chang等[5]进一步证明了定理1和定理2的充分条件也是必要的, 从而得到了定理3.



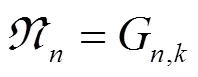
1 线性化多项式
线性化多项式的许多相关性质与结论可参考文献[1,8-11].
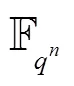

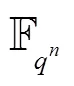



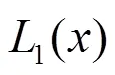

引理2[1]
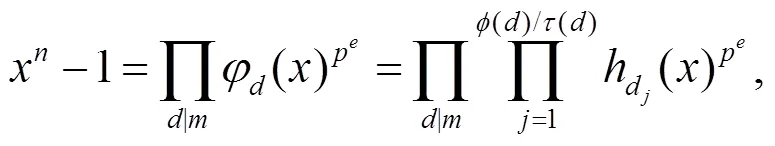
推论2
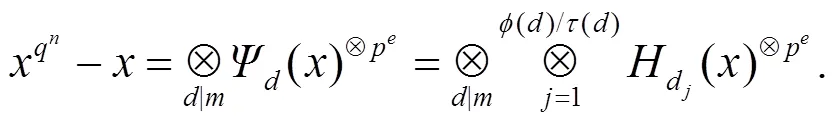
引理3[1]
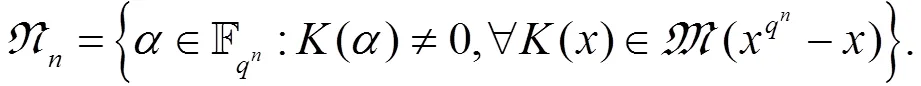
定理5[12]
证明

由容斥原理得:


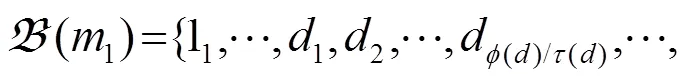
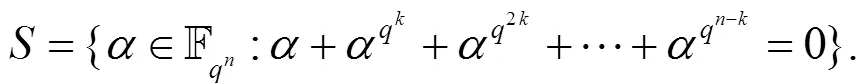

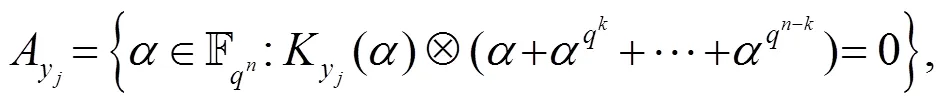
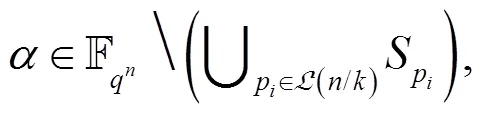

引理4 由定义4, 得到如下集合:
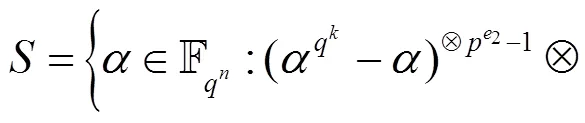




证明 由于

又因为

所以
可得:

由定义4可得式(3), 同理可得式(4)~(6).
引理5 假设
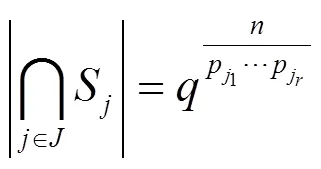

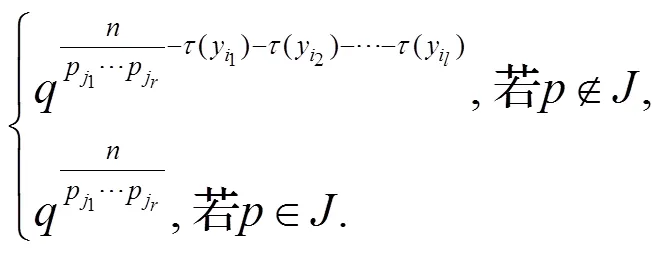
由引理4可以得到:
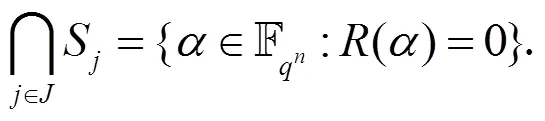
由欧拉函数性质得:


由定义4得:


即式(8)得证.



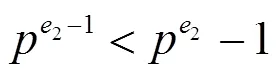
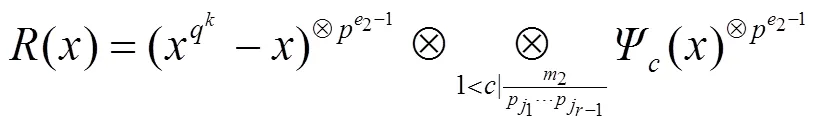
所以

其中:
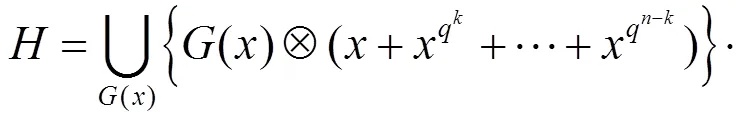
定理6




由容斥原理和引理5可得:
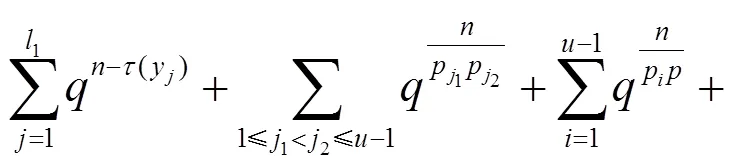
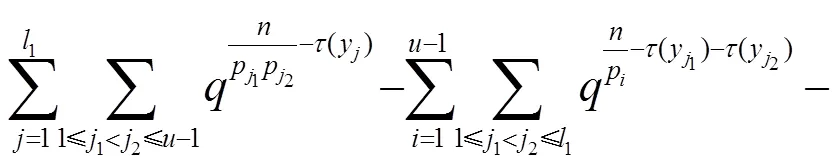
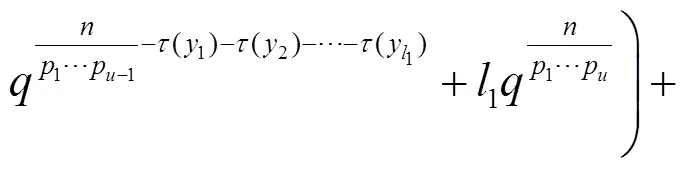
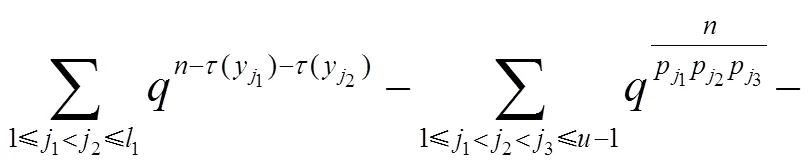
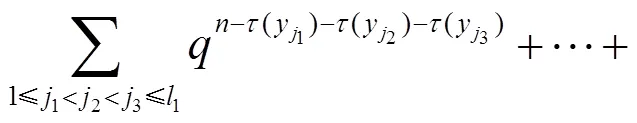

则由式(10), 得到:

[1] Lidl R, Niederreiter H. Finite Fields[M]. Cambridge: Cambridge University Press, 1997.
[2] Mullen G L, Panario D. Handbook of Finite Fields[M]. London: Chapman and Hall, 2013.
[3] Perlis S. Normal bases of cyclic fields of prime-power degree[J]. Duke Mathematical Journal, 1942, 9(3):507- 517.
[4] Pei D, Wang C, Omura J. Normal basis of finite field GF(2)[J]. IEEE Transactions on Information Theory, 1986, 32(2):285-287.
[5] Chang Y, Truong T K, Reed I S. Normal bases over GF(q)[J]. Journal of Algebra, 2001, 241(1):89-101.
[6] Huang H, Han S M, Cao W. Normal bases and irreducible polynomials[J]. Finite Fields and Their Applications, 2018, 50:272-278.
[7] Hachenberger D. Characterizing normal bases via the trace map[J]. Communications in Algebra, 2004, 32(1): 269-277.
[8] Zan H X, Cao W. Powers of polynomials and bounds of value sets[J]. Journal of Number Theory, 2014, 143:286- 292.
[9] Polverino O, Zullo F. On the number of roots of some linearized polynomials[J]. Linear Algebra and Its Applications, 2020, 601:189-218.
[10] Polverino O, Zini G, Zullo F. On certain linearized polynomials with high degree and kernel of small dimension[J]. Journal of Pure and Applied Algebra, 2021, 225(2):106491.
[11] Hu W Y, Zhang Z C, Tu Z H, et al. Efficient computation of the nearest polynomial by linearized alternating direction method[J]. Applied Mathematics and Computation, 2021, 395:125860.
[12] von zur Gathen J, Giesbrecht M. Constructing normal bases in finite fields[J]. Journal of Symbolic Computation, 1990, 10(6):547-570.
Linearized polynomials and normal bases in finite fields
XU Biyun1, XIAO Yili1, CAO Wei2*
( 1.School of Mathematics and Statistics, Ningbo University, Ningbo 315211, China;2.School of Mathematics and Statistics, Minnan Normal University, Zhangzhou 363000, China )
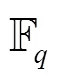
finite field; normal basis; linearized polynomial
O156
A
1001-5132(2022)02-0022-05
2021−04−24.
宁波大学学报(理工版)网址: http://journallg.nbu.edu.cn/
国家自然科学基金(11871291).
徐碧云(1996-), 女, 广东揭阳人, 在读硕士研究生, 主要研究方向: 数论. E-mail: 675070711@qq.com
曹炜(1974-), 男, 湖北潜江人, 博士/教授, 主要研究方向: 数论与密码学. E-mail: caowei@nbu.edu.cn
(责任编辑 史小丽)
