海上救援应急线路评估分析算法
2022-03-16杨晓环杨卓超揭婉晨
杨晓环, 杨卓超, 揭婉晨
(1.中远海运科技股份有限公司,上海 200135; 2.舟山海事局,浙江 舟山 310005;3.浙江树人大学 管理学院,杭州 310015)
0 引 言
近年来,随着海洋经济的快速发展,我国海上各类型船舶数量持续增长,海洋资源开发等涉海活动越来越多,规模越来越大。据浙江省海上搜救中心统计:与“十二五”末期相比,“十三五”期间辖区内海上险情、遇险船舶和遇险人员数量均大幅度增加,分别增加16.5%、42.1%和22.2%;2019年,辖区内沿海水域共有227艘次船舶发生水上交通险情,遇险人员2 423人,引发事故110起,死亡和失踪45人,沉船39艘,直接经济损失达10 342.13万元。在这些事故中,一般等级和一般等级以上的事故数占全国水上事故总数的13.9%,死亡失踪人数占全国水上事故导致的死亡失踪总人数的18.9%,沉船数占全国沉船总数的24.3%。涉海业务的蓬勃发展使得我国的海上搜救任务日益复杂、繁重,搜救船舶驾驶员通常需面对很多环境方面的复杂情况。若要成功完成海上搜救任务,需依靠险情处置方案进行科学决策:快速定位、寻找失事船舶和落水人员,这是实施搜救计划的基础;快速抵达搜救区域,这是实施搜救计划的关键。但是,在实际搜救过程中,由于时间非常紧迫,需在搜救开始之前迅速利用信息系统制订出安全、准确、快速的处置方案(包括搜救线路);同时,由于搜救目标是不断移动的,需能利用信息系统实时规划最新航线,从而保证搜救力量快速抵达搜救区域,大大减轻船舶驾驶员定位和制订航线计划的负担。

图1 海上救援应急线路评估分析算法流程图
在设计航线时,一般需根据电子海图上的水深、障碍物和船舶参数等信息,将目标区域划分为碍航区域和可航区域。在可航区域内采用智能搜索算法寻找最优路径,即在己知被搜救船舶的准确位置和周围障碍区域的环境信息的情况下,寻找一条从起点到终点的满足要求的尽可能短的航行路径,使搜救船舶在通行过程中能安全可靠地避开所有障碍物。在对搜救船舶航行路径进行智能规划时,应同时考虑经济性和安全性。
海上救援应急线路评估分析算法流程图见图1。
1 环境建模
航线设计的基本原则是遵守海上通航规则,充分避开碍航物,获取能耗最少、路径最短和航行效率最高的航线。影响海上通航的基本要素主要包括初露水面的礁石群、岛屿、海上油田、桩标船和灯标等。 其他碍航区影响通航的要素还包括低于船舶净空高度的空中电缆和桥梁、军事演习区、垃圾倾倒区、弹药倾倒区、抛泥区和雷区等。此外,必须遵守内河船舶定线制的要求,将碍航区处理成符合船舶定线规则的区域。因此,在设计航线时,首要工作是对船舶所处的环境进行合理描述,即进行环境建模。
1.1 栅格法
栅格法是利用地图建模的一种方法,用栅格表示环境。栅格法实质上是对划定的地形图进行单元分割,使用大小相等的方块划分环境空间,并用栅格数组表示环境,比如用桔色表示障碍物,用浅灰色表示自由空间。对于混合栅格,根据自由空间和障碍物的占比将其归属于自由空间障碍物空间或自由空间,最短路径就是通过在该栅格图上搜索自由空间得到的。因此,栅格大小的选取是影响规划算法性能的一个很重要的因素。若栅格较小,虽然由栅格地图表示的环境信息会非常清晰,但需存储的信息较多,存储空间需求较大,同时干扰信号较多,规划速度较慢,实时性得不到保证;若栅格较大,虽然信息存储量较少,抗干扰能力较强,规划速较快,但环境信息划分较为模糊,不利于有效路径的规划。因此,在确定栅格大小时,存在求解进度与时空开销之间的矛盾。

图2 栅格数据单元分割示例
在处理浙江海域地图时,选取120°E~124°E,27°N~31°N的区域作为研究对象,采用栅格法进行地图建模。为更清晰地表示环境信息,将整个地形图单元分割成4 800×4 800的地形图,每个单元格的长度最大90 m,从而将整个地形图精准地表示出来。图2为栅格数据单元分割示例。
采用栅格法建立的浙江海域地形图见图3,其水深热力图见图4。
1.2 单元树法
在采用栅格法存储数据时,存储每个单元格的经纬度和水深点信息,存储文件大小超过500M。为减少存储文件,在得到栅格数据之后,采用单元树法对其进行处理,从而可将存储文件的大小减到4M以内。
单元树法正是为克服栅格法的缺点设计的,能有效避免时空开销与求解精度之间的矛盾。该方法根据浙江海域的水深将整个环境空间分成较大的单元格,即将栅格单元合并成大的单元格,满足各个大单元格的水深是相同的,从而将环境空间划分成不同大小的单元格。

图3 浙江海域地形图
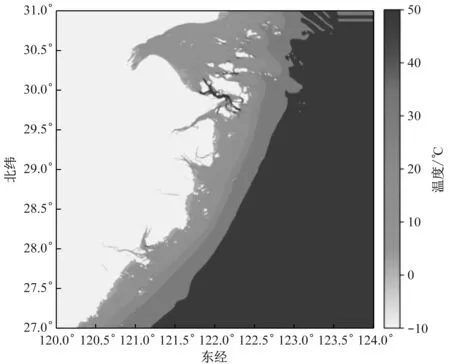
图4 浙江海域水深热力图
在二维空间内,单元树法又称四叉树法,其基本思想是将平面拆分为4个子平面,这些子平面仍可继续拆分。拆分得到的每个单元占用的空间可能是全为海域、全为陆地和混合型区域(既包含海域,又包含陆地)等3种情况中的1种。对于混合型区域,按前面的方法继续进行拆分,直到整个区域都是海域或陆地为止。该方法的优点是自适应性较好。以某海域数据(见图5)为例,采用单元树法对其进行分割,结果见图6。

图5 海域数据示例

图6 单元树法分割示意
2 无向连通图构建
参照单元树法,在构建连通网络时,取每个单元区域的中心点作为整个连通网络的顶点。每个单元区域的中心点都可与其相邻的单元区域的中心点相连接,从而完成对整个连通网络的构建。图7为单元树法分割结果;图8为连通图构建结果。
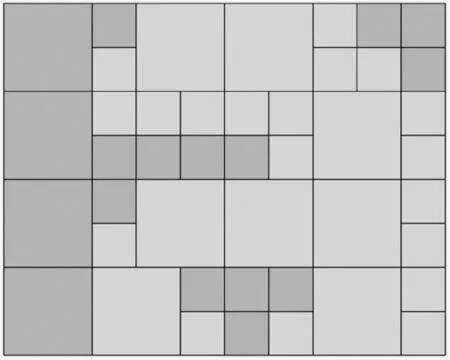
图7 单元树法分割结果
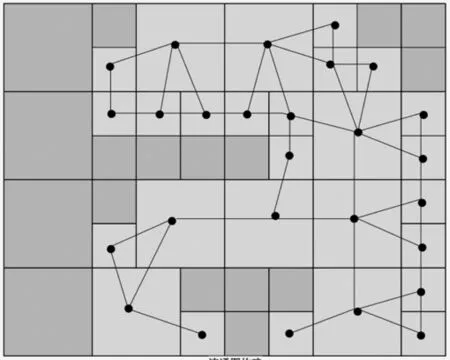
图8 连通图构建结果
将该方法应用于浙江海域,得到该海域连通图及其局部放大图,见图9和图10。
3 航线设计算法
3.1 基于弧的数学模型
在无向图=(,)中:为所有点的集合;为网络中所有弧的集合。用表示从点到点的距离;用点表示起点;用点表示终点。
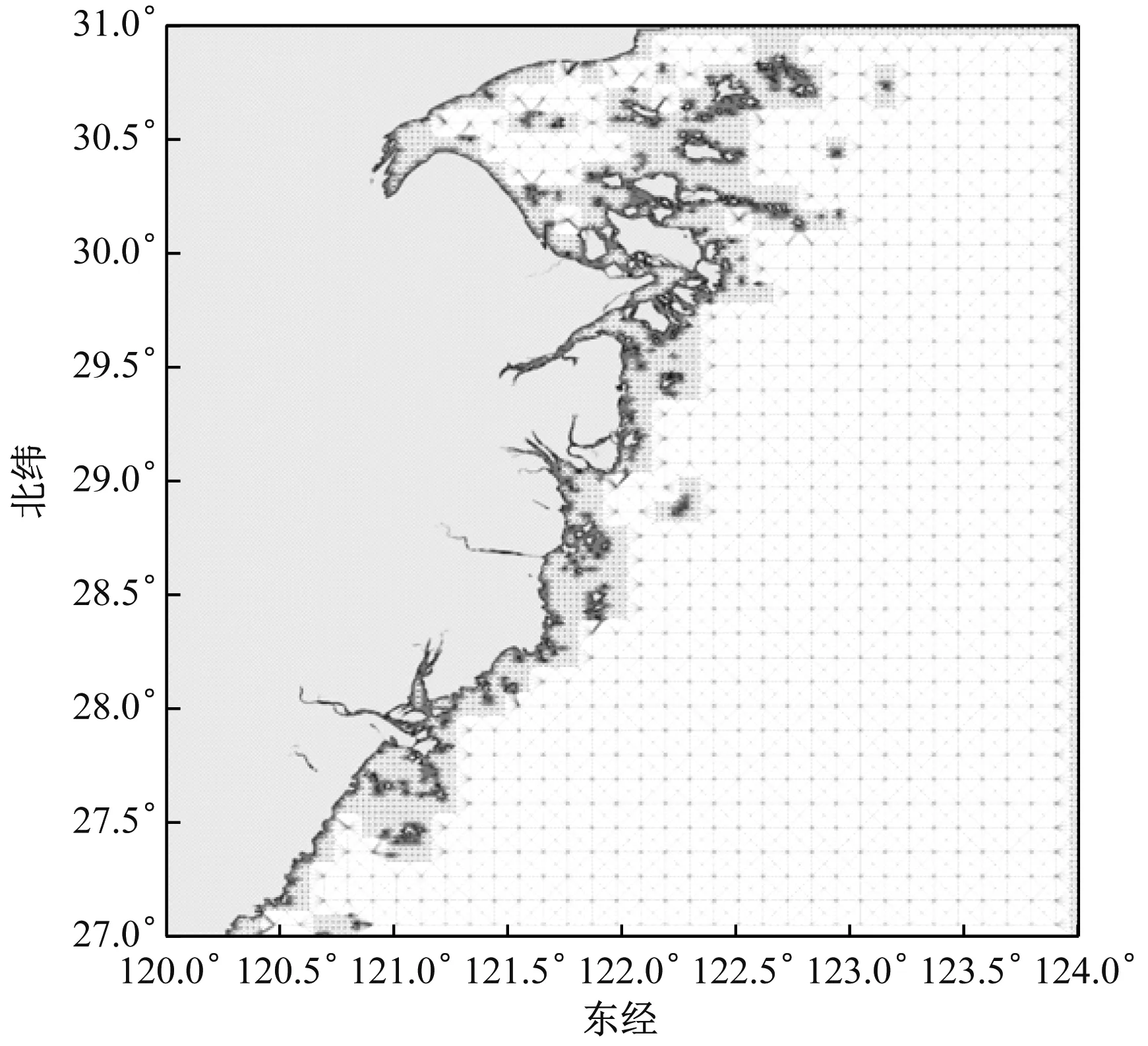
图9 浙江海域连通图
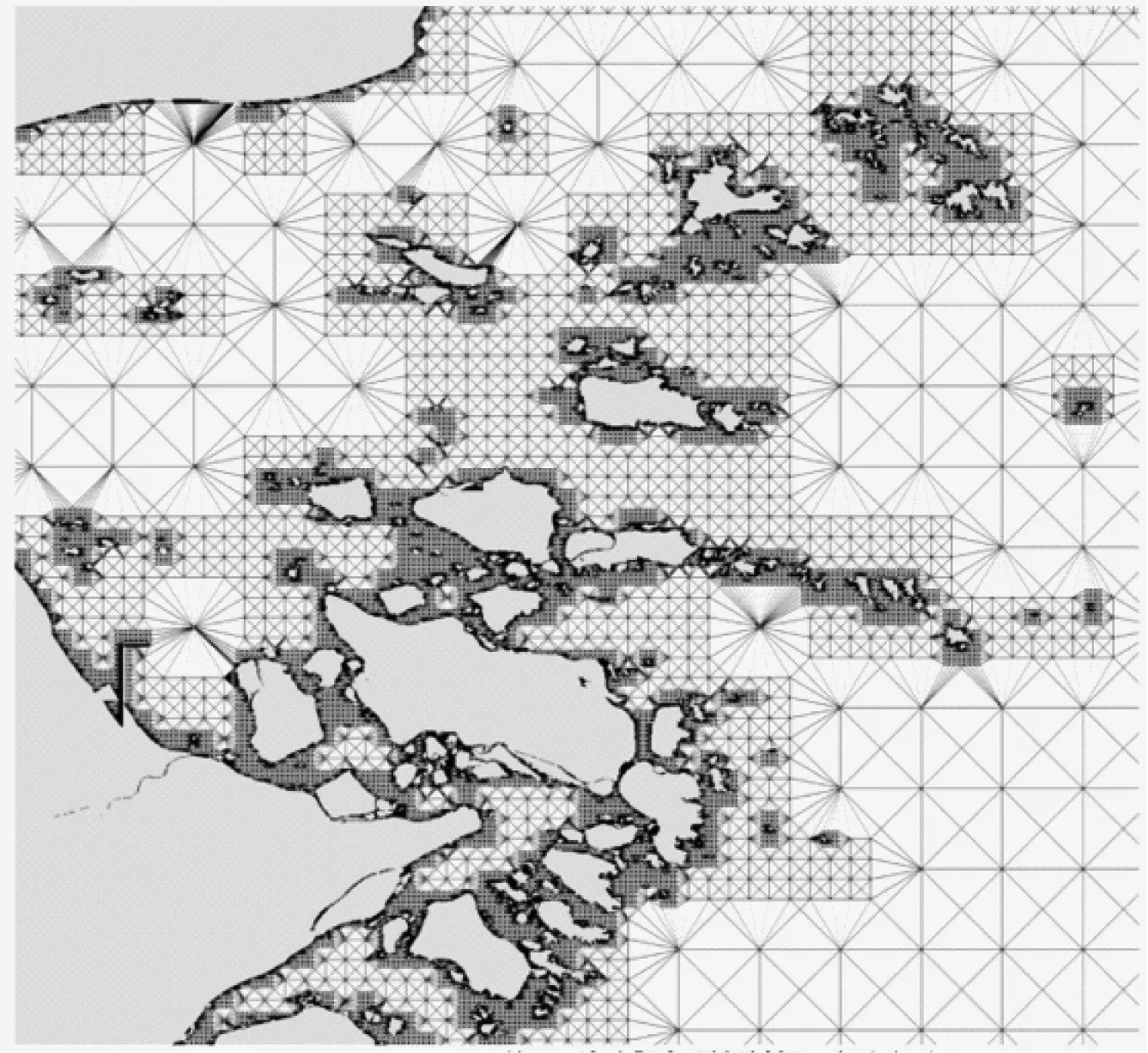
图10 浙江海域连通图局部放大图
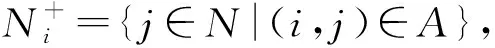
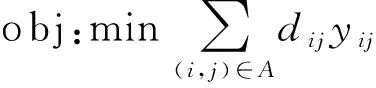
(1)
s.t.
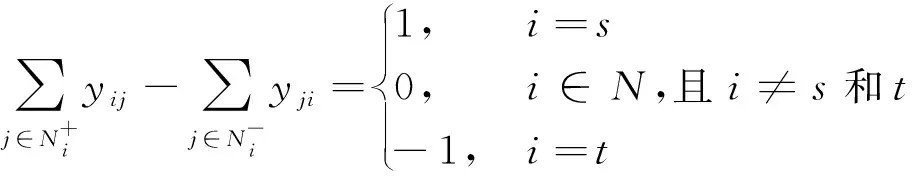
(2)
=0或1, ∀(,)∈
(3)
3.2 CH算法
CH(Contraction Hierarchies)算法是一种用于查找图形中最短路径的加速技术,可充分利用代表海上网络的图的特性,包括路网预处理和查询2个阶段。由于网络很少更改,可先进行一些计算(几秒钟到几小时),再进行查询,查询时间可达到毫秒级。CH算法依靠“shortcuts”实现这种加速。“shortcuts”线段连接2个不相邻的顶点和,其边权重是最短-路径上边权重的总和。
3.2.1 预处理
通过预处理能生成一个多层的结构,每个点都处在单独的一层。事先对点进行优先级排序,排序的好坏直接影响到预处理的效率和搜索的效率。首先,点的优先级(高低)可根据问题的特性调整,本文采用将相邻单元区域的中心点相连接的方式组建网络,邻接点个数最多不超过8个,且无特殊区域和特殊连接关系,因此网络中边的权重根据中心点之间的球面距离得到,优先级权重是边权重的累加值。其次,根据优先级由低到高依次选点进行收缩,生成“shortcuts”。接着,通过在预处理阶段创建的“shortcuts”减小搜索空间。最后,在最短路径查询中使用这些“shortcuts”跳过“不重要的”顶点,从而提高搜索效率。为达到该目标,需执行迭代式的顶点收缩。通过1次“收缩”1个节点预处理图形。为执行收缩操作,计算出节点之间的最短路径,并为其插入“shortcuts”,随后将节点标记为“已处理”。
这里用一个简单的图形说明节点收缩前后的状态,见图11。为收缩C,插入从A到E和从A到B的“shortcuts”,因为A→C→E和A→C→B为最短路径。不需要插入从B到E的“shortcuts”,因为B→C→E不是从B到E的最短路径,B→D→E较短。
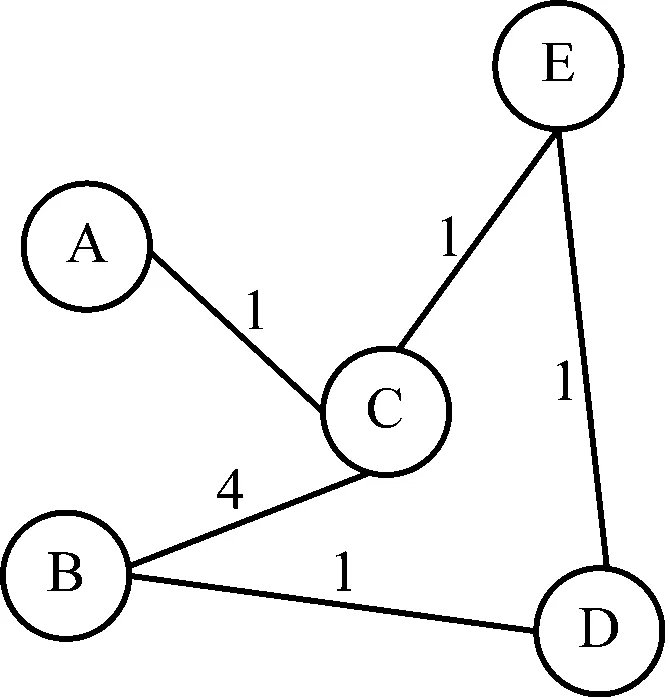
a) 收缩前状态
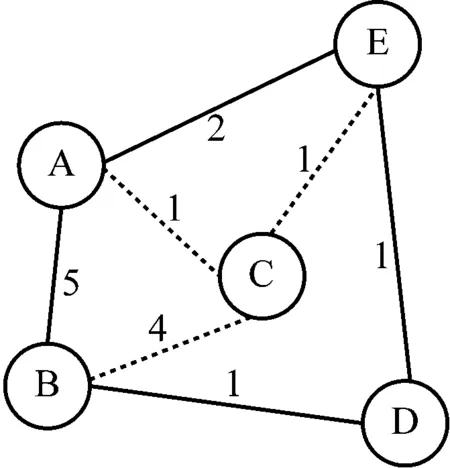
b) 收缩后状态
收缩并不是完全删除节点,在其他收缩过程中可忽略该节点,因为当看到一条通向C的边时,知道存在一条捷径,该路径可能不是一条最短路径。无论采用哪种方式,都不需要访问C。若进行以C开头或结尾的搜索,仍可找到该节点。
CH采用双向迪杰斯特拉(Dijkstra)算法,在搜索过程中,只能从级别低的地方向级别高的地方搜索,两边相遇之后就会保存途径路径。节点收缩排序的方法是使用优先级队列,该队列中的最小元素保存为最有收缩潜力的节点。
node收缩的顺序可用以下指标确定:
1) 边的差分(Edge Difference,ED)。ED可认为是最重要的node收缩条件,其计算公式为
ED=node_degree-number_of_shortcuts
(4)
式(4)中:node_degree为连接到节点的边的数量;number_of_shortcuts为删除节点之后必须创建的shortcuts数量。ED值越大,越先收缩。
2) 均匀度(Uniformity)。仅使用ED会获得相当慢的路径规划速度。应以均匀的方式收缩图中所有位置的节点,而不是将收缩节点保持在较小的区域内。
3) 收缩成本(Cost of Contraction)。收缩的一个耗时部分是前向最短路径搜索,用于确定“shortcuts”的必要性。 因此,可将搜索空间大小的总和看作优先项。
3.2.2 寻路过程
在查询阶段,从原始图上的起始节点和目标节点开始双向搜索(见图12),并通过预处理阶段创建的“shortcuts”进行扩展。为找到2个节点之间的最短路径,执行2次搜索,一次从起始节点开始搜索,一次从结束节点开始搜索,看二者在哪里相遇。搜索过程与Djikstra算法相似,但有一项额外的规则,即仅搜索收缩优先级比当前节点高的节点。在可视化中,这意味着仅搜索向上倾斜的边。
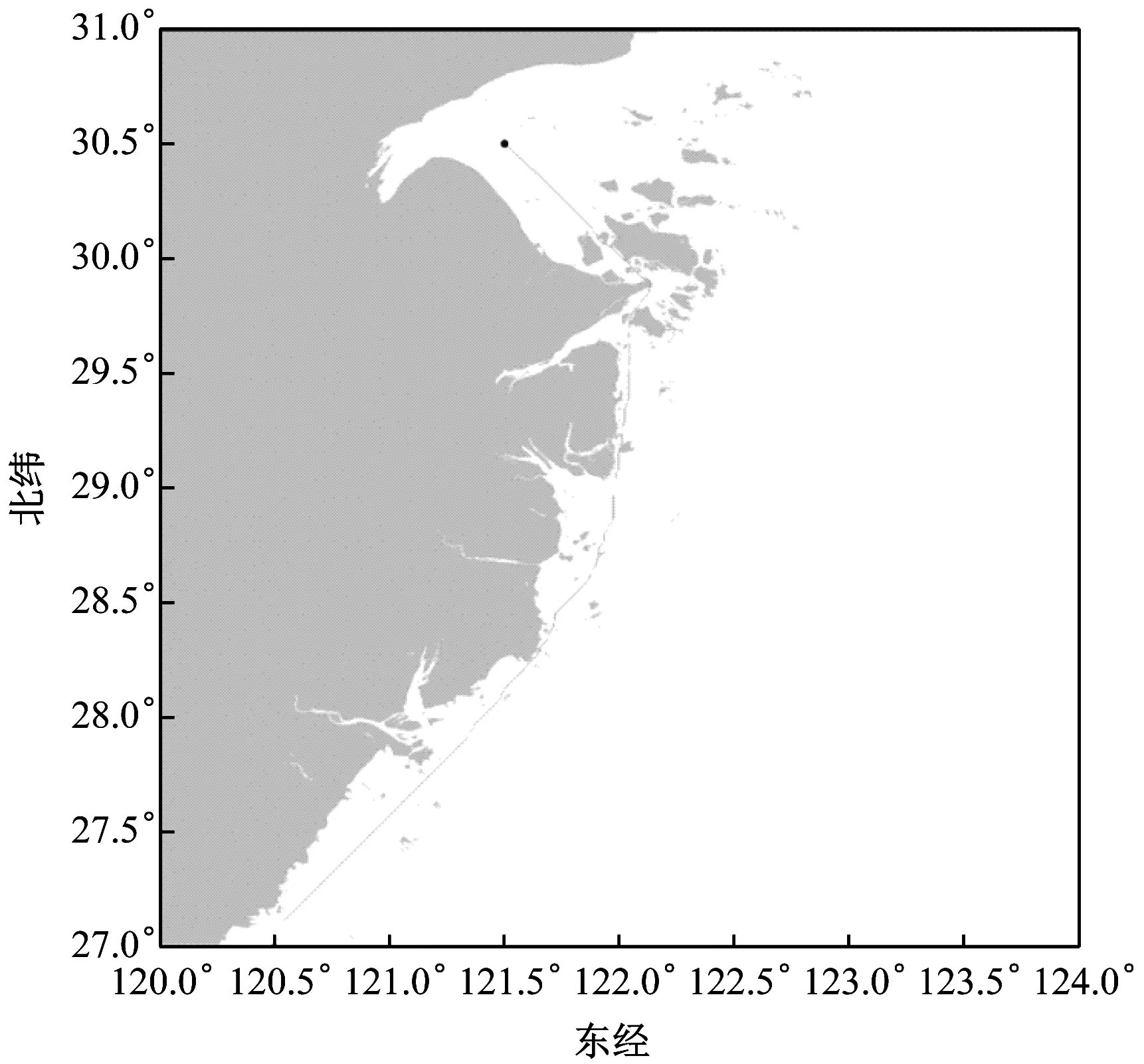
图12 在浙江海域求取的2个节点之间的最短路径示意
经纬度距离的计算公式为
=·arcos[cos·cos·cos(-)+sin·sin]
(5)
式(5)中:为经纬度距离;和为2个节点的纬度;和为2个节点的经度;为地球半径。
3.3 平滑处理
采用上述方法生成的航线会有很多不平滑的线段,具体见图13。 需对该线段进行处理,通过删除航线上的某些点,判断新的航线是否成立和距离是否缩短,由此更新航线。平滑处理过程如下:
While 新的航线比上一个航线更优(即距离更短)do
for all 线路顶点 do
if 某个顶点的相邻2个顶点的直线不经过障碍物
and 2个相邻顶点之间的距离小于通过该点连接2个相邻顶点的距离 then
去掉该顶点,生成一条新的线路
end if
end for
end while
经过平滑处理的路径图见图14。扩大生成的浙江海域局部图中的最短路径见图15。

图13 未经平滑处理的路径图
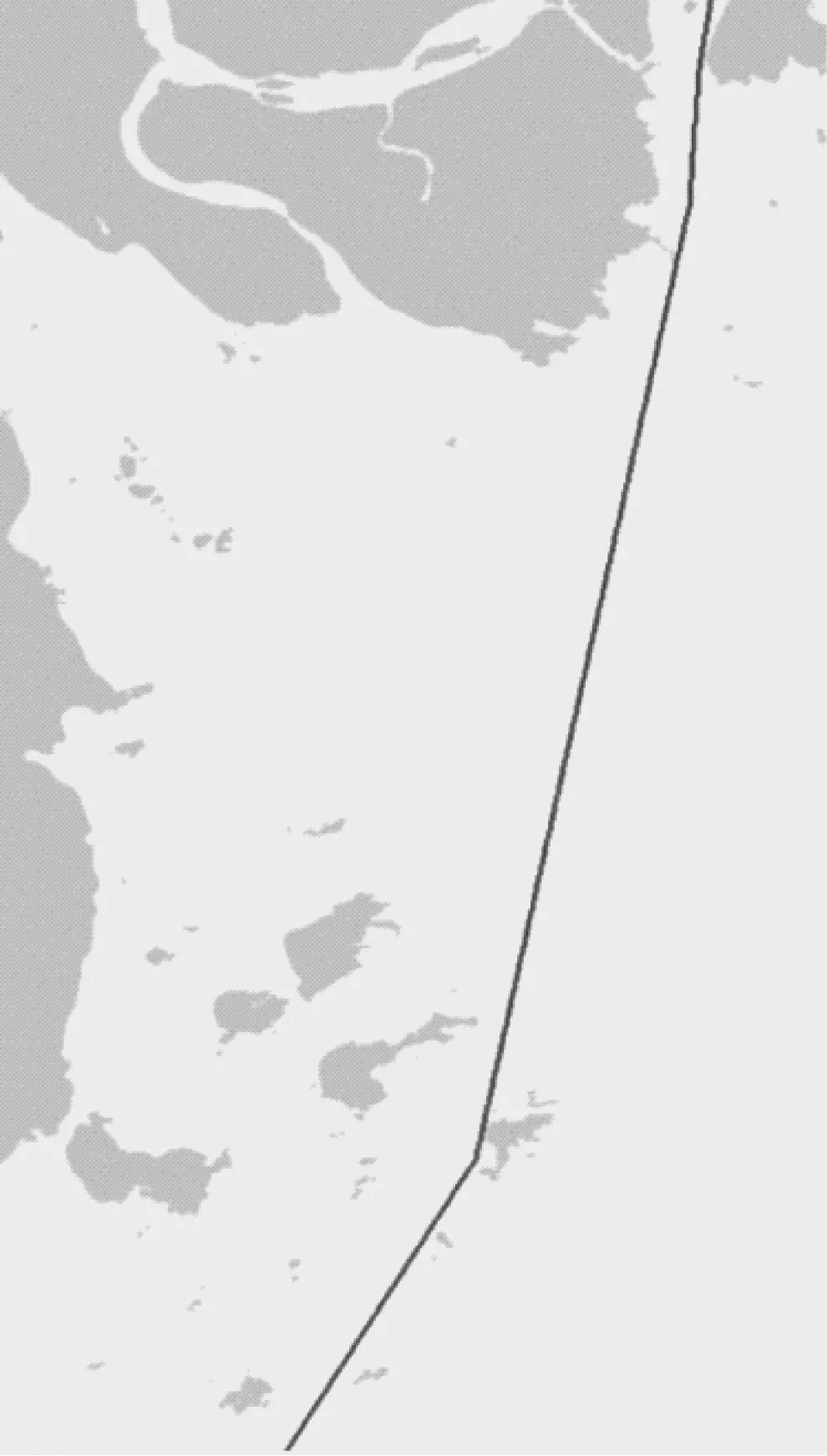
图14 经过平滑处理的路径图

图15 扩大生成的浙江海域局部图中的最短路径
4 实际应用效果
该算法已在浙江海事海上智控项目中得到应用,主要用于完成浙江海域的海上应急搜救,在收到参与险情搜救的指令之后,根据该算法为每艘应急搜救船生成推荐航路。
以保安事件恒利168险情为例,采用栅格法和单元树法对浙江海域数据进行处理,结果见表1。采用栅格法处理之后,生成14 622 988个格子,每次读取数据需要25.00 s;采用单元树法对采用栅格法处理的单元格进行处理之后,生成84 787个格子,每次读取数据只需要0.38 s,数据存储数量和读取时间显著减少。

表1 2种数据处理方法的数据处理结果对比
为测试CH算法在应急搜集场景下应用时的性能,通过筛选事故点周围3 n mile范围内的船舶(共计213艘),对该算法与传统的Dijkstra算法的数据读取时间进行对比,结果见表2。由表2可知,CH算法相比Dijkstra算法在数据读取时间上的性能显著提升。

表2 2种算法在应急搜集场景下的数据读取时间对比
为提高搜救线路的可行性,对算法计算结果进行平滑处理,并将所得结果与平滑处理前的数据相比较,结果见表3。由表3可知,经平滑处理之后,搜救线路途经顶点数量显著减少,航行距离缩短。
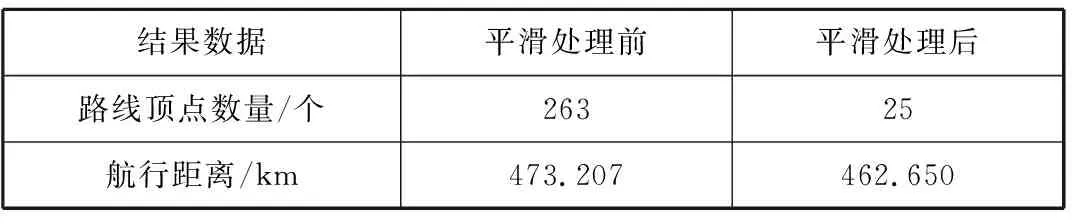
表3 平滑处理对比
平台运行实测:
1) 确定险情经纬度和船舶基础信息,发起算法。
(1) 参数为

(2) 发起的算法为
MarineLineRoutingDTO marineLineRoutingDTO=
algorithmFeignClient.marineRouting(marineLineRoutingRequestDTO)
2) 输出结果,共包含148个点,具体为
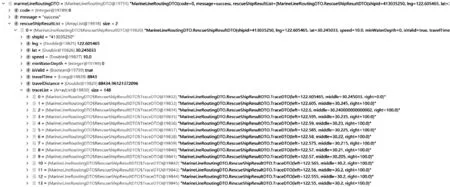
每个点的详情为
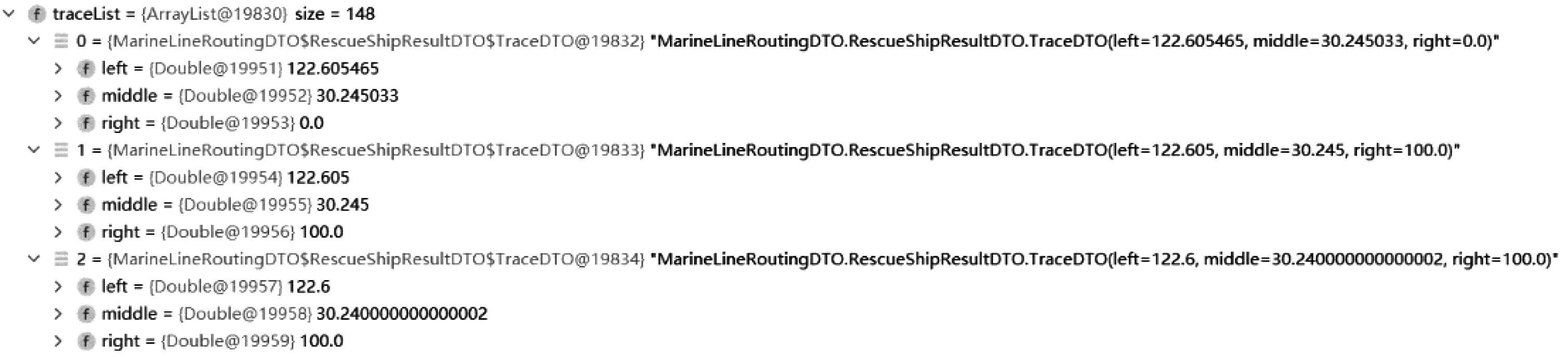
3) 将输出结果图形化(见图16),并对实际生产进行指导。
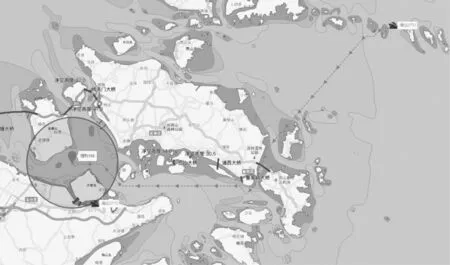
图16 图形化的算法输出结果
4) 显示其他计算路径,见图17和图18。
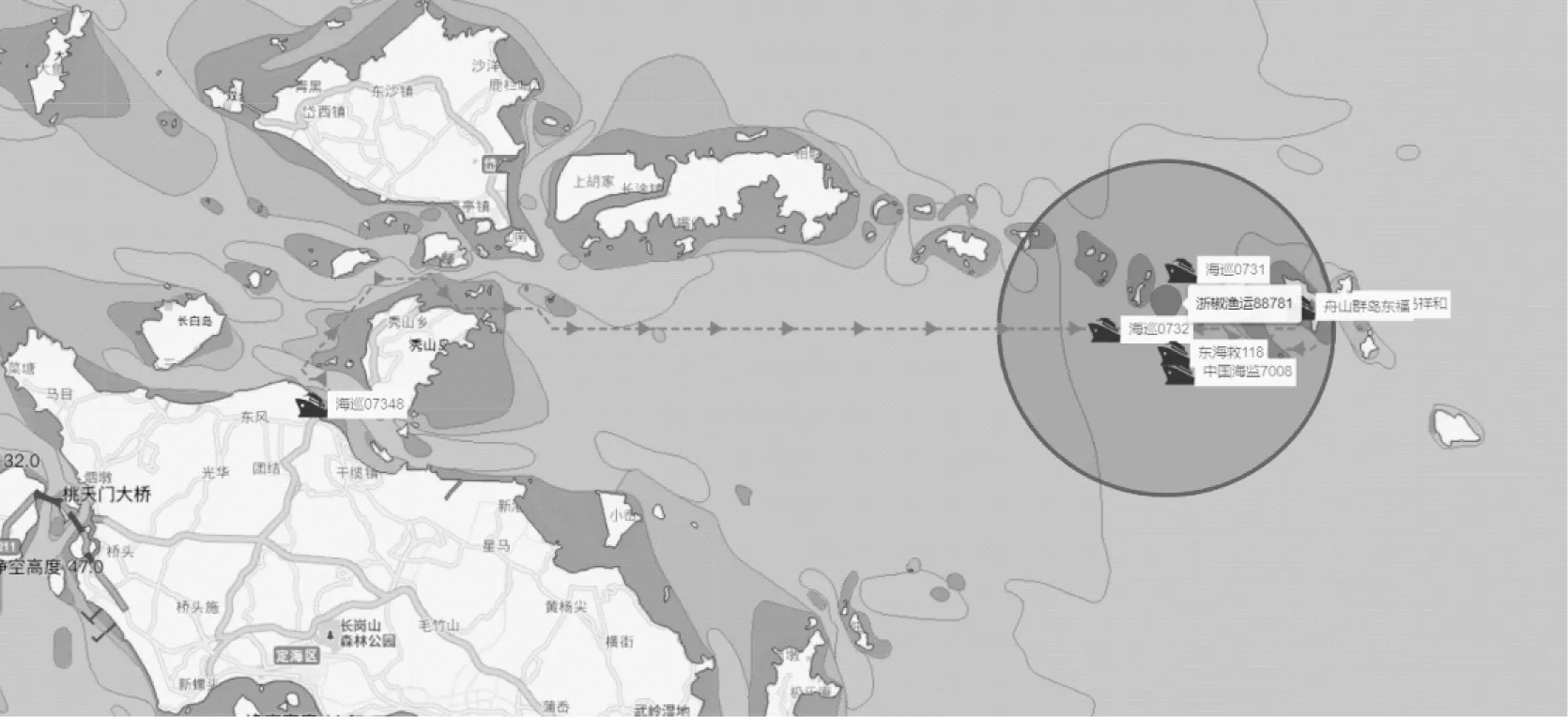
图17 显示的计算路径1

图18 显示的计算路径2
5 结 语
本文以浙江海事局辖区水域为例,采用数学方法对海上搜救路线进行了分析,设计了评估分析算法,并对该算法进行了实际应用。通过1个月的实践检验,证明采用该算法生成的最优航路具有较高的参考价值。该算法虽然已得到实际应用,且证实对应急险情具有实际帮助,但还存在一定的不足,例如有些无数据支撑因素(如渔船网位仪、潮汐)和无规律变动因素(如风速、船长习惯航路)没有考虑,后续将根据数据源引入进度在模型中逐步叠加相关因素,针对无规律变动因素建立经验库,引入相关硬件设备形成数据支撑,最终使推荐的最优航路更加精准。
