某集装箱船船型参数敏感度分析与阻力预报

王 策， 陈伟民， 杜云龙， 张青山

(1.上海船舶设备研究所, 上海 200032;2.上海船舶运输科学研究所 航运技术与安全国家重点实验室， 上海 200135)

0 引 言

近年来，随着国际海事组织(International Maritime Organization，IMO)对环保的要求日益严苛，绿色船舶的发展得到了越来越多人的关注，如何在保证船舶的安全性和经济性的基础上实现有效的节能减排，加快船舶线型优化的创新发展，已成为当今船舶科学领域重点研究的课题。

随着计算机技术和计算流体力学(Computational Fluid Dynamics，CFD)技术的不断发展，研究人员开发出了一套基于仿真设计的现代船型优化方法。该方法主要结合船型变换技术、基于CFD的船舶水动力性能评估技术和最优化求解技术，将水动力性能作为目标函数，将一些关键的船型参数和主尺度要素作为设计变量，采用多种船型变换技术改变局部或全局的船体型线，并计算船舶受到的总阻力，最终通过最优化求解技术计算得到符合船舶所有人要求的最佳船型。

然而，开展基于CFD技术的水动力性能计算需耗费大量计算时间和计算资源，这对船舶的设计成本提出了较高的要求。如何使船型优化方法更加智能高效，成为了船型优化领域重点考虑的问题。将人工智能算法引入船型优化工作中，是当前解决该问题比较好的方式。采用敏感度分析与机器学习模型相结合的方式预报阻力，不仅能准确、合理地降低设计空间维度，而且能在计算资源较少的情况下实现高效的船舶阻力预报，进一步推动船型优化的智能化发展。

采用敏感度分析方法能有效获取各设计变量对目标函数的影响程度，从而在工程设计中根据敏感度分析结果简化设计流程，大大提高工作效率。该方法在船舶工程领域，尤其是在船型优化领域的应用起步较晚，近年来有关研究逐渐增多。例如：DELENNE等采用敏感度分析方法对一维水动力模型进行了计算；STÜCK等采用基于雷诺平均方程的敏感度分析方法对通用集装箱船体进行了优化设计，提高了船尾流场的质量；KIM等基于三自由度操纵方程，在每次仿真中都计算稳定性指标和操纵性指标，采用灵敏度分析方法分析了船舶附体对DTMB5415舰船操纵性的影响，分别建立了2个回归方程描述操纵性与稳定性的关系和稳定性与船舶附体的关系，并优化了螺旋桨和舵的线型；张恒等采用径向基神经网络(Radial Basis Function,RBF)模型进行了阻力计算，并采用回归分析方法确定了棱形系数改变量和浮心纵向位置改变量等6个船型参数对船舶阻力性能的影响大小排序；ZHANG等以一组相似的集装箱船为研究对象，采用偏最小二乘回归分析法分析了局部特征参数对船舶阻力性能的敏感度；LIU等采用基于Kriging模型的TPBF(Tensor-Product Basis Function)方法和改进的Sobol’s方法进行了船型优化，确定了各变量的影响程度，排除了影响较小的变量，实现了设计降维，验证了计算、优化和回归结果的精确性；陈佳宝等基于泰洛系列剩余阻力系数图谱，采用回归分析法对不同航速下的棱形系数、排水量长度系数和宽度吃水比对剩余阻力系数的敏感度进行了分析，得出了各参数对剩余阻力的敏感度指数，并验证了已知船型参数对船舶阻力的影响。

此外，有很多学者将机器学习算法和代理模型应用到船型优化中。例如：EKINCI等基于114艘油船的营运数据，采用多种机器学习算法预报了油船的主要设计参数，取得了较好的预报效果，通过比较得出模型树算法是该案例中预报精度最高的算法；BABADI等基于高速和半滑行状态下的耐波性数据，采用BP(Back Propagation)神经网络分析了水线面系数和棱形系数对船舶耐波性的影响，结果表明，增大船舶前体可改善甲板砰击，船舶横摇幅度与整体呈正相关关系；LEE等以某4 300 TEU集装箱船为例，结合神经响应面与非支配排序遗传算法优化了船体结构；肖振业等以国际标模KCS船型为研究对象，采用支持向量机模型和神经网络模型分别预报了船舶总阻力，通过对比分析发现，支持向量机的预报精度明显优于神经网络；侯远杭等基于在设计空间内选取的大量船型样本点，采用IPSO(Improve Particle Swarm Optimization)-BP神经网络建立了变形参数与兴波阻力的关系模型，并以不同航速下的船舶阻力加权和为目标，采用遗传算法和模拟退火算法对船型进行了优化；LIN等采用Kriging模型建立了双艉型船的船型参数与阻力值之间的数学关系，并通过多目标进化算法求得了最优解。

由上述研究可知，将代理模型技术应用于阻力预报和船型优化工作中，能在一定程度上解决单纯采用CFD技术进行优化求解耗费的时间和计算资源较多的问题。本文以一艘集装箱船为研究对象,对其进行船型参数敏感度分析和阻力预报。首先，根据经验和已有研究确定所要研究的船型参数及其变化范围，由于集装箱船需满足内部容量要求，船长和船宽的变化范围十分有限，故重点分析对阻力较敏感的球鼻艏和艉封板处的船型参数。其次，基于Sobol模型将该集装箱船变形为305艘船，利用Lanckenby变换和FFD(Free Form Deformation)变换等多种变换方法得到该船的优化船型。然后，基于CFD技术建立适用于该系列船的计算模型，并对这305艘船进行阻力计算。最后，基于计算和优化得到的结果，采用回归分析法对各参数和具有代表性的参数组合进行敏感度分析，根据分析结果对该系列船进行基于神经网络模型的阻力预报。在此基础上，采用穷举法得到该船的多种优化方案及其阻力性能数据库，定量描述各参数和参数组合对船舶阻力性能的敏感度，获得船舶阻力预报模型。该船型参数敏感度分析和阻力预报研究思路见图1。

图1 船型参数敏感度分析和阻力预报研究思路

1 基于Sobol算法的船型变换

研究船舶在18 kn航速下受到的总阻力，并基于Sobol模型对给定船型进行Lackenby与FFD组合变换。Lackenby变换又称1-C变换，主要通过改变母型船的横剖面面积曲线改变船舶的瘦削程度;FFD变换是指在需变形的局部区域设置格子，通过Bernstein多项式建立格子上的控制点与船体表面相应点之间的坐标联系。图2为FFD变形示意。

图2 FFD变形示意

选取浮心纵向位置、进水角、船尾横剖面面积曲线形状参数和船首横剖面面积曲线形状参数等9个船型参数作为敏感度研究的设计变量。由于集装箱船的型宽和船长的变化范围较小，故重点关注球鼻艏处和艉封板处较敏感部位的变形。所选船型参数的名称和物理意义见表1。

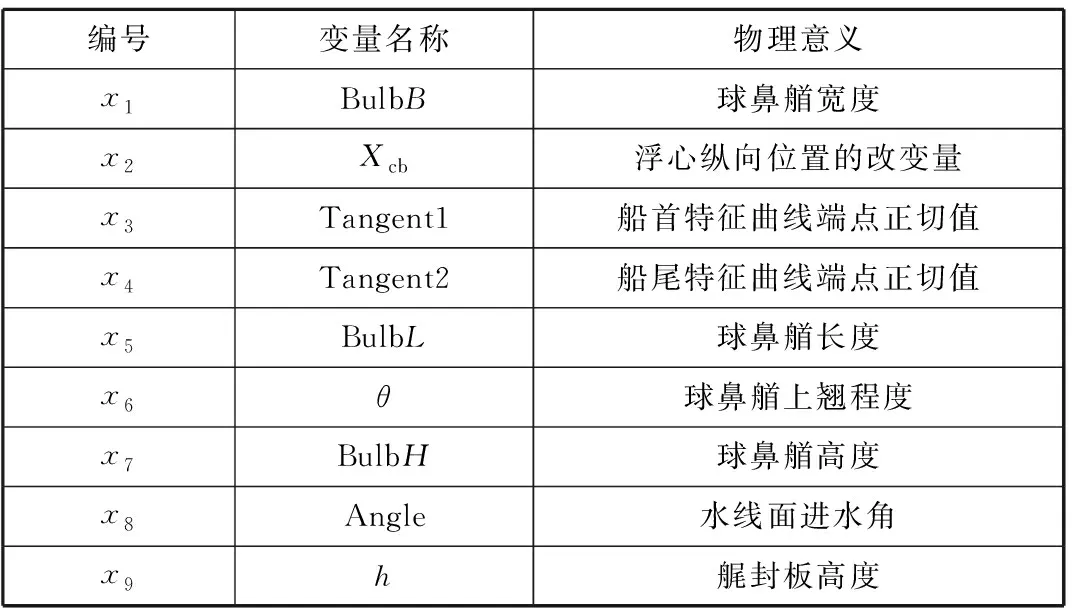
表1 所选船型参数的名称和物理意义

表1中，Tangent1和Tangent2对应的特征曲线在Sobol模型中是用来生成横剖面面积的曲线,直接影响横剖面面积曲线两端的形状，即影响船首和船尾的形状。球鼻艏处格子中控制点基础改变角度θ取不同值时球鼻艏变形示意见图3。

基于以上3种变换，通过Sobol算法对原型船的9个变量进行计算，得到305艘系列新船和相应的静水力计算结果。同时，采用计算模型对这305艘新船进行阻力性能计算，保留每艘船的阻力计算结果和船型参数变量值，以便进行敏感度分析。

2 基于CFD的原型船阻力性能计算

采用模型试验与数值仿真技术相结合的方式确定该集装箱船在18 kn航速下的总阻力计算模型。通过

图3 艏处格子中控制点基础改变角度θ取不同值时球鼻艏变形示意

将数值仿真结果与模型试验结果相对比，确定精度最高的数值仿真结果，并保留仿真计算模型，以便采用该模型对通过Sobol变化得到的船舶进行阻力性能计算。

数值仿真方法主要有势流方法和黏流方法2种，其中：势流方法能较大程度地对实际流体问题进行简化，计算成本较低，但计算精度不高，且无法准确得到流场细节；黏流方法是指基于CFD的数值仿真方法，计算精度较高，能准确得到流场细节，本文选用该方法对原型船进行阻力性能计算。

在笛卡儿坐标系下进行阻力性能计算，对于黏性不可压缩流体，其流动规律主要遵循连续性方程和雷诺平均方程，其张量形式为

(1)

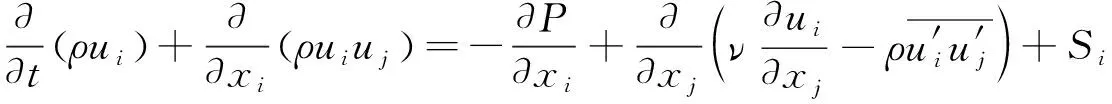
(2)

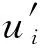
由于船型边界条件较为复杂，有限体积法相比有限差分法、有限元法和谱分析法具有高效处理复杂边界条件问题的能力，故在计算中采用有限体积法对模型进行离散。

本文中的湍流模型采用SST(Menter)K-Omega模型，有

(3)

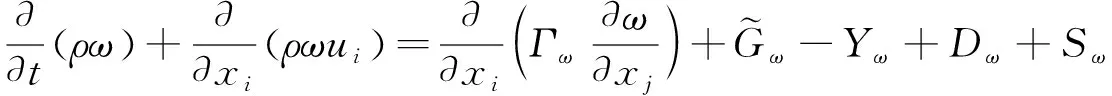
(4)

由于本文所述船舶是左右对称的，故只对船舶的1/2结构进行计算。计算外域的速度进口距离船首1倍船长，压力出口距离船尾2倍船长。通过布尔运算设置计算边界，为保证计算域中进口和出口处流动均为定常状态，将距离船首1倍船长处设置为入口，将距离船尾2倍船长处设置为出口。将船体中纵剖面设置为对称平面，向左的位置为计算外域壁面边界。将船体表面和计算域上下边界设置为壁面边界，边界条件为可滑移固壁条件，船体表面假设为不可滑移固壁条件，近壁面处利用壁面函数法处理，具体边界设置见表2。

网格划分和加密是CFD计算中的重要环节，网格过疏或加密不合理均不能得到准确的计算结果，网格过密会导致计算时间过长，计算成本过高。网格设置是在保证计算结果的精准度与节约计算时间成本之间寻找平衡的过程。本文共设置9个网格加密区域，其中，船体周围2个，开尔文波处2个， 自由液面处3个，球鼻艏处和船尾处各1个，具体见图4和图5。

采用壁面函数法对近壁面进行求解，在近壁面处设置边界层网格，采用近壁面第一层网格的厚度控制边界层网格的质量，第一层网格的厚度Δ通过无量纲参数控制，二者之间的关系为

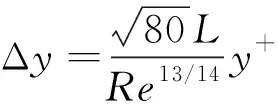
(5)

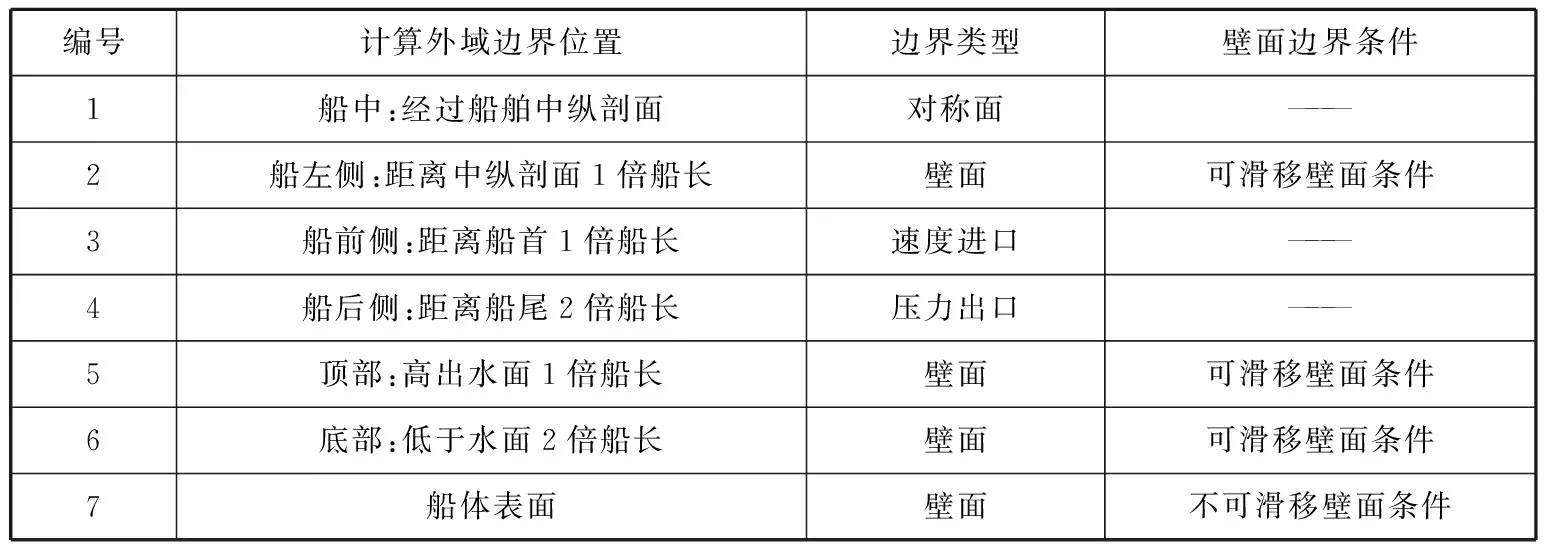
表2 边界设置

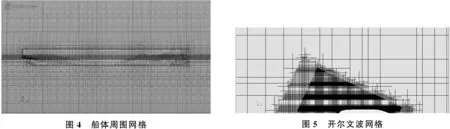
Re=UL/ν

(6)

式(5)和式(6)中：为船长；为雷诺数；为特征速度；为来流运动黏性系数。对于壁面函数法而言，一般要求 20<<100，由此可得到第一层网格厚度的合理范围，并根据计算结果在合理范围内调整第一层网格的厚度。

综上，非加密区域的网格基本尺寸设置为0.1 m，面网格增长率设置为1.3，棱柱层设置为5层，棱柱层总厚度设置为基本尺寸的40%，最大网格单元尺寸设置为相对基数的800%。

企业在其经营发展的不同时间段，使用的管理方式和协调方式也会存在差异。传统企业在开展经营工作过程中，经营者一般将经营的重点放在监督和协调上。利用全面预算管理开展各项管理工作，可以将程序化和制度化有效结合起来，推动企业审计、考核以及监督等各项工作全面开展，不仅有利于企业完善预算管理制度，也有助于推动企业实现进一步发展[1]。

通过计算得到，当计算航速为18 kn时，原型船船模受到的总阻力为13.833 93 N;通过阻力试验测算得到的船模受到的总阻力为13.708 80 N。根据误差计算公式可得到计算结果与通过船模试验测得的总阻力值相差1.4%，即

(7)

式(7)中：为阻力试验测算值;为CFD计算所得总阻力值;为误差。一般地，若误差在2%以内,可认为该CFD计算模型的精度满足要求，计算方案可行。

将该计算方案应用于第1节所述305艘船的变形方案中，得到这305艘船所受总阻力的取值范围为13685 62～16085 38 N。

3 船型参数对阻力性能的敏感度分析

敏感度分析又称敏感性分析、灵敏度分析，是定量描述各自变量在某特定范围内的变动对模型的影响程度的方法。假设模型为

=(,,…,)

(8)

令变量在可能的取值范围内变动，研究这些变量发生变动对值的影响程度。

敏感度分析方法可根据研究范围和变量变化个数分为局部敏感度分析和全局敏感度分析。由于本文研究的是第1节所述9个变量中的单一变量对船舶总阻力的影响和这些变量交互作用对船舶总阻力的影响，故选取全局敏感度分析中较常见的回归分析方法对船型参数对阻力性能的敏感度进行分析。

对原始数据进行无因次化和归一化等预处理之后，利用多种回归模型和方法对所选9个参数及参数组合的敏感度进行分析。得到回归方程之后，每个参数或参数组合的系数大小可定量反映对应的敏感度。对得到的方程进行可靠性检验，检验标准有多种，本文通过相关系数检验和均方根误差这2个判定指标判断分析所得回归方程的可靠性。

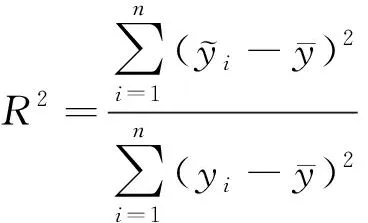
(9)

也是回归方程的检验标准之一，在回归模型中，真实值与预测值之差称为残差，全部预测值的残差平方和与原始数据组数比值的平方根称为。本文所述是逐步回归分析中变量引入和提出的重要标准之一。的计算公式为

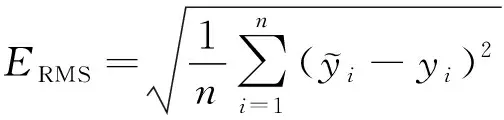
(10)

由于选定的9个变量并不是简单的单独影响阻力值，而是存在交互影响，故尝试加入二次变量，如交互项和平方项，采用多项式回归方法进行分析。回归模型选择由9个自变量组成的完全二次多项式，其表达式为

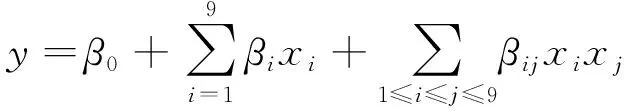
(11)

式(11)中:为常数项；为回归模型一次项(主效应)系数;为回归模型二次项(交互效应和平方效应)系数。

由于由9个自变量组成的完全二次多项式共有54个自变量项和1个常数项，自变量项较多，且自变量项与因变量的相关性未知，需要筛选，故采用逐步回归分析的方法，逐个引入自变量项，并对每次引入的自变量项进行拟合，保留影响显著的自变量，剔除影响不显著的自变量，通过比较的大小最终得到最小、拟合度最佳的回归方程。本文共进行107次回归，最终选择标准差最小的一组进行检验。图6为逐步回归历史残差图。

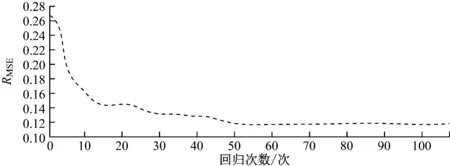
图6 逐步回归历史残差图

表3和表4为经过逐步回归拟合后各变量项的系数，其中:表3为一次项的系数;表4为二次项的系数，回归中得到的常数项为13832。

表3 回归模型一次项(主效应)系数βi值

检验时先通过相关系数对回归方程进行相关性分析，判别回归方程自变量和变量组合选择的合理性。通过计算得到=0.83,判定自变量与因变量显著相关，回归方程可靠。通过计算得到=0.116 71，标准差非常小，表明拟合效果很好。

由上述分析可知,本文计算所得回归方程均符合检验标准，说明所得回归模型可靠。

根据回归模型的计算结果，按敏感度大小(的绝对值)将各参数项分为影响相对较大、相对较小和影响极小等3类，并按敏感度大小对各参数项进行排序，分类依据见表5，分类和排序结果见表6。表6中:“影响相对较大”和“影响相对较小”2列中的各参数项按敏感度由大到小排列，从上至下，敏感度依次减小;“影响极小”一列的敏感度均近似为零，该列各参数项无排序。

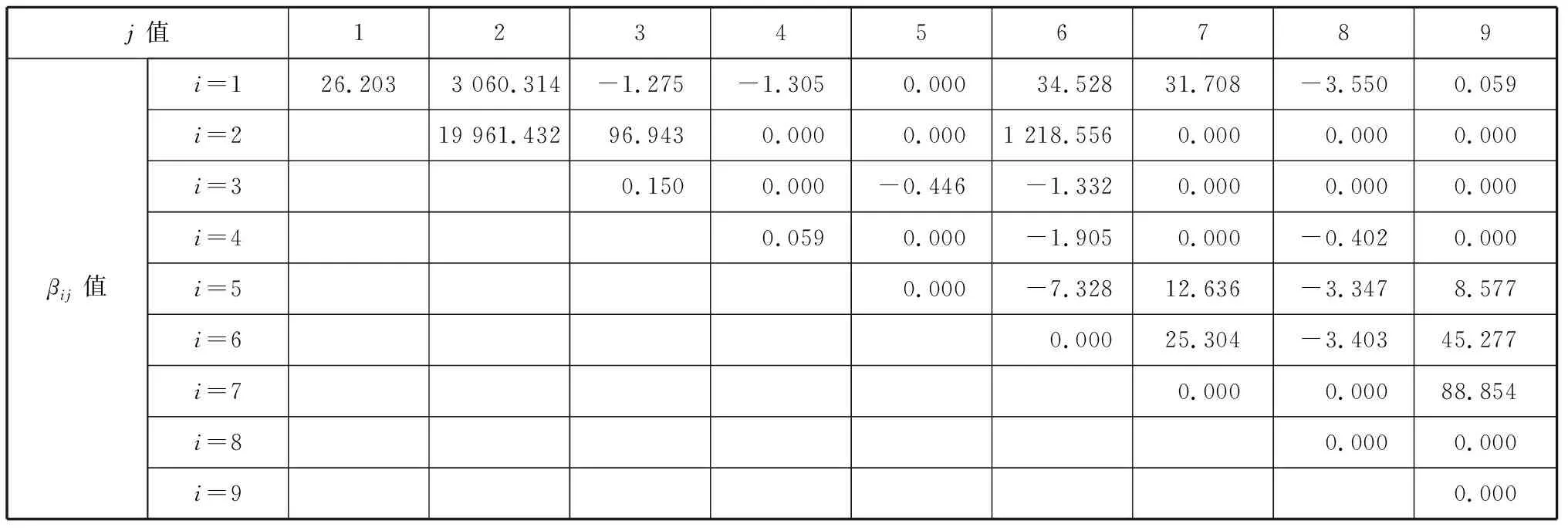
表4 回归模型二次项(交互效应和平方效应)系数βij值

表5 参数项分类依据

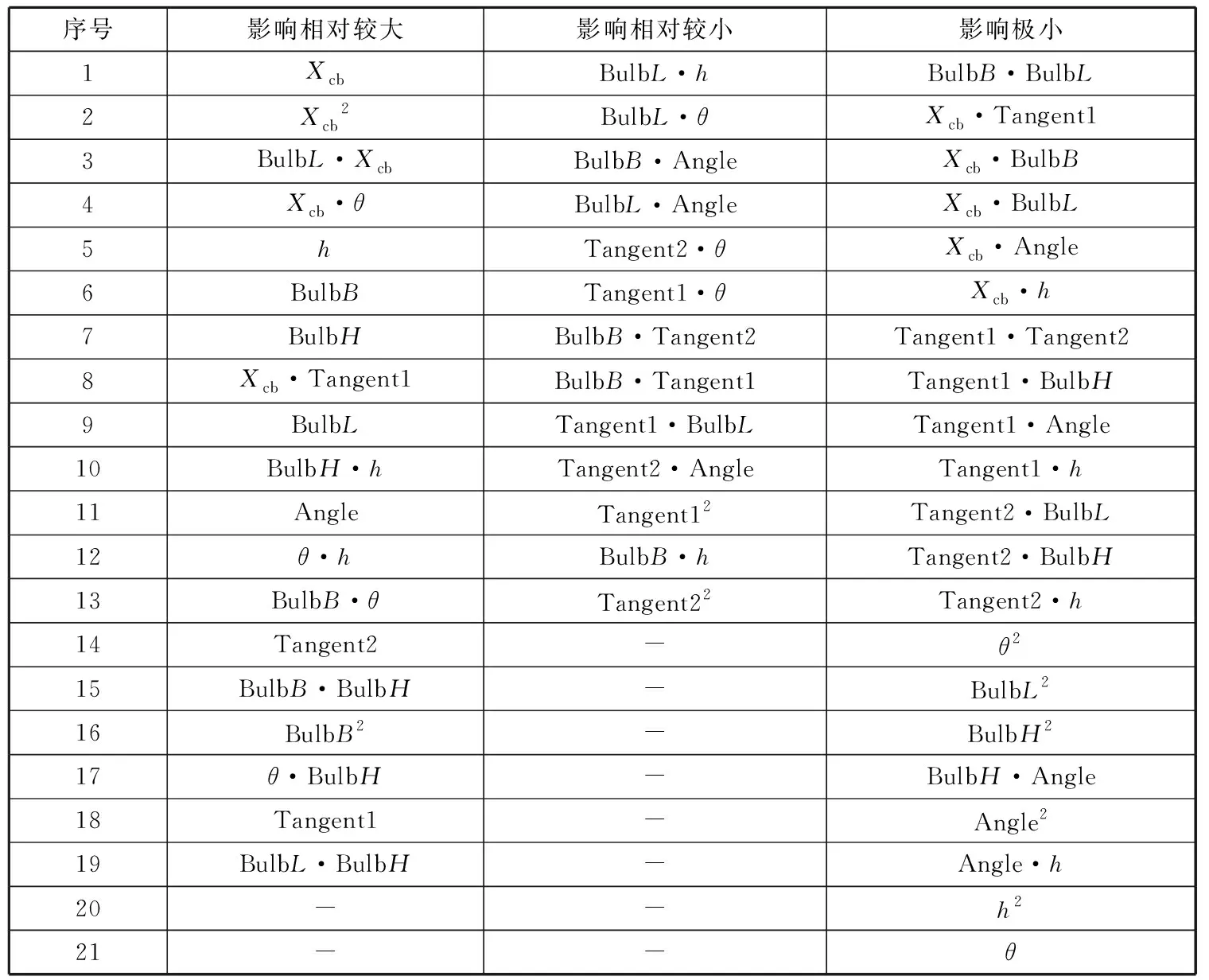
表6 各参数项分类结果

从表3～表6中可看出各参数项系数的敏感度大小排序，同时可发现：浮心纵向坐标位置及其平方项与部分组合在研究的特征参数和参数组合中对阻力的影响最大，与球鼻艏相关的参数(球鼻艏长度Bulb、宽度Bulb和高度Bulb)或参数组合对阻力的影响也比较大，与船舶型线设计经验相符。然而，船首和船尾特征曲线正切值虽然很大程度上影响着船舶型线形状，但其与阻力的关系经历了若干函数映射，并不直接影响阻力大小，多次映射削弱了船首和船尾特征曲线正切值对阻力的影响，故与它们相关的多个参数项对阻力的敏感度表现欠佳。

4 训练神经网络模型

由于神经网络适宜用来进行函数拟合，故本文基于神经网络算法训练阻力模型。采用双层前馈网络，将sigmoid作为隐藏层传递函数，输出层采用线性传递函数。隐藏神经元的默认数量设置为10个。将上述敏感度分析中保留的参数和参数项作为输入向量，将阻力作为输出向量进行拟合。数据分为训练集、验证集和测试集，分别占70%、15%和15%。

训练算法选用Levenberg-Marquardt，当连续迭代6次仍无法降低验证误差时，结束验证。

图7为神经网络拟合效果图，分别为训练集目标、验证集目标、测试集目标和全部数据集目标相关的网络输出，其中：Data为预测值；Fit为拟合曲线；=表示预测值等于真实值。在完美拟合情况下，预测值等于真实值；拟合曲线与=对应的虚线越接近，说明拟合效果越好。通过计算可得，训练集、验证集和测试集的值分别为0.89、0.68和0.59，全部数据集的值为0.78。

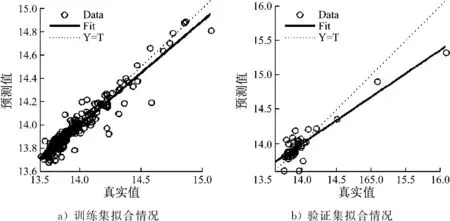
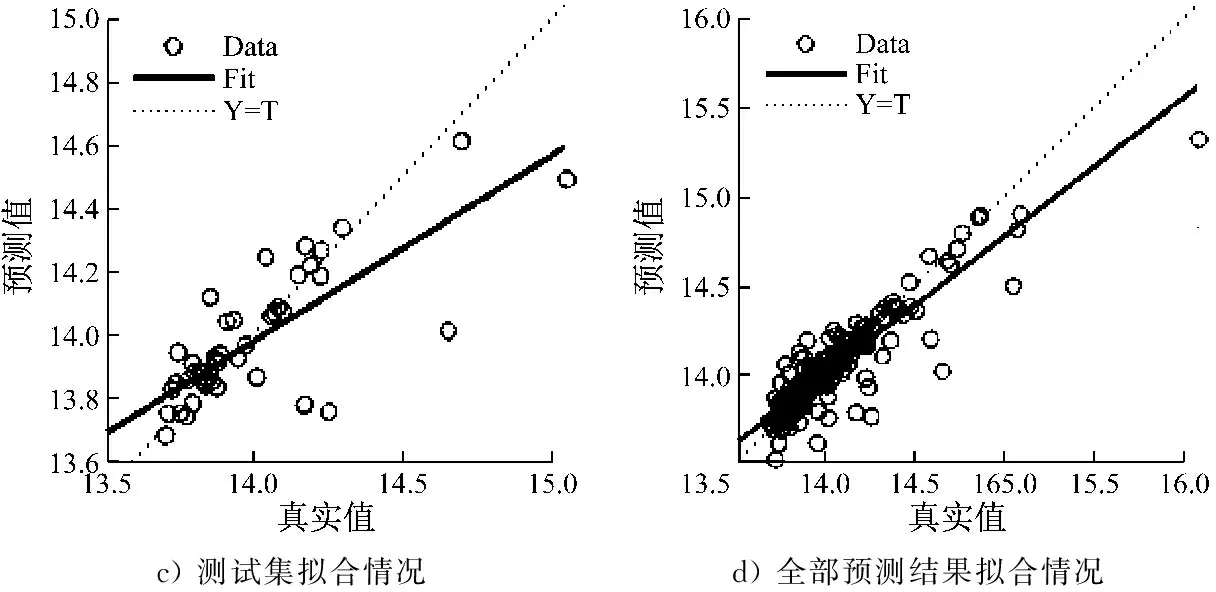
图7 神经网络拟合效果图

图8为误差直方图。由图8可知，在本文得到的训练模型中，误差主要分布在[-0.260 2,0.375 1]范围内,误差非常小，模型训练效果很好。

图8 误差直方图

5 结 语

本文定量地给出了与算例集装箱船接近的船舶各特征参数的敏感度，可删减敏感度系数接近0的参数，为后续船型优化工作中的降维简化提供参考。同时，基于神经网络建立了船舶阻力预报模型，为后续降低船型优化工作时间成本奠定了基础。本文选取的样本和船型参数的数量有限，回归模型的相关性和预报的准确性还有提升的空间，如何在时间成本较低的情况下得到较多的样本，如何更合理地选取船型参数和参数组合，是未来需解决的2个关键问题。

本文研究所得结果为智能优化系统开发奠定了很好的基础。后续，可在开展船型优化工作时建立各船型的数据库，利用本文研究所得结论，结合大数据分析与模拟技术，引入人工智能领域的深度学习方法，大大减少计算量，进一步推进船型优化的智能化发展。