基于最小二乘法的船舶电力监控系统数据压缩策略

王永臻

(上海船舶运输科学研究所 舰船自动化系统事业部， 上海 200135)

0 引 言

船舶电力系统是船舶的生命线，在保障电力推进、甲板机械、控制与通信等设备正常工作方面具有重要作用。大型船舶电力监控系统的网络拓扑通常采用2层结构设计，其中：上层网络采用冗余的高速交换式工业以太网，网络拓扑采用环形方式；下层网络主要采用双冗余CAN(Controller Area Network)现场总线网。现场监控设备采集的数据主要通过下层网络传递给网关，网关通过上层网络将数据传递给服务器，服务器将数据记录到数据库中。一艘大型船舶的测点有上万个，按每秒采集1次数据计算，每天产生的数据量有几十吉字节。根据实际需求，服务器需存储最近3个月内的监控数据，而船舶的数据存储空间有限，采集的数据必须先作压缩处理，再进行存储。近年来，为改变芯片、操作系统等核心软硬件主要依靠进口的现状，船舶设备国产化研究越来越受重视，而目前国内尚无满足需求的工业数据库，现有的国产数据库暂不能提供可靠的数据压缩技术，若直接将监控数据存入国产数据库中，会导致数据存储不及时，造成数据堆积，从而影响船舶电力监控系统的正常运行。因此，需设计一种数据压缩策略，先对监测的数据进行压缩，再将其存入国产数据库中，以满足船舶监控设备的需要。

数据压缩技术主要分为无损压缩技术和有损压缩技术2种，传统的无损压缩技术的压缩量较小，已无法满足当前船舶监控设备的需求。目前的数据压缩技术主要根据数据的特点，选择不同的压缩方法。文献[3]采用小波变换和嵌入式零树编码的方法压缩电力数据，先选取合适的小波基对数据进行小波变换，再通过嵌入式零树编码对经小波变换得到的数据进行压缩，该方法的压缩比较高，运算量适中，适用于电力系统录波，但在船舶电力监控系统中，由于采集数据的频率较低，若采用该方法，需先将数据存储一段时间，再对其进行处理，这会导致数据处理时间较长，内存消耗较大。文献[4]采用基于密度划分的数据存储方法，先将相近的数据纳入1个区域内，再去除冗余的数据，达到预期的压缩效果，这种方法可有效压缩地理信息类数据，但解压缩数据时算法较为复杂，且压缩率较高，不适宜监控系统采用。Wonderware工业数据库采用旋转门算法压缩数据，该算法原理简单，编程比较容易实现，但当数据在某一时间段内发生突变时，采用该算法压缩的数据会严重失真，若减小压缩误差，压缩率难以得到保证。

船舶电力监控系统数据传输的速率较低，大部分仅1 s/次，数据波动范围不大，监测数据在很长一段时间内围绕某一均值上下波动，最小二乘法可有效跟踪数据波动情况，且在该传输速率下有充足的运算时间；船舶电力监控系统数据传输的测点较多，导致每秒传输的数据量较大，滑动窗口技术可对传输的数据进行分段处理，为后续采用最小二乘法进行数据计算提供便利。基于以上特性，本文根据船舶电力监控系统数据的特点设计一种基于最小二乘法和滑动窗口的数据压缩策略，并在滑动窗口中附加3个数据探测器，实时监测数据和相关参数，以满足监控设备的需要。由于开关量数据不适用于有损压缩方式，故该策略仅适用于模拟量数据。

1 最小二乘法与滑动窗口

1.1 最小二乘法

最小二乘法具有原理简明、收敛速度快、易于理解和易于编程实现等特点，已在系统参数估计领域得到广泛应用。最小二乘法的原理是利用输入数据计算系统参数，使通过系统参数估计的理论值与实际值的差值的平方差最小。从压缩数据的角度分析，记录输入的数据流，给每个数据分配一定的权重，根据权重预测下一个到来的值，使预测值与实际值的差值的平方差最小，该平方差可看作压缩数据的误差。在压缩数据时，只需记录权重分配比和初始值，从而达到减少数据存储量的目的。解压缩之后得到的数值就是根据参数和初始值计算得到的估计值，且估计值与实际值的差值的平方差最小，能在一定程度上保证数据的精度。在船舶电力监控系统中，被控对象会源源不断地提供新的输入数据，可利用新的信息提高数据压缩精度。在船舶运行工况稳定的情况下，数据变化不频繁,在均值附近浮动，可采用递推最小二乘法，加入修正项提高数据压缩精度。递推最小二乘法的表达式为

(1)

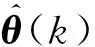
递推最小二乘法的运算步骤如下:

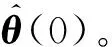
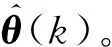
(1) 根据初始数据构造()；

(2) 根据式(1)计算()；

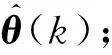
(4) 更新()；

(5)=+1，返回步骤(1)，继续循环。

1.2 滑动窗口

处理数据的窗口可分为固定值窗口、滑动窗口和会话窗口等3种。固定值窗口只处理每个时间段内的数据，不重复处理数据，保证每个数据最多被处理1次；滑动窗口每次处理完窗口中的数据之后，向后滑动，剔除一部分旧的数据，接收一部分新的数据，部分数据会被重复处理，保证每个数据至少被处理1次；会话窗口用于捕捉某一时间段内发生的事件。船舶电力监控系统查询数据以时间为约束条件，因此窗口中的时间序列以数据接收时间为准。根据式(1)，每收到1个数据，即更新1次参数，因此处理数据的窗口采用滑动窗口最为合适。

2 基于最小二乘法的数据压缩策略

本文将测点传输的数据看作数据流，滑动窗口负责控制流入数据的大小，滑动窗口内部的数据先采用最小二乘法压缩处理，再存入数据库中。在采集数据过程中，某些数据受抖动影响，会突然偏大或偏小，这种数据会影响压缩质量，需在压缩过程中将其剔除。若船舶工况发生改变，某些数据会脱离原来的稳定范围，这时若继续采用最小二乘法处理，权重变化较大，数据压缩精度下降，需存储上一阶段压缩的数据并开始新一轮的压缩过程。在压缩过程中，还需监控最小二乘法参数收敛情况，若参数未收敛，则压缩精度较差。综上，在滑动窗口中增加3台探测器，用于提高数据压缩精度。第一台探测器负责监测异常数据，若有异常数据，则及时将其剔除；第二台探测器负责监视数据波动范围，若数据波动范围变化较大，则说明工况发生改变，前一个压缩周期结束，开启下一个压缩周期；第三台探测器负责监视参数收敛情况，若参数收敛，则压缩结果可靠，反之判定压缩结果不可靠。

本文所述数据压缩策略模型见图1，每当有新的数据到来时，处理过程如下：

1) 对新数据进行检测，若该数据不是异常数据，则将其传递到滑动窗口中。在新数据被滑动窗口接收之后，实时更新滑动窗口内部数据的波动范围，若数据波动范围未超过相关阈值，则采用最小二乘法更新压缩参数。

2) 计算压缩参数的收敛情况，判断压缩结果是否可靠。当下一个数据到来时，滑动窗口向前滑动1次，并剔除最旧的数据，重复上述操作，直到满足压缩需求为止。满足压缩需求之后，合并窗口内部的数据，并将其存入数据库中。

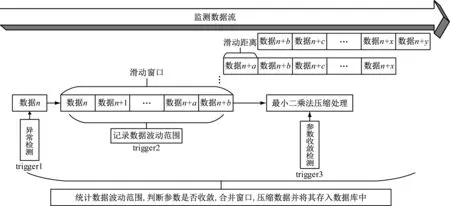
图1 数据压缩策略模型

2.1 异常探测器

异常探测器用于检测异常数据，其结构体定义如下：

struct trigger1{

double lastValue[3];

double nowValue;

double nextValue[3];

double range;

};

当船舶工况稳定时，某一时刻数据前后的几个数据的值相差不大，本文选择前后3个时刻的数据判断数据异常情况。lastValue用于存储该数据之前的3个数据；nextValue用于存储该数据之后的3个数据；range为数据波动范围。计算该数据与这6个数据的差值，若6个差值均大于波动范围，则丢弃该数据，否则将其加入滑动窗口中。

2.2 数据波动范围记录器

数据波动范围记录器用于记录数据波动范围，其结构体定义如下：

struct trigger2{

double arverror;

double standerror;

double rangeup;

double rangedown;

int errnumber;

}

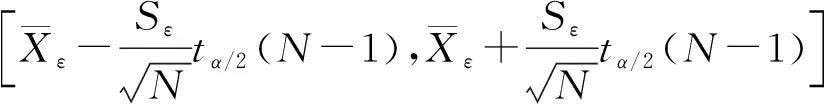
2.3 参数收敛检测器

参数收敛检测器用于检测最小二乘参数的收敛性，其结构体定义如下：

struct trigger3{

double thetaerr;

double futurey;

bool convergence;

double lasttheta[50];

}

lasttheta用于存储前几次计算的参数矩阵；thetaerr为上次计算得到的参数与本次计算得到的参数的残差；futurey为下一个数据的估计值；convergence用于判断参数是否收敛。最小二乘参数需经过一定次数的计算之后才能收敛，只有参数收敛才能保证数据压缩精度。当每次计算的参数的残差小于某一设定值，且估计值与实际值相差不大时，认为参数收敛，数据压缩结果有效。

2.4 压缩数据的滑动窗口

压缩数据的滑动窗口结构体定义如下：

struct window{

int number;

QList〈double〉 data;

int start;

int end;

trigger1 outlier;

trigger2 range;

trigger3 thetajudge;

int errnumber;

};

number为滑动窗口内存储的数据个数；data为数据值；start与end共同确立滑动窗口目前处理的数据所在的位置；trigger1、trigger2和trigger3为附加的3台探测器，用于保证数据压缩精度。

2.5 压缩算法与解压缩算法步骤

1) 压缩算法的步骤如下：

(1) 初始化窗口，初始化相关参数；

(2) 计算接收数据的时间，若超时，则转到步骤(9)，否则进行步骤(3);

(3) 获取新数据，采用异常探测器判断该数据是否为异常数据，若是，则转到步骤(2)，否则进行步骤(4)；

(4) 采用数据波动范围记录器计算数据波动范围；

(5) 采用最小二乘法更新参数；

(6) 采用参数收敛检测器计算参数收敛情况；

图2 压缩算法流程图

(7) 当数据波动未超出指定范围，且参数收敛时，若处理的数据量大于等于100个，则对这些数据进行压缩处理，并转到步骤(9)，否则转到步骤(2)；

(8) 当数据波动超出指定范围时，转到步骤(10)；

(9) 将压缩后的数据存入数据库中，并转到步骤(2)开始新的压缩周期；

(10) 将原始数据直接存入数据库中，并转到步骤(2)开始新的压缩周期。

压缩算法流程图见图2。

2) 解压缩算法的步骤如下：

(1) 判断数据是否为压缩数据，若是，则进行步骤(2)，否则转到步骤(5)；

(2) 读取初始值向量和最小二乘参数；

(3) 根据初始值和最小二乘参数计算解压缩值；

(4) 利用得到的解压缩值还原下一个解压缩值，直到所有数据解压缩完毕；

(5) 直接还原数据。

3 仿真结果分析

为验证本文提出的数据压缩策略的有效性，利用实船采集的真实数据进行压缩测试，通过模拟软件将真实数据发送给网关，由网关传输给服务器。试验环境如下：处理器采用兆芯KaiXianKX-6640A，主频为2.6 GHz，内存为16 GB；操作系统采用中标麒麟V7.0；数据库采用达梦数据库8.0；编译器为Qt5.7。

为衡量压缩效果，引入指标

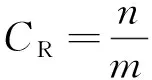
(1)

(2)

式(1)和式(2)：为压缩比；为压缩后数据占用的存储空间；为压缩前数据占用的存储空间，压缩比越小，数据占用的存储空间越小；为压缩数据与原数据的误差百分比；为原数据；为解压缩之后的数据；为数据个数。

下面以应用较为广泛的无损压缩算法(LZ77算法)和工业数据库中常用的旋转门算法为参照，对不同压缩算法的数据压缩效果进行对比，结果见表1，其中LZ77算法采用Qt5.7编译器中的zlib开源库，压缩等级为1。LZ77算法虽然没有压缩误差，但其压缩比较大；旋转门算法虽然压缩比较小，但其误差较大；最小二乘法的船舶电力监控系统数据压缩效果最优。

表1 不同压缩算法的数据压缩效果对比

经不同数据集测试，基于最小二乘法的数据压缩结果见表2。不同数据集的压缩比不同，但压缩误差均在可接受的范围内。基于最小二乘法的数据压缩效果见图3。解压缩数据与原数据相差不大，单个数据误差在可接受的范围内，解压缩数据与原数据的波动趋势基本一致。

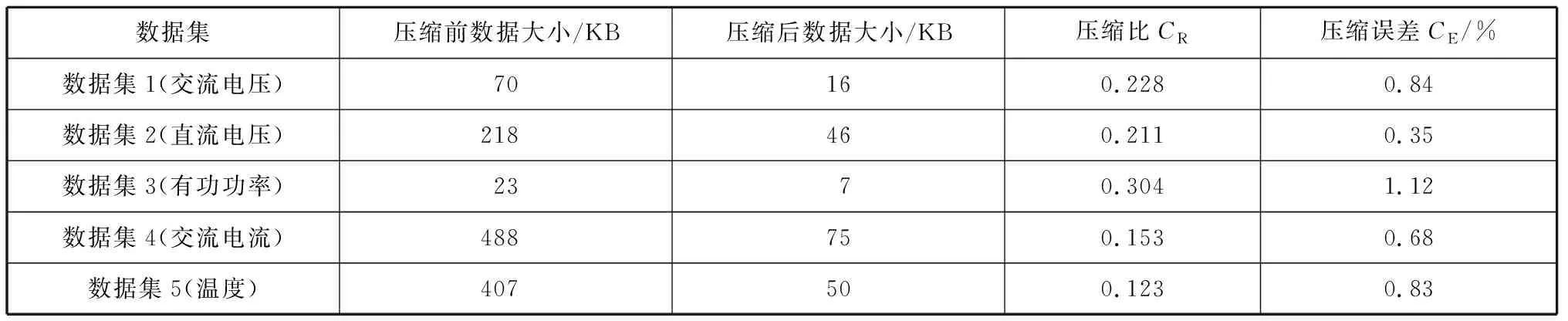
表2 基于最小二乘法的数据压缩结果

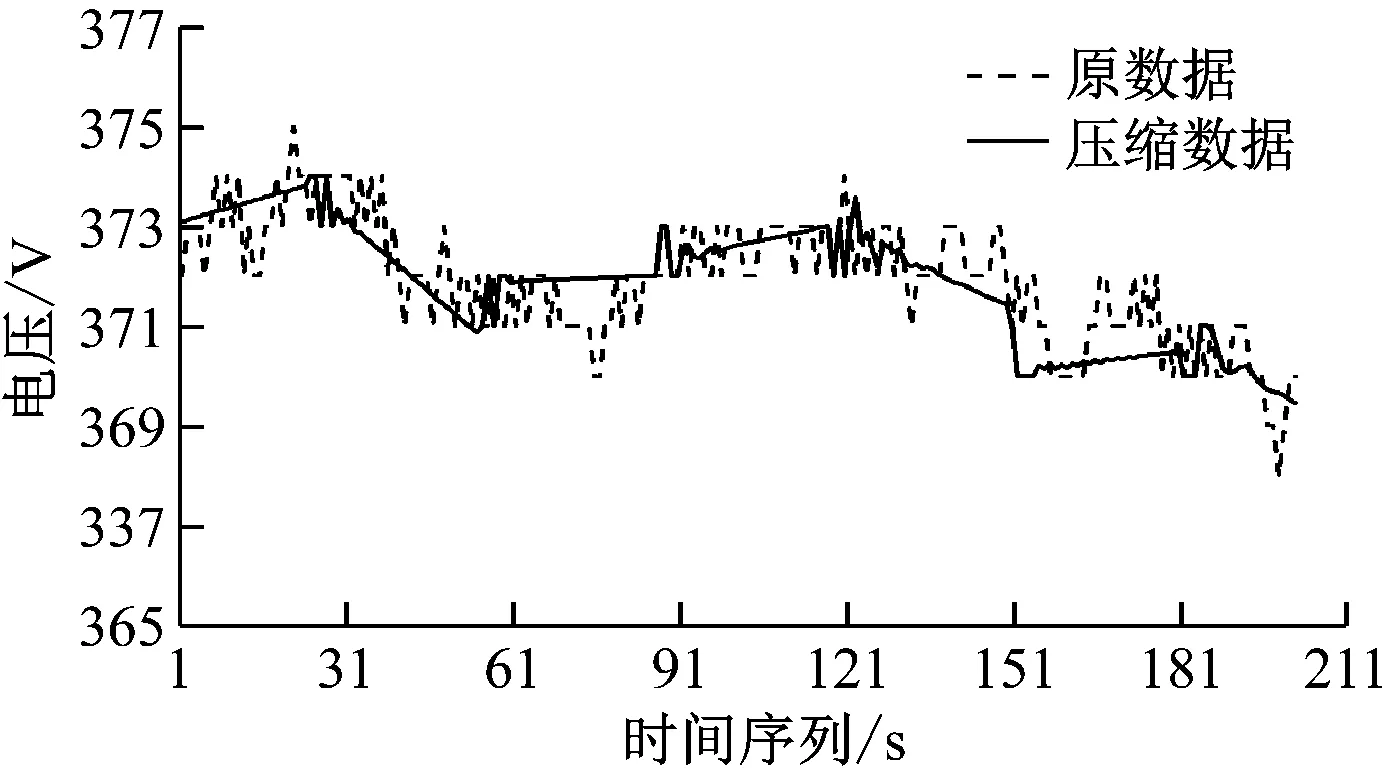
图3 基于最小二乘法的数据压缩效果

综上，本文所述最小二乘法与LZ77算法相比压缩率更低，与旋转门算法相比压缩误差更小。经不同数据集测试，最小二乘法能保持稳定的压缩效果。采用最小二乘法压缩的数据与原数据相差不大，单个数据的误差不会影响数据变动的趋势。本文采用的方法涉及矩阵运算，运算量相对较大。若矩阵维度较高，会造成数据处理不及时，对CPU(Central Processing Unit)的要求更高；若矩阵维度较低，会造成数据压缩效果不理想。因此，需根据实际情况选择矩阵维度。

4 结 语

随着船舶智能化的不断发展，信息的应用变得越来越重要，信息量增加会增大数据存储负荷，数据压缩技术能有效缓解数据存储空间不够的压力。本文针对船舶电力监控系统数据的特点，采用最小二乘法，结合滑动窗口技术设计了一种实时数据压缩策略；同时，利用实船采集的真实数据进行测试，验证了该策略的可行性。试验数据集的大小受试验环境的限制，且无法模拟突发状况下数据的变化情况。本文对阈值的设计较为简单，可能会导致部分数据有较大的误差。下一步将对更大规模的数据进行压缩测试，并将该算法植入监控程序中，测试其在国产化设备上的应用效果。