冰载荷实船测试研究进展

王福花 朱文博 曲 雪 崔海鑫

（1.中国船舶及海洋工程设计研究院 上海200011；2.喷水推进技术重点实验室 上海200011；3.上海交通大学 船舶海洋与建筑工程学院 上海200240；4.上海市船舶工程重点实验室 上海200011）

0 引 言

近年来，随着极地开发的升温，对极地装备的需求日益增加。冰载荷对极地装备设计的合理性以及冰区营运的安全性有至关重要的影响，如何准确预报冰载荷受业界广泛关注。冰载荷实船测试能够提供关于冰载荷的第一手资料，是制定相关规范、理论分析及数值模拟的依据。

本文对自2015年以来的冰载荷实船测试研究进展进行了系统综述，旨在为冰载荷实船测试的应用及进一步发展提供参考。文章首先介绍了当前主要冰载荷实船测试数据内容和方法，然后提出从测试数据换算到冰载荷采用的主要方法，进一步阐述冰载荷的影响因素（如冰厚、航速等）以及冰载荷的空间分布特征，再介绍了基于实船测试数据建立的冰载荷概率模型和设计极值预报方法，最后对冰载荷实船测试研究结论进行了总结。

1 冰载荷实船测试数据内容和方法

冰载荷主要通过实船监测实现。由于冰载荷是极地船舶结构设计中首先需要解决的最关键和基本的问题，因此实际冰况信息的获取和对应的船体冰载荷预报是冰区营运的前提，冰载荷实船监测（Ice Load Monitoring，ILM）长期被用于船体所受冰载荷的统计分析。ILM研究中监测的参数主要包括冰况、船舶位置/运动以及结构响应，这些参数与冰载荷密切相关，可以用于分析载荷特性和其长期概率分布。

冰况主要包括冰区（图1为波罗的海，图2和下页图3分别为北极和南极冰区）、当年冰或多年冰、冰的压缩强度和弯曲强度、冰的厚度、层冰或碎冰，对于碎冰还包括冰的密集度、浮冰块的质量和尺寸等。其中，冰厚是最重要的参数，可用带声波测距系统的电磁电导仪测量，也可用立体照相机或目视观测估计方法获得。根据在波的尼亚湾（Gulf of Bothnia）开展的标定试验，电磁和声波系统测得的含非冻结冰和水的冰脊龙骨厚度可能被系统性低估了60%。

图1 波罗的海结冰频率（结冰频率用百分数表示，100% 意味着每个冬天都结冰）

图2 北极水域最大范围

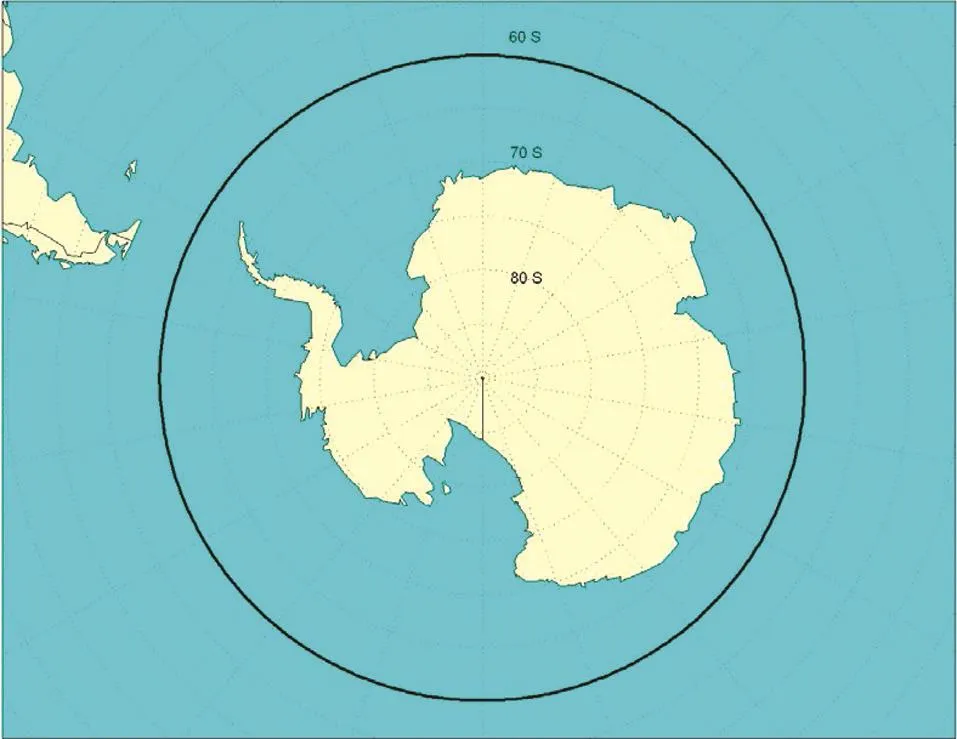
图3 南极水域最大范围

船舶的位置和速度主要通过船上的GPS记录。具有广域增强系统（Wide Area Augmentation System，WAAS）定位的GARMEN GPS可以提供精度为3 m的差分位置，线性加速度和角速度可以通过商业声呐测得，例如Motion PAK II等。由此，可以计算得到船舶的运动和总的外部冰载荷。

结构响应主要为船体板和构件在海冰冲击下的应变/应力、变形或损伤。在冰载荷监测研究中，主要采用应变传感器来监测板和加强筋的应变，从而得到板的正应力和加强筋腹板端部的剪应力。影响系数法是将测得的局部应变/应力转换成局部冲击冰压力或力的最广泛采用的方法，也可以通过测量和收集结构的永久变形/损伤数据来推测极地航行船所经历的最大冰载荷。在1艘复合材料救生艇的冰场实测中，在艏部左舷肩部安装1个六分量测力仪来测量0.1 m厚丙烯酸板上的局部冰载荷，在艏柱檐板上则安装2个载荷单元来测量垂直于艏柱的冰载荷。

基于以上所有关于冰况、船速以及通过应变或损伤转换得到的冰载荷数据，就可以研究冰载荷的长期分布，以及冰载荷与冰况、船舶运行之间的关系。

2 从实船测试数据到冰载荷的换算方法

冰载荷主要通过船体和结构的响应转化而来。在冰的冲击作用下，船体响应主要包括船体运动/加速度、结构的应变/应力和结构变形/损伤等。

2.1 船体应变监测和影响系数法（ICM）

2.1.1 基于外板/骨架应变与外板冰压力关系的影响系数法

冰压力和测得的应变/应力之间的关系可通过有限元模型计算得到。将布有传感器的测量区域划分成特定的单元，分别在每个单元上施加均布载荷，然后计算传感器位置处的应变响应，图4为CCGS号船上传感器布置、图5为单元区域。通过反复计算，可以得到各部位载荷与各监测点响应之间的影响系数，获得影响系数矩阵后，即可将测得的应变/应力转化为冰压力，见式（1）：

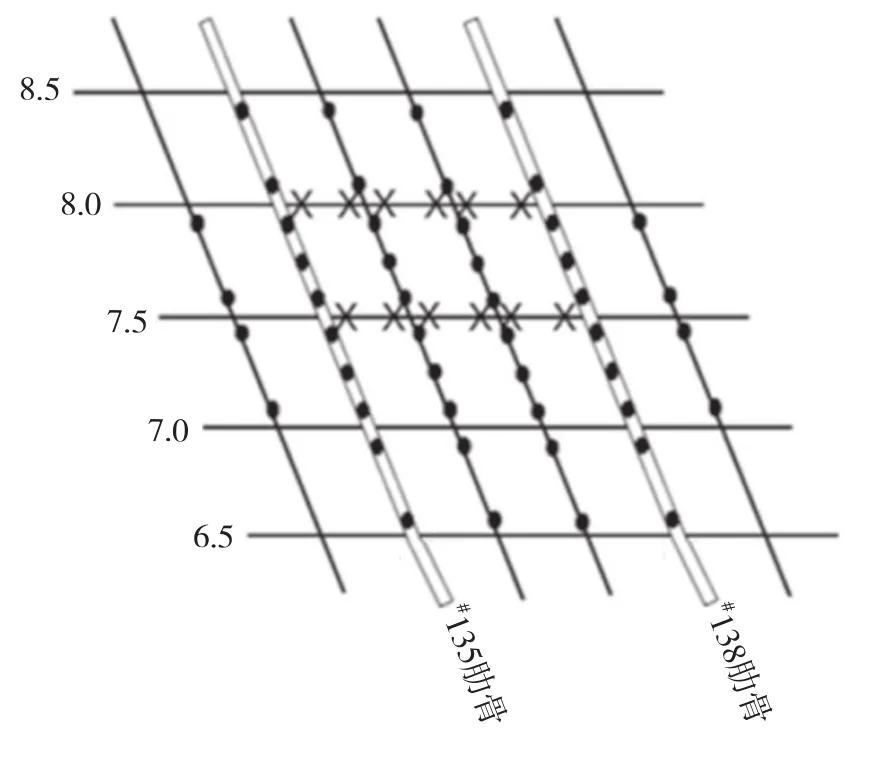
图4 实船应变片布置

图5 假定的载荷单元区域

式中： 、 分别为由每个特定单元组成的应力向量和压力向量； 为压力对应力的影响系数矩阵。

通过实船加载标定试验表明：当在整个单元施加均布载荷时，采用影响系数法预报的载荷比试验值大10%；当仅在单元的一半施加载荷时，影响系数法预报的载荷比试验值平均大19%。

在Araon号于阿蒙森（Amundsen）海的实尺度浮冰碰撞试验中，采用影响系数法和直接法两种方法计算了应变测点L3、L6、L9、R3、R9位置（图6） 的最大冰压力。直接法仅考虑目标区域压力与结构应力之间的关系，而影响系数法同时考虑周边区域压力的影响。影响系数法和直接法得到的压力比ICM/D平均值为1.023 8，范围为0.825~1.133。

图6 Araon号应变片位置

2.1.2 基于肋骨端部剪切应变与肋骨冰载荷关系的影响系数法

另一种可选择的方法是通过分析横向肋骨的剪切应变测量结果来预测局部冰载荷。TAYLOR R S 和 RICHARD M通过实尺度测量发现在当年冰况下，冰压力以线载荷形式作用于船体。基于叠加原理，一个范围较长的载荷可认为是由多个作用于单根肋骨上的子域载荷组成（图7）。冰载荷分力 和其导致的肋骨剪切应变 的关系为影响系数矩阵 ：

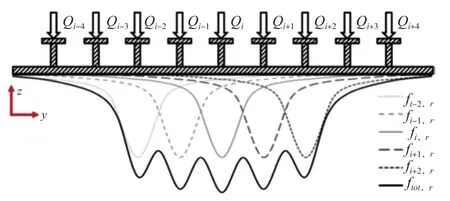
图7 肋骨间载荷分布和相互作用示意图

矩阵 与 互为逆矩阵，矩阵 按式（3）计算得到：

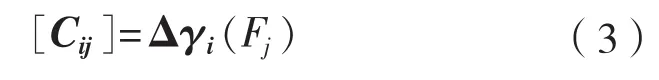
如上所述，通过对结构有限元模型分析可以得到矩阵 ，并用于将测得的横向肋骨剪切应变换算成海冰引起的线载荷。通过S A Agulhas号的实船拉力标定试验，将有限元分析、解析法和试验结果进行了对比，结果显示，解析法得到的总载荷低估了10%，而有限元分析得到的总载荷高估了4%。该标定试验系统的拉力可模拟更大的外载荷，甚至大于10 000 kN。这时相邻肋骨上的载荷值很小，结果吻合良好。

此外，还可直接通过单个肋骨上剪切应变估算其所受的剪切力，该方法与肋骨影响系数法的区别是其不考虑相邻肋骨的影响。图8为肋骨上剪切应变测量和剪力分析示意图。

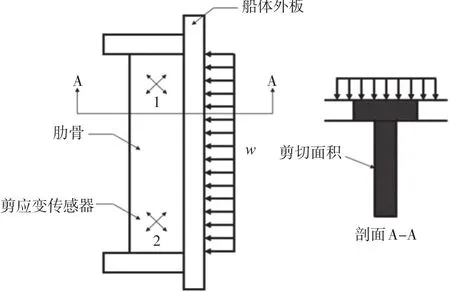
图8 Araon号首部剖面肋骨上应变仪位置

剪切应变是将肋骨腹板端部的十字应变仪测得的数据按照二维摩尔圆方法换算得到的，如式（4）所示。然后按式（5）、（6）可计算得到剪切应力和肋骨上所受的总剪力。

式中：ε、ε、ε分别是图8所示框架上沿水平、45和垂直方向测得的应变；为弹性模量， MPa；为剪切模量， MPa；是泊松比；γ是肋骨剪切应变；和分别是肋骨腹板的上、下端剪切应力，MPa；是剪切面积， mm；是剪切修正因子，由肋骨剖面形状决定，Araon号的值为0.85；为剪切合力，N。

在北极LNG运输船上，肋骨剪切应变用另外一种方法测量，如图9所示。

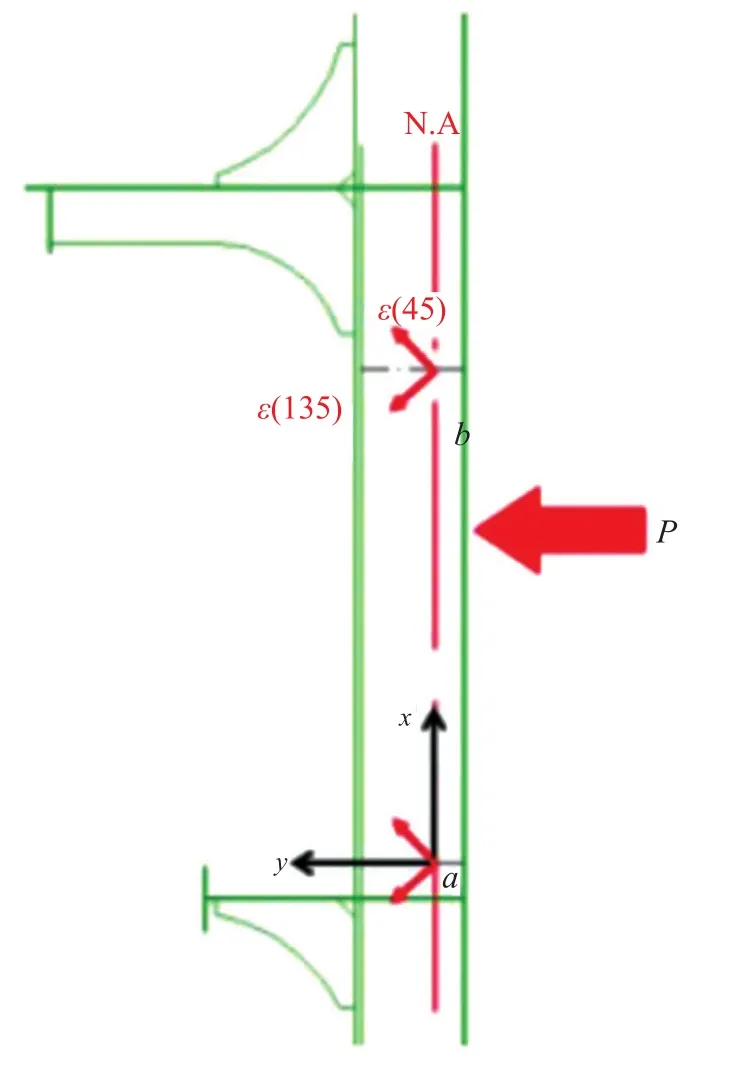
图9 北极LNG运输船肋骨上应变测量位置

其应变传感器位于肋骨腹板中和轴处，轴为平行于腹板方向，应变片分别与轴成45和135。在梁纯弯曲问题中，中和轴轴向应变为0，因此冰载荷可按以下公式计算得到：

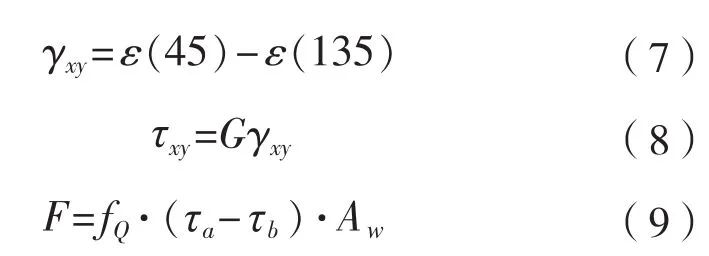
式中：f可通过有限元分析得到，即在目标肋骨处施加单位载荷计算得到τ和τ。以北极LNG运输船的横向肋骨为例，f为1.03。

SUOMINEN M等阐述了冰载荷在肋骨之间可能传递的量值，并且对比了基于肋骨剪切应变的两种肋骨载荷计算方法，即考虑多根肋骨相互作用的影响系数法和不考虑相互影响的单根肋骨直接法。关注MS Kemira号中间剖面承载肋骨，其承担的载荷约为外部载荷的70%，见图10。

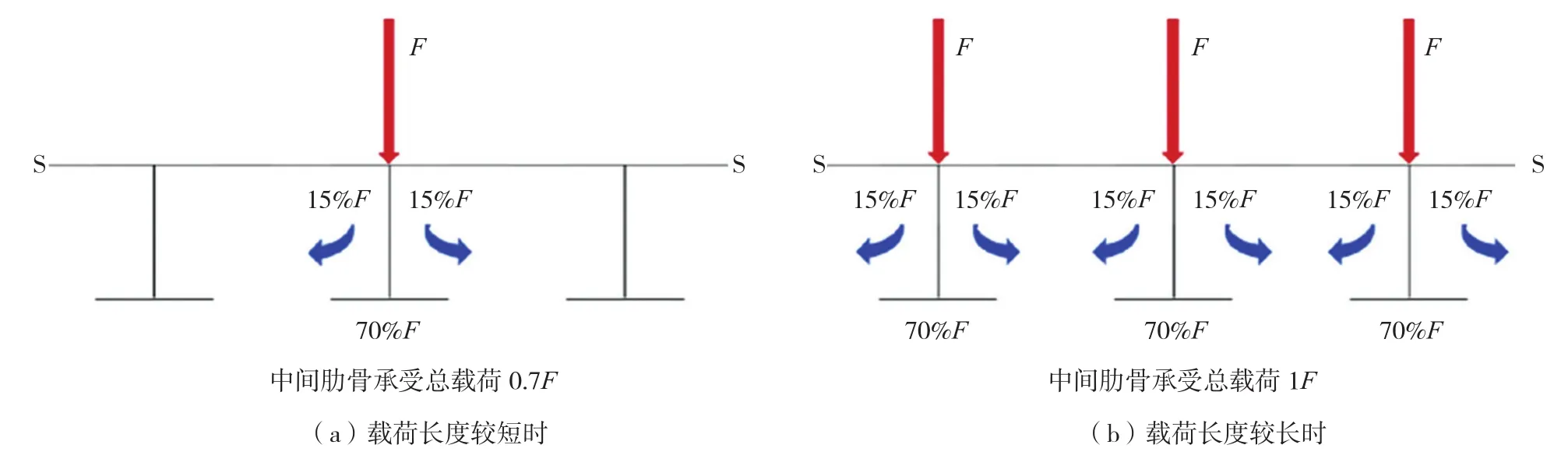
图10 肋骨之间的内部载荷分配（承载肋骨承担外部载荷的70%情况下）

若按照图10（a）单个肋骨上受集中力确定剪切应变与力之间的关系，则当载荷长度达3根肋骨如图10（b）情况下，中间肋骨承受的载荷计算值将达（1/0.7）=1.43，这意味着当载荷长度超过一个肋位时，冰载荷将被高估。反之，当按照图10（b）3根肋骨受集中力确定剪切应变与力之间的关系时，则对于载荷长度比假定工况短时，冰载荷值将被低估。根据S A Agulhas II号船尾肩部实船测试数据，对于载荷长度至少达2个肋骨间距的幅值大于300 kN的载荷事件，采用单根肋骨方法计算得到的载荷值比采用多根肋骨联合影响系数矩阵法高估约15%。

2.1.3 基于外板冰压力与肋骨冰载荷的方法对比

Araon号采用了2种不同的方法来计算局部冰载荷：一种是基于外板应变的影响系数法，即根据外板上应变测量值计算外板所受的冰压力；另一种是基于肋骨剪切应变的直接法，即根据肋骨端部的剪切应变计算肋骨所受的冰载荷。通过2016年共32组的实船测量数据分析，通过影响系数法得到的外板上最大载荷为1.34 MN，略大于作用在肋骨上的最大载荷1.06 MN。总体而言，2种方法得到的局部冰载荷显示了合理的一致性，肋骨上冰载荷峰值平均为船体外板上载荷值的85%左右。

2.2 船体运动监测和MOTAN系统

加拿大国家研究理事会的水动力学中心（NRC-CHC）提出了一种基于船舶运动监测的新型冰载荷分析方法。整个系统称为MOTAN，包括测量装置和冰载荷分析软件GUI程序。该方法假设船为刚体，船体的六自由度运动采用商业传感器Motion Pak II监测，该传感器可测量船的线加速度和角速度。开发的软件系统具有相应算法和分析工具，能够基于船舶运动数据预测船体所受的局部冰载荷，其运动方程见式（10）：

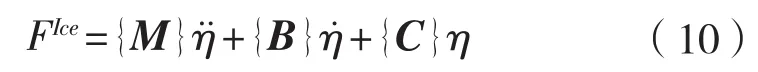
式中：线速度由测得的加速度积分得到；线位移由线速度积分得到；摇摆角加速度和角位移分别由角速度的微分和积分得到。为了消除测得信号中的噪声，采用了0.001~0.6 Hz段的带式滤波器，并且用3次样条插值对测得数据重新取样。 、 和分别是质量矩阵、阻尼矩阵和恢复力矩阵，可根据给定的船体特性得到；水动力附加质量和阻尼系数是在零频率运动假设下，通过三维平板法求得。

通过水动力分析和对海试数据的处理，可计算碰撞点处力的分量，并按式（11）计算总的海冰碰撞力。

在实船破冰试验或航行时，MOTAN系统GUI程序能够基于测得的船体运动参数实现冰载荷的实时计算。MOTAN系统至少已被用于3艘破冰船，包括Araon号和CCGS Terry Fox号等。在CCGS Terry Fox号上同时安装了MOTAN单元和应变仪，以比较冰载荷和碰撞时历等。

Araon号在高纬度北极区冲撞多年浮冰试验中获得了实尺度数据。对于2011年8月11日的1号浮冰试验和次日的2号浮冰试验，利用上述程序预报得到的最大总撞击载荷分别为11 MN和8 MN，与2003年Louis号在加拿大的撞冰试验得到的17.3 MN相比在同一量级。因此，验证了上述总体冰载荷计算方法和程序的合理性及其精度。

LEE S C等根据破冰调查船2015年在楚科奇海和东西伯利亚海域实船冰区试验测试结果，对比了基于运动测量的MOTAN系统和基于应变测量的影响系数法计算的载荷结果。首先根据滤波后低于2 Hz的运动数据得到作用于重心处的六自由度力到，然后根据、和按式（11）可求得重心处合力。另一种方法是根据重心处的六自由度力按式（12）计算撞击部位的总载荷：

结果显示，船体重心处总载荷值比基于应变的计算结果大得多，前者与后者的比值最大达1 907%，见图11。撞击位置处总载荷与应变方法的结果符合更好，比值最大为239%、最小为50%，分别如图11和下页图12所示。

图11 工况28，重心处和撞击位置处合力FCOG、FPOI与应变方法结果S/G相比

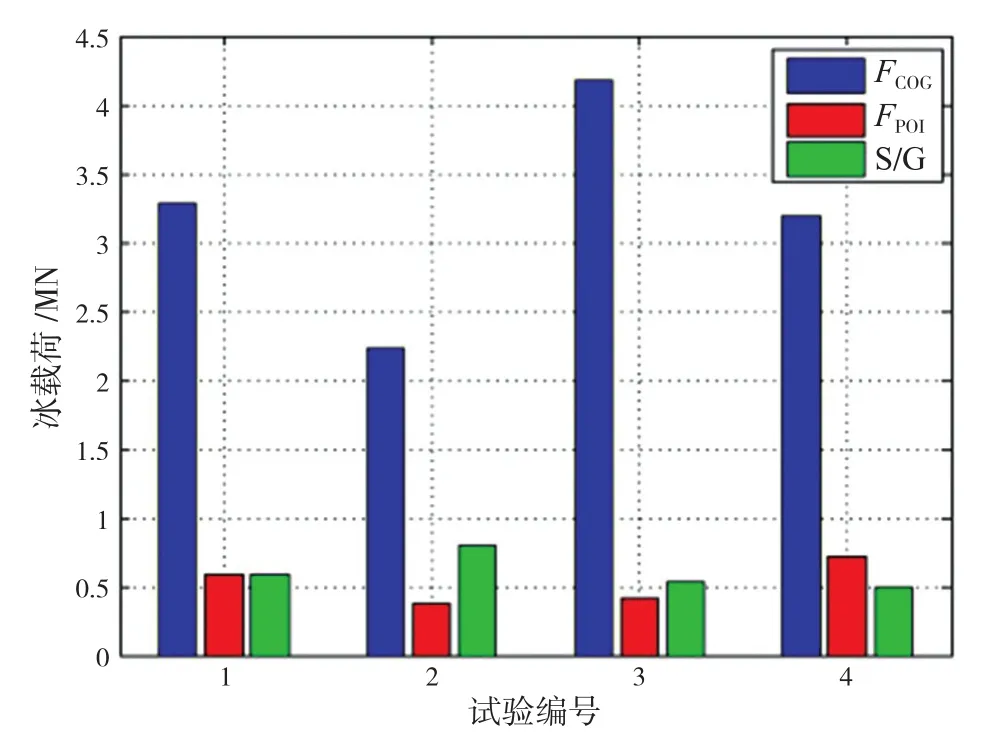
图12 工况5，重心处和撞击位置处合力FCOG、FPOI与应变方法结果S/G相比

2.3 基于船体损伤的载荷水平分析

此处的损伤是指冰区加强船舶外板的小量永久凹陷。首先要收集船舶损伤数据库，对受损的结构要有足够详细的描述。KUJALA P给出的数据库是一个很好的样本，该数据库包含了1984年至1987年冬季定期航行于波罗的海共61艘船的损伤数据，通过这些损伤数据，可以估算船舶遭受的极端载荷。另一种是HAYWARD方法，他建立了回归公式用于确定板在均布局部载荷下的屈服线理论。

引起纵骨架式板变形的线载荷的上限可按下式计算：

当w/≤1时：

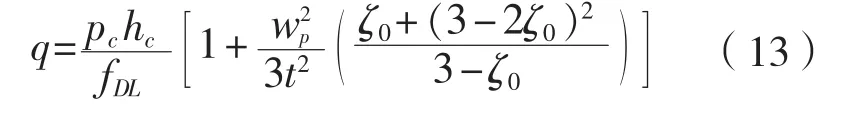
当w /> 1时：

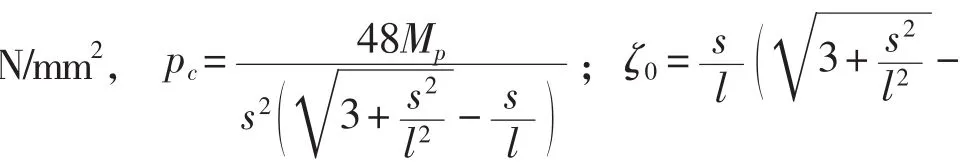
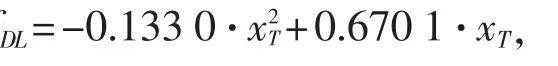
以上两式中：为骨材间距， mm；为骨材跨距，mm；σ为外板的材料屈服强度， MPa。

第二种方法是非线性有限元模拟。该方法的思想就是计算在各种载荷布置（冰载荷的高度和长度）下的结构响应，然后卸载，再找出引起的变形与实船测得的损伤正好匹配的载荷布置形式。KUJALA P等用有限元模拟分析了一个损伤案例，并与HAYWARD公式的结果以及之前损伤分析进行对比，得到了关于波罗的海冰况下可能遭受最大载荷水平的清晰图表，如图13所示。在MS Kemira号的中部/尾部某肋骨上测得的最大载荷1 140 kN/m与图13中基于损伤数据的载荷水平有较好的一致性。

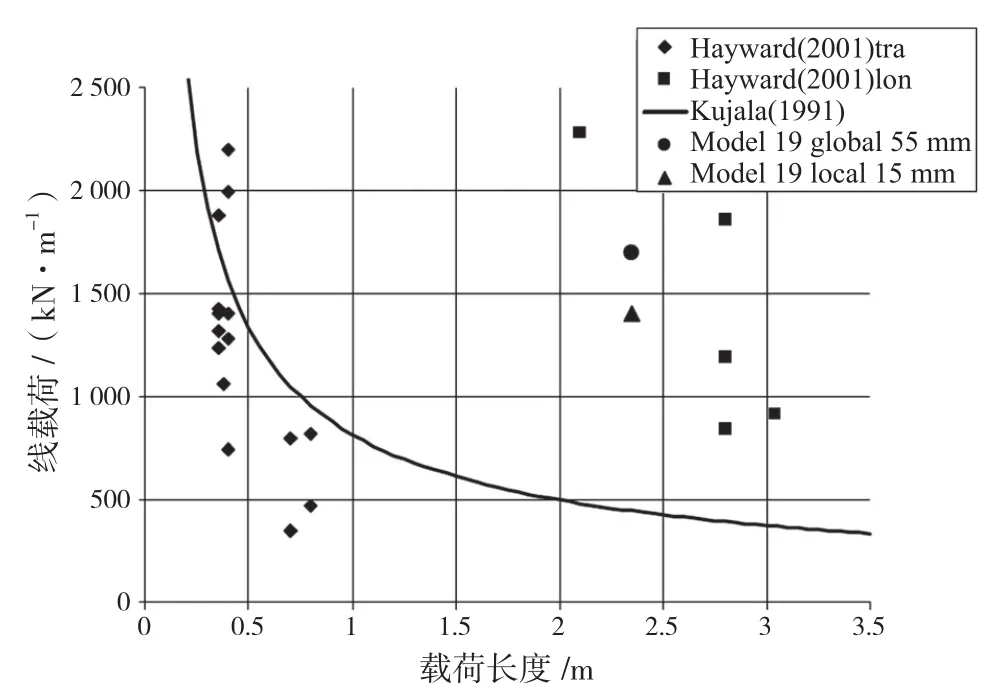
图13 板的损伤结果对比：Hayward（2001）公式、Kujala（1991）曲线和有限元分析结果（Valkonen，2006）

3 冰载荷的影响因素和空间分布特征

冰载荷可能是局部压力、局部线载荷（力/长度，主要沿水线）、某个肋骨或特定区域上局部力以及整个船冰接触区域的局部合力或由其引起的船体梁上总载荷。我们主要关心的是船体不同区域不同结构构件上冰载荷的大小和分布，以及载荷和冰况、船舶参数或作业等之间的关系，从而预测载荷对包括不同结构的应力、变形、振动和损伤等响应的影响。

3.1 冰载荷的影响因素

冰载荷和冰况、船舶作业，特别是和冰厚、船速的关系已被广泛研究。

RITCH R等分析了2001年6月期间CCGS Terry Fox号船与当年冰组成的冰块碰撞试验测得的冰载荷，并将其与1991年Oden号、1994年Louis S.St.Laurent（LSSL）号在北极航行期间撞击多年冰得到的压力-面积概率分布曲线进行了对比。结果显示，Oden号和LSSL号获得的极地多年冰压力包络线要高于当年冰。与不同质量冰块碰撞过程中最大峰值压力和总载荷的超越概率的对比显示，质量对局部压力存在较大影响，而船舶速度无明显影响。当冰块的质量为0.01~0.033、0.1~0.25和1.21（为船舶总质量，约7 000 t）时，对应的0.33 m面积上、10超越概率的压力分别为0.25、0.5和（≈ 5 MPa）。

LEIRA B等主要关注巡逻艇KV Svalbard号在2007和2008年冬季于巴伦支海和斯瓦尔巴群岛附近航行时船体受到的冰载荷。每根肋骨上的冰载荷均基于自身剪切应变独立计算得到其剪力，并研究了冰厚和船速对应变水平的影响。考察冰载荷随冰厚的时历变化，冰厚的突然增加引起了单根肋骨上高载荷峰值的出现。考察冰载荷平均值与船速的时历变化，发现了明显的正相关性；但是，载荷峰值上升过程中却伴随着速度的下降，这可能是由于船舶遭受的冰层阻力增加，因此导致速度的降低和相应载荷峰值的升高。考察船速与冰厚的时历变化进一步支持了这一点。观察发现：冰厚峰值出现的时间段，会出现典型的平均速度下降，相比平均速度，瞬时速度下降更加明显。

RAHMAN M D等分析了一艘玻璃钢救生艇于2013、2014年冬季期间在淡水湖实船试验中测得的冰载荷。浮冰块是从层冰中切取的，平均尺寸约3 m×3 m，2014年冰块厚约0.51 m，质量约4 590 kg，相当于TEMPSC满载排水量的1.25倍左右。但2013年冰厚略薄，单块冰的质量大致与TEMPSC满载排水量相等。对应高、中、低的冰密集度（C = 0.8~ 0.9，C= 0.6 ~ 0.7，C= 0.5）将冰载荷数据被分为3个等级。2013年在船首和肩部测得的最大载荷分别为63.6 kN和34.4 kN；2014年分别为117.9 kN和62.7 kN；然后通过测得的载荷得到了给定区域的峰值压力。结果显示：

（1）船体首柱的局部压力比船首肩部大很多；

（2）高密集度可能导致单位距离更高的碰撞次数，从而导致更高的局部压力，但并不总是这种情况，同样也取决于冰密集度的局部变化和船冰碰撞方式（见图14）；

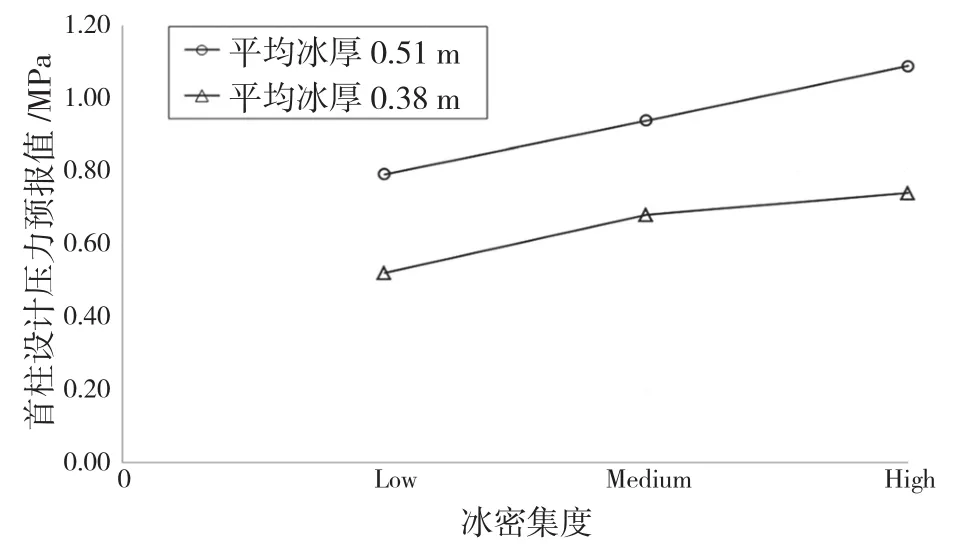
图14 两种冰厚/质量下艏柱设计压力预报值的对比

（3）2014年测得的压力明显高于2013年，主要是由于2014年冰块的平均质量是2013年的1.25倍（见图14）。

除了上述试验，为了测量极值载荷，还开展了8组给定轴转速下的首柱与浮冰的直线撞击试验。结果分析显示冰载荷与碰撞速度存在正相关性，对于大的冰块（冰块质量约为1.25倍的TEMPSC排水量），相关系数约为 0.88（见图15）。

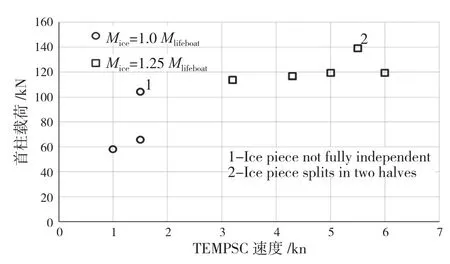
图15 单块冰撞击试验中艏柱载荷与船速的关系

KOTILAINEN M 等分 析 S A Agulhas II号2012年3月波罗的海航行中一根肋骨上的冰载荷。结果显示，载荷水平总体上随冰厚增加而增加，而船速的影响却是双重的（图16）。在低速时（<5 m/s），载荷随速度增加而增加，但在更高速度下（≥5 m/s），载荷幅值一般随速度增加而减小，而最大载荷随船速增加继续增加（见图16，50 cm冰厚）。

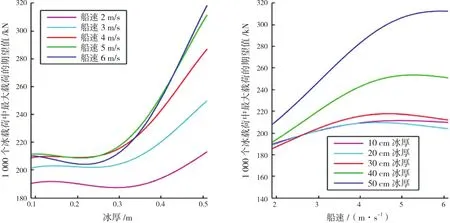
图16 不同工况下1 000个载荷中最大值的期望值

JEON M等分析了Araon号在2015、2016年北极航行时艏部板架测得的应变。基于2016年的实船测试数据，冰载荷峰值在特定速度区间（3~7 m/s）明显聚集，船体外板和骨架上的最大冰载荷都发生于船速为4.52 m/s时（见图17）。为了验证这个趋势，又分析了2015年的实船测试数据，冰载荷峰值同样聚集在在船速3~7 m/s范围内，最大值发生在4.64 m/s。

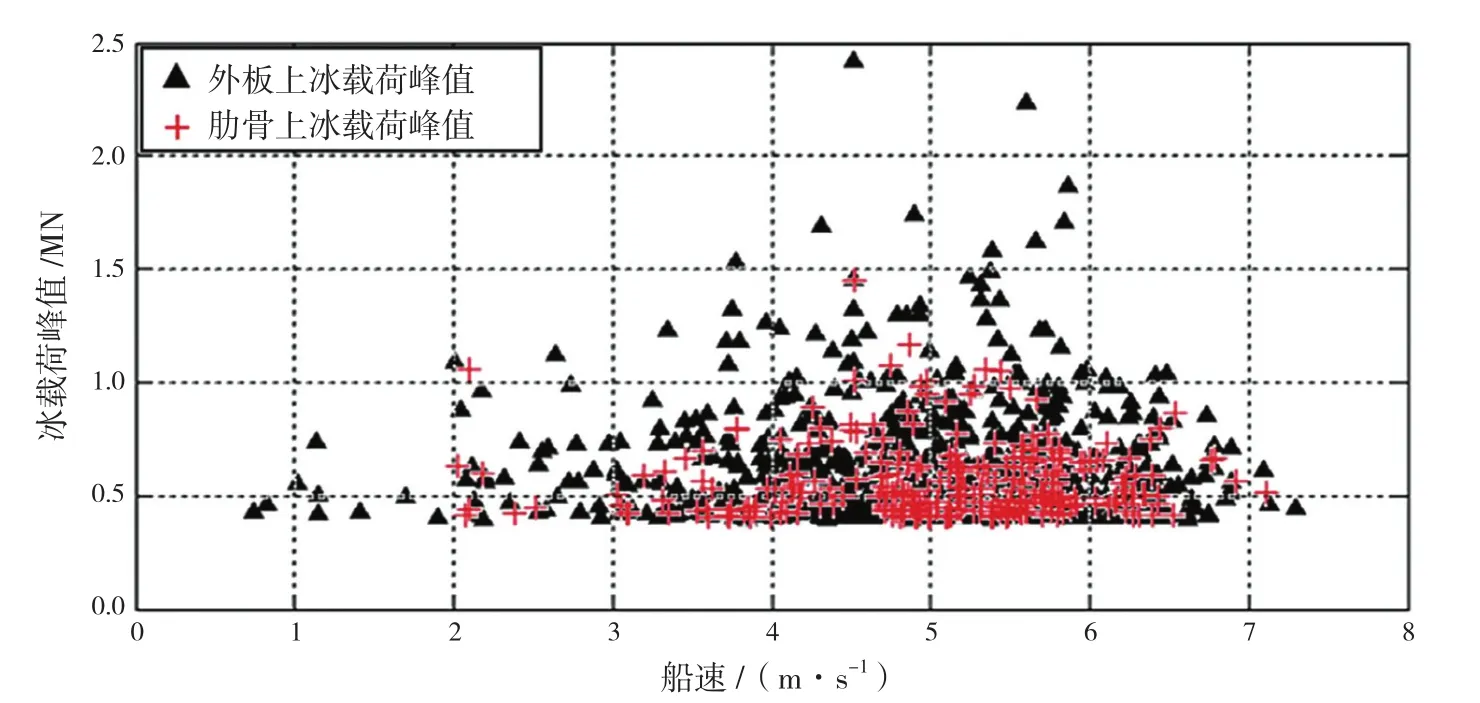
图17 船体外板和肋骨上冰载荷峰值VS船速

KWON Y H等研究了2012年1月31日到3月30日在南极Amundsen海2次破冰试验的船首左右两侧板架上测得的冰载荷。第1块浮冰约900 m×600 m，第2块浮冰约1 100 m×600 m，两块冰经评估均为当年冰。第1次试验分3段航程，分别采用了8 MW、6 MW和5 MW的主机功率；第2次试验的主机输出功率为7 MW和8 MW。

在这2次南极破冰试验的数据中，20.0 MPa及以上的峰值应力被筛选出来，得到峰值应力随速度的变化如图18所示。最大峰值应力（180.7 MPa）发生在第2次试验左舷板架，对应速度约3.42 kn。关于最大载荷没有在最大速度测得的特定趋势，很可能是由于在恒定主机功率时，仅在较薄的冰厚中才能达到较高速度，较薄的冰厚也导致冰载荷较小。

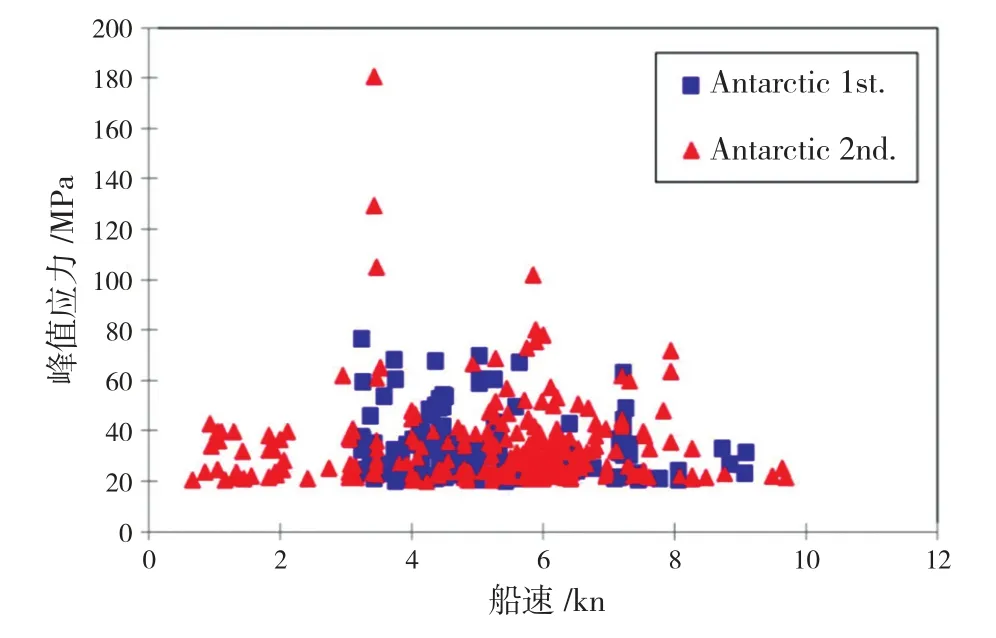
图18 在Amundsen海试验中，结构峰值应力随船速的变化

3.2 冰载荷的空间分布

RITCH R等研究了CCGS Terry Fox号碎冰碰撞试验中的压力-面积关系曲线。将178次船-冰碰撞中的船首肩部外板和骨架上的应变数据通过影响系数法（ICM）转化得到冰压力。任何单个事件的压力-面积关系按下述方法建立。对于每个事件的每个时间步：

（1）选取最大单元压力对应的单元，将这个点绘制在压力-面积图中。

（2）选取与第1个单元相邻的次最大压力单元，即与第1个单元在一条边或者一个角上接触，将这个点绘制在压力-面积图中。

（3）重复上述过程获取第3单元组、第4单元组等。将每个点绘制在压力-面积图中。

按此绘出单个单元最大压力时刻的最大压力-面积曲线，所有最大压力时刻下所有事件的最大压力-面积包络线拟合得到一条线：= 3.5（见图19）。同样得到 1991 年 Oden 号和 1994 年LSSL号在北极多年冰航行时类似的曲线：= 6。

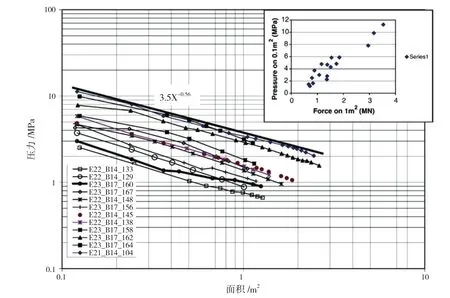
图19 单个单元平均压力最大时刻，对应最小单元的最大平均压力-面积曲线

结果显示，通常最小面积的压力越大，则整个碰撞区域的整体压力-面积曲线越高，即导致更高的合力或给定面上的压力。这种情况通常是正确的，因为加载试验显示了相似的峰值压力分布。每个事件都有中心高压力区，并且随着远离峰值位置，压力逐渐减小。

SUOMINEN M分析了 S A Agulhas II号的船尾肩部4个肋骨上的冰载荷数据，载荷值通过影响系数法（ICM）由肋骨剪切应变转化得到，该试验是2012年3月21至22日在波罗的海当年冰中进行的。载荷事件是采用Rayleigh分离法从时历数据中识别出来的，分离系数= 1/2，阈值为10 kN/m。基于测量结果，实际载荷长度根据同一时刻所受载荷超过阈值的相邻骨架数量确定。研究显示，载荷长度短的情况比载荷长度长的情况更加常见，并且单根肋骨上的最大载荷随着载荷长度增加而增加。这意味着载荷需要足够宽，才能使单根肋骨上出现最大载荷（见图20），这和之前关于局部和整体压力的研究一致。

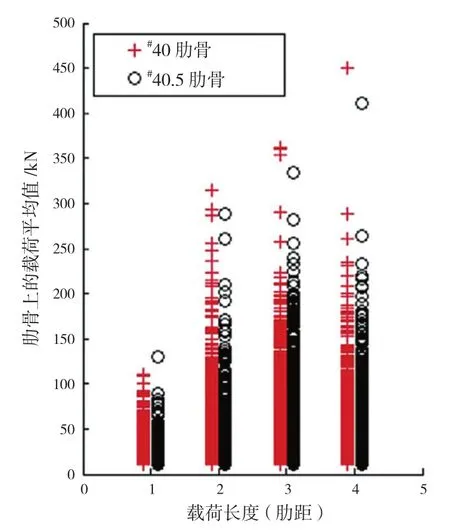
图20 不同真实载荷长度下#40和#40.5肋骨上载荷

有意思的是，载荷长度超过两倍肋骨间距后，其整个长度范围内肋骨平均载荷的最大值不再增加（见图21），而肋骨平均载荷随选取的载荷长度减小（见图22）。

这里真正的区别是，图21中的载荷长度是真实载荷长度，图22中的载荷长度所考虑的则可以是真实载荷长度的部分或全部。如载荷长度为4个肋骨间距时，在图21中只会出现在横坐标4位置处，而在图22中则会同时出现在横坐标1、2、3、4处，纵坐标表示该工况在40、40.5肋骨处的局部线载荷大小。

图21 不同真实载荷长度下肋骨上的平均载荷

图22 空间线载荷随载荷长度的变化。图例中的肋位号表示该载荷工况根据瑞利分离系数识别

KWON Y H等分析了Araon号在南极Amundsen海两次破冰试验中船首左、右两舷外板测得的冰载荷。结果显示，当左舷外板上测得较高水平的峰值应力时，右舷的应力非常低，反之亦然。同一时刻两边应力比值的平均低于7%，几乎不会出现两边同时测得较大应力的情况。显然这意味着，在破冰试验中，两舷同时与冰相碰的情况不会出现，且被认为是反常的。

4 冰载荷概率模型和设计极值预报

冰是一种特殊的非均匀材料，因此船体破冰过程中载荷很难准确预报。冰载荷同样具有很强的随机性和概率性，因此诸多学者致力于建立一个冰载荷（压力、线载荷等）的概率模型，用于预报船舶设计载荷极值，较为有效的方法是依据实船测试数据建立冰载荷与冰况、船舶作业参数之间的联系，寻求最适合的分布函数。

4.1 局部冰压力概率模型

RAHMAN M S等通过 Tempsc号救生艇冰湖碎冰航行试验。基于最大事件方法测得的冰载荷和压力按低、中、高密集度进行分类，每一类分别用Weibull分布对艉部（峰值压力中20%大值）进行拟合，假设艉部满足指数分布得到最佳拟合线。然后，将每个类别中峰值压力20%大值进行组合，从而针对艏柱和艏肩部分别建立压力概率分布，如图23至图26所示。

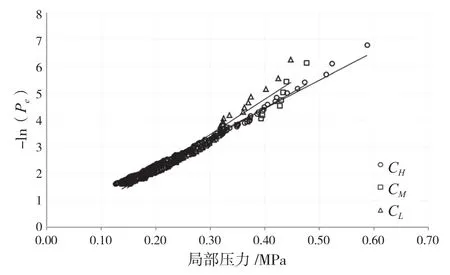
图23 艏柱撞冰局部压力曲线（2014）

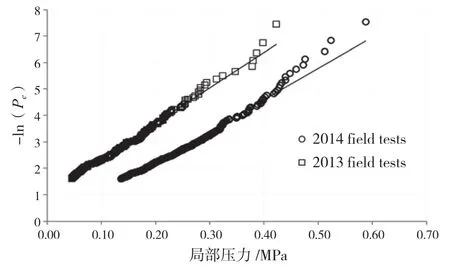
图24 艏柱撞冰局部压力对比（2013，2014）

图25 艏肩部撞冰局部压力曲线

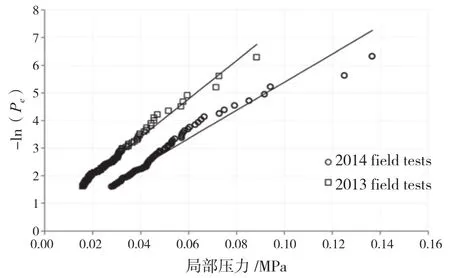
图26 艏肩部撞冰局部压力曲线对比（2013，2014）

基于2013和2014年数据系列，计算得到10超越概率、1 km航程对应的首柱设计压力极值（见图14），结果比海试（包括直线碰撞试验）测得的最大值更高，由此说明提出的设计方法为该研究工况范围提供了保守的设计压力预报结果。同时，也得到另一个结论：如果能够得到足以代表救生艇设计寿命内遭遇的冰况下的实船现场测试数据，最大事件方法为建立救生艇基于风险的设计衡准提供了一种有效的途径。

4.2 压力-面积曲线和概率模型

RITCH R等基于概率分析研究了特定面积上的设计压力极值。CCGS Terry Fox号在纽芬兰东北岸的178次船-冰碰撞数据被分成不同的规定“设计面积”组，基于不同面积的平均压力数据系列，可计算对应面积下的平均压力超越概率（见下页图27），设定超越概率为10和10，可得到平均压力设计值与面积的函数关系如式（17）和式（18）所示，它显示更低的超越概率具有更强的面积效应（见下页图28）。

图27 不同“设计”面积上的平均压力超越概率

图28 基于CCGS Terry Fox号船冰相撞数据，不同概率水平下的平均压力-设计面积关系

RITCH R等同时也指出压力-面积关系（-曲线）代表了其趋势特征，在更详尽的分析之前还不宜直接用于设计中。

CHO S等基于Araon号2016年北极海上试验数据，采用上述方法分析了-关系。对每个面积冰压力尾部分布可以式（17）、（18）所示指数形式拟合：

式中：为随机变量，代表冰压力（MPa），如图29所示；P为超越概率；接近0或为负值，因此可忽略；对一个特定的面积（m）来说为常量。

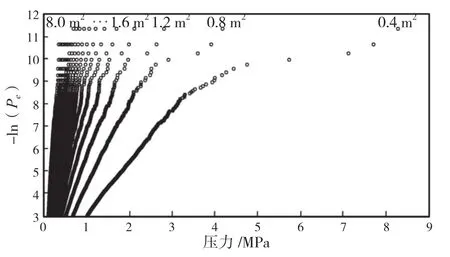
图29 根据不同的面积分级的Araon号实测局部压力数据

基于式（17）和（18），考虑结构面积的遭遇概率和Araon号船冰碰撞次数（每小时约5.5次，以每年1 000 h航行计，约5 523次），对应1年内超越概率为1%的局部压力预报公式如式（19）所示：

式中：为接触面积，m；为与面积对应的平均压力，MPa。

为了考虑除接触面积以外更多的冰-结构影响因素，画出压力-速度、压力-冰厚的无因次对数坐标关系如图30和图31所示，基于图中数据分布的上极限直线给出如下公式：

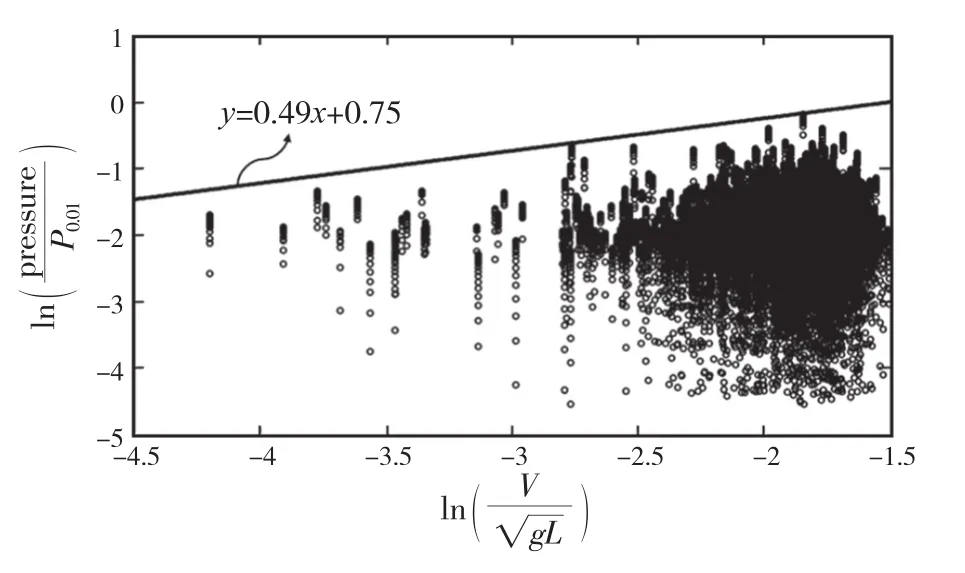
图30 浮冰碰撞压力和船速的关系

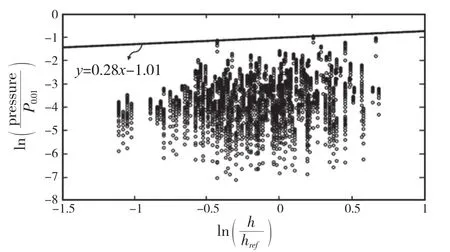
图31 浮冰碰撞压力和冰厚的关系

对于Araon号，包括船速和冰厚等设计因素的修正后的-关系式如下式：

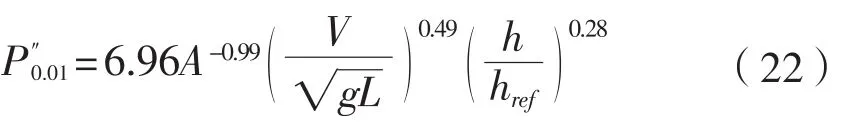
4.3 基于冰厚和外飘角的冰载荷半经验概率模型

MS Kemira号、MS Arcturus号和MT Kshira号均装有测量仪器，并分别在1985年至1992年、1983年至 1988年和1984年至1990年冬季开展实船测试。KUJALA P等以MS Kemira号的长期测量数据为基础数据库，采用一种半经验方法建立了可用于波罗的海长期冰载荷预报的概率模型，并以该方法对MS Arcturus号和MT Kshira号进行载荷长期预报，并与实船长期测量数据进行对比验证，整个分析过程中均以船首某根肋骨上的载荷为研究对象。

首先将波罗的海分为4个区域（参见图1），然后通过冰载荷仿真得到基于平均值和冰脊百分比的冰厚等效因子。将每个冬季MS Kemira号艏部肋骨上所测得的12 h最大冰载荷值按照上述海域归类，并与对应海域的等效冰厚关联。载荷平均值和变异系数如图32、图33所示，图32中的平均值根据最大破冰能力（对于MS Kemira号为0.5 m）分为两个部分。

图32 艏部肋骨实测12 h最大冰载荷平均值与等效冰厚的关系

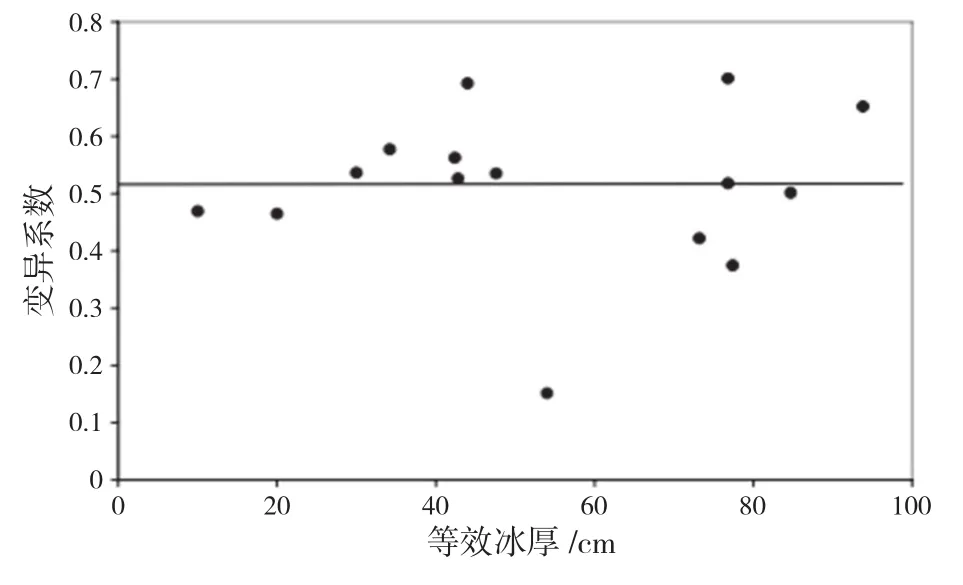
图33 艏部肋骨实测12 h最大冰载荷变异系数与等效冰厚的关系

一旦确定了平均值和变化系数，就可用Gumbel 1型极值分布描述冰载荷的统计特征，计算得到Gumbel参数c、u，则每个海域的长期累积概率分布函数为：

全寿命期的最终冰载荷累积分布函数为：

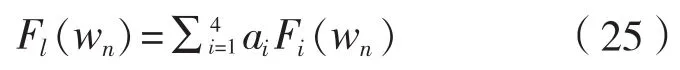
冰载荷重现周期（天）：

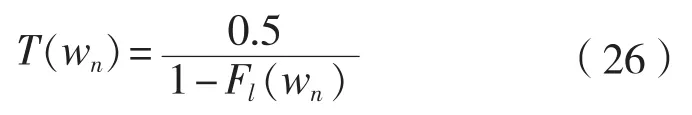
式中：w为12 h最大冰载荷，N；h为最大等效冰厚，m；u和c是Gumbel系数，与测得的平均值m和变化系数δ相关。

利用上述公式，可得到线载荷（冰载荷/骨材间距）的累积分布（如下页图34）。对于其他船，图32中的斜率可以用最大破冰能力和肋骨外飘角β换算得到：

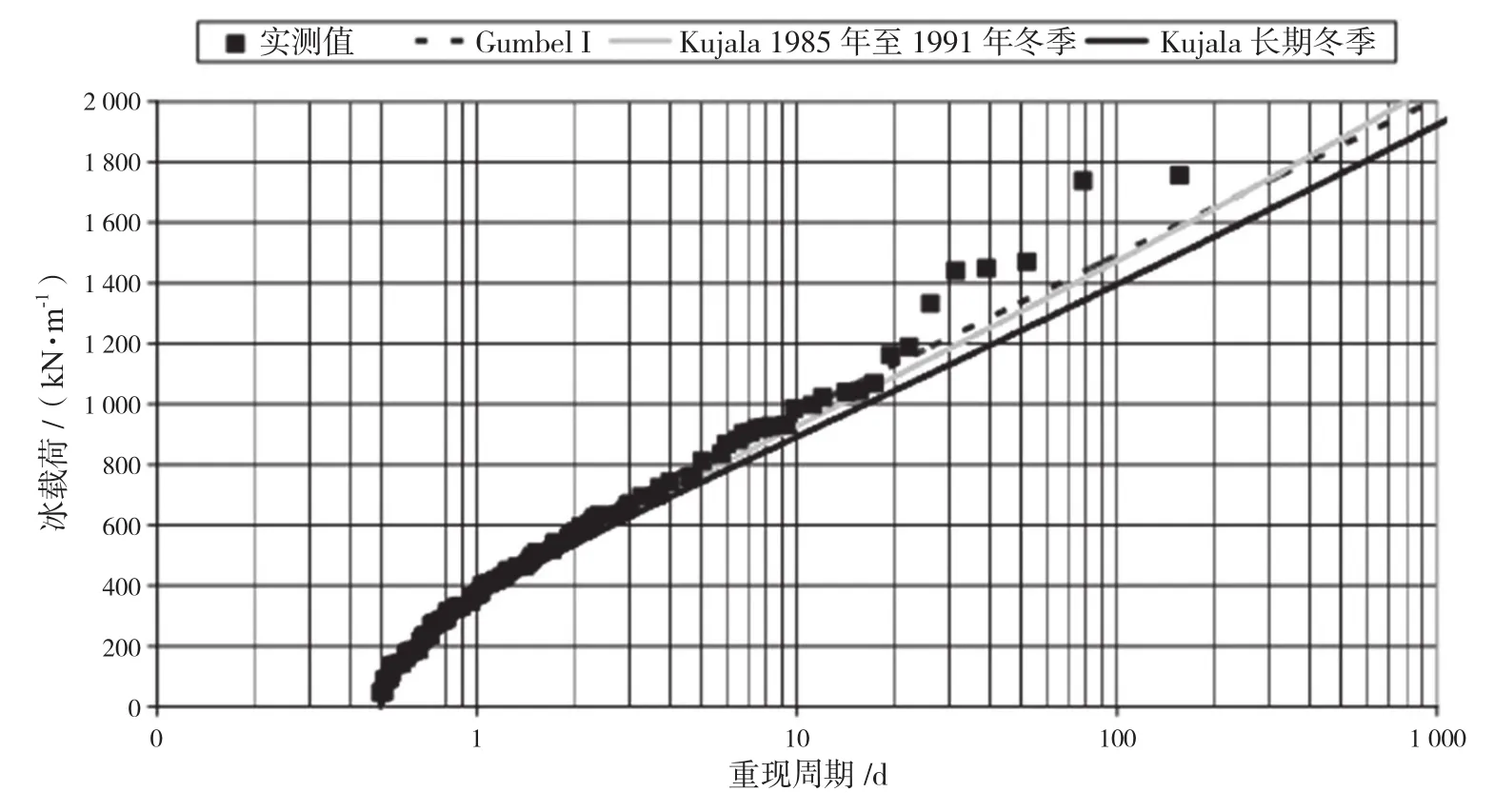
图34 MS Kemira号艏部肋骨冰载荷长期分布与实测值的对比

式中：带下标的为新的目标船参数；系数可通过船冰碰撞过程中海冰边缘失效模式分析得到，=1.46。

基于上述方法得到MS Arcturus号和MT Kashira号的线载荷概率分布，并与直接通过测量数据拟合得到的Gumbel 1型曲线进行对比（下页图35为MS Arcturus号），对比结果显示，该半经验方法与实测最大值吻合良好。

图35 MS Arcturus号艏部肋骨冰载荷长期分布与实测值的对比

KUJALA P等又基于上述方法对S A Agulhas II号船的长期分布载荷进行了预报，其数据来源于该船在2012年至2018年冬季共7年期间，在南极航行实测得到的层冰厚度和艏部2根肋骨的冰载荷（134+400，134）。具体冰厚下的平均冰载荷和相应的变异系数如下页图36和图37所示，推导得到艏部两根肋骨的冰载荷如下页图38和图39 所示。

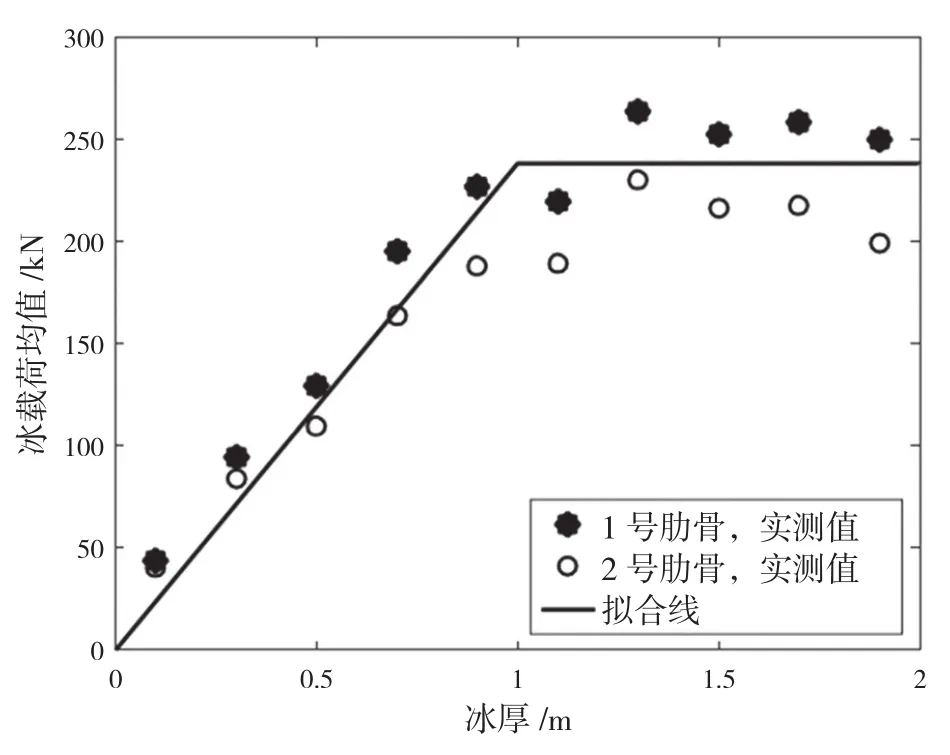
图36 平均冰载荷与等效冰厚的关系

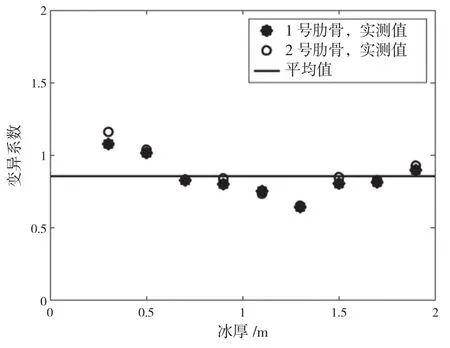
图37 冰载荷变异系数与等效冰厚的关系

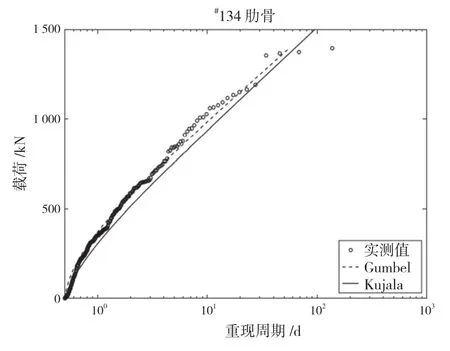
图38 #134肋骨预报和实测的载荷极值重现期

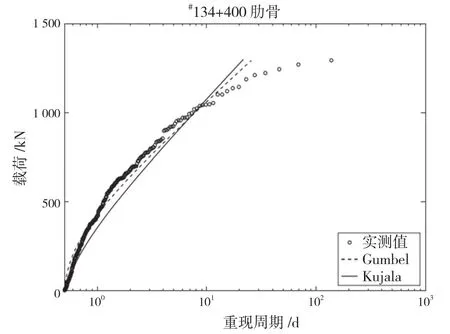
图39 #134+400肋骨冰载荷变异系数与等效冰厚的关系

4.4 基于冰厚和船速的冰载荷高斯过程模型

2012年3 月S A Agulhas II号在波罗的海航行并开展了为期2天的冰场试验，冰载荷通过应变仪测量得到。船首134.5号肋骨上的冰载荷通过骨材端部的剪切应变转换而来，并采用Rayleigh分离系数法识别获得，将冰载荷与同一时刻的冰厚、船速作为基础数据。为了更好地处理分析那些因破冰导致的异常小的冰厚数据（即实际相机拍摄时冰已经破裂情况），对冰厚的对数采用了Student-t观察模型。使用了4个层次的高斯过程（GP）模型描述冰载荷在冰厚和船速协变量空间内的短期分布（下页图40）。在所有测试模型中，变尺度和形状参数的Weibull 模型表现最好，重复样本数据中最大的载荷与测得冰载荷最大值378 MN相近，变尺度参数Weibull模型次之，前者预报的最大值载荷极值概率接近后者的3倍。对于指数模型和对数高斯模型，预报的最大载荷总是一致偏高或一致偏小。

图40 4个关于协变量的载荷分布高斯过程模型的总结

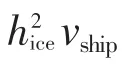
图41 冰载荷极值随 的散布图

4.5 冰载荷极值预报平均条件超越率方法

为了建立冰载荷短期极值分布提出了2种不同的方法，即峰值方法和时间窗口方法。峰值方法引入统计模型来描述测得的冰载荷峰值母体（初始）分布，时间窗口方法将测得的时间序列分割成一系列相等的时间窗口，并识别出每个时间窗口的最大值，基于上述最大值数据，用次序统计获得其经验累积分布。CHAI W等介绍了用于极值预报的经典峰值方法，以及基于分时段最大值和Gumbel分布的渐进方法，然后提出了一种新的平均条件超越率（Average Conditional ExceedanceRate，ACER）方法作为冰载荷长期预报方法。

式中：， …，X表示记录的冰载荷峰值。

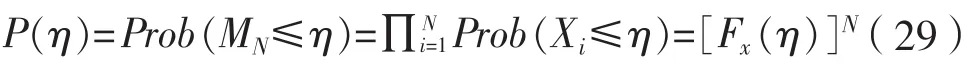
对于一个小量的超越概率水平，相应的极值概率为：

然而存在一个限制峰值方法应用的关键点，即测得的载荷峰值平稳性，而这只能在一些理想工况得到满足。

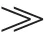
式中： 是Gumbel分布，具有如下表达式：

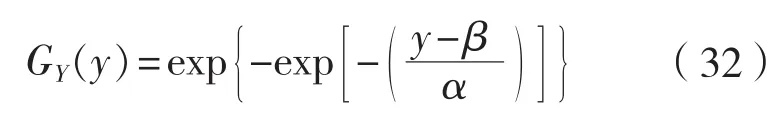
式中：和是Gumbel分布的参数，它们可以通过经验累积分布的一般拟合得到，如概率纸上最小方差拟合、求矩方法或最大似然方法等。

CHAI W等采用Gumbel方法估算参数，对于低水平超越概率，给出相应的极值如下：

上述2种方法均基于参数分布函数，而ACER方法通过构建不同阶次的ACER函数进行极值分布估算，ACER函数对稳态或非稳态数据系列均适用，有载荷峰值时间序列，极值可表达如下：

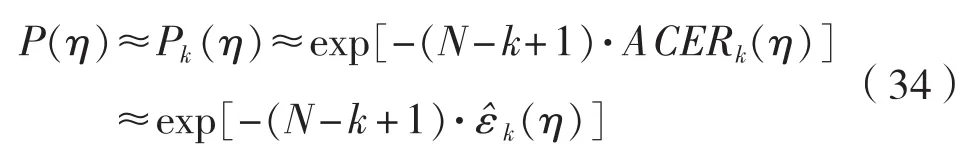
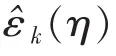
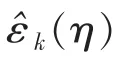
图42 点L4不同阶次k的ACER函数

图43 基于的点L4冰载荷极值预报

进一步采用Gumbel方法（= 5 min）来预报L4点上收集到的冰载荷峰值，相关概率值如图44所示。这个工况下90%分位值是244.5 kN/m，这高于ACER方法得到的188.4 kN/m。有2个原因来解释此差别：一是Gumbel方法受异常值的影响，当样本数量减少时，这种趋势会增强；二是按图示算例可见，采用线性回归法对样本数据进行概率拟合的整体效果并不尽如人意。因此渐近法的主要弱点是渐近极值理论本身不能判断它对于什么程度的观察数据可用。

图44 基于L4位置分时段（5 min）样本的Gumbel方法极值预报

基于不同位置收集到的冰载荷峰值时间序列，ACER方法和Gumbel方法预报得到的冰载荷极值如图45所示，这表明Gumbel方法对某些工况能提供满意的极值预报，但是预报好坏取决于不同位置的观测数据，2种方法预报的极值差异（如L1和L4）是由ACER方法和Gumbel方法背后的原理不同引起的。

图45 在6 h航程中，不同位置收集得到的冰载荷峰值的90%分位值

5 冰载荷实船测试研究总结

本文主要梳理和总结了自2015年以来冰载荷实船测试方面的研究成果，包括冰载荷实船测试参数、仪器和方法，将测试数据换算为冰载荷的方法，冰载荷的影响因素和空间分布特征，冰载荷概率模型和极值预报方法等。这些文章涉及多型极区航行船，包括救生艇、冰区调查船、海岸警卫船、LNG船、化学品船和极区供应研究船等，主要海域包括波罗的海、北极、南极和纽芬兰等。主要结论如下：

（1）为获取冰载荷主要测试首部外板、肋骨等应力、变形和船体运动等参数，总体来看船体应变监测和影响系数法最为广泛应用，获得的成果最多。船体运动监测和MOTAN系统有少量应用，但是换算结果误差相对较大，而船体损伤数据较少且只能反应遭遇的最大载荷，很难对冰厚、船速等进行相关性研究。

（2）冰载荷主要跟冰厚相关，随着冰厚的增加而增加，与航速有一定的相关性，但不是单调递增或递减。一般冰载荷最大值发生在3~7 m/s航速范围内，这可能是由于当主机功率一定时，冰厚增加使得船体所受阻力增加，很难进一步获得更高航速。

（3）冰载荷具有较强的空间分布特性，冰载荷平均压力与面积大小强相关，舷侧肋骨所受的载荷通常可看作沿水线分布的空间线载荷。随着冰载荷面积或长度的增加，中心区域的压力或载荷值会随之增加。

（4）在冰载荷概率模型和预报方法上取得了大量的成果，在冰压力、线载荷概率模型方面进展较快，但是极值预报方法往往与船型密切相关，要推广应用到实船设计还需要更多的数据积累和理论探讨。