基于不确定指数O-U过程带有浮动利率模型的亚式期权定价

刘兆鹏

(宿州学院 数学与统计学院,安徽 宿州 234000)

0 引言

期权定价在现代金融中扮演着重要的角色。亚式期权是一种强路径依赖期权，其收益取决于期权合约存续期内标的资产价格的平均值，亚式期权可以规避到期前市场操纵所带来的风险，是最受欢迎的奇异期权之一。

以往学者对亚式期权定价的研究主要是基于概率论，在Black-Scholes模型的假设下，获得了一些有用的结论，具体可以参看文献[1～3]。然而，在现实的金融市场中，由于信息不对称，投资者无法获得足够的数据来解决投资选择的问题，他们更愿意依靠以往的经验来做出自己的决定，因此信度在金融决策中起到非常重要的作用。为了理性描述信度问题，刘宝锭提出了不确定理论。基于股价波动遵循几何刘过程的假设，Liu[4]开始了不确定金融的研究工作，建立了不确定股票模型并推导出欧式期权定价公式。此后，许多学者致力于不确定理论框架下的金融问题研究。例如，Peng和Yao[5]研究了一种新的不确定股票模型；Yao[6]给出了基于不确定均值回复股票模型的无套利定理。此外，Yao[6]推导出股票模型无套利的充要条件，Yao[8]研究了浮动利率股票模型的应用；Zhang和Liu[9]研究了不确定金融市场下几何亚式期权定价问题；Sun和Chen[10]提出具有浮动利率的不确定均值回复模型，推导出亚式期权定价公式； Lv和Liu[11]提出一个新的带有浮动利率的不确定股票模型，并推到了欧式、美式和亚式期权定价公式；Wang和Chen[12]推导出具有不确定CIR浮动利率的亚式期权定价公式等。

本文基于已有文献，提出一种新的不确定股票模型，假设股票价格服从不确定指数O-U过程，利率服从不确定均值回复模型，分别推导了亚式看涨期权和看跌期权的定价公式，设计了计算期权价格的数值算法，并给出数值算例。

1 不确定理论

不确定性理论已经成为公理数学的一个分支，用来处理主观信念的程度。本节将介绍不确定变量和不确定微分方程的一些基本概念和定理。

定义1[4,15]L是非空集合(全集)Γ上的一个σ代数，集函数M:L→[0,1]如果满足规范性公理、对偶性公理、次可加性公理和乘积公理，称M为不确定测度。

Liu[4]给出不确定变量是ξ从不确定空间(Γ,L,M)到实数集上的一个可测函数，即对任意的Borel集，{ξ∈B}是一个事件。记Φ(x)=M{ξ∈x},x∈R，为不确定变量ξ的不确定分布；一个不确定分布Φ(x)被称为是正则的，如果Φ(x)(0<Φ(x)<1)是一个连续的严格单调函数，且有limΦ(x)=0,limΦ(x)=1，而Φ(x)的反函数Φ-1(α)称作ξ的逆不确定分布。

引理1[14]ξ是具有不确定分布Φ的不确定变量。 若它的期望存在，则

定义3[16](Γ,L,M)为不确定空间，T是全序集(时间)。 一个不确定过程是从T×(Γ,L,M)到实数集的函数Xt(γ)，使得在任意时刻t对于任意一个Borel集B,{Xt∈B}都是一个事件。

定义4[4]不确定过程Ct如果满足以下条件，则Ct被称为典范Liu过程:

(i)C0=0而且几乎所有的样本轨道是Lipschitz连续的；

(ii)Ct是平稳独立增量过程；

(iii)每一个增量Cs+t-Ct都是期望为0，方差为t2的正态不确定变量。即典范Liu过程的正态不确定分布和正态逆不确定分布分别是

定义5[4]若Ct典范Liu过程，f和g是两个给定函数，则dXt=f(t,Xt)dt+g(t,Xt)dCt,称为不确定微分方程。

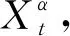
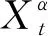
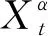
Liu[13]指出X1t,X2t,…,Xnt是独立的，如果对于任意的正整数k和任意时刻t1,t2,…,tk,不确定向量ξi=(Xit1,Xit2,…,Xitn),i=1,2,…,n是独立的。

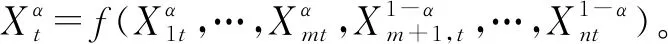
2 模型和主要结论

2.1 模型假设

在金融实践中，利率是一个重要的经济指标，经常受到一些不确定因素的影响,在探讨期权定价时，有必要考虑浮动利率。Yao[8]提出了带有浮动利率的如下股票模型：

(1)

其中rt为利率，Xt为股票价格，μ1,μ2,σ1,σ2是非负实数，C1t和C2t是相互独立的典范Liu过程。

模型(1)考虑的是股票价格的短期波动。长期来看，利率和股价应该围绕某个均值水平上下波动，为此，Sun和Su[13]提出了带有浮动利率的不确定均值回复股票模型：

(2)

其中rt为利率，Xt为股票价格，m1,m2,a1,a2,σ1,σ2(a1,a2≠0)是非负实数。

模型(2)可以反映出股票价格的均值回复特征。但是模型(2)是一种线性均值回复模型，为了更贴近现实金融市场，Dai[18]等人提出了非线性均值回复特征的不确定指数O-U模型。

(3)

其中r为利率，Yt为债券价格，Xt为股票价格，r,c,σ,μ是非负实数。

指数O-U过程是一类保证股价非负且具有回复水平的过程，它保证了股价在短期内不会发生巨大波动，有利于投资者进行投资决策。

本文将对以上模型做一些改进，提出一种新的具有浮动利率的不确定指数O-U股票模型：

(4)

其中rt为利率，Xt为股票价格，a,b,c,μ,σ1,σ2是非负实数,C1t和C2t是相互独立的典范Liu过程。

股票价格遵循指数O-U过程，避免了传统对数正态分布中股票价格随时间单向变化的限制，而利率服从均值回复模型，可以反映出利率围绕均值波动的特性，因此股票模型(4)更符合实际金融市场。

2.2 亚式期权定价

现基于新的不确定股票模型(4)，分别考虑亚式看涨期权和看跌期权，股票价格为Xt，执行价格为K，到期日为T。

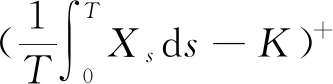
定理1假设执行价格为K，到期日为T，亚式看涨期权基于模型(4)的期权价格为

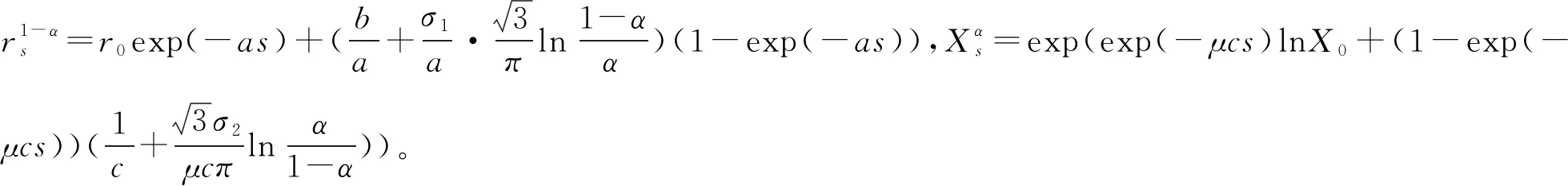
定理2假设执行价格为K，到期日为T，亚式看跌期权基于模型(4)的期权价格为

3 数值算法

根据定理1和定理2，计算亚式期权价格的数值算法设计如下：

根据要求的精度选择两个较大的数N和M，令αi=i/N，i=1,2,…,N-1,ti=j·T/M,j=1,2,…,M。

(1)令i=0；

(2)令i←i+1；

(3)令j=0；

(4)令j←j+1；

4 结束语

本文在不确定理论的框架下讨论了亚式期权的定价问题。首先提出了一个新的不确定金融模型，假设股票价格遵循不确定指数O-U过程，利率服从不确定均值回复模型，分别推导出亚式看涨期权和亚式看跌期权定价公式，为了对价格进行数值计算，设计了一些算法，并通过数值算例验证了算法的有效性，以期为金融决策和风险管理提供科学指导。