考虑数量折扣的多中心仓库联合采购-配送集成优化研究
2022-03-15王思睿王志刚曾宇容
王思睿 王 林 王志刚 曾宇容
(1.华中科技大学 管理学院, 湖北 武汉 430074; 2.湖北经济学院, 湖北 武汉 430205)
0 引言
联合采购问题(Joint Replenishment Problem, JRP)是指多个零售商通过一个中心供应商对多种商品进行分组集体采购,从而分担主要订货成本,节约采购总成本。在过去的几十年中,JRP的学术价值和实用性得到了广泛的认同[1-2]。在企业采购管理实践中,当一组物品都是由同一供应商或供应地供应,或一组物品同时采用一种运输工具运输时,特别适用于联合采购策略。例如,对我国大型电站的一些专用成套设备(如核电核能反应堆、大型水电站关键设备)而言,所用备件往往为不常用备件,由于技术的制约,经常面向国际环境进行采购。而且设备的制造商往往就是备件的供应商,非常适用于联合采购策略。课题组在大亚湾和岭澳核电站进行的一项备件联合采购优化的前期结果表明,该策略可降低8%~12%的成本[2]。而在公共采购领域,联合采购策略也十分流行。例如,2017年中国残联的数据显示,从2011年到2016年政府通过联合采购策略,大幅降低了物资采购价格,仅相当于市场价格的30%左右;2018年到2020年,国家医保局主持了跨区域、跨省份的药品联合带量采购联盟,药品价格平均降幅达到52%。在学术上,不少学者对经典JRP进行了扩展,一类扩展是放松经典JRP的假设或者调整约束,如:Moon等[3-4]讨论了供应商提供数量折扣的JRP和存在资源约束的JRP,Wang等[5]讨论了模糊参数的JRP、Boctor等[6]讨论了动态需求下的JRP,Chen等[7]讨论了运输车辆与运输约束的JRP,张云丰等讨论了[8]非瞬时补货下改良品的JRP;另一类扩展是将JRP与其他决策问题相结合,比如将JRP与选址-库存问题(Location-Inventory Problem, LIP)结合的联合采购-选址库存问题(JR-LIP)[9]、将JRP与配送相结合的联合采购-配送问题(Joint Replenishment and Delivery,JRD)[10]。尽管JRP问题应用广泛,但在早期JRP的研究中,扩展问题的研究主要集中在第一类扩展,而第二类扩展则比较少,而伴随着企业对精益化管理的要求以及成本压力的上升,最近十年联合采购-配送集成优化问题得到了广泛的关注,这也是本文研究重点。
将联合采购与配送相结合的JRD模型是非常具有现实意义:一方面这符合供应链协同管理的原则,贴合企业的实际情况;另一方面通过联合采购策略整合配送资源可以取得规模经济效应,可降低企业的配送成本。因此,JRD自提出以来就得到了许多学者的关注,如:Qu等[11]考虑异质品的JRD,Cui等[12]研究改进配送策略的JRD以及高效求解算法,Liu等[13]研究多个中心仓库的M-JRD模型,崔利刚等[14]等将JRD与RFID投资决策相结合。目前JRD问题还有较大的拓展研究空间,特别是还没有同时考虑数量折扣、资源约束、多中心仓库运作等贴近企业管理实践的因素。从现实性考虑,联合采购策略的一个目的便是实现数量折扣,这也是现实中采取联合采购策略时常考虑的一个因素,由于多种商品被联合订购,必然会加大采购的总数量/金额,有机会争取到较大的数量折扣。同时已有的研究表明,资源约束对于JRP问题的影响较大[4],如果不考虑资源约束,模型假设会与实际情况产生较大的偏差。而将JRD与多中心仓库的选址决策进行集成优化则非常有现实意义,如前文讨论的医药行业兴起的跨区域联合带量采购问题,在这类运营模式中,由一个统一的采购联盟负责管理所有消费者所需物资的采购,在获得数量折扣的情况下通过联合采购策略节省补货成本;由于最终用户可能分布在相距几百公里的地区,如果要保证物资交付及时,将会产生高额的运输费用,需要从多个候选点中选择合适的地点建立恰当数量的中心仓库,并确定中心仓库的最佳服务方案和最优的订货策略。因此,基于多中心仓库的多物品联合采购-配送集成优化模式是一种常见且有效的运营策略,这样使得供应链具有更好的柔性。
因此,本文拟研究考虑资源约束与数量折扣的M-JRD模型(M-JRD with Resource Constraint and Quantity Discount,CD-M-JRD),本文的问题与文献[3-4,13]较接近,然而文献[3-4]都没有考虑配送阶段的优化,并且是分别考虑资源约束和数量折扣,文献[13]则是没有考虑资源约束和数量折扣,因此应用价值都比较有限。文献[3-4]没有集成配送决策,未综合考虑多种资源约束,这可能会导致模型与实践产生较大偏差,故本研究将分别研究联合采购和配送阶段的资源约束对决策结果影响程度的大小,尤其是问题规模较大情形下,期望获得有益的管理启示,比如若联合采购的资源约束明显的话,企业决策者可加大在联合采购阶段的基础设施投资,如引进RFID技术[14]等。另外,本研究还将探索资源约束与数量折扣之间的相互影响,期望明确不同资源约束和问题规模时,数量折扣对降低成本的贡献是否显著。在企业实践中,如果不深入考虑这种影响,所构建的模型往往也难于成功应用。此外,尽管文献[13]基于武汉的三个大型中心仓库进行了一项优化研究,但没有对多中心仓库的情况进行成本的边际分析,多中心仓库运营模式的采用能给系统带来多大的成本节约也是一个有待深入研究的问题。综上所述,CD-M-JRD的研究具有较重要的学术价值。
作为典型的NP-hard问题[10],JRD问题属于混合整数非线性规划,问题难度较大,目前不存在有效、通用的精确算法。传统的数学规划方法并不适用,对问题的精确求解一般采用特定的枚举法,而对于中规模的问题(商品数量大于50)便已经很难求解[15],本研究集成了多种假设,数学模型相较以前的研究更加复杂,从而对求解算法提出了更大的挑战。因此,本文还分析了最优解的数学性质,得到了最优决策变量的界限以及原问题的拉格朗日松弛界限,并根据这两类性质设计了两种高效的求解算法,以供参考。
故本文的贡献如下:构建了一种考虑资源约束与数量折扣的多中心仓库联合采购-配送新模型;通过分析模型的数学性质设计了两种启发式的算法;针对不同的资源约束和中心仓库数量,进行了大规模算例的敏感性分析,获得一些有益的管理性启示如下:(1) 数量折扣与资源约束之间存在影响关系,当资源约束较为宽松或者采购的物品数量较少时,数量折扣能够有效的降低成本,而当物品规模较大、资源约束限制明显时,数量折扣作用减弱;(2) 联合采购阶段的资源约束对成本的影响非常大,而配送阶段的资源约束对成本的影响非常小,企业决策者应该多投资联合采购阶段的设施,扩大运输能力;(3) 增加中心仓库能有效降低成本,但其效果存在边际收益递减的现象。更详细的结论列于第4章,这些结论能为企业采购-配送集成优化提供科学的决策参考。
1 问题描述及模型建立
考虑一个包含m个中心仓库、n个供应商、n个零售商的多中心JRD模型,如图1所示。每个中心仓库基于下游需求从上游供应商处联合采购商品,然后将商品再由中心仓库以一定频次发送到下游零售商处。在模型中,每个供应商只能供应一种商品,同时每个零售商只能采购一种商品,每种商品只由一个中心仓库采购(根据Wang等[17]的证明,由I(I>1)个供应商和J(J>1,IJ)个零售商组成的 JRD 模型中,即使每个零售商能从任意多个供应商处采购不同商品,这个模型也总能转化为一个供应商与零售商相等且每个零售商只从一个供应商处采购一种商品的模型,也即是说我们的模型是一个通用模型)。模型考虑了每种商品的数量折扣,也加入联合采购阶段和配送阶段运输配送的容量限制。系统优化目标是找出使整个系统费用最小的采购、库存与配送方案。
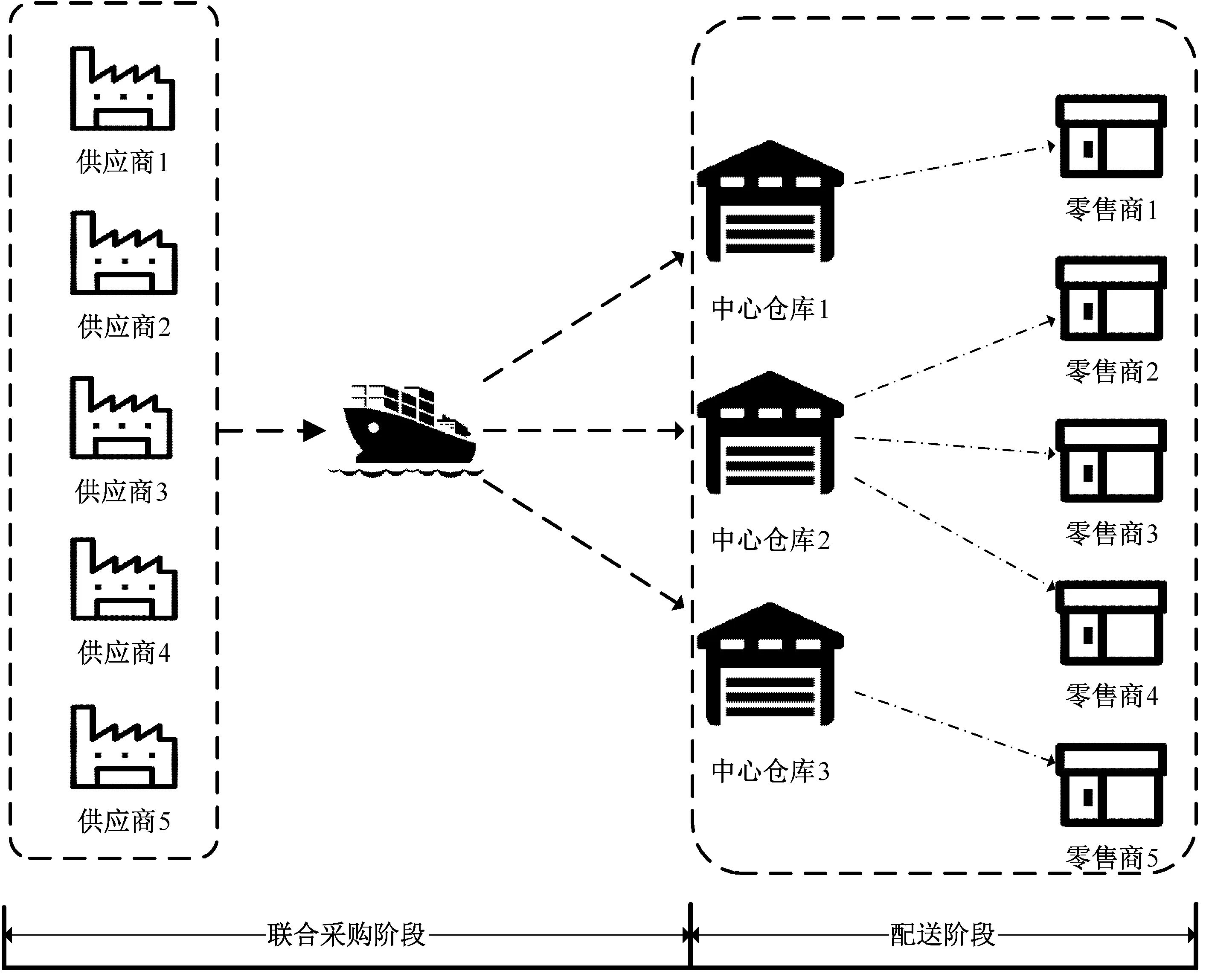
图1 CD-M-JRD结构图Figure 1The structure of CD-M-JRD
与基本JRD[10]和M-JRD[13]等模型假设相同,CD-M-JRD模型也采用以下假设:(1) 需求与各种费用为常数且已知;(2) 不允许有缺货;(3) 每个中心仓库不存在容量限制;(4) 不考虑中心仓库的建设成本。相关参数定义如表1所示。

表1 符号标示Table 1Notations used in the model
在考虑数量折扣的情况下,总成本由两大部分构成,分别是M-JRD的基本成本和考虑数量折扣后增加的商品成本,下面对相关成本分别分析:
1) M-JRD的基本成本TC1
总订货成本Cs,中心仓库的总库存成本Cwh,向零售商配送的成本Co,零售商的库存成本Crh,这四部分构成了基本成本:

2) 考虑数量折扣的商品成本TC2

其中Ci(ki,j,T)为商品i通过第j个中心仓库的采购价格,一般来说,数量折扣的边际增长是递减的,故∀i∈N满足:

由式(1)和式(2)可得总成本函数:

另外还必须考虑以下约束条件:K、F为正整数,X为0-1变量,联合采购阶段和配送阶段的商品重量不得超过最大运载能力,每种商品只能通过一个中心仓库采购。将以上内容归纳总结,可得到CD-M-JRD的数学模型如下所示,这是一个混合整数非线性规划问题。

2 决策变量的界限分析
CD-M-JRD模型中的决策变量有四个:K、F、X、T,其中K、F、T的最优上界是难以确定的,如果能对部分决策变量的上下界进行一定分析,将能够有效缩小算法的寻优空间,使得算法便于找到更好的解。文献[17]就提出了一种针对经典JRD的定界算法用于寻找决策变量的最优边界并取得了非常好的效果,在大规模算例上,这种效果尤为明显。因此,有必要针对CD-M-JRD的决策变量进行分析。
为了便于表达和推导,以下定义多个等式,并规定和分别代表变量G的上界和下界,「G■为大于或等于G的整数。
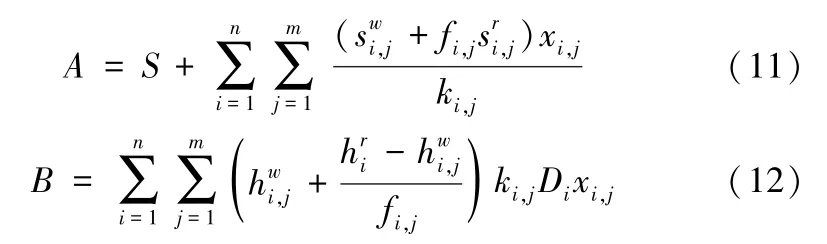
2.1 最优T的性质
命题1对于任意给定的K、F、X,定义T1= 2A/B,Ti,l=qi,l/(Diki,j),Tr= min (T2,T3),T2=Bw/其最优基本周期一定在(0,Tr]内。如果Tr<T1,那么最优基本周期为T*=Tr;如果T1<Tr,那么最优基本周期为(Ta)),其中Ta包括T1和Ti,l(满足条件T1<Ti,l<Tr)。
证明:首先由于两个资源约束条件,因此T*∈(0,Tr]成立,然后分两种情况:
(1)如果Tr<T1,则最优基本周期T*满足T*≤Tr<T1,对于任意给定的K、F、X,TC1为凸函数,T1为其最小值点,TC2为递减的阶梯函数,那么在(0,Tr]上TC为减函数,此刻必然在Tr处取得最小值。(2)如果T1<Tr,由于数量折扣的存在,最优基本周期T*满足T1≤T*≤Tr,在这个区间内TC1递增,TC2递减,因此T*必然为T1或大于T1的某价格断点Ti,l。
命题2对于任意给定的K、F、X,TC1的最优的基本周期T1满足如下条件:

其中,

证明:对于TC1而言,其最小值在处取得,故T1的一个界限为:

还可以发现以下关系:
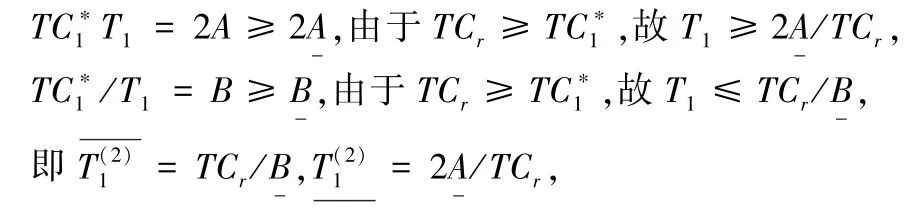
又因为对于最优的K、F,存在下面的不等式:

故有:

即

综上,T1的上下界为
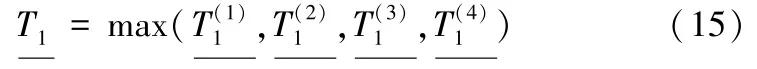

命题3对于任意给定的K、F、X,最优基本周期T*的下界满足
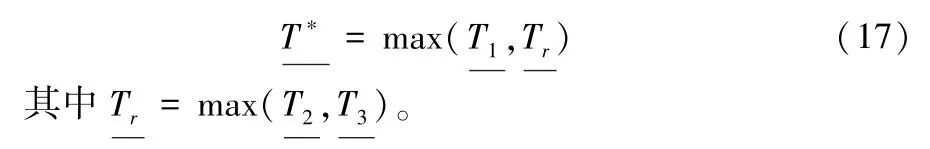
证明:根据命题1,T1是T*的一个下界,根据命题2,T1是T1的一个下界,故也是T*的一个下界。又因为要满足资源约束,故也是T*的一个下界。两者中较大者为T*的一个更严格的下界。
命题4对于任意给定的K、F、X,最优的基本周期T*的上界满足
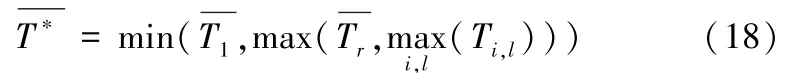
证明:根据命题1,T1、Tr的上界和Ti,l的上界中较小者为T*的一个上界,根据命题2可知T1的上界为的一个上界为
由命题3和4,显然对于任意给定的K、F,最优的基本周期T*′的界限为:

2.2 最优K的性质
命题5对于无约束问题,任意给定F、T,对应的最优K满足

证明:对于无资源约束的问题,任意给定对于任意给定F、T,可以使TC达到最优的K需要满足如下条件:

因此,K要满足下面的条件:

其中
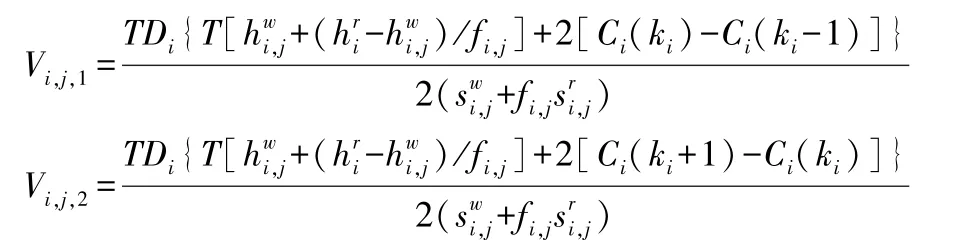
故最优的K满足

因此,对于任意给定F、T,TC对应的最优的K满足上式。
由命题5,我们还可以进一步得到无资源约束下TC1的最优的K:

其中

由此可得K的上下界:

2.3 最优F的性质
命题6对于无资源约束的问题,任意给定K、T,最优的F为

证明:对于无约束问题,最优的F满足
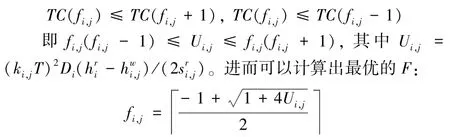
由命题6,还可以进一步得到F的一个界限
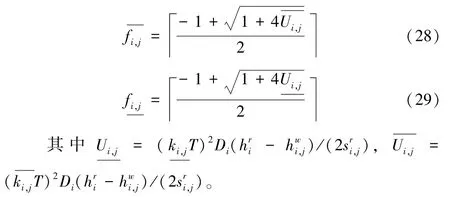
命题7对于存在资源约束的问题,任意给定K、T,最优的F为
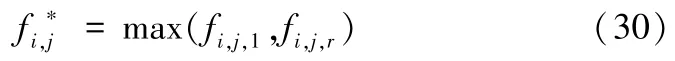
其中
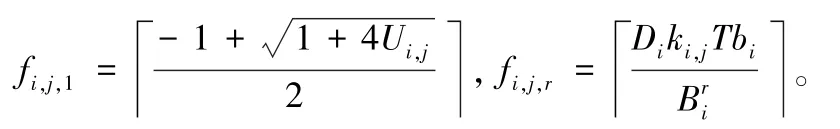
证明:由命题6可知fi,j,1为无资源约束下最优的F,由资源约束(8)可知0,TC(fi,j)为凸函数,故必为fi,j,1与fi,j,r中较大者。
2.4 最优X的性质
对于无资源约束的问题,任意给定的K、F、T,显然此时最优的X可以由以下的规划问题得到:
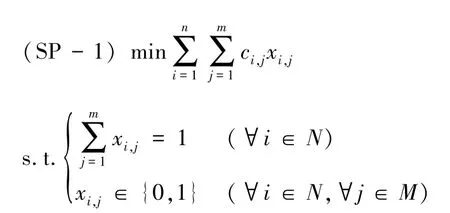
其中

对于这个问题,即使通过遍历,求解最优的X的时间复杂度也仅为O(mn)。
而对于存在资源约束的问题,由于命题7,我们可以先不用考虑资源约束(9),则存在以下规划问题:
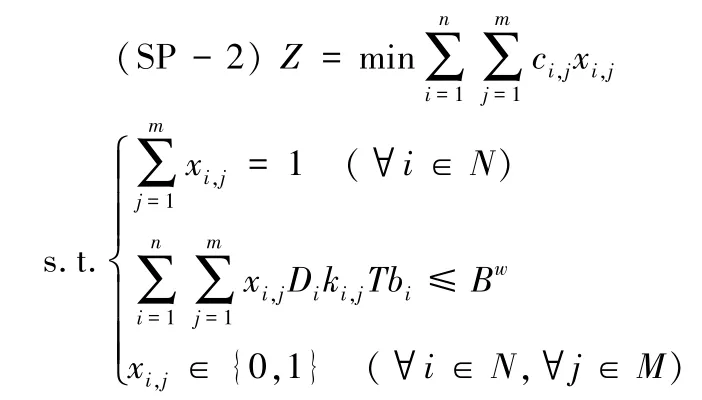
对于问题(SP-2),通过拉格朗日松弛放松资源约束(8),可以得到其松弛问题:
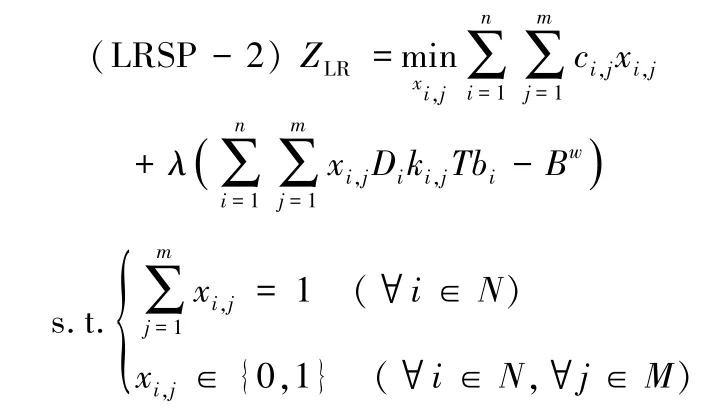
与(SP-1)相同,即使通过遍历,求解(LRSP-2)的时间复杂度也仅为T_,而对于其对偶问题:

可以采取一种次梯度法来进行求解,并采用以下的公式更新λ:

其中,0<ur≤2,UB为原问题(SP-2)的一个上界,显然如果(SP-2)存在可行解,一个上界为
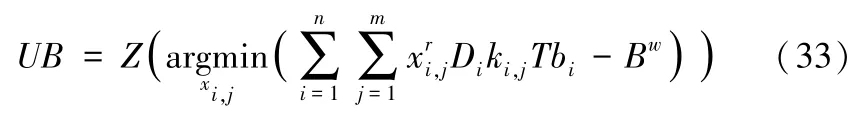
3 模型求解算法设计
JRD问题作为NP-hard问题,求解难度大,其求解算法的研究也一直是一个重要的研究方向,这方面的研究详见于Khouja的一篇综述[15],对于JRD问题的算法的设计一直有两种思路,一种是基于连续变量T,通过切割连续变量T,得到一个个固定的T的断点,对于每个断点进行迭代搜索,寻找最优的K、F, 代表性的算法是RAND 算法[10];另一种思路则是对整数变量K、F进行搜索,一旦固定一组K、F的值,再找到对应的最优的T的值,代表性算法是GA[10]和DE[11,15-16],如在文献[11]中自适应混合差分算法(Adaptive Hybrid Differential Evolution, AHDE)在求解复杂JRD问题上得到了目前最好的效果。由于JRD问题的结构,前一种思路适合设计结构化的启发式算法,对于一个固定的T值,可以设计各种领域结构或搜索策略来寻优;而后一种思路则适合以遗传算法为代表的进化算法,可以设置K、F的上下界,每一个变量作为遗传算法的一个基因,很简单地完成遗传算法的编码工作。没有明显的证据表明两种思路孰优孰劣,本文根据这两种思路设计了两种完全不同的算法:定界-自适应混合差分算法和M-RAND算法。
3.1 定界-自适应混合差分算法
定界-自适应混合差分算法的思想属于JRD问题算法的第二种思路,即首先通过定界算法缩小K、F的上下界,再通过算法进行搜索,本文采用了之前在JRD问题上取得了最好的效果的AHDE算法[11]来进行搜索。
3.1.1 定界启发式算法
对于CD-M-JRD问题来说,问题涉及的决策变量有K、F、X、T四部分,寻优空间非常庞大,并且由于K、F两个变量之间相互影响,其上界是难以确定的,常规的做法是直接设定其上界,K、F的上界常被设定为20,远大于Cha等[10]得到的最优解的5倍,由此来确保寻优空间包含了最优解,并且在文献[12][17]中这种设定都得到了很好的应用效果,但是当问题的规模扩大时,寻优空间呈指数级上升,如果仍然将K、F的上界直接设定为20,算法往往难以取得比较好的效果,这里就引入一种BH算法用于确定决策变量的边界,其思路如下:

(4) 循环步骤(1)-(3)直至K和F的界限收敛。
3.1.2 自适应混合差分进化算法
DE算法作为一种简单有效的进化算法,自提出以来[18]在众多领域得到了很好的应用[19],该算法主要包括三个操作:变异、交叉、选择,在DE基础上,AHDE算法在变异操作中引入自适应算子,在选择操作中使用改进的选择策略来加快搜索速度,已被证实是解决JRD问题的一种有效算法[11]。本文直接采用了文献[11]的AHDE算法,与DE相比,其改进主要有两点:
(1) 变异操作:差分算子采用如下自适应公式(34),其中g代表当前迭代次数,GenM代表最大迭代次数,Fmin和Fmax是事先设定的差分算子上下界,这种自适应算子使得算法能够在初期保持较大的种群多样性避免早熟,在后期则能够保留优良个体,加强局部搜索能力。
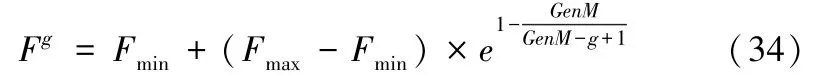
(2)选择操作:AHDE与DE“一对一”的选择策略不同,采用了局部截断的方式,这点与GA类似,具体来说,第g代种群经过变异交叉之后,根据适应度的优劣,留下其中一半的个体组成下一代种群,相比DE的“一对一”选择策略,这种选择策略往往具有更高的运算效率。
AHDE算法的其他详细步骤可以参考文献[11]。
3.1.3 定界-自适应混合差分算法流程
由于CD-M-JRD问题较为复杂,算法准确性和稳定性难以保证,本文通过将BH算法嵌套在AHDE中,设计了一种混合算法(下简称AHDE-BH)来解决CD-M-JRD问题。通过BH算法,可以使得寻优空间大大降低,使得AHDE能够搜索到更优的解,AHDE-BH的主要流程如下:
(1) 初始化:随机生成初始种群。
(2) 变异操作:根据公式(34)进行变异操作。
(3) 交叉操作。
(4) BH算法:根据章节3.1.1的BH算法流程,计算决策变量K、F的边界,从而缩小寻优空间。
(5) 选择操作:局部截断的选择方式。
(6) 判断终止条件:当迭代次数达到最大迭代次数时,迭代停止,否则重复步骤(2)~(5)。
3.2 M-RAND算法
本论文还基于JRD-RAND算法[10]的思想设计了一种M-RAND(Modified RAND)算法,算法通过切割连续变量T将问题转化为整数规划问题,并且对于每一个切割点,通过拉格朗日松弛界限来进行筛选,从而达到剪枝的效果,剔除掉一些切割点,最后对剩下的点进行求解。新算法的步骤可以总结为:
(1) 根据公式(18)(17)计算决策变量T的上下界,将其分为η-1个区间,区间断点为{T1,T2,…,Tl,…,Tη}。
(2) 通过启发式方法得到问题的上界,我们论文中选择计算T=Tη时的最优解TCη来得到上界。
(3) 对于每一个Tl,计算松弛问题(SP-1)得到下界,并进行剪枝:对于下界高于TCη的Tl不需要进一步寻优。
(4) 对于下界低于TCη的Tl,计算问题(SP-2)进一步寻优,所求解如果满足资源约束则结束,否则进行修复。
(5) 使用贪心算法对于不满足资源约束的解进行修复。
(6) 找到所有Tl中最优的解。
为了验证算法的效果,我们设计了3个实验。部分实验数据随机生成,生成规则参考文献[17]如表2所示,商品的单价参考文献[20]设定为6.25,价格折扣率根据实际情况设定为:数量超过25为0.9,超过50为0.8,超过100为0.7,bi根据文献[4]设定为6.25,所有算法采用 Matlab 2016b进行编码,算例都在一台配置为 Intel Corei7-4790K 4.0 GHz CPU, 16 GB RAM且操作系统为 Windows 7的个人电脑中完成。

表2 算例规则Table 2The range of parameters
4.1 实验1:不同商品规模下各种算法的性能表现
设计n= 10, 50, 100, 200 四种规模下的算例实验,每个规模随机生成20个算例,一共80个算例,所有算例的中心仓库数m=2、主要订货成本S为0.01倍的商品总价值、采购阶段的运输约束为25000、配送阶段的运输约束为2000。
在算法上选择DE、ADE、AHDE、GA(Genetic Algorithm)、PSO(Particle Swarm Optimization)、FOA(Fruit Fly Optimization Algorithm)来与AHDE-BH和M-RAND进行对比,原因如下:文献[21]已经证实在解决复杂JRD问题时,DE具有超过ACO、GA、JRD-RAND、JRD-SH的准确性和稳定性,而AHDE的性能也在文献[11]中有很好的体现,作为DE和AHDE中间变种的ADE之前则未有文献用于求解JRD,因此我们也纳入备选;GA作为一种经典的进化算法也在JRD的求解上有着出色的表现[10];PSO则作为与DE和GA不同思路的一种经典的群体智能算法在各种工程优化问题上被广泛应用[21];FOA则作为一种新型的群体智能算法在JRD的求解上也表现不俗[22]。除M-RAND外所有算法的最大迭代次数GenM=500,种群大小Np=100,M-RAND算法的η设定为1000,统计计算结果的平均值、最优次数占比以及算法的平均偏差如表3所示,几种算法在各种规模下的收敛表现如图2所示。

表3 各种算法得到的平均成本Table 3The average costs got by different algorithms
从表3可看出在问题规模较小时(n=10,50),AHDE-BH算法求解结果的偏差是最小的,也寻找到了最多的最优解,即使在n=100时,仍具有很好的性能,这说明了AHDE-BH算法的准确性和稳定性;而从图2不难看出,在收敛速度方面AHDE-BH也具有相对优势,考虑到实验的最大迭代次数GenM=500,已经较大,可以适当调小迭代次数,提高运算效率。另一方面,在问题规模较大时(n=100,200),M-RAND算法则效果最好,并且算法的运算效率非常高,求解n=200的算例只需要17.58秒,算法的偏差也较小,平均不超过0.01%,即使在计算小规模算例时也与AHDE-BH能相当,在大规模算例下,则明显比AHDE-BH好。从综合性能来讲,M-RAND算法更优,只有在计算小规模算例时,AHDE-BH具有微小的优势,但即使计算小规模算例时M-RAND算法的偏差也不超过0.01%。因此,对于小规模算例可以使用AHDEBH算法,而对于大规模算例,M-RAND算法更好。从算法的普适性来说,AHDE-BH的操作更加简单,更容易实现,面对其他扩展问题也有一定的普适性。从现有研究来看,计算决策变量K和F的界限是相对容易实现的[17],可以简单地套用这一套算法框架,即先缩小决策变量的界限再使用某种元启发式算法进行搜索;而M-RAND算法使用了较多的CD-M-JRD的模型特性,包括拉格朗日松弛下界和决策变量T的界限,操作起来更麻烦,也不容易扩展到其他问题中。
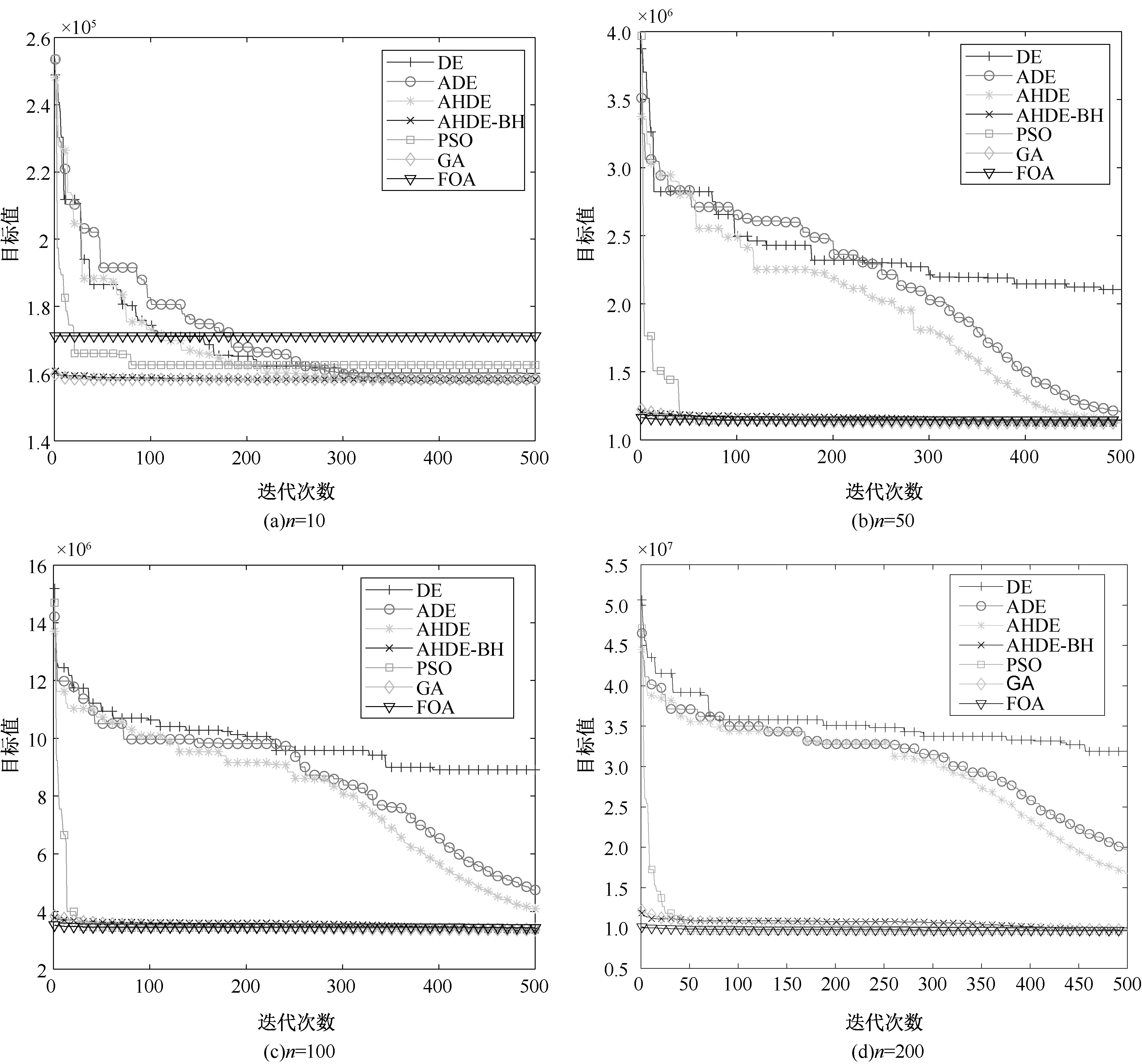
图2 不同规模问题下七种算法的收敛过程图Figure 2The converge plots of different algorithms under different problem scales
考虑到现实中,联合采购规模不能太大也不能太小,太大则管理困难,太小则规模优势不明显,n=50的规模与现实问题更接近,而AHDE-BH在n=50时展现了最好的准确性,因此在实验2和3中,仅使用AHDE-BH算法进行求解。
4.2 实验2:不同资源约束下的算例实验
为了进一步检验算法的性能以及资源约束和数量折扣对CD-M-JRD模型的影响,随机生成了一个n=50,m=2的算例,针对该算例设定了如下参数组合:主要订货成本S为0.01倍-0.05倍的商品总价值,资源约束Bw和Bri分别为1倍、5倍、10倍的M和N(M=25000,N=2000),一共45种组合,每种组合使用AHDE-BH算法重复计算10次,最后取10次中的最优值,计算结果如表4、5、6所示,从计算结果可以得到以下结论:

表4 Bw = M时的成本Table 4The result of Bw = M
(1) 采购阶段的运输约束Bw对成本的影响非常大,特别是对TC1的影响。与Bw=M的情况相比,Bw=5M,10M时,TC的均值分别降低到原先的49.54%和44.48%,TC1降低到22.32%和13.97%,TC2降低到91.19%和91.19%,产生这种情况的原因也不难理解,由于采购阶段的商品是所有商品一起采购,运输量非常大,Bw的影响就会非常明显,导致Bw=M时采购成本TC1甚至超过了商品自身成本TC2,但是一旦放松运输约束Bw,TC1和TC2都明显降低。
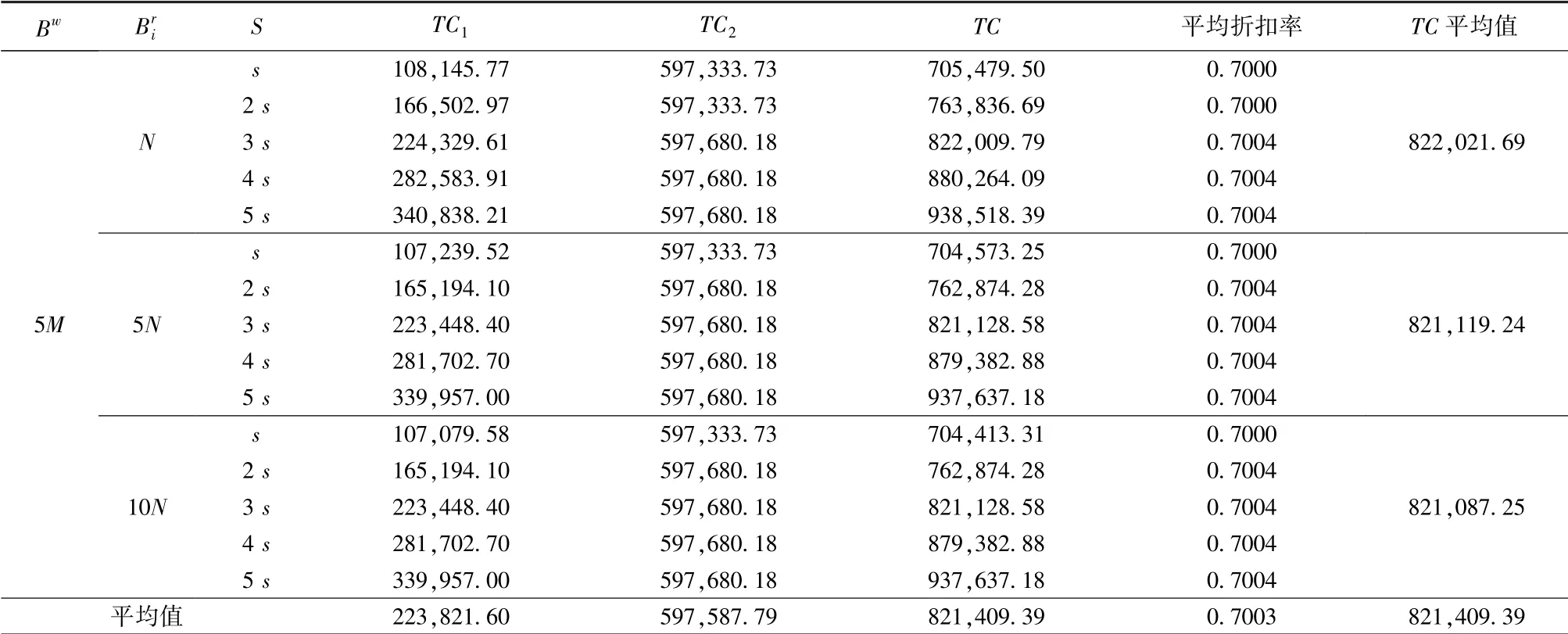
表5 Bw = 5M时的成本Table 5The result of Bw = 5M

表6 Bw = 10M时的成本Table 6The result of Bw = 10M
(2) 配送阶段的运输约束对成本的影响非常小。在Bw=M时,5N,10N并不能改变总成本的大小;Bw=5M时,TC的均值分别降低到原先的99.89%和99.89%;Bw=10M时,TC的均值分别降低到原先的99.90%和99.90%。产生这种情况的原因在于配送阶段对于每一个零售商的需求是分别配送的,这是不同于联合采购阶段的,因此每次配送量较小,除非约束条件非常严格,否则影响较小。
(3) 主要订货成本S对总成本的影响较显著,特别是对TC1的影响。在Bw=M,5M,10M三种情况下,与S=s的情况相比,S=2 s,3 s,4 s,5 s时:①TC的均值分别上升到原先的127.08%、154.17%、 181.25%、208.34%,TC1上升到169.33%、238.66%、307.99%、377.32%,TC2则没有改变;②TC的均值分别上升到原先的108.28%、116.54%、124.81%、133.07%,TC1上 升 到 154.09%、208.15%、262.35%、316.55%,TC2则为100.04%、100.06%、100.06%、100.06%;③TC的均值分别上升到原先的104.29%、108.58%、112.87%、117.15%,TC1上 升 到 135.58%、171.16%、206.75%、242.31%,TC2则不变。由于TC1是直接受S影响的,TC2则与S没有直接联系,因此产生这种结果比较好解释。并且值得注意的是S=2s,3s,4s,5s时,TC1每次增长的幅度基本保持在同一个水平。
(4) 数量折扣对成本有一定的影响。在Bw=M,5M,10M时,平均折扣率分别为0.7679、0.7003、0.7000,商品的成本能够有效降低,并且折扣率只对Bw的变化有明显的敏感性,对主要订货成本S的变化则不敏感。
值得注意的是,我们发现联合采购阶段和配送阶段的资源约束对于成本的影响是显著不同的,联合采购阶段的资源约束影响非常大,而配送阶段的资源约束影响则非常小,这对于联合采购-配送策略的一个现实问题:“投资决策”有很重要的指导意义[14],企业的投资应当优先满足联合采购阶段对运输、人力资源的需求。
4.3 实验3:不同中心仓库数量下的算例实验
在企业实际运作管理中,中心仓库的数量往往是多个的,为了研究中心仓库数量对模型成本的影响,设计了m=2,3,4,5四种情形的算例进行研究。为了避免个别算例影响实验结果,在随机生成m=2的算例后,我们在其数据基础上随机生成一个新的中心仓库的数据从而计算m=3的情况,同理去计算m=4,5的情况,算例均使用AHDE-BH算法求解,每个算例重复计算10次取最优值,主要订货成本S为0.01倍的商品总价值,资源约束Bw=25000,Bri=2000计算结果如表7所示,其中ΔTC(%)代表新增加中心仓库带来的成本变化及比例。

表7 多个中心仓库的结果Table 7The result of multi-warehouse
从表7的数据可以看出:存在更多中心仓库的模型成本更优,但增加中心仓库主要影响的是TC1,而对TC2没有影响;而且随着中心仓库数量的增加,增加中心仓库的边际效益是下降的,虽然本模型没有考虑中心仓库的建设成本或租用成本,但通过这种边际分析可以帮助企业决定是否建设或租用新仓库。
5 结论
本文的主要贡献如下:(1)设计了一种考虑资源约束与数量折扣的多中心仓库联合采购与配送模型,模型贴合企业实际情况,具有较好的学术价值和实用价值;(2)针对模型的数学性质进行了一定分析,得到了最优决策变量的较好的界限,并据此设计了两种求解算法,两种新算法在精度和稳定性上相较已有算法都有较明显的优势;(3)设计了不同资源约束以及不同中心仓库数量下的大规模算例实验,实验证明:联合采购阶段的运输约束Bw对成本的影响非常大而配送阶段的运输约束对成本的影响非常小,主要订货成本和数量折扣则对成本有一定的影响,增加中心仓库数量能够带来明显的收益,但具有边际效益递减的现象。根据这些结论,可得到以下管理启示:由于联合采购阶段的资源约束对成本的影响非常大,如果约束比较严格,数量折扣往往也难以实现,而配送阶段的资源约束则影响很小,故应该增加在联合采购阶段的投资,如购买更大更多的货运卡车或者采取RFID[14]等新技术提高联合采购阶段的能力;增加中心仓库确实能带来一些收益,尽管本文没有考虑中心仓库的建设成本,但从边际分析来看,增加中心仓库的边际收益是递减的,因此中心仓库不宜过多,从本研究实验结果来看,不宜超过5个。
未来拟将此模型拓展到不确定需求下允许缺货的情形或者在模型中考虑中心仓库的建设成本或租用成本[23],这样模型将变得更贴合现实,拟结合果蝇优化算法[24]或者帝国竞争算法[25]设计更高效的智能求解新算法。
