仅知需求区间信息下具有二次订货机会的损失厌恶报童鲁棒优化模型

邱若臻 曹沙沙 孙 月

(东北大学 工商管理学院, 辽宁 沈阳 110169)

0 引言

经典报童问题(又称为单周期库存问题),研究的是决策者在面对随机需求时,如何确定订货量以期获取最大利润。报童问题在经济管理活动中应用十分普遍,广泛应用于收益管理,库存管理,供应链契约及服务运作等运作管理领域[1]。传统关于报童问题的研究通常假设只有一次订货机会,即,决策者只能在销售季节来临前向上游供应商发出订货订单,一旦销售季节开始,即使出现缺货也不允许进行二次订货。然而,在实际运作中,为了降低报童的库存风险并实现较高的客户服务水平,供应商通常允许其下游零售商在销售季节中进行二次订货,该问题又被称为考虑追索权的库存优化问题[2]。比如时尚快消服装的零售商,在销售季到来之前向上游服装供货商以批量订购价格订货。如果销售期内某类紧俏服装的需求超过初始订单,出现缺货时,上游供应商允许零售商以高于初次订货单位成本的价格进行二次订货直至满足所有需求。

关于此类问题,Lau和Lau[3]建立了允许二次订货的报童模型,给出了报童决策者的最初订货量,以及需要二次订货时,何时订购及订购多少等决策,并进一步表明库存补货需要综合考虑订单处理成本、价格变化及资源限制等因素。Weng[4]在报童模型框架下,研究了具有二次订货机会的单制造商和单销售商协调订货问题。Zhou和Wang[5]在此基础上将模型扩展为当初次订货之后,由于市场出现过量需求导致销售商的产品短缺时,制造商和销售商共同分担二次订货成本时的供应链协调问题。禹海波[6]采用随机占优和可变序方法研究带有二次订货策略的最大利润报童问题,证明了只有当二次订货费用小于或等于零售价格时,随机大需求才会导致较高的利润。对任意二次订货费用,在二阶随机占优意义下系统最优利润随需求可变性增加而减小。Herbon等[7]针对具有二次定价和订货机会的销售报童类型产品的零售商,通过将销售周期划分为两个子周期,采用随机规划方法研究了基于延迟策略的定价和订货问题。

上述报童问题考虑了二次订货问题,但均没有考虑决策者的风险厌恶水平。实证研究表明,决策者实际采用的运作策略并不总是与基于期望利润或成本的策略一致[8]。因为决策者往往存在损失厌恶。作为前景理论的重要基础,损失厌恶是指人们对于损失和收益的敏感程度不同,面对同样数量的收益和损失时,认为损失更加难以忍受[9]。损失厌恶反映了人们对风险的偏好态度并不是一致的,当涉及收益时,人们表现为风险厌恶;当涉及损失时,人们则表现为风险寻求。针对报童决策问题,Schweitzer和Cachon[10]研究了损失厌恶对报童决策者订货量的影响,发现损失厌恶报童的订货量少于风险中性报童订货量。Wang和Webster[11]证明如果缺货成本较高,损失厌恶报童决策者的订货量要高于风险中性报童的订货量,并且损失厌恶报童订货量会随着损失厌恶系数的增加而增大。马德青等[12]研究具有损失厌恶和损失概率厌恶行为的报童问题,通过构建报童的前景值函数,分析了报童订货量决策随相关参数的变化情况。当考虑二次订货问题时,Ma等[13]通过研究在市场需求信息不断更新的情况下,损失厌恶报童决策者的二次订货决策,发现初次订货量与需求的不确定性有关,决策者会将初次订货和二次订货进行权衡来实现利润最大化,如果订单允许取消,则初次订货量将会更高。Vipin和Amit[2]研究了损失厌恶下的报童订货行为,发现损失厌恶的考虑能够有效改进所建模型在预测报童理性行为方面的绩效。

上述文献中无论是风险中性还是损失厌恶下具有二次订货的报童问题研究,均是基于已知不确定参数的完备信息。随着市场竞争环境的复杂多变,各种不确定因素日益加剧,特别是市场信息的快速变化,以及企业在掌握市场变化能力方面的局限性,使得基于完备信息的决策难以适应实际情况。自上世纪90年代以来,鲁棒优化方法被广泛应用于解决受不确定性扰动的供应链及库存决策问题[14]。针对报童问题,Scarf[15]最早采用绝对鲁棒性建模准则研究了在仅知需求均值和方差信息下的单周期报童订货问题,并给出了封闭形式的Scarf订货规则。在此基础上,一些学者在不同条件下进一步做了扩展性研究[16-18]。最近,Yu等[19]在损失厌恶下研究了仅知需求均值和方差条件下的报童订货策略,发现损失厌恶和风险中性下的报童鲁棒最优订货策略虽然不同,但损失厌恶对于鲁棒订货策略和传统订货策略的影响基本一致。在同样的条件下,张文思等[20]虑需求分布未知情况下含数量折扣的多产品库存与定价联合问题,建立了混合整数非线性规划模型并设计了求解算法。Park和Lee[21]针对损失厌恶优化问题,研究了仅知不确定参数部分信息的分布鲁棒优化方法。根据Roy[22],在进行鲁棒建模时有三种鲁棒性度量准则,即绝对鲁棒性、鲁棒偏差(又称后悔值准则)和相对鲁棒性。由于绝对鲁棒性仅关注最坏情况,导致该准则下的决策具有较高的保守性。为改进解的保守性,Yue等[23]在仅知需求均值和方差下,通过构建基于后悔值准则的报童优化模型,探讨了特定订货量和特定分布下的分布信息期望值问题。在此基础上,Perakis和Roels[24]采用后悔值准则研究了仅知部分需求信息(例如,需求区间、均值、均值和方差、中值等)的报童问题,给出了基于最小最大后悔值的订货量决策。Zhu等[25]进一步采用相对鲁棒性研究了仅知需求区间和均值以及均值和方差条件下的报童决策问题。

通过梳理已有研究发现,目前关于不确定条件下具有二次订货机会的报童决策研究还存在以下亟待解决的问题:(1) 在经典报童模型基础上,虽有相关研究考虑了二次订货问题,但通常基于已知需求具体分布形式假设,通过优化期望利润获得最优订货量决策。现实当中,完备需求信息通常难以精确获取,从而导致随机优化方法无法应用于需求信息缺失情况;(2) 已有关于报童鲁棒优化问题的研究在建模时多数采用绝对鲁棒性准则,该准则由于仅关注最坏需求分布情况而致使得到的订货量决策具有较高的保守性;(3) 为改进传统最大最小鲁棒解的保守性,Yue等[23],Perakis和Roels[24]提出了最小最大后悔值准则,用于度量鲁棒解和最优解之间的绩效偏差。该方法有效降低了基于最大最小准则的鲁棒解的保守性。但由于求解具有封闭形式解的复杂性,目前此类方法应用较少且主要集中于仅有一次订货机会的报童决策问题,鲜有文献采用该方法研究损失厌恶下考虑二次订货的报童决策问题。基于此,本文在已有研究基础上,采用最小最大后悔值准则研究仅知需求区间信息条件下考虑二次订货的损失厌恶报童鲁棒决策问题,得到了具有封闭形式的鲁棒订货量决策及由于需求信息缺失而未能采取最优决策导致的后悔值绩效。进一步,分析了损失厌恶系数、初次订货单位成本、二次订货单位成本、单位残值以及需求区间范围等系统参数对报童鲁棒订货量和后悔值绩效的影响,并给出了相应的管理启示。

1 基本问题描述

考虑一个销售季节性产品的损失厌恶报童决策者,其面临不确定市场需求x。假设市场需求x在区间[A,B]上具有服从某一类未知分布Ψ的累计分布函数F,F∈Ψ。为满足市场需求,在销售季节到来之前,决策者需要确定以单位价格w向上游供应商订购多少数量的产品,即确定订货量决策Q。销售季节开始后,需求实现,决策者以单价p出售产品。如果订货量大于市场需求,即,Q≥x,超出的部分只能在季末以单位残值v清仓处理;反之,如果订货量不足以满足市场需求,即,Q＜x,则考虑决策者具有追索权,即允许有二次订货的机会,但对于未满足市场需求的部分,报童决策者将支付较高的单位采购成本w^(w^＞w)。整个销售周期内的事件发生时间过程如图1所示。特别地,如果p=w^,报童将由于无利可图而不进行紧急订货,此时问题等价于经典的报童问题;如果w=w^,由于缺乏采购价格激励,报童将不会过多地承担销售季节来临之前采购所带来的库存风险,即在期初只少量订货或不订货。不失一般性,假设p＞w^＞w＞v≥0。

图1 事件发生顺序Figure 1Sequence of events

报童的收益函数如下:

当已知需求分布F时,最大化报童期望收益的最优订货量为:

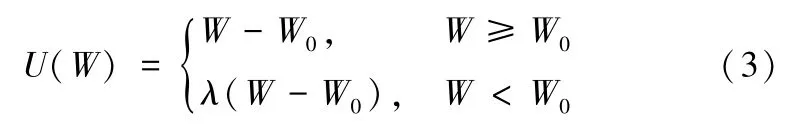
其中,W0为销售季节期初报童的参考水平,λ≥1是损失厌恶系数。当λ=1时,表明决策者是风险中性或损失中性的。λ越大,说明报童损失厌恶程度越高。根据Kahneman和Tversk[9],λ的取值通常为2.25。不失一般性,令W0=0。则在式(3)基础上,报童的期望效应函数为:

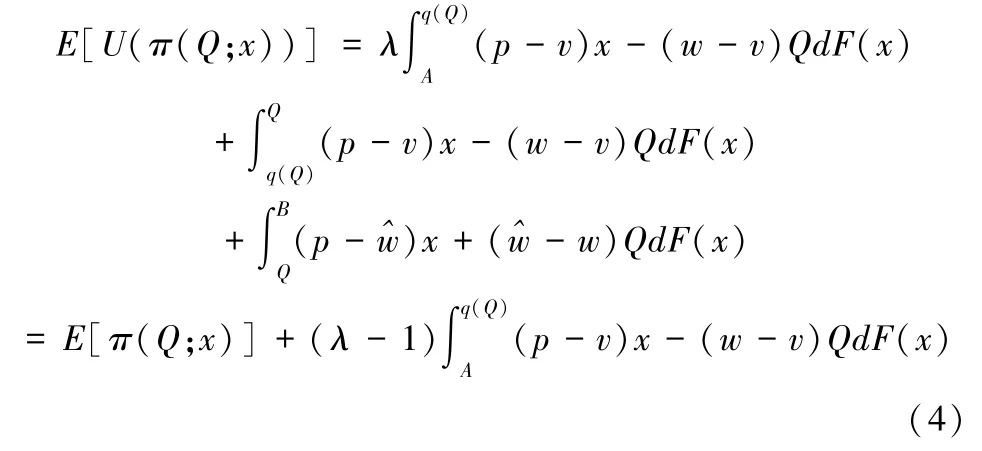
2 风险中性下具有追索权的报童鲁棒优化模型

当报童为风险中性(即,λ=1)时,根据式(1),报童的期望利润函数可表示为:

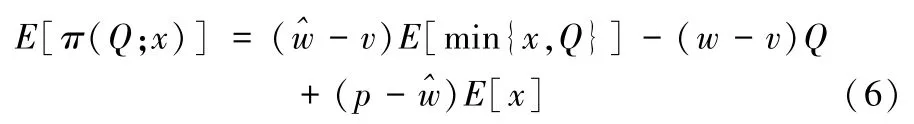
令Q0表示已知需求完备信息时的最优订货量,则当仅知需求区间信息时,报童订购Q单位的产品时所导致的后悔值为:

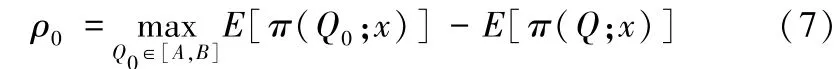
其中,ρ0度量了当知道需求分布具体信息时所能获得的额外利润,当需求分布F未知时,最大后悔值可以表示为:

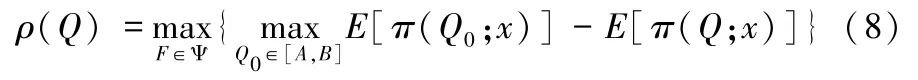
可以看出,最大后悔值ρ(Q)衡量了报童为获得需求完备信息所愿支付的最高成本。根据最小最大后悔值准则,报童决策者的决策目标为:

考虑如下式(9)内层优化问题,即

根据文[24]中命题1,有如下引理1成立。

引理1(1) 函数θ(Q0,Q;x)在区间Q0∈[0,Q]和Q0∈[Q,∞)上均是凹函数,但在区间Q0∈[0,∞)上并不一定是凹函数;

(2) 最大后悔值函数ρ(Q)是凸函数,则鲁棒订货量Q*=argminρ(Q),且有如下等式成立:

引理1中(1)表明,在求解问题(9)时,应分别考虑Q0≤Q和Q0≥Q两种情况;(2)表明,当由于实际订货过多产生的负效应值和实际订货过少产生的负效用值相等时,鲁棒订货量能够使最大后悔值最小化。

定理1当仅知需求区间信息,即x∈[A,B]时,基于最小最大后悔值准则的风险中性报童鲁棒订货量和最优后悔值分别为

证明:令g(Q0,Q;x)=min{x,Q0}-min{x,Q},根据引理1,分Q≤Q0和Q0≤Q两种情况讨论。

(1)Q≤Q0。当Q≤x≤Q0时,g(Q0,Q;x)=x-Q;当Q≤Q0≤x≤B时,g(Q0,Q;x)=Q0-Q;当A≤x≤Q时,g(Q0,Q;x)=x-x=0。因此,最大后悔值为:

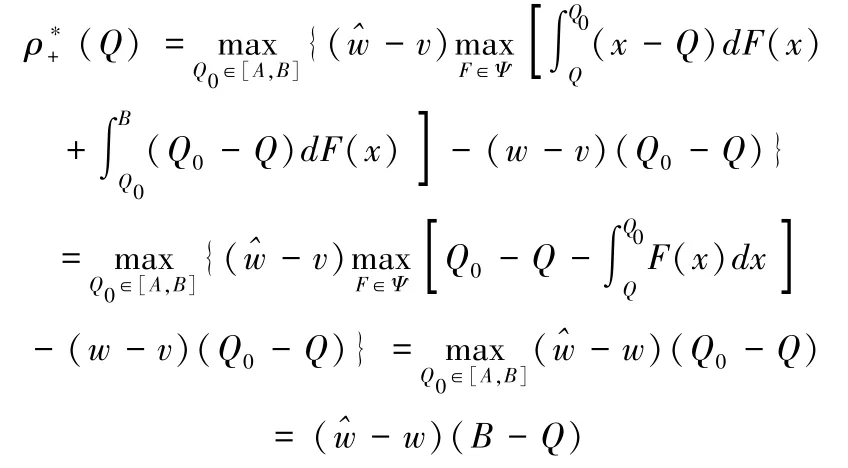
(2)Q0≤Q。当Q0≤x≤Q时,g(Q0,Q;x)=Q0-x;当Q0≤Q≤x≤B时,g(Q0,Q;x)=Q0-Q;当A≤x≤Q0时,g(Q0,Q;x)=x-x=0。因此,最大后悔值为:

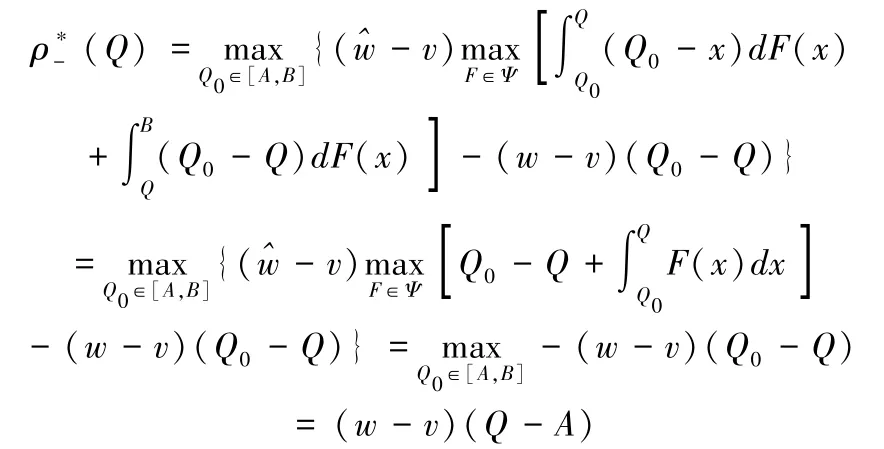
由定理1可以看出,当考虑追索权时,风险中性下的报童订货量及对应的后悔值绩效仅与初次订货成本w、二次订货成本w^、残值收益v及区间[A,B]有关,而与市场零售价格p无关,与传统仅允许期初订货的报童模型不同。这是由于当决策者观测到实际需求后,如果期初订货量难以满足实际需求,可以以较高采购价格补货直至完全满足市场需求,因此,决策者所能获得的销售收入即为完全满足市场需求x时的销售收入,可认为是一定值;而当期初订货量超出实际市场需求时,决策者所能获得的销售收入仍为一定值,即满足市场需求x时的销售收入,多余的部分将以残值v进行清仓处理。因此,考虑追索权的报童订货量及后悔值绩效并不受市场零售价格p的影响。进一步,当二次订货与初次订货单位成本相等时,即时,根据式(10),Q*=A,说明由于缺乏采购价格激励,决策者不会承担库存风险,因此只在期初订购最少数量的产品,与前文分析一致。

由于完备需求分布信息的缺失,定理1给出的订货量决策虽然不是最优的,但却是具有鲁棒性的。令ρ(Q)表示给定订货量Q下的最大后悔值,则对于任一决策准则(例如,均匀分布或正态分布)下的订货量,γ=ρ(Q)/ρ*衡量了其他决策准则与最小最大后悔值准则之间的优劣。根据文[33],对于经典报童模型,当仅知需求区间信息时,基于最小最大后悔值准则的鲁棒订货量等同于已知需求在[A,B]上服从均匀分布时的最优订货量。由式(2)可以看出,当已知需求服从均匀分布时,有,此时,因此,在需求分布信息缺失情况下,当允许报童进行二次订货时,可通过假定需求服从均匀分布进行决策。

推论1对于区间[A,B]上的任意非负累计分布函数F∈Ψ,有如下结论成立:

(1) 风险中性报童的鲁棒订货量Q*随初次订货单位成本w的增加而减小;

(2) 对于初次订货成本w,存在临界值当时,风险中性下的报童后悔值ρ*随初次订货单位成本w的增加而增加;当时,风险中性下的报童后悔值ρ*随初次订货单位成本w的增加而降低;当,风险中性下的报童后悔值ρ*与初次订货单位成本w无关。

证明:根据式(10),有推论1(1)得证。根据式(11),有可以看出,存在＜0;当推论1(2)得证。

推论1中的结论(1)容易理解,当期初采购价格较高时,由于允许二次订货,风险中性决策者势必会减少期初订货量以降低采购成本。然而,决策者因信息缺失而未能制定最优决策所导致的后悔值随初次订货成本的变化情况却并不单调。当初次订货成本w较低,例如时,后悔值随w的增加而增加;当初次订货成本w较高,例如,时,后悔值随w的增加而降低。特别地,当时,后悔值为零,这暗含此时的鲁棒订货量决策与最优订货量决策一致。因此,结合推论1(1),当w较低时,w越大说明鲁棒订货量决策越偏离最优情况,从而导致后悔值增加;反之,当w较高时,w越大说明鲁棒订货量决策越贴近最优情况,因此后悔值越小,如下图2所示。由图2可以看出,当上游供应商制定的初次单位采购价格低于临界值时,w越小对下游零售商越有利;而当初次单位采购价格高于该临界值时,w越大越对下游零售商有利。推论1暗含如下管理启示,即在允许二次订货条件下,与供应商进行采购谈判时一味地压低采购价格并非总是有利可图。实际上,只有当供应商给予的初次采购价格低于某一临界值时,零售商进一步压低采购价格才能获利。而当供应商初次采购价格高于该临界值时,价格越高反而对零售商越有利。

图2 鲁棒订货量和后悔值随初次订货单位成本的变化Figure 2Changes of robust order quantity and regret value with initial unit ordering cost

推论2对于区间[A,B]上的任意非负累计分布函数F∈Ψ,风险中性报童的鲁棒订货量Q*和对应的后悔值ρ*均随二次订货单位成本w^的增加而增加。

推论3对于区间[A,B]上的任意非负累计分布函数F∈Ψ,风险中性报童的鲁棒订货量Q*和对应的后悔值ρ*分别与单位残值v呈正相关和负相关关系,即单位残值越高,风险中性报童的鲁棒订货量越大,后悔值越小。

推论3的管理启示体现在如下几方面:(1) 从报童角度,由于较高的残值会显著改进其绩效,因此,报童决策者在日常经营过程中应提升其服务水平,通过提高附加于产品本身的服务价值确保产品在销售周期结束时具有较高的残值;(2) 从产品供应商角度,较高的残值无论是对于消费者还是其下游零售商都具有较高的吸引力,为了提高产品残值,供应商应注重产品价值的提升,例如,通过技术创新改进产品功能、提升产品质量等。另一方面,无论是下游销售商还是上游供应商,提升产品价值的一系列举措又会反过来刺激市场需求的增加,从而使双方获利。

推论4对于需求区间[A,B]上的任意非负累计分布函数F∈Ψ,当区间下界A固定时,风险中性报童决策者的鲁棒订货量Q*随着上界B的增大而增大;当区间上界B固定时,风险中性报童的鲁棒订货量Q*随着下界A的增大而增大;当区间上、下界均变化时,风险中性报童的鲁棒订货量Q*随区间范围的增大可能增加也可能减小。然而,风险中性报童的后悔值ρ*随区间范围的增大而增加。

证明:任取两个不同范围的需求区间[A,B1]和[A,B2],对应的订货量决策分别为和。不失一般性,假设B2＞B1,根据式(10),有如下结果

同理,任取两个不同范围的需求区间[A1,B]和[A2,B],对应的订货量决策分别为和。假设A2＞A1,根据式(10),有

当区间[A,B]的上下界均变化时,任取两个需求区间[A1,B1]和[A2,B2],对应的订货量决策分别为和,假设B2-A2＞B1-A1,则根据式(10),有

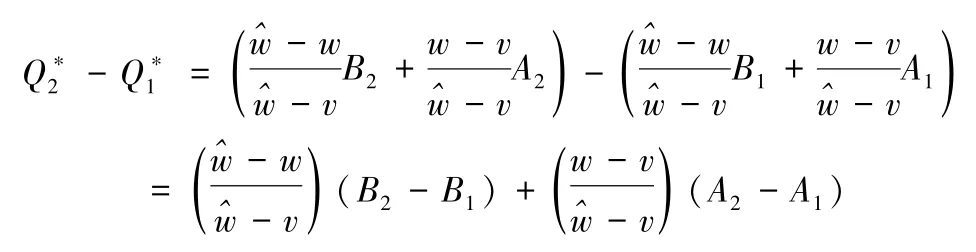
由于B2-A2＞B1-A1,分三种情况进行讨论:(1) 当当B2＜B1,A2＜A1时可能大于0也可能小于0。进一步,根据式(11),有说明后悔值随区间范围的增大而增加。

从需求预测角度,需求区间范围的大小反映了决策者对需求信息掌握的准确性。通常,区间范围越小说明需求信息越准确。从推论4可以看出,报童的后悔值随需求区间范围的增加而增加,说明掌握的需求信息越准确,依此所制定决策下的后悔值绩效越贴近最优情况。然而,其订货量决策却与区间范围的大小没有直接关系。推论4的管理启示在于决策者应在日常经营过程中注重数据的收集和预测方法的改进,以提高需求隶属区间范围的精度,从而降低因难以掌握完备需求信息所带来的后悔值。

3 损失厌恶下具有追索权的报童鲁棒优化模型

当报童为损失厌恶时,即λ＞1,根据式(4),报童期望效应函数可描述为:

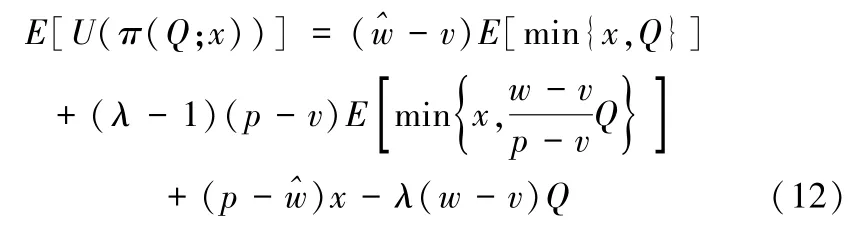
同理,令Q0表示已知需求完备信息时的最优订货量,则需求分布未知条件下的最大后悔值为:

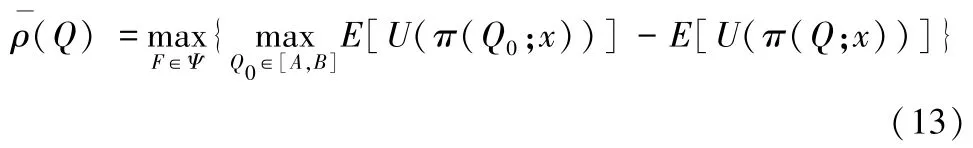
根据最小最大后悔值准则,报童的决策目标为最小化其最大后悔值,即

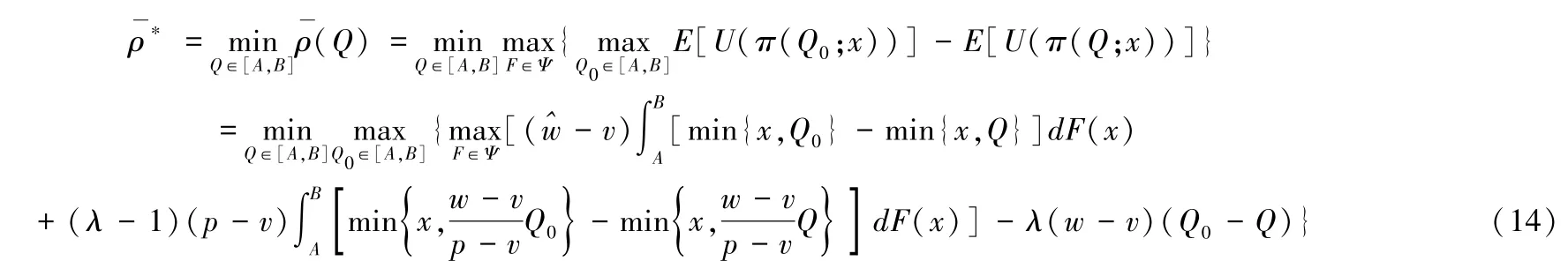
对比式(14)和式(9)可以看出,当考虑报童损失厌恶态度时,其决策目标进一步受损失厌恶系数和盈亏平衡点的影响。下述定理2给出了仅知需求区间信息时,损失厌恶报童的鲁棒订货量决策及最优后悔值。

定理2当仅知需求区间信息,即x∈[A,B]时,基于最小最大后悔值准则的损失厌恶报童鲁棒订货量和最优后悔值分别为:

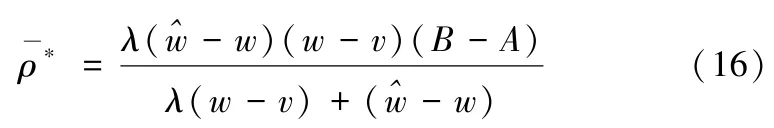
证明:令g1(x,Q0;Q)=min{x,Q0}-min{x,Q},g2(x,同上,分Q≤Q0和Q＞Q0两种情况讨论。

(1)Q≤Q0。当Q≤x≤Q0时,g1(Q0,Q;x)=x-Q;当Q≤Q0≤x≤B时,g1(Q0,Q;x)=Q0-Q;当A≤x≤Q时,g1(Q0,Q;x)=x-x=0。因此,

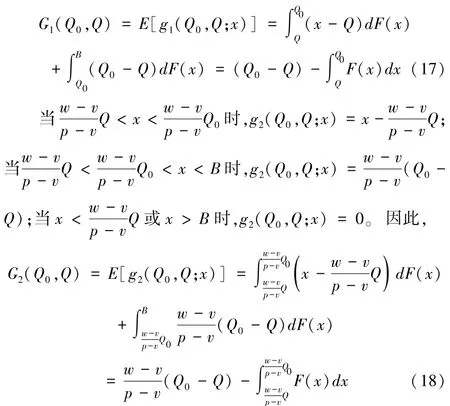
则相应的最大后悔值为:

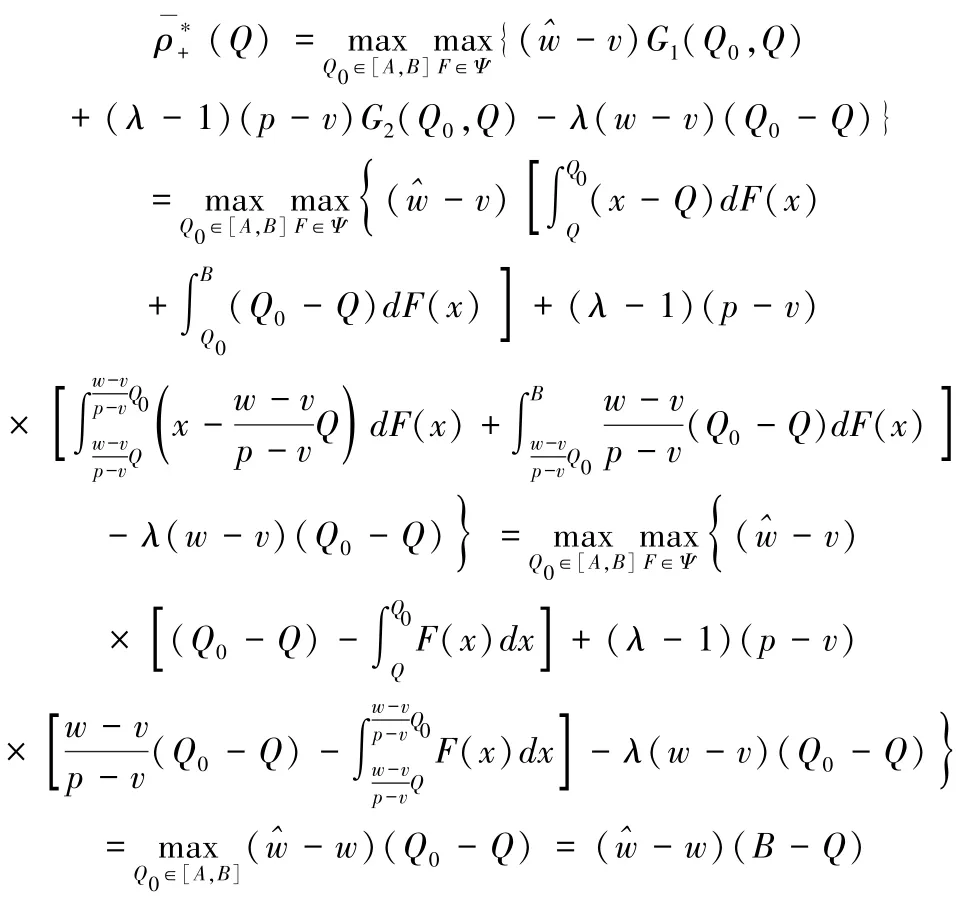
(2)Q＞Q0。当Q0＜x＜Q时,g1(x,Q0;Q)=Q0-x;当Q0≤Q≤x≤B时,g1(x,Q0;Q)=Q0-Q;当A≤x≤Q0时,g1(x,Q0;Q)=x-x=0。因此,

则相应的最大后悔值为:

由定理2可以看出,当时,,说明损失厌恶下,当初次定订货和二次订货单位成本相等时,具有追索权的报童决策者仍然只会在销售季节来临之前订购最少数量的产品。

当损失厌恶系数λ=1时,报童鲁棒订货量

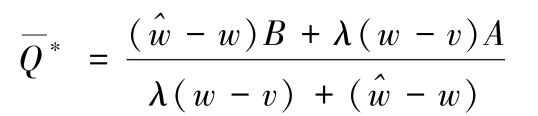
定理3损失厌恶 (λ＞1) 下的报童订货量低于风险中性 (λ=1) 下的订货量;而对应的后悔值却高于风险中性下的情况,即

通过比较Q*和Q*,以及ρ*和ρ*,可以容易得到定理3中的结论。同样,在有追索权的情况下,报童决策者的订货量和最优后悔值仅与、w、v、λ及区间[A,B]有关。特别地,当已知需求在[A,B]上服从均匀分布时,根据式,说明信息缺失情况下,当考虑追索权时,损失厌恶报童决策者仍可按照均匀分布进行决策,与风险中性情况下的结果一致。

推论5对于区间[A,B]上的任意非负累计分布函数F∈Ψ,损失厌恶报童的鲁棒订货量和对应的后悔值分别与损失厌恶系数λ呈负相关和正相关关系,即损失厌恶系数λ越大,损失厌恶报童决策者订货量越小,后悔值越大。

推论6对于区间[A,B]上的任意非负累计分布函数F∈Ψ,有如下结论成立:

(2) 对于初次订货单位成本w,存在阈值当时,损失厌恶报童的后悔值随初次订货单位成本w的增加而增加;当时,损失厌恶报童的后悔值随初次订货的单位成本w的增加而减小;当,损失厌恶报童的后悔值与初次订货单位成本w无关。

证明:根据式(15),有＜0,推论6(1)得证。根据式(16),有

推论6中的结论与风险中性情况下的推论1一致,即初次订货单位采购成本越高,期初订货量越小,原因在于追索权的存在使得决策者可以在实际需求发生时选择是否进行二次订货。当考察由于需求分布信息缺失而未能进行最优决策导致的后悔值与初次订货单位成本w的关系时,发现同样存在阈值当w低于该阈值时,决策者可以从与上游供应商的采购价格谈判中进一步获利;而当w高于该阈值时,初次采购价格越高反而越有利于下游报童决策者。

推论7对于区间[A,B]上的任意非负累计分布函数F∈Ψ,损失厌恶报童的鲁棒订货量和对应的后悔值均随二次订货成本的增加而增加。

推论8对于区间[A,B]上的任意非负累计分布函数F∈Ψ,损失厌恶报童的鲁棒订货量和对应的后悔值与剩余产品的单位残值v分别呈正相关和负相关关系,即剩余产品的单位残值越高,损失厌恶报童的订货量越大,后悔值越小。

推论9对于需求区间[A,B]上的任意非负累计分布函数F∈Ψ,当区间下界A固定时,损失厌恶报童的鲁棒订货量随着上界B的增大而增大;当区间上界B固定时,损失厌恶报童的鲁棒订货量随着下界A的增大而增大;当区间的上、下界均变化时,鲁棒订货量随区间范围的增大可能增加也可能减小。然而,损失厌恶报童的最优后悔值随区间范围的增大而增加。

推论9的证明同推论4,在此略去。推论9同样表明,虽然需求区间范围的大小与报童鲁棒订货量没有直接关系,但需求区间预测越精准,报童后悔值绩效越贴近最优情况。

4 数值算例及分析

为了更直观地展现文中给出的定理和推论中的相关结论,进一步对比分析风险中性和损失厌恶下的报童决策及运作绩效,针对文中所建模型及结果进行数值分析。不失一般性,假设需求上下界分别为A=20,B=200。

(1) 报童鲁棒订货量和后悔值与初次订货单位成本的关系

为了对比分析不同初次订货单位成本下,基于风险中性和损失厌恶的报童鲁棒订货量和后悔值绩效情况,相关参数设定如下:v=8,w^=11,λ=2.25,w∈[8,10]。根据定理1和定理2,得仅知需求区间信息条件下的报童鲁棒订货量和后悔值绩效随初次订货单位成本的变化情况如图3和图4所示。

由图3可以看出,无论是风险中性还是损失厌恶下,报童的订货量决策均随着初次订货成本的增加而降低。特别地,风险中性下的鲁棒订货量要高于损失厌恶下的情况。进一步,对比分析风险中性和损失厌恶下的报童后悔值绩效时,由图4可以看出,随着初次订货单位成本的增加,无论是风险中性还是损失厌恶报童的后悔值呈先增后减的变化趋势,与推论1和6的结果一致。当w=9.5时,风险中性下的报童后悔值达到最大值ρ*=135;当w=9.24时,损失厌恶下的报童后悔值达到最大值=194.26。这说明相对于损失厌恶情况,初次订货单位成本对风险中性报童决策者的阈值效应具有一定滞后性。由于风险中性下的报童订货量高于损失厌恶情况,因此,风险中性下对应的后悔值绩效要低于损失厌恶情况,与前文分析一致。

图3 报童鲁棒订货量和初次订货单位成本的关系Figure 3The relationship between robust order quantity and initial unit ordering cost

图4 报童后悔值与初次订货单位成本的关系Figure 4The relationship between regret value and initial unit ordering cost

(2) 报童鲁棒订货量和后悔值与二次订货单位成本的关系

为了分析风险中性和损失厌恶下,报童鲁棒订货量和后悔值绩效随二次订货单位成本的变化情况,相关参数设定如下:v=8,w=9,λ=2.25,w^∈[10,14]。根据定理1和定理2,得不同二次订货单位成本下,风险中性和损失厌恶报童订货量及对应后悔值分别如图5和图6所示。由图5和图6可以看出,随着二次订货单位成本的增加,风险中性和损失厌恶下报童鲁棒订货量和对应的后悔值绩效均呈递增趋势,特别地,为了规避可能带来的损失,损失厌恶下的订货量低于风险中性下的情况,从而导致对应的后悔值高于风险中性下的情况,与推论2和7中的结果一致。进一步,由图6可以看出,二次订货单位成本越高,损失厌恶和风险中性下的报童后悔值差距越大。这是由于对于报童决策者来说,一方面为了尽可能地满足不确定市场需求,希望供货商给予二次订货机会,另一方面又希望供货商给予较低的二次订货成本。因此,当二次订货成本较高时,损失厌恶态度和高昂二次订货成本对报童运作绩效的负面叠加效应使得损失厌恶下的后悔值明显高于风险中性下的情况。

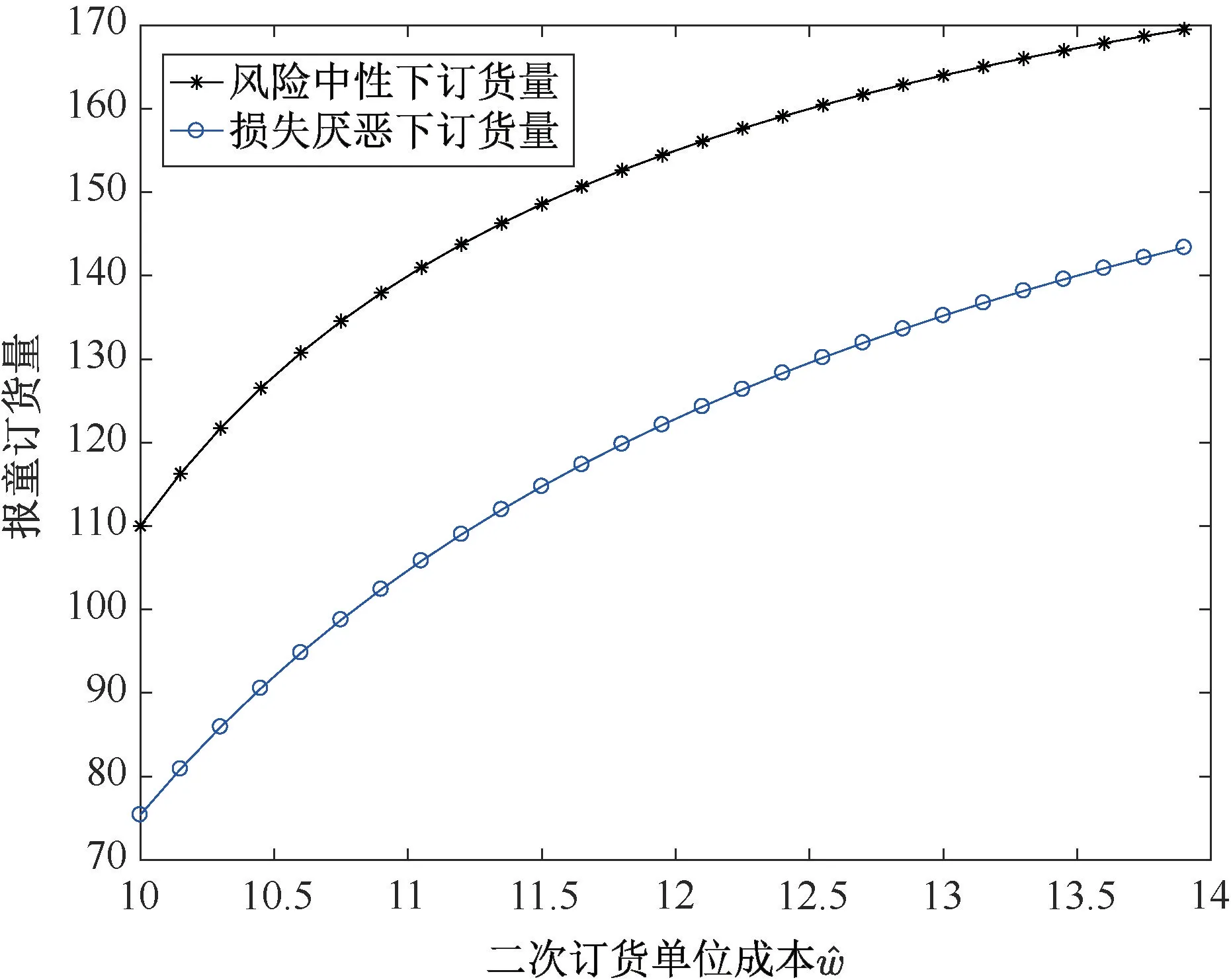
图5 报童鲁棒订货量与二次订货单位成本的关系Figure 5The relationship between robust order quantity and unit recourse cost

图6 报童后悔值与二次订货单位成本的关系Figure 6The relationship between regret value and unit recourse cost

(3) 报童订货量和后悔值与剩余产品单位残值的关系

为进一步分析风险中性和损失厌恶报童鲁棒订货量和对应的后悔值随剩余产品单位残值的变化情况,相关参数设定如下:10,w=9,λ=2.25,v∈[5,8]。根据定理1和定理2,得剩余产品不同单位残值下,风险中性和损失厌恶报童订货量及对应后悔值分别如图7和图8所示。由图7可以看出,无论是风险中性还是损失厌恶,报童鲁棒订货量均随着剩余产品单位残值的增加而增加。然后,随着剩余产品单位残值的增加,风险中性和损失厌恶下的报童后悔值却呈递减趋势,见图8,与推论3和8中的结果一致。同上,在不同的单位残值下,风险中性下的鲁棒订货量和对应的后悔值分别高于和低于损失厌恶下的情况。

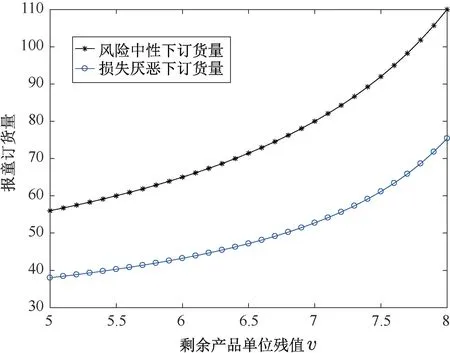
图7 报童鲁棒订货量与剩余产品单位残值的关系Figure 7The relationship between robust order quantity and unit salvage value

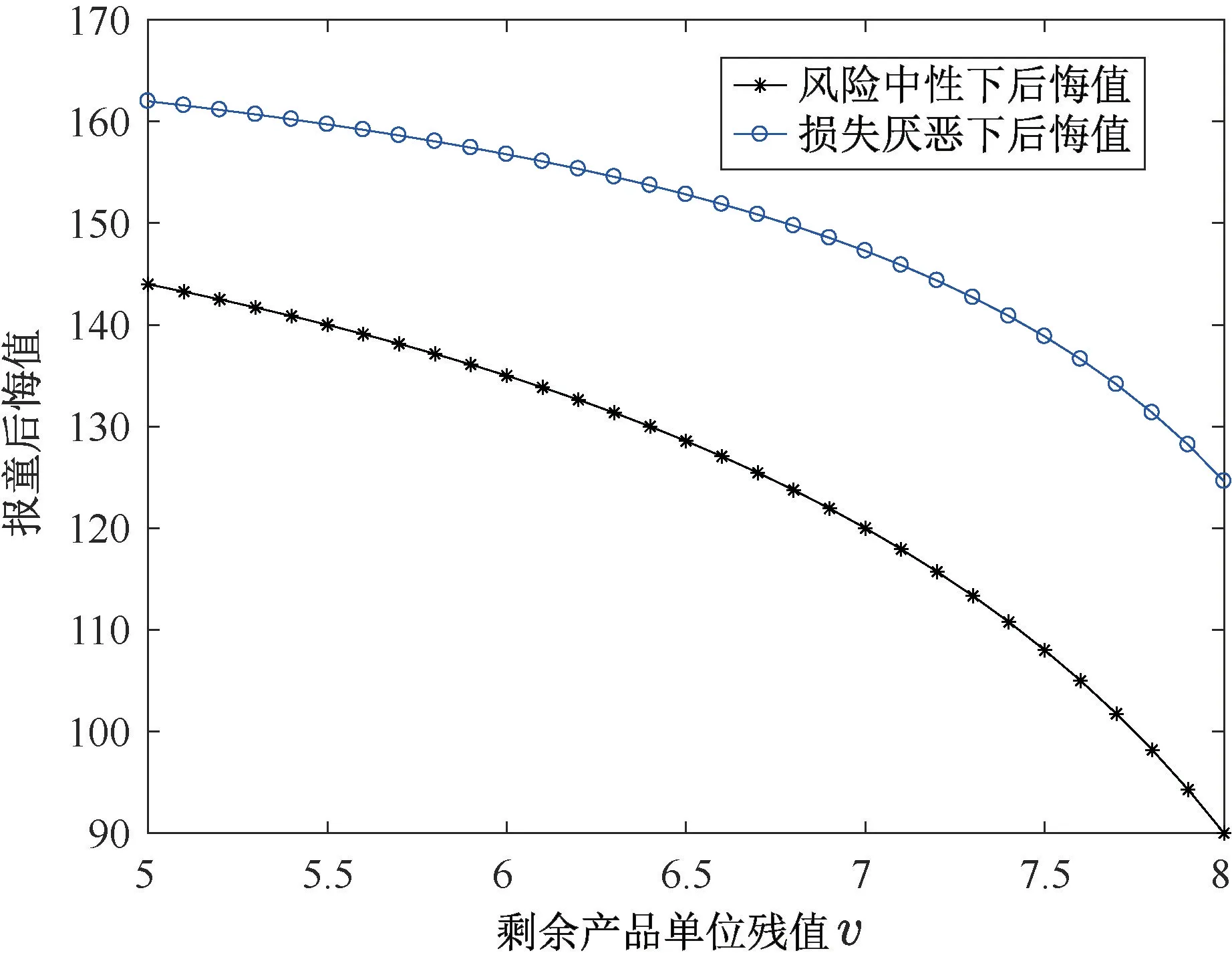
图8 报童后悔值与剩余产品单位残值的关系Figure 8The relationship between regret value and unit salvage value

(4) 损失厌恶报童鲁棒订货量和后悔值与损失厌恶系数的关系

根据前文报童期望效应函数,即式(14),λ＞1度量了决策者的损失厌恶态度。为了分析不同损失厌恶程度下的报童订货量决策和后悔值情况,相关参数设定如下:w^=10,w=9,v=8,λ∈[2,3]。根据定理2,得损失厌恶下报童鲁棒订货量和后悔值随λ的变化情况如图9和图10所示。由图9可以看出,随着参数λ的增加,鲁棒订货量呈递减趋势,这说明决策者损失厌恶程度越高,为了规避可能带来的损失,其期初订货量越低,对应地,报童后悔值越大,见图10,与推论5中的结果一致。

图9 损失厌恶报童订货量与损失厌恶系数的关系Figure 9The relationship between loss-averse newsboy′s order quantity and loss aversion coefficient

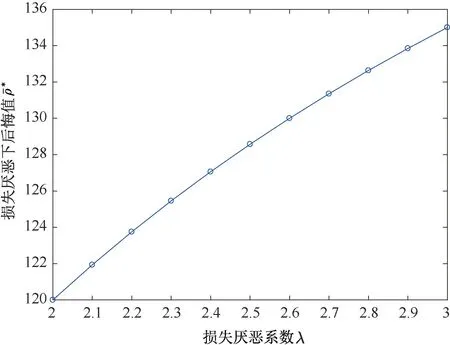
图10 损失厌恶报童后悔值与损失厌恶系数的关系Figure 10The relationship between loss-averse newsboy′s regret value and loss aversion coefficient

(5) 最小最大后悔值准则与其他决策准则的对比分析

现实中,在应用报童模型进行决策时,人们通常需要事先指定需求分布形式,例如,均匀分布、正态分布等。根据前文分析,γ=ρ(Q)/ρ*和分别度量了风险中性和损失厌恶下,其他决策准则和最小最大后悔值准则的优劣。当已知需求在区间[A,B]上服从均匀分布时,风险中性和损失厌恶下的报童订货量分别为:

根据定理1和定理2的证明过程,对于正态分布决策准则下的订货量,风险中性和损失厌恶下的最大后悔值分别为:

图11 风险中性下基于正态分布的报童后悔值与最小最大后悔值之比Figure 11The ratio of newsboy′s regret value to min-max regret value based on normal distribution under risk neutral

由图11和图12可以看出,当报童假设需求服从正态分布进行订货量决策时,无论是风险中性还是损失厌恶情况,均有成立,且该比值随相关参数的变化呈相同的变化趋势。特别地,最高比值为这说明基于正态分布的订货量决策将使得报童可能的利润损失高于文中最小最大后悔值准则下的利润损失,进一步验证了基于文中方法得到的订货量决策的鲁棒性。在报童模型中,尽管正态分布是管理者在随机需求下进行决策时被广泛采用的一种分布形式,但从后悔值分析角度,正态分布却具有较低鲁棒性。综合均匀分布和正态分布两种情况下的结果,可以得出如下结论:对于具有追索权的报童决策者,当仅知需求区间信息时,基于文中最小最大后悔值准则的订货量决策能够确保其较小的利润损失,具有良好的鲁棒性。特别地,从实际应用角度,无论是风险中性还是损失厌恶型报童决策者,均可通过事先假定需求服从均匀分布制定订货量决策。

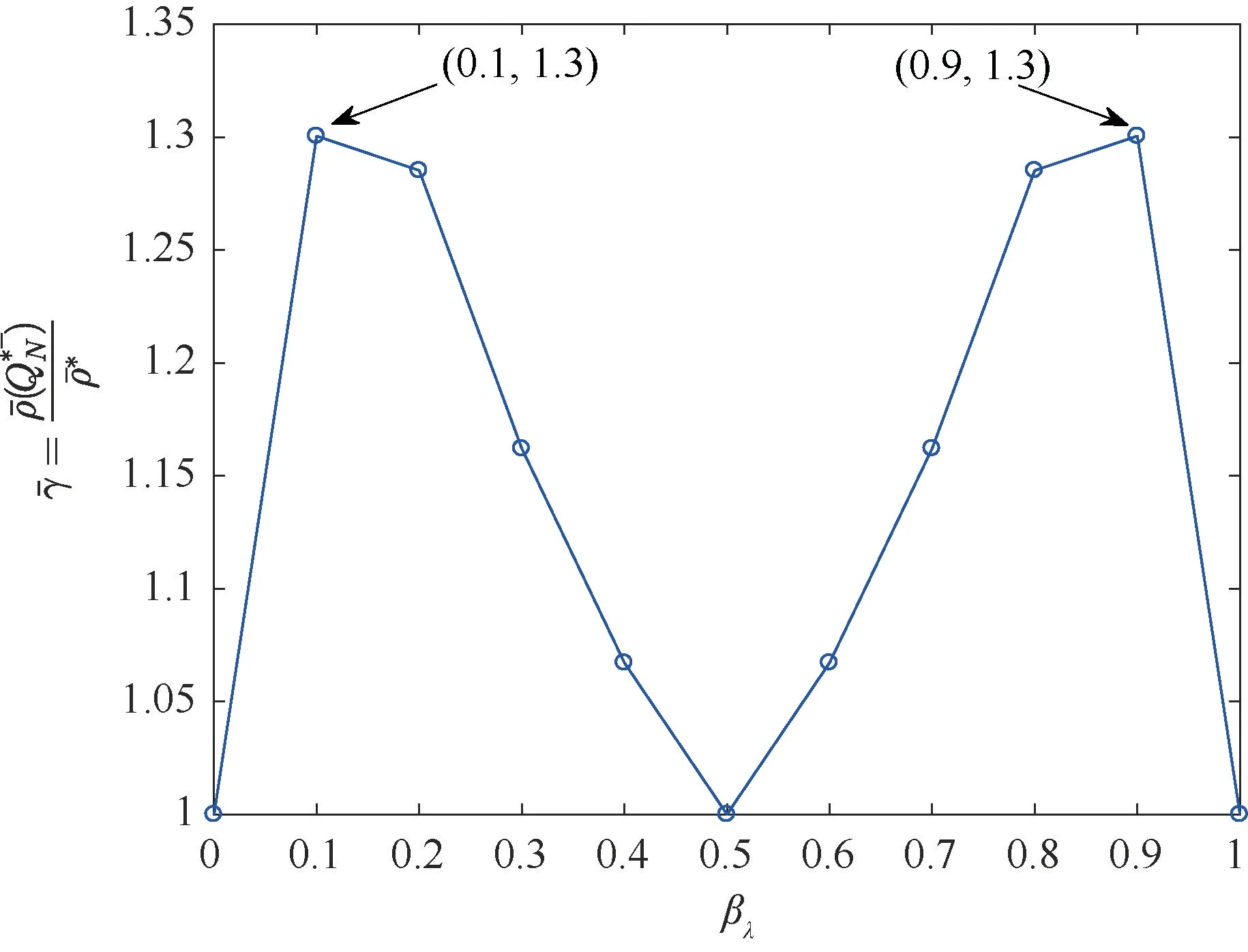
图12 损失厌恶下基于正态分布的报童后悔值与最小最大后悔值之比Figure 12The ratio of newsboy′s regret value to min-max regret value based on normal distribution under loss aversion

5 结论

本文针对有限需求分布信息下具有追索权的损失厌恶报童决策问题,建立了基于最小最大后悔值准则的报童鲁棒优化模型,给出了仅知需求区间条件下风险中性和损失厌恶报童决策者的鲁棒订货量及后悔值表达式,分析了损失厌恶系数、初次订货单位成本、二次订货单位成本、剩余产品单位残值以及区间范围等参数对报童鲁棒订货量和后悔值绩效的影响。基于本文研究结果,对从事报童类产品销售的企业提供如下决策建议:

(1) 当企业仅能估计市场需求的区间范围时,可基于需求服从均匀分布的假设进行订货量决策制定,因为该假设条件下得到的决策与基于较低保守性的最小最大后悔值准则得到的决策一致。从决策制定的难易程度考虑,均匀分布假设将更便于企业进行决策优化。此外,同风险中性情况相比,当决策者具有损失厌恶态度时,应减少期初订货量以规避库存过剩可能带来的损失。

(2) 当企业初次订货成本增加时,应减少期初订货量。然而,在允许二次订货的情况下,企业与上游供应商进行采购谈判时不能一味地压低采购价格。只有当供应商给予的初次采购价格低于某一临界值时,零售商进一步压低采购价格才能获利;而当供应商初次采购价格高于该临界值时,价格越高反而对零售商越有利。进一步,当上游供应商给予的二次订货价格较高时,企业应增加期初订货量以减少当需求超出期初订货量时导致的高昂的二次订货成本。

(3) 对于销售企业来说,由于较高的产品残值会显著改进其绩效,因此,决策者在日常经营过程中应提升其服务水平,通过提高附加于产品本身的服务价值确保产品在销售周期结束时具有较高的残值;考虑到较高的残值无论是对于消费者还是其下游零售商都具有较高的吸引力,为了提高产品残值,供应商应注重产品价值的提升,例如,通过技术创新改进产品功能、提升产品质量等。另一方面,无论是下游销售商还是上游供应商,提升产品价值的一系列举措又会反过来刺激市场需求的增加,从而使双方获利。

(4) 需求波动范围的增加会损害企业绩效,因此,决策者在日常经营过程中应注重数据的收集和预测方法的改进,提高需求隶属区间范围的精度,从而降低因难以掌握完备需求信息所带来的绩效损失。

本文仅研究了需求区间信息下考虑追索权的损失厌恶报童鲁棒优化问题,未来,可将问题扩展到包含上游供应商在内的二级供应链环境,采用博弈论方法研究考虑追索权和损失厌恶的供应链鲁棒运作策略,并进一步探讨供应链协调机制设计问题。此外,随着数据科学的发展,数据可得性问题在运作管理领域受到人们普遍关注。这种日益增加的数据可得性使得决策者可以从广泛的运作数据中尽可能多地挖掘决策信息,例如,除了需求区间信息外,可进一步获得需求均值或方差信息。基于此,研究多种信息条件下的报童鲁棒决策问题,并对比分析额外需求信息对于决策绩效的改进情况将是进一步研究方向。