可视化弹道的建模与仿真
2022-03-15张小石王宪升
张小石,王宪升,喻 翔
(重庆建设工业(集团)有限责任公司,重庆 400054)
0 引言
当今世界各国弹箭发展的总趋势是增大射程、提高命中精度和打击效果,因此出现了一大批已装备部队或正在研制的新型弹箭,它们既不是普通的无控弹,也不是一般意义上带有火箭发动机和全程制导的导弹,而是仍以普通火炮、火箭炮发射或飞机投放,通常不带动力,只在全弹道部分弧段上采取简易控制、弹道修正或目标敏感的智能化、信息化、制导化弹箭[1]。
对于无控弹箭的飞行仿真都是利用计算机进行,而对有控弹箭的外弹道仿真,为了更接近弹箭的实际有控飞行以及考察控制系统元器件的工作性能,可进一步利用转台代替弹箭的角运动并接入舵机、惯导、负载模拟装置、导航计算机、GPS模拟器、脉冲发动机等部分实物以及目标模拟器等进行半实物仿真,利用随动技术、相似原理和环境对实物进行测试和研究,以检验设计结果的正确性[2]。
在弹箭仿真过程中,利用可视化技术可以将弹箭飞行情况直观地表现在显示屏上,最快、最直观地了解弹箭在空中的运动姿态、质心轨迹。另外,通过参数的改变,还可以了解其对飞行的影响,进行参数优选,实现仿真数值信息实时地转化为虚拟环境下的三维图形图像信息,从而使得飞行仿真可视化系统更加逼真[3]。
1 弹道的建模过程
有控弹箭中,为了控制弹箭飞向目标,必须根据需要及时地改变速度方向和大小,这就需要提供垂直于速度方向(法向)的力和沿速度方向(切向)的力,以形成法向加速度和切向加速度。
产生法向力、改变速度方向的一个重要方法是形成必要的攻角α和侧滑角β,这需要弹箭绕质心转动改变弹轴方向(或称弹箭姿态)[4]。在有控弹箭上装有相对于弹身可以转动的面,称为舵面或操纵面,流经舵面的燃气或空气作用在舵面上的力对弹箭质心的力矩即形成操纵力矩,前者称为燃气舵,后者称为空气舵。在有控弹箭中由空气舵(或燃气舵)面转动产生空气动力或燃气动力形成对全弹质心的力矩——操纵力矩并通过它来实现改变弹轴方向或弹箭姿态[5]。
本文利用机械系统动力学分析软件ADAMS进行可视化弹道的仿真计算,在仿真过程中需要添加火箭弹阻力、升力、俯仰力矩和赤道阻力矩。
(1)火箭弹阻力由下式计算:
(1)
其中:ρ为空气密度;v为火箭弹飞行速度;Cx为阻力系数;S为火箭弹最大横截面积。
火箭弹阻力在ADAMS中的函数表达式为:
Rx=1.206 3/2*3.14/4*0.107*0.107*VM(cm)*VM(cm)*AKISPL(VM(cm)/340,0,SPLINE_1,0).
其中:AKISPL为驱动添加函数;SPLINE_1为样条曲线。火箭弹阻力添加示意图如图1所示。
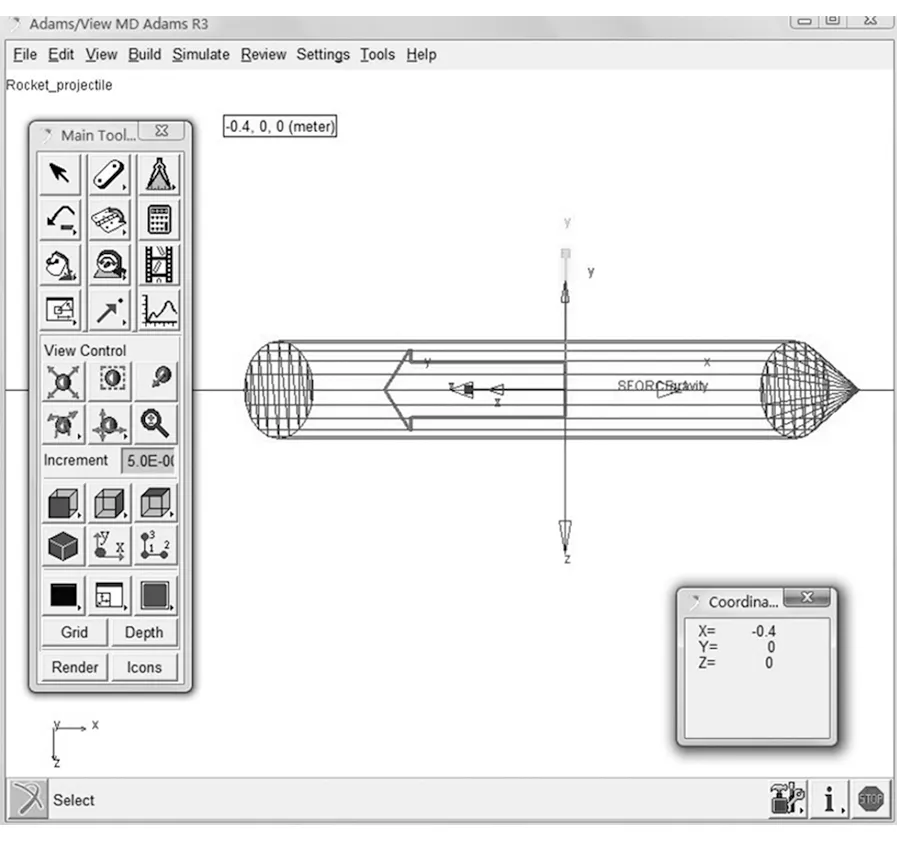
图1 火箭弹阻力添加示意图
(2)火箭弹升力由下式计算:
(2)

火箭弹升力在ADAMS中的函数表达式为:
Ry=1.206 3/2*3.14/4*0.107*0.107*VM(cm)*VM(cm)*AKISPL(VM(cm)/340,0,SPLINE_2,0)*ABS(ATAN(ABS((DY(MARKER_30,cm)/DX(MARKER_30,cm)))—ATAN(ABS(VY(cm)/VX(cm))))).
其中:ABS为绝对值函数;DY为Y轴距离测试函数;ATAN为正反切函数。
火箭弹升力添加示意图如图2所示。

图2 火箭弹升力添加示意图
(3)火箭弹俯仰力矩由下式计算:
(3)
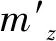
火箭弹俯仰力矩在ADAMS中的函数表达式为:
Mz=1.206 3/2*3.14/4*0.107*0.107*0.9*VM(cm)*VM(cm)*AKISPL(VM(cm)/340,0,SPLINE_3,0)*ABS(ATAN(ABS((DY(MARKER_30,cm)/DX(MARKER_30,cm)))—ATAN(ABS(VY(cm)/VX(cm))))).
火箭弹俯仰力矩添加示意图如图3所示。

图3 火箭弹俯仰力矩添加示意图
(4)赤道阻尼力矩由下式计算:
(4)

赤道阻尼力矩在ADAMS中的函数表达式为:
Mzz=1.206 3/2*3.14/4*0.107*0.107*0.9*0.9*VM(cm)*WY(cm)*ABS(ATAN(ABS((DY(MARKER_30,cm)/DX(MARKER_30,cm)))—ATAN(ABS(VY(cm)/VX(cm)))))*AKISPL(VM(cm)/340,0,SPLINE_4,0).
赤道阻尼力矩添加示意图如图4所示。

图4 赤道阻尼力矩添加示意图
2 弹道仿真与分析
2.1 无控弹道的仿真与分析
设火箭弹初始速度为40 m/s,初始转速为1 998 r/nim,即209.230 070 729 1 rad/s,在0.01 s~0.56 s火箭弹喷管推力和力矩作用下,使火箭弹速度和转速增大。设置仿真时间为50 s,仿真步数为10 000步,得到的仿真结果如图5~图11所示。

图8 火箭弹转速曲线 图9 火箭弹到达顶点时的速度 图10 火箭弹到达顶点时的转速
由图5~图11仿真结果可知,火箭弹弹道高为3.531 919 4 km,到达弹道顶点飞行时间为23.095 s;火箭弹飞行时间47.165 s,射程为10.908 587 9 km;在0.56 s时,即主动段末端,火箭弹速度达到最大值516.277 8 m/s,弹道终点时刻,火箭弹速度为344.349 4 m/s;在0.56 s时,即主动段末端,火箭弹转速达到最大值3 163.694 rad/s,即30 211 r/nim,弹道终点时刻,火箭弹转速为1 845.361 3 rad/s,即17 622 r/nim;火箭弹达到顶点时的速度为226.451 8 m/s,转速为2 393.715 4 rad/s,即22 858 r/nim,水平位移为6.147 250 1 km。

图11 火箭弹到达顶点时的水平位移 图12 控制力30 N作用下弹道的射程 图13 控制力40 N作用下弹道的射程
2.2 有控弹道的仿真与分析
将控制力分别设置为30 N、40 N和50 N,研究控制能力下弹道射程,结果如图12~图14所示,控制力与射程增加量的对应关系如表1所示。

表1 控制力与射程增加量的对应关系
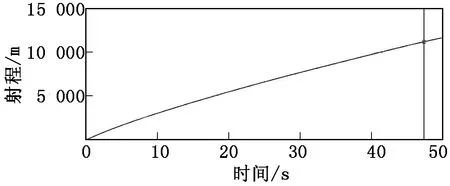
图14 控制力50 N作用下弹道的射程
3 结论
本文以某型火箭弹为例,借助MSC公司开发的机构系统动力学分析软件ADAMS进行可视化弹道的建模与仿真。
(1)通过ADAMS软件,可直观、形象地观察火箭弹飞行姿态和轨迹,并能在显示动画的同时显示曲线的数据位置,从而观察运动与参数变化的对应关系。
(2)研究了基于脉冲力和气动舵机进行控制的有控弹道的性能,得到了控制力作用时弹道的射程,进而研究其控制能力。
通过可视化弹道的建模与仿真,看到可视化技术在弹道仿真计算方面较传统弹道计算的优势所在,为今后研究弹道提供了一个很好的方法。
