弓形卸扣本体受力计算公式探讨

姜明远，王宝中，林风梅

(1.华北理工大学 机械工程学院，河北 唐山 063009；2.巨力索具股份有限公司，河北 保定 071000)

0 引言

卸扣是吊索具的一种，在中国是一个十分有发展前景的产品。卸扣的应用范围非常广泛，适用于各个工业制造、大型吊装和工程建设领域。早期，由于国内对卸扣的材料和结构研究不够深入，缺乏在安全设计系数下的可靠设计方法，只能依靠国外的样本进行模仿制造[1]。现如今，对卸扣的研究更近一步，蔡裕民在《吊装工艺计算近似公式及应用》中提出了计算D形卸扣最大应力的公式。弓形卸扣比D形卸扣具有更强的承载力和更精美的外观，应用更为广泛。由于弓形卸扣受力情况较为复杂，所以现在还没有针对弓形卸扣最大应力的计算公式。本文探讨同样额定载荷下D形卸扣的计算公式可否用于或在什么样的条件下可以用于弓形卸扣最大应力计算，以巨力索具公司额定载荷为9.5 t的弓形卸扣为例，通过用ANSYS Workbench进行有限元分析的方法来模拟受力情况，对比仿真结果和计算结果，为得到弓形卸扣本体最大应力的计算公式提供理论依据。

1 产品基本信息

巨力索具公司额定载荷为9.5 t的弓形卸扣如图1所示,其吊环螺钉和销轴是螺纹联接，即将吊环螺钉拧入销轴中。

图1 巨力索具公司额定载荷9.5 t的弓形卸扣

该弓形卸扣的重量为4.25 kg，额定载荷为9.5 t，卸扣本体和销轴采用的材料为34CrNiMo6，其屈服应力σs≥760 MPa、抗拉极限σb≥1 075.2 MPa。卸扣本体和销轴所用材料属于合金钢类材料，分析设定材料信息时取相同的参数，合金钢的性能参数为：密度7 850 kg/m3，弹性模量206 GPa，泊松比0.3。

2 有限元分析计算

2.1 有限元模型的建立

选用ANSYS Workbench软件中的static structural模块进行有限元分析[2]。通过三维建模软件SolidWorks对此卸扣进行建模，由于在实际工况中吊环螺钉、R形开口销在吊装过程中不受力，所以分析时将其抑制，在后面的分析中不对其进行分析，从而简化模型，减少运算过程的计算量，提高仿真模拟准确性。该卸扣用于吊装作业，卸扣本体上端与20 t高强度环形吊带连接，吊带厚度约38 mm、宽度约70 mm，通过static structural模块中的Design Modeler在卸扣本体上端分割一个宽度为70 mm的表面，在这个表面上施加竖直向上的力来代替卸扣本体上端与20 t高强度环形吊带连接的受力。卸扣的销轴与Crosby公司的M24×36吊环螺钉相连，将吊环螺钉的底部设为固定面[3]。卸扣受力面如图2所示，卸扣固定面如图3所示。

图2 卸扣受力面

图3 卸扣固定面

2.2 定义接触类型

在Model环境中定义卸扣的接触类型。根据实际的工况，卸扣的接触类型设置如表1所示。表1中，Bonded为绑定接触，No Separation为不分离接触。

表1 卸扣的接触类型设置

2.3 划分网格

根据产品外形特点，在ANSYS Workbench中选取四面体网格中的Patch Independent方法来对卸扣本体和销轴进行网格划分，这种网格划分方法能很好地划分连接面之间的过渡区域，得到较好的网格划分结果[4]。由于吊环螺钉不是这个仿真分析的主要部件，故将吊环螺钉用自动划分网格的方式来划分网格。划分质量较好的网格可以满足后续的分析需求，网格划分质量报告如图4所示。图4中，横坐标表示的是网格度量。网格度量以1为最大，越接近1说明网格质量越好。

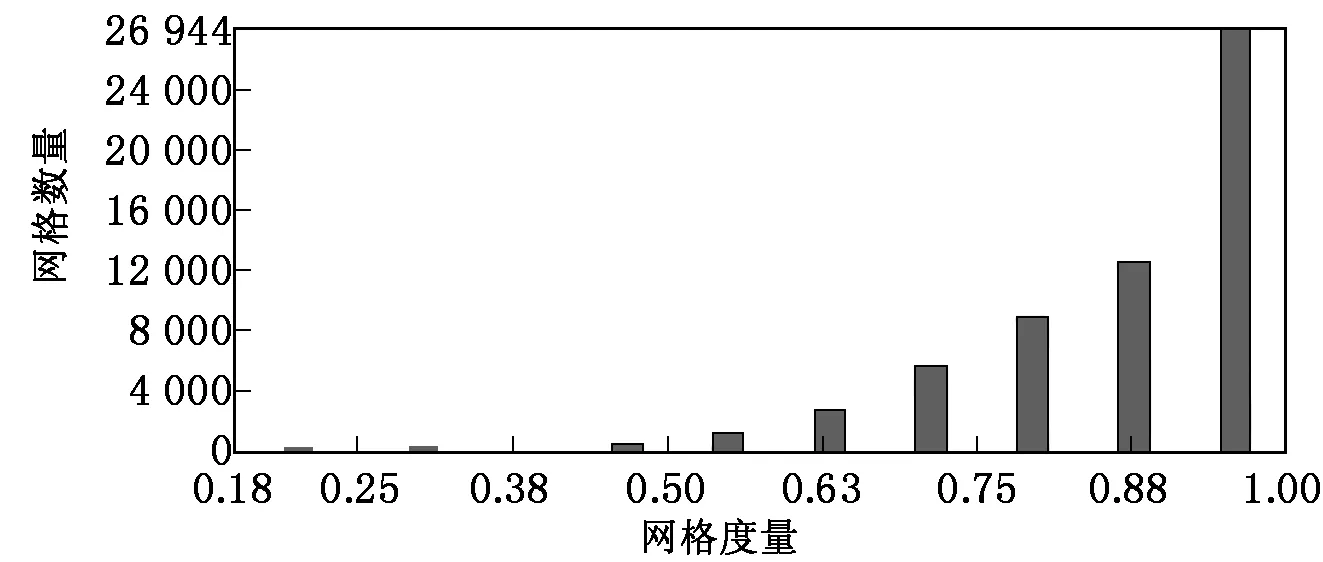
图4 网格质量

3 受力模拟分析

在卸扣受力面上分别施加2.5 t、5 t、7.5 t、9.5 t、12.5 t、15.5 t、18 t、19 t、23 t、27 t、31 t、35 t、38 t、40 t的载荷，得到卸扣本体最大应力数值，如表2所示。

以施加载荷9.5 t为例进行说明，9.5 t载荷相当于93 100 N的力，在Workbench软件中输入力93 100 N，得到如图5所示的应力云图[5]。

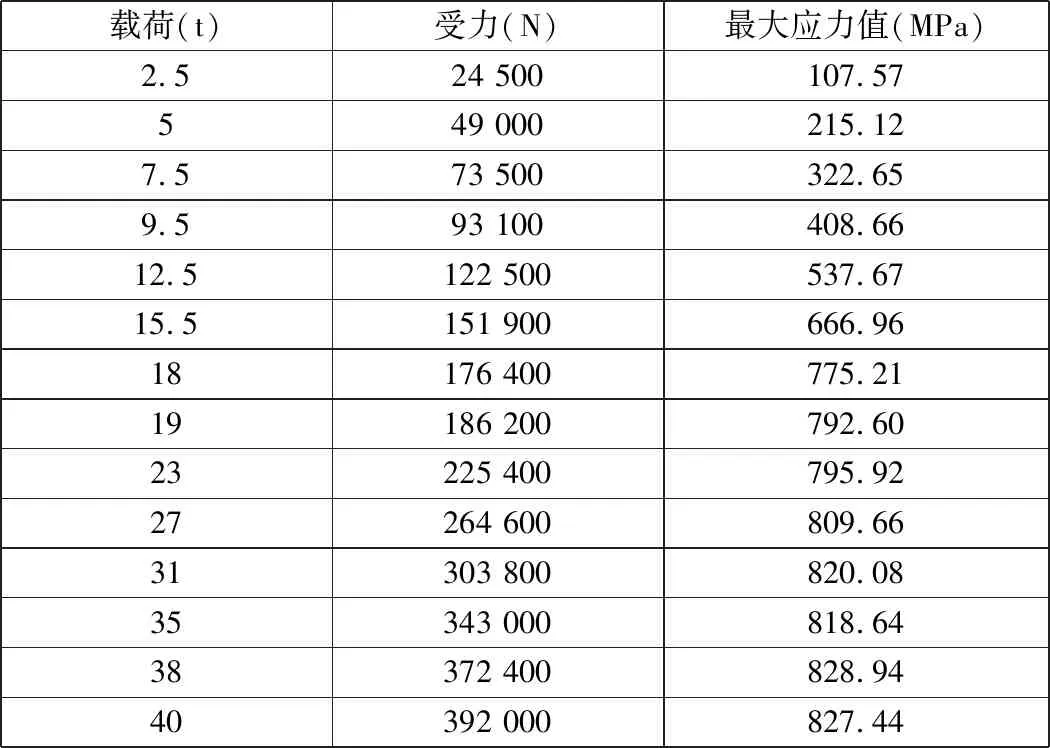
表2 仿真分析得到的卸扣最大应力

图5 施加载荷9.5 t时卸扣本体最大应力云图

从图5中可知，当受力面上施加93 100 N的力时，卸扣本体最大应力为408.66 MPa。

4 公式计算

图6为D型卸扣尺寸图。《吊装工艺计算近似公式及应用》中对D型卸扣本体的应力公式推导为：将卸扣本体视为链环的一半，按曲梁弯曲公式计算，并考虑“强化系数”，则环曲线部分中点的应力计算公式为[6]：

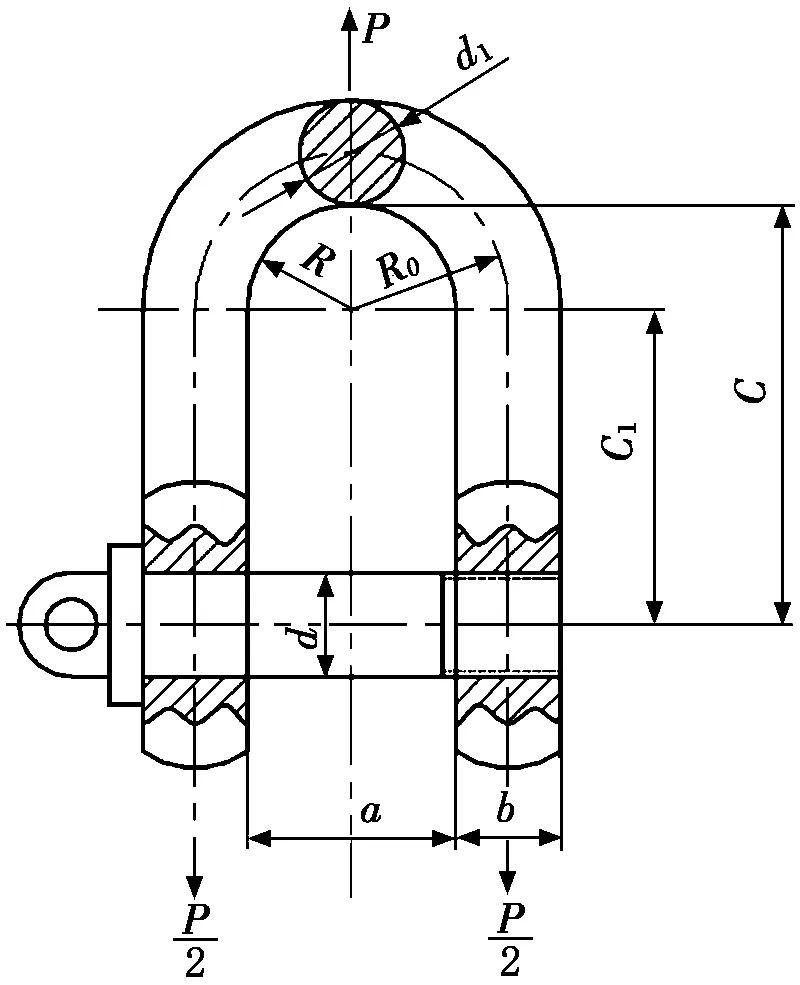
图6 D形卸扣尺寸图

(1)

(2)

本文以巨力索具公司额定载荷为9.5 t的弓形卸扣为例进行计算，图7为该弓形卸扣本体的具体尺寸图。

图7 弓形卸扣尺寸图

将其余的载荷分别进行计算，结果如表3所示。

表3 公式计算得到的弓型卸扣最大应力汇总

5 结果对比与分析

不同受力情况下仿真和公式计算得到的弓形卸扣的最大应力数值汇总如表4所示。

将表4中数据转换成折线图可以更加清晰直观地显示两组数据的相同和差异，卸扣本体最大应力数值对比，如图8所示。

表4 仿真和公式计算得到的弓型卸扣最大应力汇总

由图8可以看出：公式计算得到的卸扣本体的最大应力和有限元分析得到的卸扣本体最大应力在卸扣本体受力186 200 N之前结果相似，有限元分析得到的结果略大一些，两者最大误差约为8.1%；在受力186 200 N之后差别较大。分析原因为卸扣本体所用材料为34CrNiMo6，其屈服强度为760 MPa，当卸扣本体受力大于186 200 N的时候，卸扣本体发生塑形变形，此时材料进入屈服阶段，当受力逐渐加大时，其应力变化较为平缓，但是对于公式来说，公式内没有考虑材料的影响因素，所以在图8中卸扣本体最大应力总体呈现线性上升的趋势，没有因为材料到达屈服强度而变化。

图8 卸扣本体最大应力数值对比图

6 结论

通过对计算结果和有限元分析结果对比分析可以得到结论：当卸扣本体最大应力小于制造卸扣材料的屈服强度的时候，蔡裕民在《吊装工艺计算近似公式及应用》中提出的计算D形卸扣最大应力的计算公式也可以用来计算相同额定载荷的弓形卸扣本体的最大应力值。这个结论可以用于弓形卸扣的设计计算和对不明吨位的弓形卸扣进行核算，以此来满足相关的工程吊装要求。