用自由效用模型刻画出行选择行为

王 浩，闫小勇

（北京交通大学，a.综合交通运输大数据应用技术交通运输行业重点实验室，b.交通系统科学与工程研究院，北京 100044）

0 引 言

出行是人们生活中不可缺少的环节[1]。每次有潜在的出行需求时，人们都会考虑是否出行、去往何地、何时出发、使用何种交通方式和选择什么路径[2]。出行者们的这些出行选择行为是复杂交通流动现象的重要成因。刻画群体出行选择行为来预测出行需求是交通科学中的一个重要研究领域，也是交通规划工作中的一个重要环节[3,4]。传统的出行需求预测方法包含出行生成、出行分布、方式划分和交通分配四个阶段[5]。尽管每个阶段中都包含了大量的备选模型，但这些模型背后的建模机理是不同的。例如，预测出行生成多使用线性回归模型，预测出行分布多使用类比牛顿引力定律的重力模型[6]，预测方式分担率多使用计算个体选择各选项概率的Logit 模型[7]，分配交通流量则多使用考虑出行者相互作用的路径选择博弈模型，即用户平衡（User Equilibrium, UE）模型[8]。事实上，出行者选择是否出行、出行时间、目的地、方式和路径都是人的选择行为，背后应该有一致的普适性规律。但目前能统一刻画相互作用群体出行选择行为的建模框架依然缺乏[9]。

在交通科学领域，研究者很早就开始使用以Logit模型为代表的基于随机效用理论建立的离散选择模型来进行不同阶段的出行需求预测[7,10]。但这类模型大多是从个体选择行为角度建立的，并未考虑实际交通系统中普遍存在的个体之间的相互作用。而实际中的出行者不管是选择目的地和出行方式，还是选择出发时间和路径，都会考虑与其他出行者相互作用所导致的拥挤或拥堵问题。另一类可同时进行多阶段出行需求预测的模型是组合模型[11,12]，例如Yao 等建立的包含出行分布和交通分配的组合模型[2]；Boyce 等建立的考虑出行者目的地、方式和路径选择的组合模型[13]；Ali Safwat 和Magnanti 建立的出行生成、出行分布、方式划分和交通分配四阶段组合模型[14]等。这方面的研究大多是将多阶段出行组合预测问题转换为扩展网络上的交通分配问题，再用UE 模型等进行流量分配[11,15]。UE 模型考虑了路段拥堵问题，但UE模型的目标函数为何是网络路段成本函数的积分之和，一直缺乏合理的解释[15,16]。最近，Wang 等建立了一种存在相互作用的出行者们选择目的地的自由效用模型[17]，这一模型不仅能解释广泛存在于各类复杂社会系统中的引力定律，也为建立刻画群体出行选择行为的统一框架提供了新的途径。

在本文中，将自由效用模型扩展到出行需求预测的多个阶段。首先，用最简单的自由效用模型来刻画出行者选择出行方式的行为，该模型反映了出行者对期望效用与信息处理成本之间的权衡以及出行者之间的相互作用。然后，用自由效用模型来刻画出行者的目的地选择行为，并由此导出单约束重力模型和双约束重力模型。进一步地，用自由效用模型来刻画出行者在交通网络上的路径选择行为。最后，建立一个组合的自由效用模型来同时刻画出行者的目的地、方式和路径选择行为。用能反映个体间相互作用的自由效用模型刻画出行选择行为，不仅可以让我们从人类选择行为的角度更好地理解多种出行需求经典模型背后的根源，还为出行需求预测提供了一个更具可解释性的统一建模框架。

1 出行方式选择

式中：L是拉格朗日函数；λ是拉格朗日乘子。

由于对所有交通方式都有∂L/∂pk= 0，可以得到：

这意味着在出行者的最优选择策略下，所有出行方式的效用减去边际信息处理成本都相等。这种情况与微观经济学中的消费者均衡[25]中每种商品的边际效用都相等的情况非常类似。因此，将uk-τ( lnpk+ 1)命名为出行方式k的边际效用。相应地，由于微观经济学中消费者的总效用是所有商品边际效用的积分之和[25]，那么这个简单交通系统的总效用就是所有出行方式边际效用的积分之和。出行者的最优选择策略是遵循等边际准则[25]来选择出行方式，以使总效用最大化。结合式(3)和∑kpk= 1，可以得到式(1)的平衡解：

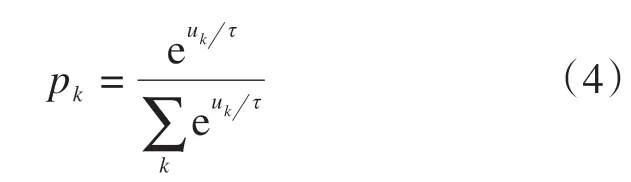
如果参数τ= 0，意味着信息处理不需要成本，该出行者会选择效用最高的出行方式。如果τ→∞，意味着信息处理成本非常高，该出行者将不考虑预期效用而只关注信息处理成本，在这种情况下，该出行者会完全随机地选择出行方式。式(4)与根据随机效用理论导出的Logit模型[7]在数学形式上是一致的，但推导不需要事先假设出行者对方式效用的感知误差服从独立同分布的Gumbel分布。

进一步地，将交通系统扩展到具有无穷多个(即T≫1)出行者的情形，这些出行者的属性都相同，每个出行者只有一次出行，那么问题就变成了这些出行是如何在各种出行方式上分布的。在实际中，出行方式k的效用会受到使用相同方式的出行者数量Tk的影响，即uk是Tk的函数，例如，公共汽车上乘客人数的增加将降低公共汽车乘客的舒适度。因此，效用可以被写为uk(Tk)，这是一个单调递减可微的函数。前已述及出行者会遵循等边际准则做出最优的选择，在这种情况下，任何一个出行者对出行方式的选择都依赖于其他出行者如何在各种出行方式上分布[26]。这种在社会系统中普遍存在的一个人的行为依赖于其他人行为的现象被称为个体交互。在此交互系统中，出行者们的最优选择策略是让所有出行方式都具有相同的边际效用。由于系统的总效用是所有出行方式边际效用的积分之和，因此交互系统的效用最大化模型可以写为：

式(5)的目标函数与物理学中的亥姆霍兹自由能函数[28]在数学形式上是一致的。因此，式(5)被命名为自由效用模型[17]。换句话说，这个出行方式选择系统可以类比为一个包含若干子系统、与热库进行热接触的等温等容热力学系统：出行者的数量类比为粒子的数量；式(5)目标函数的第一项类比为包含势能的热力学系统的内能（因此在势博弈中此项被命名为势函数[27]）；信息处理价格类比为热库的温度；信息熵类比为热力学系统的熵；信息处理成本类比为热力学系统与热库之间交换的热量；出行方式的边际效用类比为子系统的化学势。然而这两个系统的本质是不同的：热力学系统遵循自由能最低原理使系统达到平衡状态，在该状态下所有子系统均具有相同的化学势[28]；而出行方式选择系统自由效用的最大化则是出行者遵循等边际准则做出的最佳选择策略所导致的结果。

2 出行目的地选择

根据实际数据设置合适的效用函数uij(Tij)后，式(6)中的自由效用模型就可以直接用于出行分布预测。此外，在实际出行分布预测工作中被广泛使用的重力模型也可由自由效用模型导出。为导出重力模型，自由效用模型的效用函数需要与从i到j的出行量具有对数关系，即uij(Tij)=Aj-cij-γlnTij，其中Aj是目的地j的固定吸引力，反映了地点的活动机会（例如零售活动、就业密度等）[11]，cij是从i到j的固定出行成本，γlnTij是出行拥堵成本函数，γ是非负参数。此时式(6)可以被具体化为：

3 出行路径选择

从式(11)中可以看出，交通网络上的自由效用模型在数学形式上与交通科学中用于交通流分配的随机用户平衡（Stochastic User Equilibrium,SUE）模型[33]是一致的。有许多算法可以求解此模型并计算网络中所有路段上的流量[11]。在信息处理价格为0（即τ= 0）的情况下，式(11)中的自由效用模型在数学形式上与经典的UE 模型[8]一致。UE 模型的平衡解（即每对起终点之间所有被使用的路径都具有相等且最小的成本）就是出行者遵循等边际准则做出的最优路径选择策略的结果。UE 模型的目标函数（即每条路段边际效用积分之和的负值）实际上是没有信息处理成本的负自由效用。这为理解交通科学中的UE 和SUE 模型提供了一个新视角。

4 组合模型

截至目前，已经用自由效用模型分别刻画了出行者的方式选择、目的地选择和路径选择行为。但实际中的出行者不是分阶段选择这些选项的，而是会同时考虑去往何地、使用什么交通方式和选择哪条路径。因此，还应该在自由效用模型框架下对这些出行选择行为进行组合建模。

在本文中，用一种网络扩展方法来同步求解出行方式、目的地和路径选择问题。网络扩展的示意图见图1，图中最下层表示实际的多方式交通网络，其中标记为i的圆点表示交通小区的形心，它能产生和吸引出行量；方点表示交通网络中的普通节点，例如交叉口或地铁站；节点之间标记为a的有向连边表示路段，其中实线表示道路路段，点划线表示地铁线路。每条连边都有一个效用函数ua(xa)来表达连边效用ua和流量xa之间的关系。通过添加两类虚拟节点和两类虚拟连边来扩展这个实际交通网络。首先，给每一个节点i都添加一个虚拟目的地节点i′（见图1 中间层的圆点），并在两者之间添加一条虚拟连边ii′（见图1 最下层圆点与中间层圆点之间的虚线）。连边ii′上的流量是xii′，反映了实际目的地i的出行吸引量。连边ii′的效用函数是负的目的地可变吸引力函数-lii′(xii′)，它表达了实际目的地i的拥挤成本lii′与其出行吸引量xii′之间的关系。然后，再给每一个节点i添加一个虚拟起点i″（见图1 最上层的圆点），并在虚拟目的地i′与除与其编号对应的虚拟起点i″之外的其他所有虚拟起点之间添加一条虚拟连边i′i″（见图1 中间层圆点与最上层圆点之间的点线）。连边i′i″上的流量是xi′i″，反映了起终点之间的出行量，连边i′i″的效用函数是目的地i′固定的吸引力Ai′。通过以上方法就可以得到扩展后的网络。

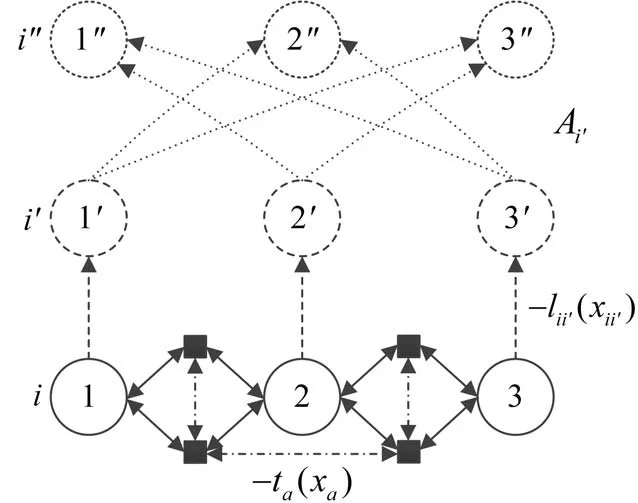
图1 网络扩展示意图

在这个扩展网络上，从起点i到虚拟起点i″的固定出行量是Oi，即i点的出行发生量。因而，出行方式、目的地和路径选择组合问题就转化为了在这个扩展网络上的路径选择问题。这个拓展网络上的自由效用模型为：

为更好地说明上述组合模型，在此增加一个算例。建立了一个简单的扩展网络，见图2（a）。其中最下层的圆点是3 个小区，1、2、3 小区的出行发生量分别为O1= 600、O2= 690、O3= 1000。最下层两条实线连边表示道路路段，两条点划线连边表示地铁线路，它们的效用函数分别为u12= -20 -x12、u23= -20 -x23、u32= -10 -2x32、u21= -10 -2x21，其中x表示连边上的流量，下同。最下层小区和中间层虚拟目的地之间3 条虚拟连边的效用函数分别为u11′= -x11′、u22'= -x22'、u33'= -x33'。中间层虚拟目的地到最上层虚拟起点之间6 条虚拟连边的效用函数分别u1′2″=u1′3″= 600、u2′1″=u2′3″= 100、u3′1″=u3′2″= 1000。为计算简便，此处假设信息处理价格τ= 0。将3 个小区的出行发生量看作是从最下层节点到最上层节点的出行分布量T11″= 600、T22″= 690、T33″= 1000，就可以用求解UE 模型的算法求得该算例的最优解，见图2（b）。最优解中的路段流量分别为x21= 470、x12= 600、x23= 900、x32= 1000，3 小区的实际出行吸引量分别为D1=x11′= 470、D2=x22′= 920、D3=x33′=900，小区之间的实际出行分布量分别为T12=x2′1″= 255、T13=x3′1″= 345、T21=x1′2″= 135、T23=x3′2″= 555、T31=x1′3″= 335、T32=x2′3″= 665。最下层节点到最上层节点之间6 条路径的边际效用见表1。

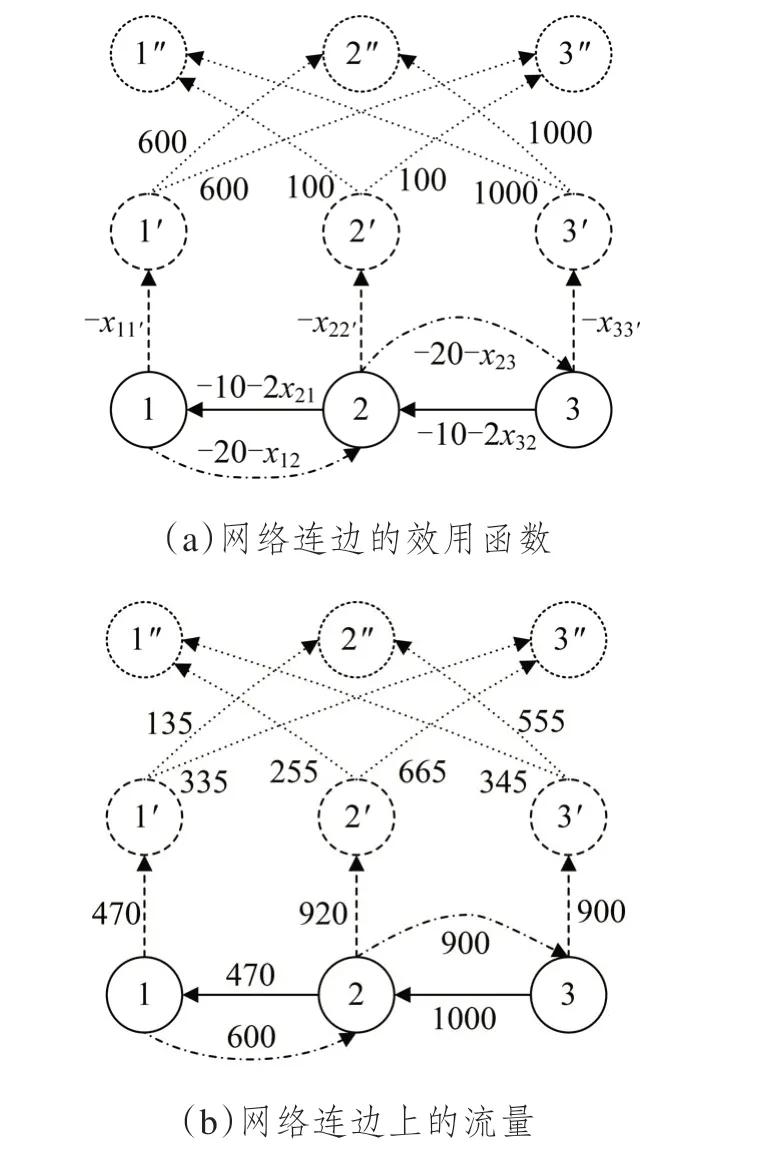
图2 组合模型算例网络

表1 小区之间路径的边际效用

5 结束语

本文用自由效用模型分别刻画了出行者们的出行方式、目的地和路径选择行为。自由效用模型有两个基本假设[17]，即个体追求效用最大化，且个体为了掌握更多关于选项效用的知识需要付出信息处理成本。与出行需求预测四阶段法中的多数模型相比，自由效用模型可以更好地刻画出行选择行为。例如，预测方式分担率的Logit 模型[7]、预测出行分布量的最大熵模型[31]和自由成本模型[30]都没有反映出行者之间的交互；传统的UE[8]和SUE 模型[33]虽然数学形式上与描述路径选择的自由效用模型一致，但它们目标函数中路段成本函数的积分项却一直缺乏合理的解释。而自由效用模型能同时反映个体在期望效用与信息处理成本之间的权衡和个体之间的相互作用，不仅可以从人类选择行为的角度更好地理解前述出行需求经典模型背后的根源，还可以在一个更具可解释性的理论框架下研究出行者的决策制定过程。

进一步用自由效用模型建立了同时考虑出行方式、目的地和路径选择行为的组合模型。相对于传统的出行需求预测四阶段法，组合多个阶段的模型更符合实际出行者的选择行为。尽管本文中只组合了出行方式、目的地和路径三类选择行为，在自由效用模型框架下还可以加入其他出行选择行为。例如，在图1 中为每个起点i和它对应的虚拟起点i″之间添加一条弹性需求连线并为其设置合适的效用函数，就可以在给定潜在的最大出行发生量的前提下，预测起点i实际的出行发生量。此外，在多状态超级交通网络中[34,35]，还可以用自由效用模型对出发时间选择行为[36]和其他出行选择行为进行组合建模。不仅如此，还可以通过收入水平、是否拥有私家车、是否通勤等因素对组合模型中的出行者进行分类，让组合模型更符合实际。总之，在更具可解释性的自由效用框架下建立的组合模型能更系统地研究出行者的完整出行决策制定过程。特别是在当前这个能反映人类移动的大数据时代，通过从这些大数据中挖掘群体出行选择规律来合理设置自由效用模型中的各类效用函数，可以为精确定量分析处处充满着出行者相互作用的复杂交通系统提供更多可选的工具。

尽管在本文中是用自由效用模型刻画交通系统中的出行选择行为，这一模型还可以应用到很多存在选项选择行为的社会系统中。从式(5)中可以看到，自由效用模型在数学形式上与随机势博弈模型[37]是一致的，还可以退化为经典的势博弈模型[27]，这类势博弈模型已被广泛应用于许多社会系统中的群体选项选择问题上。势博弈模型中的目标函数是类比物理学中的势函数建立的。势博弈中的一个玩家变动自己选项所导致的自身收益变化量与势函数变化量是相等的。势博弈的平衡解就是势函数最大时的解，此时所有玩家具有相同的收益，玩家不能单方面改变选择策略来提高自身的收益。但是，Monderer 和Shapley 对如何解释势函数提出了一个问题：玩家们试图共同实现什么最大化[27]？实际上，势函数不是玩家们共同追求的目标。现在从自由效用模型中已经知道，玩家只会最大化他们自己的效用（即收益），采用的最佳策略就是让自己所有选项的边际效用都相等。当所有玩家都遵循这样的等边际准则时，各个选项边际效用积分的和（在经济学中被称为总效用）自然就是最大的。换句话说，势函数最大是玩家个体最优选择策略的结果，而不是玩家们共同追求的目标。这对势博弈模型有了更本质的理解，能更好地为各类复杂社会系统中的选择行为建模。总之，自由效用模型不仅有助于深入理解交通系统中的出行选择行为，在预测、引导甚至控制各类复杂社会系统中的人类选择行为也具有潜在的应用价值。