基于系统动力学的连锁超市多级库存优化研究
2022-03-15谭慧敏闫星臣郑竞恒
□ 谭慧敏,白 桦,闫星臣,郑竞恒
(1.南京林业大学 汽车与交通工程学院,江苏 南京 210037;2.华设设计集团,江苏 南京 210000;3.苏州市运输管理处,江苏 苏州 215000)
自2004年年底中国零售业开始向外资全面开放[1],大量外资超市涌入国内市场,我国连锁超市迎来了前所未有的激烈竞争,本土连锁超市得到飞速发展的同时也显现出了诸多问题。突出表现在库存管理方面,主要有:①供应商众多,未形成统一配送。有些商品供应商自行配送至超市门店,给店员带来一定的工作压力且运输效率不高;②库存管理系统信息化程度不高。门店方只负责记录店面库存和预测未来需求,不与供应商形成统一的联网库存管理体系;③供应链上各节点库存各自为政,库存信息共享水平较低。供应商和连锁门店单独管理各自库存。
现代管理体系中,库存是保证连锁超市高效率运营和利润最大化的关键因素[2]。因此,库存优化对提高连锁超市核心竞争力具有重要意义。连锁超市库存优化涉及供应商、配送中心和超市等多类实体,是供应链多级库存管理问题,在该问题中,单纯强调单一节点的库存问题,需求的不真实性会从供应链底部开始逆向传播,产生需求逐级放大的牛鞭效应问题[3]。对于连锁超市多级库存系统的动态复杂性以及由此产生的牛鞭效应问题,系统动力学是一种流行且有效的研究方法。汪小京等将第三方物流引入供应商管理库存模式中,建立了VMI-APIOBPCS系统动力学模型,测试在不同的需求状态下模拟系统的表现[4]。李卓群建立闭环供应链系统动力学模型,分析缺货策略下回收物流的牛鞭效应[5]。黄杰等以制造企业为背景,建立包括两个供应商和一个制造商的供应商库存管理动态仿真模型[6]。这些文献仅着眼于供应链的局部问题进行研究,但关于系统动力学应用于处理连锁超市多级库存管理中的问题的文献还是比较少的。本文利用系统动力学定量和定性分析结合的特性建立了包括供应商-配送中心-超市门店的连锁超市库存系统动力学模型,以案例分析的形式,借助Vensim平台对模型进行仿真模拟,运行并修正相关参数,最终得出优化结果和对超市实际运营提供改进措施。
1 基于系统动力学连锁超市库存系统模型的构建
系统动力学模型是一种动态的仿真模型,它可以表达在不同的条件下和不同的时间状态下整个系统的动态变化。本文通过Vensim软件建立起涵盖供应商、配送中心和超市门店的三级库存管理模型。
1.1 建模目的
本文研究从供应商到配送中心直至超市最后抵达客户手中的连锁超市供应链系统库存。探究如何实现供应链各节点的信息反馈机制和有效的信息传递,寻找降低库存水平的动态因素,实现库存从供应商到配送中心再到超市的实时监控。
1.2 模型边界
本文针对超市供应链系统,考虑供应商-配送中心-超市-顾客的流程,从下游客户发出需求到超市购买,超市向配送中心发出订货需求,配送中心向上游产品供应商提出订货。供应商、配送中心和超市还有其他服务,如采购、包装、配送等环节,属于系统边界之外内容这里不做考虑。
1.3 模型的假设
①本模型针对特定商品且需求较稳定,即在一定范围内发生有限度的随机波动,不受季节等因素的影响;
②商品都是合格的,不考虑退货问题;
③商品可以按延迟时间准时到达,完成配送流程;
④不考虑连锁超市库存系统的采购、销售、运输和存储能力限制。
1.4 超市库存管理系统系统因果关系图的构建
结合前述对系统边界的确定,可以得到连锁超市库存系统因果关系图,如图1所示。
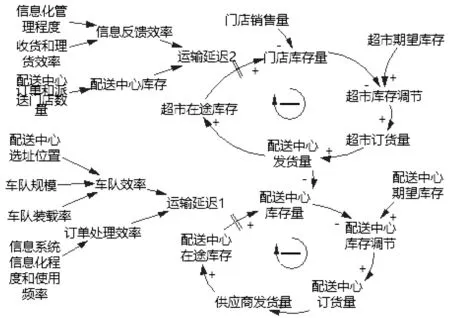
图1 库存管理系统系统因果关系图
1.5 连锁超市库存管理系统流程图构建
在分析因果关系图的基础上,构建出连锁超市库存系统仿真模型,如图2所示。

图2 连锁超市库存管理系统流程图
根据流程图中各变量之间的关系,确定供应链多级库存仿真模型方程关系如表1所示。

表1 模型方程式表
2 模型模拟与结果分析
本文以某种油作为研究对象,对模型初始值、系统仿真初始值及常量进行赋值,赋值结果如表2所示。
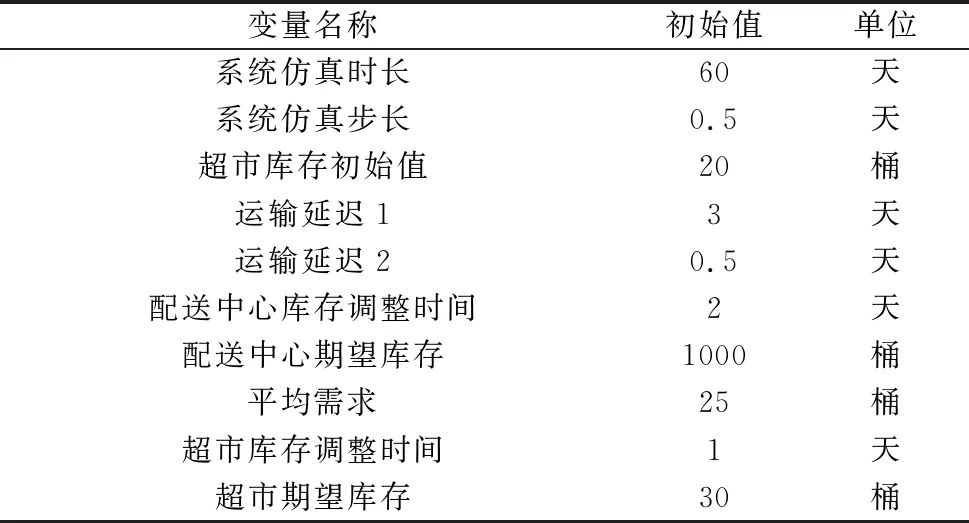
表2 模型初值总表
运行Vensim软件并得到以下结果:
从图3中可以看出,超市库存存在严重不真实状况,供应链整体信息反馈速率降低,信息的不真实性开始出现并放大。针对供应链多级库存管理中经典的牛鞭效应问题,本文运用上述模型,通过调整相关变量,例如调整运输延迟1(记为TL1)、运输延迟2(记为TL2)和配送中心库存调整时间(IAT),观察这些变量对库存和牛鞭效应的影响。

图3 初始超市库存曲线
2.1 调整TL2
基于调整单一变量的准则,其余变量设定保持初始状态,仅对TL2进行调整,分别将其设置为0.25天和0.6天,运行结果如图4、图5所示。
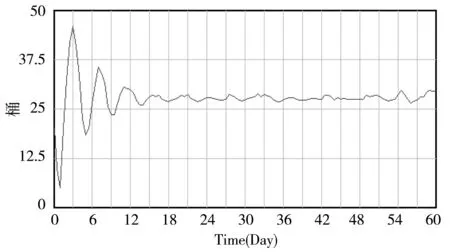
图4 TL2=0.25天超市库存曲线图
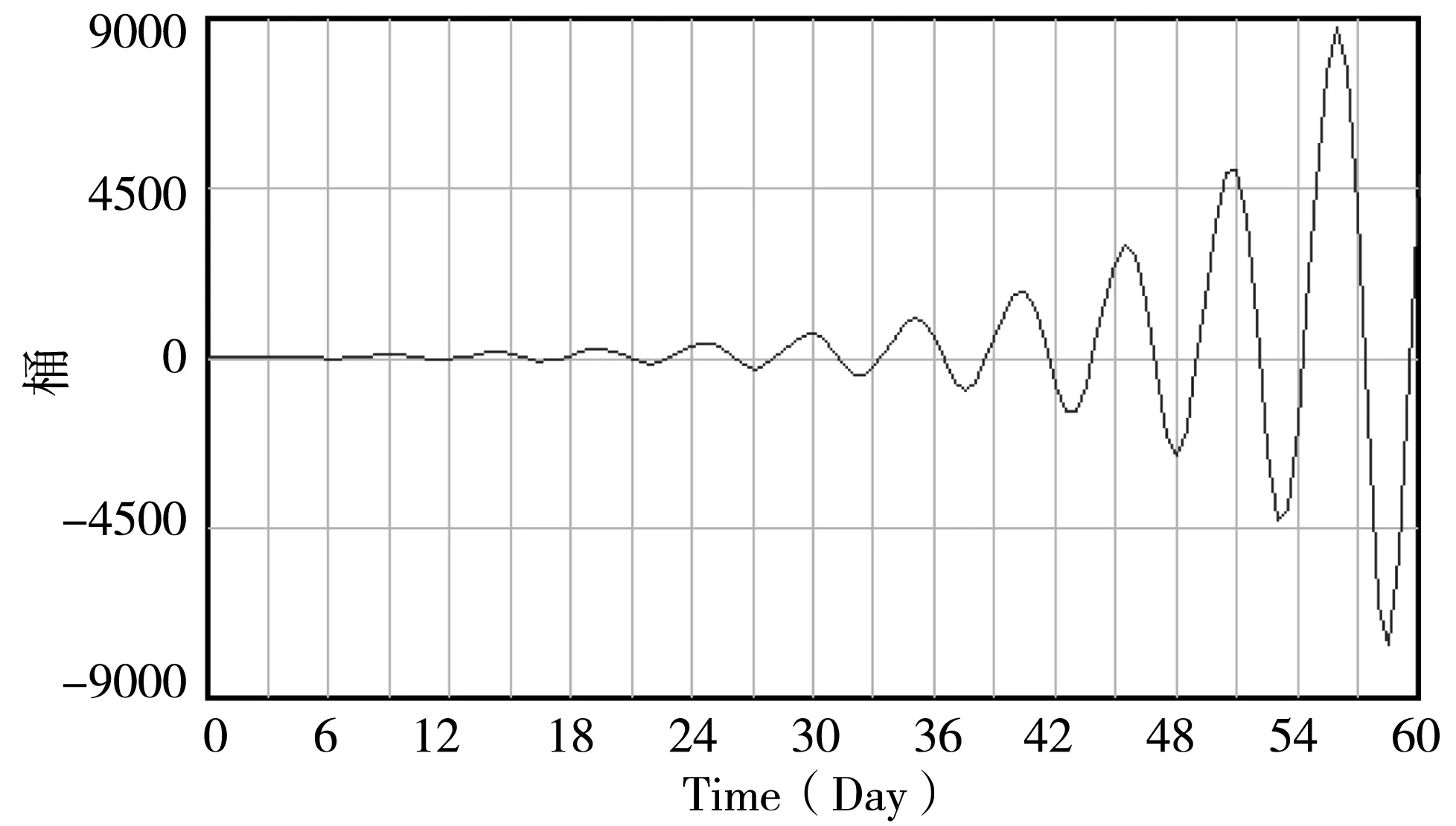
图5 TL2=0.6天超市库存曲线图
从图4可以看到,TL2=6h,超市库存始终保持正值,即不会缺货状态,是理想库存状态。系统经过前期不稳定波动,随后保持在库存量大于25件的小范围内波动,而平均需求是25件/天,此时正好可以保持良好的供应状态。延长TL2至0.6天,库存波动非常大,系统处于极度不稳定状态,从库存量和缺货量来看,与超市库存实际严重不符,导致牛鞭效应增强。
2.2 调整TL1
保持TL2设置为0.25天,TL1初始值为3天,其余初始值不变。分别将TL1设置为2天和1天分别进行模拟,由于TL1为配送中心在途库存延迟时间,故配送中心存货模拟结果输出如图6所示。

图6 配送中心存货对比图
曲线1-3分别对应TL1等于1天、2天、3天的情况。经仿真模型运行可知:随着TL1的增大,库存波动在变小,库存水平进一步降低,系统运行更加平稳。对于配送中心本身而言,配送中心货物众多,适当延长配送中心货物在途时间能够维持库存的稳定变化,降低库存管理复杂度,便于仓储人员管理,有助于实现经济效益最大化。
2.3 调整配送中心库存调整时间
IAT初始值为2天,分别调整为1天和5天的情况,运行模型并保存输出结果,依次对应图7中的曲线3、曲线2和曲线1。
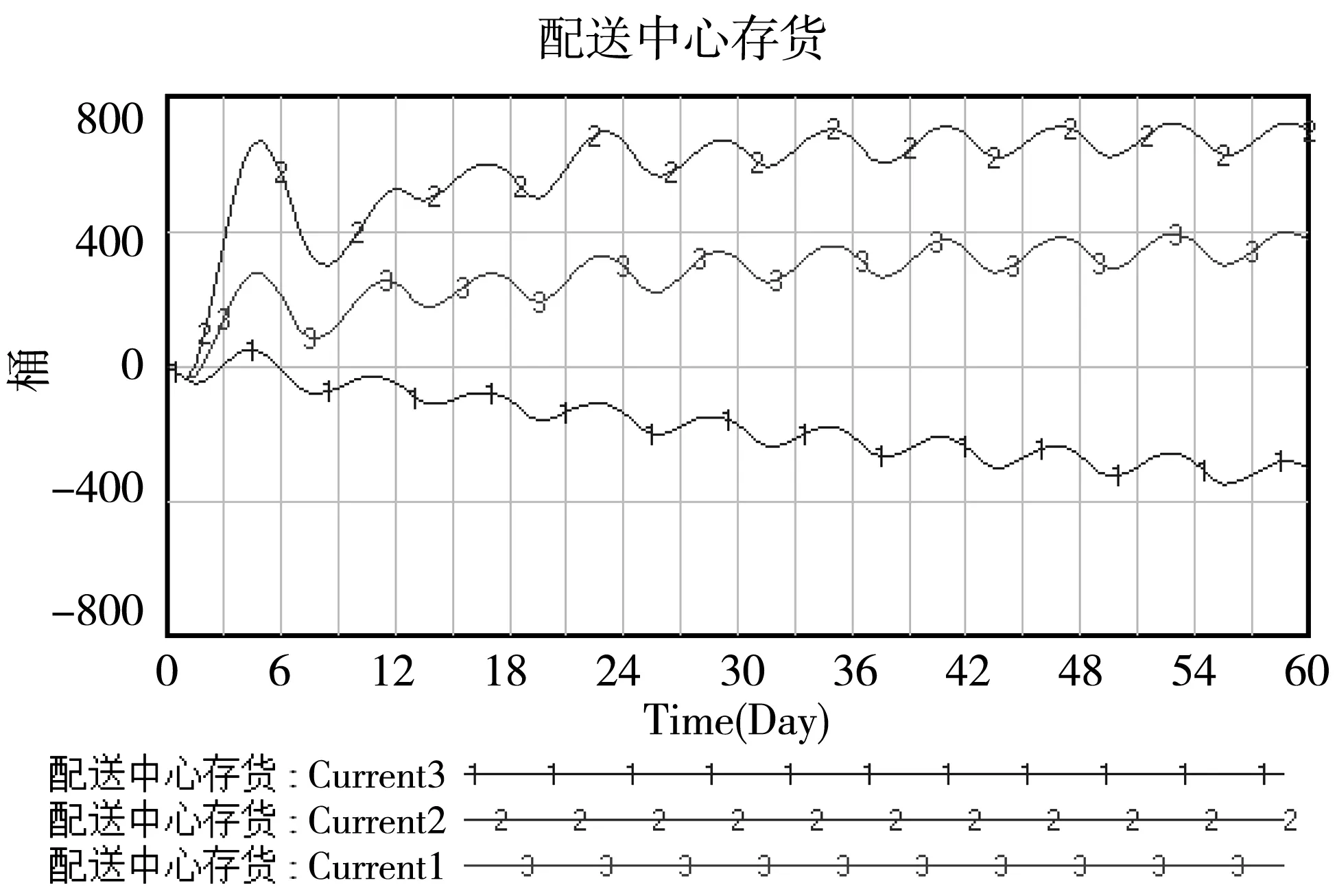
图7 配送中心存货对比图
当IAT增加到5天时,配送中心已经完全处于缺货状态,这意味着过长的库存调整时间不能满足库存供应,不符合实际情况。当IAT=1天时,货物流动速率加快,库存量保持较高水平。这对配送中心仓库的仓储能力和人员管理造成压力,要求在一天之内对库存进行调整,需要更多的配送车辆和人员。同时观察到IAT=2天时,库存水平下降明显且平均库存较小。
从总的延迟天数来看,适当延长IAT能够提高系统整体的稳定性,进一步延长IAT却是以降低供应链整体反应能力为代价的,而往往使得系统反馈不足造成缺货现象。由此可见,在合理的范围内,适当缩短配送中心库存调整时间,能够减轻库存压力,同时提高系统的时效性,有利于缓解需求放大效应。
3 模型优化总结
从上述3个方案的仿真结果来看,一味降低货物在途延迟时间并不一定是缓解库存压力的好方法,有些阶段的延迟时长变化会明显缓解牛鞭效应,有的则会带来更大的库存积压。所以就货物在途时长而言,需要根据实际情况进行恰当的处理。对于库存周转时长而言,企业可以根据不同产品的性质来合理安排出入库时间。总体来说,该模型降低了供应链三级库存系统的库存量,并很好地缓解了缺货情况,增加了供应链节点间的信息传递。
连锁超市库存系统改进措施如下。
一是采取库存集中控制管理[7],建立仓储配送范围和终端配送能力能够覆盖全销售门店的全品类集中仓库,以集中库存布局高效率应对市场需求的变动,提高配送效率,同时缓解企业供需不匹配的问题。
二是建立信息化库存管理系统。将区块链技术[8]应用于库存数据处理,区块链相当于提供了一个共享数据库,将供应链多个节点链在一起,构成数据资源共享的多层次、多功能和多元化链式组织,该组织能够强化相关主体沟通、增加物流透明度和数据资源可信度。
三是采取联合库存管理策略。供应链上多点库存转化为核心企业库存,共同制订库存计划,供应链分为上游和下游两个库存协调管理中心,借助信息化库存管理系统平台的共享信息实现集成化的库存管理,缓解需求放大现象。
4 结语
通过构建连锁超市供应链三级库存管理系统动力学模型,得出了不同延迟时间和库存调整时间对连锁超市系统整体库存的变化规律,能够较好地模拟实际系统状况。通过分析不同情况下库存量的变化情况,总结出模型优化结果,可以对实际连锁超市系统提供一定的实施措施建议。
本文的不足之处:由于连锁超市库存管理系统涉及的因素众多,关系复杂,其他复杂因素并未考虑其中,比如供应链中更多层级库存和运输距离问题。在以后的研究工作中将在这方面继续进行深入探索。
