基于系统动力学的城市地下智能物流系统仿真研究*
2022-03-15颜浩龙
□ 颜浩龙,王 晋
(湖南工业职业技术学院,湖南 长沙 410208)
随着社会的进一步发展和城市规划的不断优化,将城市地下智能物流系统纳入到新型城市规划中是完善城市功能的必然发展趋势,因此学术界与企业界关注城市地下智能物流系统理论与应用的学者专家越来越多。城市地下智能物流系统的配送网络的多级HUB结构模式是城市地下智能物流系统的规划与设计的重要组成部分,HUB组合模式的设计关系到总站和地下各级HUB的建设规模,并且直接决定了各级HUB的最大负荷和配送轨道结构形式。
1 文献综述
国内外学者对城市地下物流的研究已经取得了一定成果,国内学者李彤、王众托[1]以斯坦纳最小树(SMT)为理论模型,建立了符合我国大型城市不断扩展这一特点的树状地下物流网络布局模型,并通过对国际公布的STEINLIB实例数据计算并与蚁群算法和模拟退火算法进行比较研究。曾令慧、周爱莲[2]研究了地下物流网络运输过程中的运输工作量、时间费用、运输能力和最长时间的约束条件下的以运输费用和运输时间最小化的目标函数优化模型。易美、周爱莲[3]以物流设施建设成本、运输费用及中转服务费用最低为目标函数,以物流设施的节点、运输管道容量限制及管道路线最长限制等为约束条件构建一个数学模型。曾令慧、周爱莲[4]研究了地下物流网络运输过程中的运输工作量、时间费用及中转延误,合理设置最大运输能力和最长时间的约束条件,建立运输费用和运输时间最小化的目标函数优化模型。李昊、张恒旭[5]研究了地下物流网络在该地的构建方法,建立了地下物流节点选择模型,完成了地下物流通道设计,优化了地下物流网络系统,讨论了建设时序与动态优化的方法。华云、董建军[6]以ULS网络的经济、效率、便利、协同为目标,基于解释结构模型分析影响因素间的关系,构建了多级递阶结构模型。包敏[7]采用图论、最优化方法等理论建立了基于集合覆盖度的地下物流各节点选址模型,并设计了基于Floyd算法和主目标法的求解算法。童胜昌[8]针对城市地下物流网络优化问题,构建了以网络可用性、网络可达性、网络适应性为一级指标的三维网络效率评估模型指标体系。刘川昆等[9]结合国内外地下物流系统研究成果,基于路径优化与运输成本建立了以总成本最小为优化目标的线性规划模型。方龙祥、于雪雨[10]研究以合肥市二环及周边区域的数据为例构建了集合覆盖模型,并采用0-1整数规划算法确定地下物流系统网络节点的分布。娄晓梦、周爱莲[11]以政策审批、工程地质、经济、环境、技术与施工这5项可能引起重大风险的因素对地下物流系统建设建立评价指标体系,并通过熵权法、模糊数学方法对系统建设风险进行综合评价。颜浩龙、王晋[12]运用集覆盖理论构建了配送到户的城市地下物流交通网络,采用三级HUB的结构解决城市内地面收货终端分布不均衡的问题。任睿等[13]针对一类轴辐式地铁-货运系统(M-ULS)网络提出三阶段布局优化方法,并建立熵权-TOPSIS模型筛选地下货运流量,构建网络选址-分配-路径组合优化模型。
综上所述,国内外专家学者关注城市地下物流研究已有一定的时间,积累了一定的实践经验和理论成果,但是受工程技术的限制,早期的城市地下物流系统规模较小,功能也比较单一。随着近年来工程装备与技术的飞速发展,当代社会已具备大规模建设城市地下物流系统的技术能力与经济实力,对城市地下物流系统的完整理论研究开始变成一个比较迫切的问题。当前已有的相关研究成果主要集中在地下节点选址、网络优化和项目可行性等方面,以城市地下物流系统项目实施为目标的相关研究还较少,特别是对城市地下物流系统的各级HUB的协同规划与最大负荷等方面的研究还相当匮乏。
2 城市地下物流系统系统动力学建模
2.1 物流量的估算
城市地下物流对象范围设定为超市、快递、餐饮。城市规模以某市主城区人口密度为例,20000人/平方公里,1500亩/小区,每个FDC(三级HUB)联接10个小区,即10平方公里,每个RDC(二级HUB)联接10个FDC(三级HUB),共500平方公里,总人口1000万。
①快递量估算。人均每日消耗的快递物流量:快递人均1件/天,平均每个快递包装箱按20cm*20cm*40cm计算,即0.016立方米,每个小区日均快递量估算为320立方米/天。每个FDC日均物流量3200立方米,每个RDC日均3.2万立方米,整个城市日均16万立方米。
②超市物流量估算。人均物流量按0.01立方米/天估算,每个小区日均超市快消品消耗量估算为200立方米,每个FDC日均超市快消品物流量2000立方米,每个RDC日均2万立方米,整个城市日均10万立方米。
③餐饮物流量估算。人均物流量2KG/天,折合为0.002立方米/天,每个小区餐饮物流量估算为40立方米,每个FDC日均餐饮物流量为400立方米,每个RDC日均4千立方米,整个城市日均2万立方米。
综上所述,平均每个小区DC每天的三类货物物流量估算汇总为560立方米,每个FDC的日均物流量为5600立方米,每个RDC的日均物流量为5.6万立方米,整个城市的日均物流量估算为28万立方米。
2.2 集装设备装载分析
城市地下物流系统的集装设备选型对象主要考虑20尺普柜和托盘,20GP集装箱内部容积为33立方米,按装载28方估算,托盘采用1米*1.2米的标准托盘,每托盘堆码量按2立方米估算。整个城市每天物流总量28万立方米,即1.4万GP/天,每个集装箱长度按7米计算,货列总长度为98千米。配送批次设计如下:
①按4小时每批次配送。每天平均配送3次,每4小时集中配送1次,每次配送0.47万集装箱,每个集装箱长度按7米计算,按每天早、中、晚三个批次计算,每个批次要送货33.67千米。按一级轨道额定速度80千米/时计算,每批需要0.42小时完成发车,按5个RDC计算,平均每个RDC每次接受货物933集装箱,每个RDC覆盖10个FDC,平均每个FDC每批接收货物93.3集装箱,每个FDC覆盖10个小区,平均每个小区每批接收货物9.33集装箱。
②按每小时一个批次配送。每天平均配送12次,每次配送1167集装箱,每批货列长度为8.16千米。按一级轨道额定速度80千米/时计算,每批需要0.1小时完成发车,按5个RDC计算,平均每个RDC每次接受货物233集装箱,每个RDC覆盖10个FDC,平均每个FDC每批接收货物23.3集装箱,每个FDC覆盖10个小区,平均每个小区每批接收货物2.33集装箱。
2.3 基本假设
①以1小时为周期进行定时分批的发送;
②以托盘为基础装载单元设备;
③地下物流系统每天按12小时工作时间计算;
④城外货物输入按一定范围内的随机函数设定。
2.4 系统动力学建模
采用美国VENTINA公司的VENSIM6.3版对城市地下智能物流系统配送网络进行仿真建模如图1所示。

图1 城市地下智能物流系统动力学流图
3 城市地下物流系统系统动力学模型仿真
3.1 仿真目标
城市地下智能物流系统系统动力学仿真主要是为了四个方面的目标:①模拟不同模式下整个系统的通过能力问题,获取各模式下保持通畅的关键数据,并以此为基础研究各HUB每批货物的处理能力;②模拟不同输入情况下各HUB设施的货物缓存量,并以此为依据在下一步研究中研究各级HUB的设计问题;③对三种模式进行对比分析,并根据对分析,研究不同情况下的三种模式的优势与不足;④研究整个地下物流系统配送能力的主要限制因素是哪些。仿真过程中的基本参数设定如表1所示。

表1 系统动力学仿真基本参数设定
3.2 仿真过程
分别仿真以下几种情况:①CDC额定输入,RDC、FDC、小区DC等各级HUB均呈均匀分拨时的峰值测试;②CDC随机输入,RDC、FDC、小区DC等各级HUB均做呈均匀分拨时的峰值测试;③CDC随机输入,RDC、FDC、小区DC均做极限变化时的峰值测试。
3.3 仿真结果
3.3.1 四级分拨模式的仿真结果分析
“CDC——RDC——FDC——小区DC”的四级分拨模式的仿真结果如图2所示,曲线1,CDC额定输入,RDC、FDC均呈均匀分拨时的峰值测试;曲线2,CDC输入随机增大,RDC与FDC均做呈均匀分拨时的峰值测试;曲线3,CDC输入随机增大,RDC与FDC均做极限变化时的峰值测试。测试结果表明:①主要瓶颈是各级HUB的处理能力,即对货物的分拣、装卸和发车的能力,在这种模式下,每个HUB都有爆仓的可能,例如,小区DC爆仓时会影响到上级FDC的发货,而FDC的爆仓又会引起上级RDC的爆仓,RDC的爆仓则会引起总基地的爆仓;②各小区DC、FDC、RDC的物流量的不均衡会引起局部爆仓,如,在外部基地额定的处理能力内,由于各RDC物流量的不均衡,可能会在某RDC发生爆仓现象,同理,在某RDC处理能力内,由于下级各FDC的需求量不均衡,可能在某FDC形成爆仓,在某FDC处理能力内,由于下级各小区DC的需求量不均衡,也会在某小区DC形成爆仓;③由于地下各级HUB的内部空间建设的建设成本较大,因些在建设地下物流系统时,需要设计好足够的拓展空间,随着物流量的增加,用于扩大各级HUB的缓冲量和处理能力,主要是各节点区域和轨道预留足够的拓展空间;④CDC输入随机增大,且RDC、FDC分拨同时随机时,会形成三重峰值叠加的效应,造成各级HUB货物输入量极速增大,当CDC突然增加2.2倍时,随机时,RDC增幅峰值达7倍,FDC增幅峰值达11倍,均衡情况下RDC增幅为1.8倍,FDC增幅为1.8倍。

图2 四级分拨下的仿真结果图
3.3.2 三级分拨模式的仿真结果分析
“CDC——FDC——小区DC”的三级分拨的仿真结果如图3所示,曲线1,CDC额定输入,FDC均呈均匀分拨时的峰值测试;曲线2,CDC输入扩大,FDC做呈均匀分拨时的峰值测试;曲线3,CDC输入扩大,FDC做极限变化时的峰值测试。测试结果表明:①在CDC额定输入而FDC随机的情况下,当总输入量超过FDC最大处理能力时会形成爆仓,此时FDC的处理能力成为瓶颈,建设时需要留足拓展空间;②当CDC额定输入,各FDC输入均衡,但是各小区DC随机时,物流量超过小区DC设计最大额度时会爆仓,此时小区DC的处理能力成为瓶颈,建设时需要预留拓展空间;③CDC输入随机增大,且FDC分拨同时随机时,会形成二重峰值叠加的效应,造成各级HUB货物输入量极速增大,当CDC突然增加2.7倍时,随机时,FDC增幅峰值达6.1倍,均衡情况下FDC增幅为2.2倍。
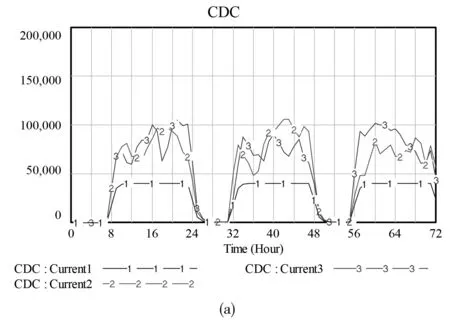
图3 三级分拨下的仿真结果图
3.3.3 二级分拨模式的仿真结果分析
“CDC——小区DC”的二级分拨的仿真结果如图4所示,曲线1,CDC额定输入,FDC均呈均匀分拨时的峰值测试;曲线2,CDC输入扩大,FDC做呈均匀分拨时的峰值测试;曲线3,CDC输入扩大,FDC做极限变化时的峰值测试。测试结果表明:①当CDC总输入随机波动输入,其他各级HUB稳定输入时,如果物流量超过了最大设计额度,总部基地CDC会爆仓,需要整个地下物流系统以满负荷状态运行足够的时间才能处理完,或者将部分货物以地上配送的方式完成。②在CDC输入总量不变、各小区DC随机的模式下,当小区DC输入量超过最大设计处理能力时会形成爆仓,但是小区DC通常会有较大的缓冲仓,同时还可以采用地面配送来解决爆仓情况。③CDC输入随机增大,且小区DC分拨同时随机时,会形成二重峰值叠加的效应,造成各级HUB货物输入量极速增大,当CDC突然增加2.4倍时,随机时,小区DC增幅峰值达3.4倍,均衡情况下小区DC增幅为2.3倍。
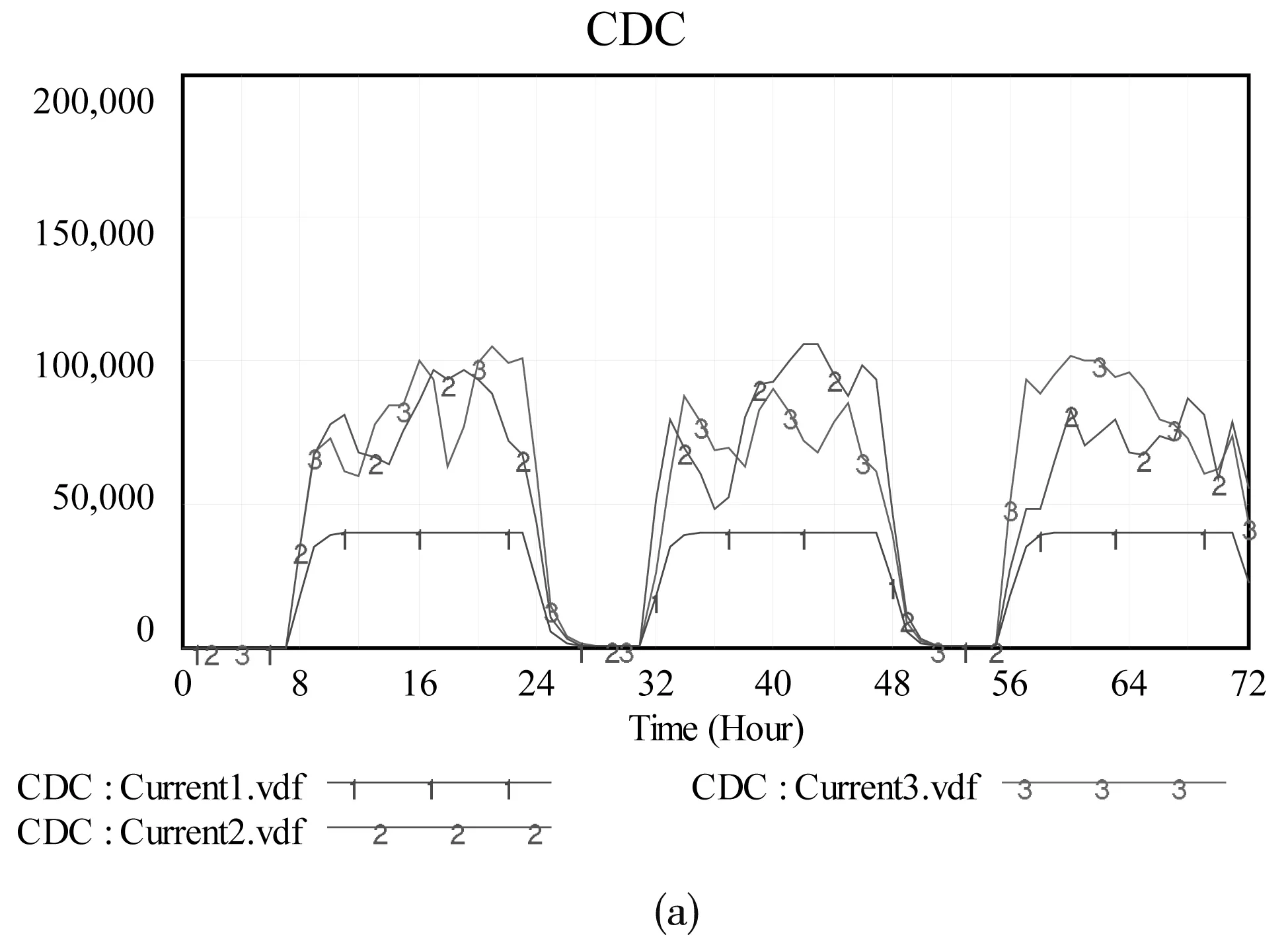
图4 二级分拨下的仿真结果图
4 结论
①城市地下物流系统配送批次问题:常规模式下的一天二批或三批的配送频率,对各级HUB的各功能区面积和容积要求较大,且不能满足同城内各种即时配送的需求,特别是对餐饮生鲜等即时补货的响应,且整个系统的配送频次调控的空间较小,基本上只能固定在一天两次或三次。而采用按小时配送模式,则对CDC和各级HUB的分拣功能要求较高,要求每小时的输出量大于输入量,如果CDC和各级HUB的即时分拣处理能力低于货物输入时,则会造成大面积配送延误情况的发生,这方面,CDC和各级HUB的分拣处理能力可以相互调节,若CDC能够全部处理完成,则以下各级HUB的分拣需求会相应减少,同理,如果CDC分拣能力达到峰值时,可以通过启用各级HUB分拣能力的方式来提高整个系统的即时分拣能力。因此,城市地下智能物流系统在设计时,整个系统每小时能处理的物流量峰值应该是所有HUB处理能力,正常工作时,可以根据物流量来动态调整启用整个系统的各级HUB站点,即三种不同模式的动态调整。
②二律背反的问题。相同时间内配送批次的增加会增加对城市地下物流网络的开行方案的要求,使之变得更加的复杂,四级HUB模式、三级HUB模式和二级HUB模式依次增加了城市地下物流系统开行方案的发车次数,而高发车频次和每列车次车厢数的减少会降低整个运输网络的总运输能力,因此需要一个动态调节模型来解决这个问题,使开行方案能随着运输量的变化而不断调整以满足配送需求。
③三种不同结构模式仿真结果对比分析显示,货物处理能力最大的模式为第三种“CDC——小区DC”二级分拨模式,这种模式将物流配送量超过最大设计值时的爆仓预设在总站和小区DC中,避免了RDC、FDC不便于处理爆仓情况的局限,同时也充分利用了总站和小区DC处理爆仓能力相对更容易的特点。
