基于贝塞尔曲线的双钢轮振动压路机轨迹规划研究*

赵方熠，高 博，赵睿英，王 欣

(1.长安大学道路施工技术与装备教育部重点实验室，陕西 西安 710064；2.西安恒翔控制技术有限公司，陕西 西安 710064)

0 引言

相对于汽车而言，工程机械的作业单一，施工场所人流稀疏，大多没有交通法规的限制，而且尘土、振动、噪声及高温等恶劣环境会影响人的健康和工作质量[1]。这使得无人驾驶与自动作业迅速成为目前工程机械领域的研究热点。轨迹规划是压路机无人驾驶的关键技术，Lemaire C等[2]提出了一种压路机路径规划的几何模型，考虑了压路机的运动学姿态和动力学约束，避免了执行器达到饱和状态；吕镇基等[3]提出了一种相切圆弧轨迹规划方法，实现了泊车所需的最小车位，并用缓和曲线解决了曲率不连续情况。

本文分析双钢轮振动压路机的碾压流程和作业要求，对比双圆弧相切轨迹、等速偏移曲线与正弦曲线叠加轨迹和贝塞尔曲线轨迹的优缺点和适用性，提出一种以曲线的曲率和曲率的变化率为约束，以曲率的最大值和最小值的差值为优化目标，以贝塞尔曲线为换道轨迹的优化换道曲线。

1 双钢轮振动压路机碾压工作流程

在道路施工中，双钢轮振动压路机通常跟随沥青混凝土摊铺机进行碾压作业，进行沥青混凝土的复压工作。碾压过程以区域压实为主，循环往复作业，碾压工艺相对固定。双钢轮振动压路机的路面碾压作业流程可表示如图1所示。假设单台压路机负责作业的路面宽度为摊铺机熨平板的宽度，碾压遍数为1遍，其中A0～H0分别代表各碾压道的起始点；A1～H1分别代表各碾压道的终点；阴影部分代表碾压相邻两道重叠的区域。

待摊铺机摊铺到合适距离后，压路机依次从区域I.1～I.4，然后从区域II.1～II.4进行碾压作业。

2 双钢轮振动压路机碾压作业要求

进行沥青路面压实时，应严格遵守压路机的操作规程和碾压作业工艺，保证作业质量达到施工要求。具体要求如下：

1)碾压过程中，应该使压路机的驱动轮朝向摊铺机熨平板一侧，即驱动轮靠近新摊铺的混合料，以减少波纹和断裂现象；

2)压路机启动加速段的加速度平稳，匀速碾压段速度恒定，停车减速段的减加速度平稳和换道时转向平稳，保证压实度均匀和压实质量良好；

3)相邻碾压道之间每次重叠的宽度为dm。

3 双钢轮振动压路机作业轨迹规划模型

3.1 碾压路线模型

根据以上作业要求，以碾压第一区域为目标，建立如图2所示的碾压路线模型。压路机在A点启动，经过第①前进加速段到达B点，使速度达到碾压要求的速度v，然后压路机匀速运行到C点，到达C点时减速，经过第③前进减速段到达D点。接下来，压路机从D点倒车加速行驶到达C点，使速度达到v，然后压路机倒着匀速行驶到达B点，从B点处开始减速至出发点A时的速度v=0。第一条道路碾压完成后，换道至相邻车道，以A点作为换道的起始点，经过第⑦换道加速段到达E点，不仅满足换道要求且速度达到v，然后，压路机按照相同模式将第二条道路完成碾压。同理，将该区域其余道路依次碾压。

由此可知，碾压过程以直线碾压为主，只有换道时需要走曲线。因此，接下来将以压路机换道为目标，对其换道曲线进行设计。

3.2 换道模型

假设双钢轮振动压路机的轮宽为D，叠轮宽度为d，则换道宽度L=D-d，换道长度为S。以换道起点为坐标原点建立图3所示的换道模型。

4 双钢轮振动压路机换道轨迹规划

由3.2节可知，压路机的换道轨迹规划问题可以转化为S型曲线设计的问题，其中压路机换道的初始状态和终端状态为

(1)

一般使用的S型曲线中，双圆弧相切曲线换道轨迹的起点和终点处曲率不为0，且两圆弧相切处曲率不连续；等速偏移曲线叠加正弦曲线轨迹虽然满足换道轨迹曲率连续，而起点和终点处曲率为0，但不能确保中间段曲线的曲率满足压路机转向所需的曲率范围。下面利用贝塞尔曲线，设计出适合双钢轮振动压路机的换道轨迹方案。

4.1 贝塞尔曲线的定义

贝塞尔曲线是由PauldeCasteljau在1959年运用deCasteljau算法开发的，由法国工程师PierreBezier在1962年发表，主要用于汽车的主体设计[4]，现在也广泛应用于动画制作和智能机器人轨迹规划等领域。

贝塞尔曲线是一组由控制点作为顶点的多边形且被多边形包围的曲线。在一空间内，有n+1个由Pi(i=0，1，2，…，n)表示的控制点，则这n+1个控制点所形成的贝塞尔曲线方程可表示为：

(2)

其中，u为位置参数；Bi，n(u)为n次Bernstein基函数。对公式(2)求一阶和二阶导数得：

(3)

(4)

将u=0，1带入公式(3)、公式(4)，求出两端点处的导数：

(5)

(6)

(7)

(8)

由参数式给出的任意点曲率公式为：

(9)

其中，τ∈[0，1]为位置参数。将式(5)-式(8)带入式(9)，求得起点和终点的曲率为：

(10)

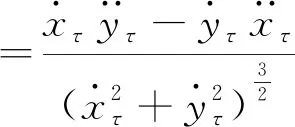
(11)

4.2 贝塞尔曲线控制点的计算

根据压路机的换道模型，设q=[q(1)，q(2)，q(3)，q(4)]。其中，q(1)为x的坐标，q(2)为y的坐标，q(3)为压路机的航向角；q(4)压路机作业轨迹的曲率。

设初始状态为q0=[0，0，0，0]，终点状态为q0=[S，D-d，0，0]，本文采用七阶贝塞尔曲线进行换道模型点对点的轨迹规划任务，因此需要先确定8个控制点的坐标。

根据起点q0=[0，0，0，0]，可得第一个控制点：

(12)

为满足起点的航向角约束φ0=0、速度约束v0=0、曲率约束ρ(0)=0，根据公式(5)、公式(10)，可得第二和第三个控制点：

(13)

(14)

同理，对于终点q0=[S，D-d，0，0]，可得第六、七、八个控制点坐标：

(15)

(16)

(17)

其中，vg为终点速度。

以上完成了满足起点和终点约束的控制点设置，但中间曲线状态还未能控制，选择4个自由变量来描述控制中间曲线状态的第四和第五个控制点，则：

(18)

(19)

综上所述，通过确定P0、P1、P2、P5、P6、P7满足压路机起点位姿和终点位姿，然后通过控制4个自由变量确定中间曲线的走势，可以得到一条唯一确定的贝塞尔曲线。

4.3 贝塞尔曲线的优化

压路机的实际转向过程受自身结构(最小转向半径)、系统响应(转向速度)和作业要求(曲率连续)等条件影响。以这些条件为约束，通过优化的方法，求解出满足压路机行走性能的曲线。

围手术期有效镇痛是实现ERAS的核心内容。术后疼痛的发生不仅严重影响患者机体各系统的功能，而且也严重制约了患者的快速康复。因此，快速康复相关专家共识中有多项条款均与镇痛有关。有研究显示，国外约77%以上的患者经历术后镇痛，其中80%的患者为中-重度疼痛。国内90%以上患者经历术后中-重度疼痛。因此，围手术期，尤其是术后有效镇痛是促进患者快速康复的关键因素之一。

1)约束条件的建立

换道轨迹应满足压路机的最小转向半径，且转向速度不能大于最大转向速度。所以，规划轨迹的曲率应小于最小转向半径所对应的曲率，曲率的变化率小于最大转向速度下的曲率变化率。因此，对曲率及其变化率建立约束条件：

(20)

d1、d2、d3和d4需满足：

(21)

2)优化目标的建立

根据以上参数化的方法，最终建立了使用d1、d2、d3、d4确定满足位置约束和姿态约束的轨迹。本文使用最优化的方法求解出满足约束的4个参数，采用的优化目标为[5]：

J(q0，qf，d1，d2，d3，d4)=ρmax(τ1)-ρmax(τ2) ，

(22)

其中，τ1和τ2是分别使曲线曲率最大和最小的参数。曲率对应着压路机的航向角，因此优化目标的含义是使曲线曲率即压路机航向角的变化量最小。

3)曲线仿真

根据以上分析，该问题属于有约束条件下的最小化问题。采用MATLAB优化工具箱中的fmincon优化函数对该问题进行优化，则该问题可以描述为：

Minimize：J(q0，qf，d1，d2，d3，d4)

(23)

以YZC3双钢轮振动压路机为研究对象，选取S=5 m，D=1.2 m，d=0.6 m和Rmin=4.8 m，则q0=[0，0，0，0]，qf=[5，0.6，0，0]。仿真得到基于贝塞尔曲线的换道轨迹如图4所示，航向角变化如图5所示，曲线的曲率变化如图6所示。

由图4、图5、图6可知，规划轨迹连续；航向角变化连续，且初始和终了时刻航向角为0；轨迹曲率连续，曲率最大没有超过0.2，且在初始和终点位置曲率为0。综合以上，设计所得轨迹满足设计要求。

5 结论

本文分析了双钢轮振动压路机的碾压流程，结合碾压作业要求，建立了双钢轮振动压路机的作业轨迹模型，包含直线和换道曲线两部分。为克服双圆弧相切轨迹、等速偏移曲线与正弦曲线叠加轨迹的缺点，将贝塞尔曲线作为换道轨迹曲线，把曲线的曲率及其变化率作为约束，以曲率的最大值和最小值的差值作为优化目标，对曲线进行了优化，得到了满足要求的压路机换道曲线。