自适应抗扰算法的四轮驱动EV转矩控制研究

龙云泽,封进,张瑞宾,韦韬

(桂林航天工业学院 汽车工程学院，广西桂林 541004)

四轮独立驱动电动汽车(Electric vehicle, EV)因其具有车辆结构紧凑、动力传递效率高、驱动策略多样化的优点,在过去的十多年中已成为全球汽车领域研究热点[1]。分布式驱动EV的驱动控制对象是四个轮毂电机(或轮边电机),具有驱动的方式直接、整车驱动模式智能可控等优点。针对四轮独立驱动EV转矩分配控制研究主要目的是实现车辆质心侧偏角、车辆侧倾角速度、横摆加速度等参数的最优化,从而实现整车动力性及经济的提升[2-4]。由于车辆行驶过程中结构及外界不确定干扰因素的长期存在,使得整车动力学理想模型与真实情况产生偏离,因此对分布驱动EV动力学模型参数扰动及环境干扰等问题的研究具有重要意义。

近年来,国内外学者对四轮独立驱动EV转矩控制的研究主要集中在稳定性控制及能耗最优控制[5-7]。滑模控制广泛运用于车辆的力矩分配控制,由于滑动模态可设计且与对象参数及扰动无关,使其具有响应快、抗扰性强、无需系统在线辨识、物理实现简单的优点,但状态轨迹难以严格沿着滑动模态面向平衡点滑动从而产生抖振现象[8]。模糊控制可实现非线性控制且不依赖精确数学模型,近年来广泛运用于汽车控制,但算法模糊规则及隶属函数的设计全凭经验,较难保证控制精度和系统动态品质。最优控制、鲁棒控制、序列二次规划法等多种控制方法被用于四轮独立驱动EV转向和直接横摆力矩控制,取得了较好的控制效果[9],但普遍存在对整车动力模型参数依赖性较强、对行驶工况变动影响不考虑的问题。

为研究四轮独立驱动EV参数扰动影响问题,建立车辆二自由度整车动力学模型,设计线性二次型最优控制器,实现汽车对理想二自由度模型横摆稳定性参数的跟踪控制。基于李雅普诺夫系统稳定理论设计自适应转矩控制器,实现车辆抗扰转矩优化分配。并运用CarSim与MATLAB/Simulink联合仿真平台进行仿真实验,验证该方法的有效性。

1 四轮独立驱动EV动力学模型

二自由度整车动力学模型反映车辆转向行驶时的操纵稳定性理想动力学响应,结合整车结构参数,将其作为自适应控制系统的参考模型。在二自由度模型基础上考虑横摆角速度与质心侧偏角两个主要参数的理想取值,获得理想二自由度期望模型。

1.1 二自由度整车动力学模型

所设计控制系统目标是研究整车行驶过程参数非线性对操纵稳定性的影响及系统自适应控制能力。模型考虑整车侧向运动、横摆运动自由度。搭建分布式驱动EV二自由度整车动力学模型,如图1所示。

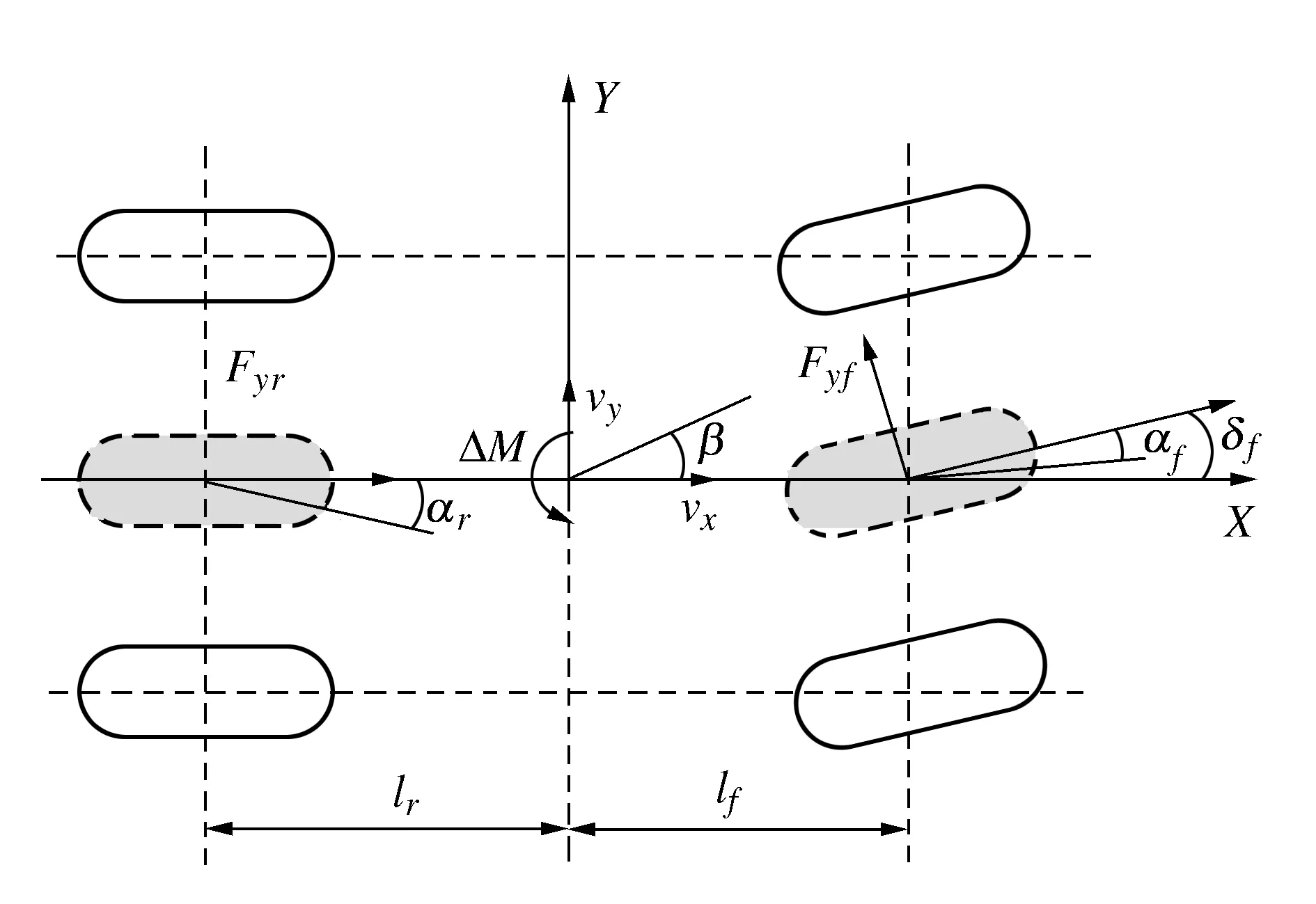
图1 四轮独立驱动电动汽车二自由度模型

模型作了以下近似:1)忽略整车垂向运动、绕y轴的俯仰运动、绕x轴侧倾三个运动的影响;2) 忽略滚动阻力、风阻影响; 3) 假设两前轮具有相同的转向角和侧偏角、两后轮的侧偏角一致;4) 采用传统的前轮转向方式; 5) 假设各轮胎动力学特性一致,且轮胎侧偏特性处于线性范围内。二自由度整车动力学方程表达如下[10-11]:

(1)

(2)

may=Fyf+Fyr

(3)

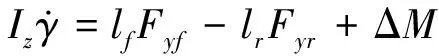
(4)

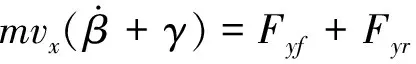
(5)

Fyf=Cfαf,Fyr=Crαr

(6)

(7)

(8)

(9)

式中;vx为整车纵向速度;vy为整车侧向速度;γ为整车横摆角速度;ax为纵向加速度;ay为侧向加速度;Fyf、Fyr分别为两前轮侧向合力、两后轮侧向合力;m为整车质量;ΔM为主动附加横摆力矩;β为质心侧偏角;δf为前轮转向角;αf、αr分别为前轮轮胎侧偏角、后轮轮胎侧偏角；lf、lr分别为质心至前轴距离、质心至后轴距离；Cf、Cr分别为两前轮合侧偏刚度、两后轮合侧偏刚度;Iz为整车绕z轴的转动惯量。

联立式(1)～式(9),可得二自由度整车动力学模型状态空间表达式为

(10)

式中:x=[βγ]T;u=[δfΔM]T;

1.2 二自由度整车动力学期望模型

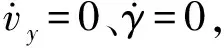
(11)

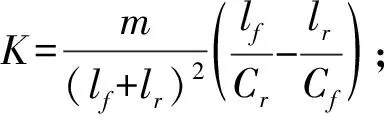
2 四轮独立驱动EV动力学模型

搭建分层式车辆控制系统,其中上层控制器中的线性二次型最优控制器计算出车辆跟踪理想横摆稳定性参数的控制量,并计算得出所需的附加横摆力矩。考虑整车在不同工况时质量与整车绕z轴的转动惯量非线性扰动情况,设计基于李雅普诺夫理论自适应控制器,通过设计前馈控制器与反馈增益控制器参数,实现自适应跟踪整车动力学理想模型状态变量。下层控制器为电机转矩分配控制器,实时分配四个车轮驱动转矩,使整车产生所需的附加横摆力矩,提升车辆操纵稳定性。分层式车辆控制系统结构原理如图2所示。

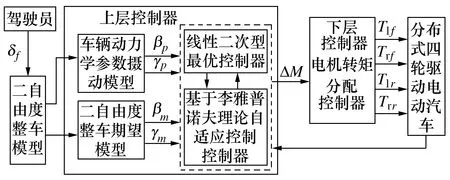
图2 分层式车辆控制系统结构原理图

2.1 线性二次型最优控制器设计

线性二次型最优控制器是一种动态优化控制器,其目标函数是系统的状态及控制量。针对汽车横向稳定性问题的控制,是一种时间终端不固定的无限时间线性二次型最优控制问题。联立式(10),建立控制目标函数为

(12)

式中:Q为半正定对称权矩阵;R为正定对称权矩阵。式(12)积分中第一项为目标跟踪误差项,第二项为跟踪能量最优控制项。线性二次型最优控制的Riccati方程为

PA+AT-P-PBR-1BP+Q=0

(13)

式中P为常正定矩阵。求解Riccati方程,可获得P矩阵的值。可得最优控制规律为

(14)

由式(14)可得汽车在行驶过程中,参数为时不变常数的最优控制量u*。将ΔM*分配给车辆独立驱动的四轮毂电机,实现对横摆稳定性的实时优化。

2.2 基于李雅普诺夫理论自适应控制器设计

在线性二次型最优控制器的基础上,设计自适应控制器,保证系统参数时变时控制器自适应调节能力。李雅普诺夫系统稳定性理论是控制系统设计的有效方法,基于该方法的自适应控制器的设计关键在于构造出合适的李雅普诺夫函数并确保该函数的导数负定或半负定。考虑质量与整车绕z轴的转动惯量两个参数摄动的整车动力学模型,自适应控制器参照自适应规律调整前馈矩阵 和反馈矩阵,实现控制对象动态特性与期望模型相一致。自适应控制器的系统结构原理如图3所示。

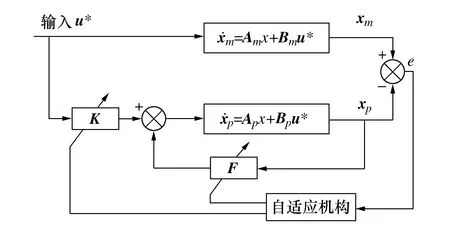
图3 自适应控制器原理图

由图3中自适应可调控制系统可得整车状态向量控制规律如下:

(15)

e=xm-xp

(16)

(17)

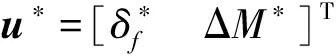
式(17)右端为零,使控制系统取得理想值,可得控制系统增益矩阵理想值及相应的系统状态误差向量:

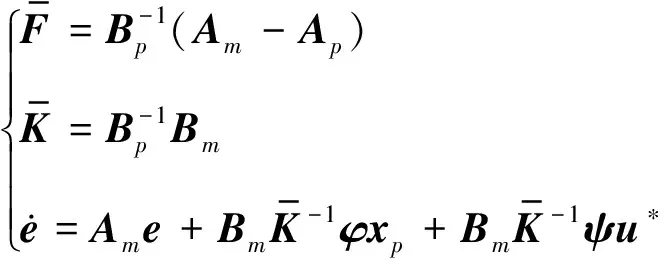
(18)

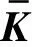
基于李雅普诺夫稳定性理论,为保证系统控制过程中系统稳定性,需寻找正定的且其导数为负定的李雅普诺夫函数。选取李雅普诺夫函数,并求得其导数的表达式为:

(19)

式中:Py、ζ1、ζ2为均正定对称矩阵;tr为矩阵求迹运算符号。

令李雅普诺夫函数导数为负定,自适应控制系统同时可满足自适应控制要求和系统稳定性要求。可得满足要求的自适应控制规律为:

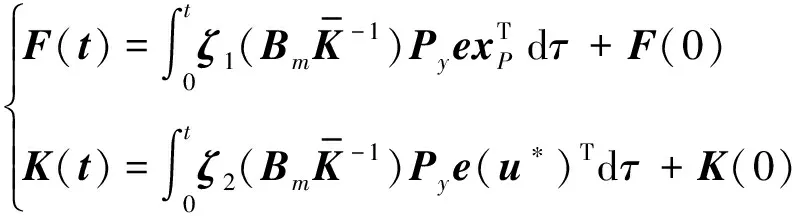
(20)

式中:K(0)为前馈增益矩阵初值;F(0)为反馈增益矩阵初值。所设计自适应控制器,能实现控制对象在参数扰动情况下自适应调节增益矩阵,使控制对象状态与期望值保持一致,并同时使控制系统满足全局渐近稳定要求。

2.3 电机转矩分配下层控制器

四轮独立驱动电动汽车具有多种驱动模式,在低附着路面及复杂路面行驶时,整车的稳定性及安全性保障较为复杂。上层自适应控制器实时计算出整车所需附加横摆力矩,通过下层四轮驱动力矩的差别分配,可实现主动整车操纵稳定性提升。搭建分布式驱动电动汽车车轮运动学模型如下:

(21)

式中;Iw为车轮转动惯量;ωlf、ωrf、ωlr、ωrr分别为左前轮、右前轮、左后轮、右后车轮转动角速度;Tlf、Trf、Tlr、Trr分别为左前轮、右前轮、左后轮、右后轮驱动转矩;Flxf、Frxf、Flxr、Frxr分别为左前轮、右前轮、左后轮、右后轮纵向力;Tlbf、Trbf、Tlbr、Trbr分别为左前轮、右前轮、左后轮、右后车轮制动转矩;Re为车轮滚动半径。

转矩分配下层控制器采用四车轮同时分配附加转矩的方式实现将主动附加横摆力矩分配到各轮上。当ΔM不为零时,根据其方向及前轮转向角,实施力矩分配[12-13]。车轮的制动转矩调节要求能准确检查其控制量,实现较为复杂。采用调节车轮驱动转矩的分配的方法精度较高且控制易实现,控制逻辑如表1所示。

表1 整车动力学模型关键参数

根据表1,主动附加横摆力矩ΔM的方向决定四车轮的转矩分配。当ΔM=0时,转矩分配控制器不工作,四轮驱动转矩平均分配。根据ΔM方向,设计控制器转矩分配关系为:

(22)

式中：ΔTlf、ΔTrf、ΔTlr、ΔTrr分别为左前轮、右前轮、左后轮、右后轮的驱动转矩调整值;D为前后轮轮距。

3 仿真试验验证

CarSim为一款专业的车辆动力学仿真软件,具有高效的建模与模拟流程,其仿真结果被国际众多汽车制造商和零部件供应商所采信。基于CarSim与MATLAB/Simulink联合仿真平台,搭建四轮独立驱动EV转矩自适应控制试验平台,选用CarSim软件中自带的一款B型车作为试验对象。在CarSim中设置整车模型的动力来源为四车轮转矩,通过将转矩输入接口链接至Simulink软件实现动力输入。Simulink软件中所搭建自适应抗扰控制算法所需整车传感器数据通过CarSim软件实时提供[14]。所搭建整车动力学模型关键参数如表2所示。搭建CarSim与Matlab/Simulink联合仿真如图4所示。

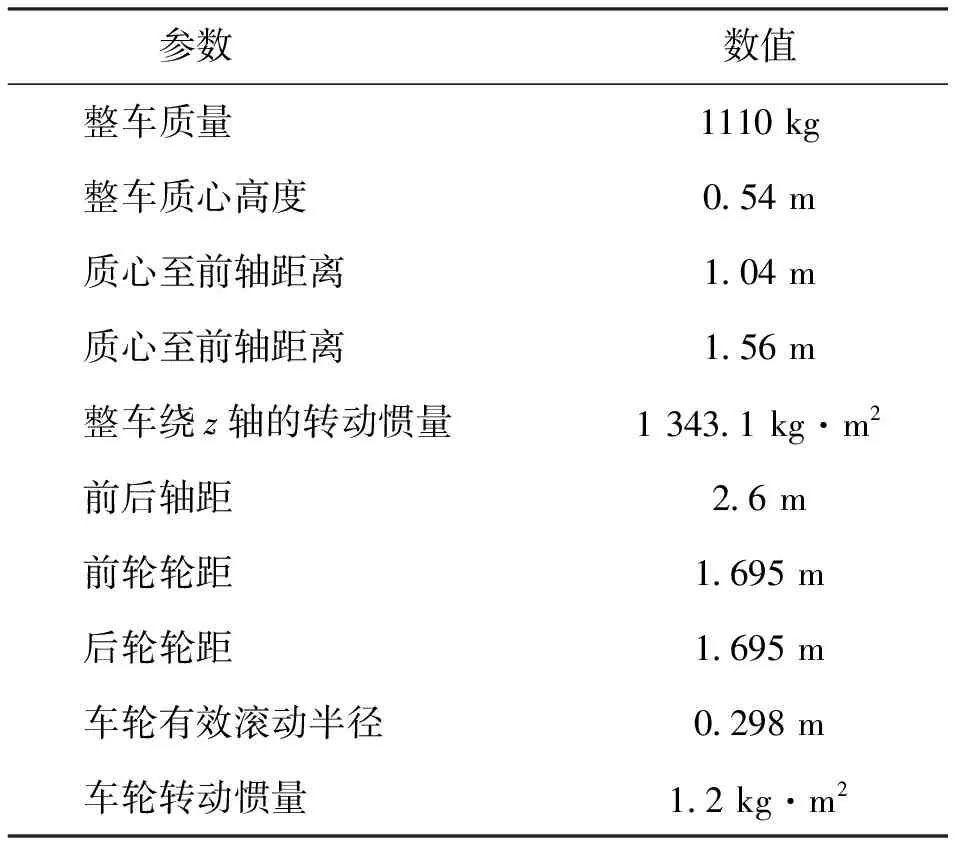
表2 整车动力学模型关键参数

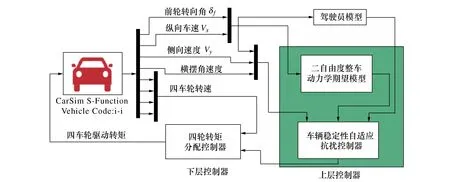
图4 联合仿真原理图

仿真实验工况选用ISO双移线实验工况,试验路面分别选择附着系数为0.35的积雪路面及附着系数为0.46的湿泥土路面,行驶速度分别采用低速及中速两种,如表3所示。

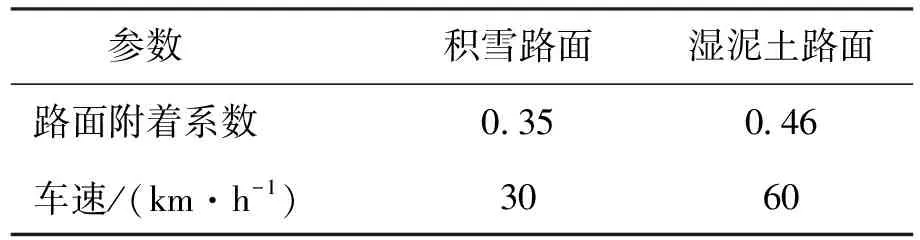
表3 试验工况设置

试验考虑以30 km/h在积雪路面行驶及60 km/h在湿泥土路面行驶工况下,整车自适应抗扰算法控制的横摆稳定性指标跟踪理想值的能力,用以衡量控制系统的实施效果。仿真实验同时考虑CarSim原车未载乘客及重物时整备质量与满载时整车质量进行对比试验分析,验证所设计自适应抗扰算法的控制效果。车辆质量随载人多少而变化,同时整车绕z轴的转动惯量也随质量一同变化,设定两个参数非线性扰动工况如表4所示。

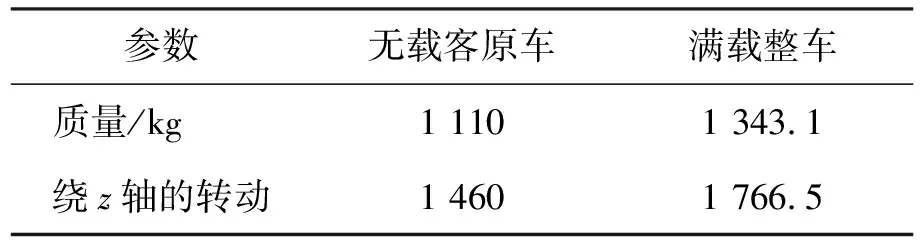
表4 整车参数变动工况

进行双移线工况仿真分析,Carsim整车模型在两种路面行驶的质心侧偏角、横摆角速度对比如图5a)～图5d)所示。图5a)与图5b)为车辆在积雪路面进行仿真试验所得结果。由图5a)仿真结果可知,整车以30 km/h在积雪路面行驶时的理想质心侧偏角变化范围为-2.6°～1.73°。无控制原车空载及满载行驶过程中的质心侧偏角与理想值最大偏离量为53.7%与63%。

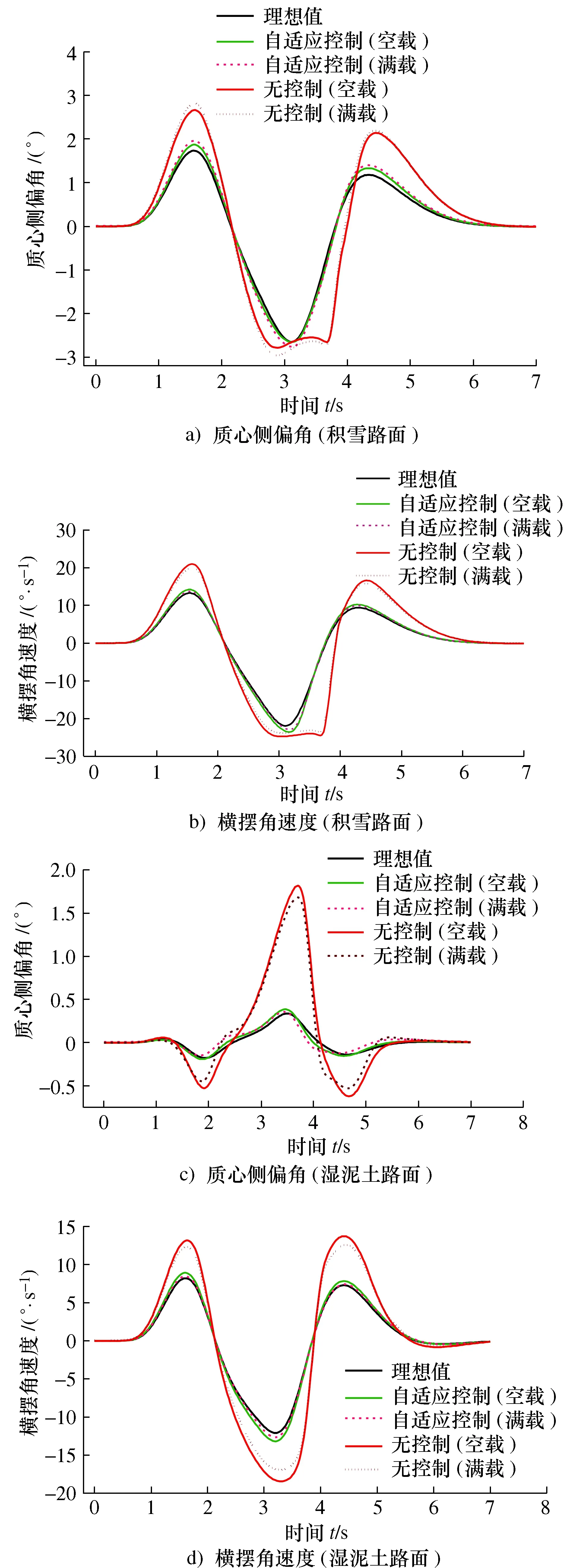
图5 联合仿真试验结果

自适应控制整车空载及满载工况的质心侧偏角与理想值最大偏离量为8%与13.3%。由5b)仿真结果可知,积雪路面行驶工况中整车理想横摆角速度的变化范围为-21.92°/s～13.31°/s。无控制原车空载与满载工况的横摆角速度相对理想值最大偏离程度分别为56%与49%;自适应控制整车空载与满载工况横摆角速度相对理想值最大偏离程度分别为6%与3.3%。仿真结果表明在积雪路面行驶工况中,无控制原车行驶出现了轻度打滑现象,自适应抗扰控制器可使整车质心侧偏角及横摆角速度较准确地跟踪理想值,提升了整车横摆稳定性。图5c)与图5d)为车辆在湿泥土路面进行仿真实验所得结果。由图5c) 仿真结果可知,整车以60 km/h在湿泥土路面行驶时,车辆的理想质心侧偏角变化范围为-0.18°～0.34°。无控制原车空载及满载行驶过程中的质心侧偏角与理想值最大偏离量达376.5%与347.1%。自适应控制整车空载及满载工况的质心侧偏角与理想值最大偏离量为11.7%与22.2%。由图5d)仿真结果可知,车辆在湿泥土路面理想横摆角速度变化范围为-12.1°/s～8.2°/s。无控制原车空载与满载工况的横摆角速度相对理想值最大偏离程度分别为59.8%与49.8%;自适应控制整车空载与满载工况横摆角速度相对理想值最大偏离程度分别为8.7%与3.6%。由于车速较快,无控制原车在湿泥土路面上出现较明显打滑现象,自适应控制器使车辆能较好地保持横向稳定性,提升了整车的安全性能。仿真实验中,整车质量及绕z轴的转动惯量的变化对无控制原车的影响较明显,而自适应抗扰控制器有效抑制参数扰动带来的影响,增强了控制系统的鲁棒性。由联合仿真结果可知,所设计自适应抗扰控制器可使车辆在极限工况下保持良好的转向操纵能力,有效地提升车辆的横摆稳定性,具有较好的自适应性及抗干扰能力。

4 结论

1) 建立四轮毂电机驱动汽车二自由度整车动力学模型,并推导得出二自由度整车动力学期望模型。搭建整车自适应分层控制系统,上层控制器实现自适应跟踪整车动力学理想模型状态变量、计算整车横摆稳定性优化所需附加转矩。下层控制器完成车轮驱动转矩实时优化分配,提升车辆操纵稳定性。

2) 基于线性二次型最优控制及模型参考自适应控制理论,提出一种新的四轮独立驱动电动汽车转矩控制方法。运用线性二次型最优控制器计算出汽车对期望横摆稳定性参数跟踪的控制量。基于李雅普诺夫稳定性理论,提出一种整车横摆稳定性自适应抗扰控制方法。在车辆动力学模型参数扰动情况下,减小控制对象参数变动造成的控制偏差。搭建CarSim与MATLAB/Simulink联合仿真平台,验证四轮驱动EV转矩自适应抗扰控制算法有效性。仿真结果表明,所设计自适应抗扰控制器可有效提升四轮独立驱动EV的横摆稳定性,具有自适应能力强、稳定性好及抗干扰能力强的特点。